Hyvän vastauksen piirteet: FI – Fysiikka
15.9.2021
Lopulliset hyvän vastauksen piirteet 11.11.2021
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
Osa 1: 20 pisteen tehtävä
1. Täydennystehtäviä fysiikan eri osa-alueilta 20 p.
1.1 Täydennä lause 2 p.
- gravitaatio (2 p.)
1.2 Täydennä lause 2 p.
- vahva (2 p.)
1.3 Täydennä lause 2 p.
- kiihtyvässä (2 p.)
1.4 Täydennä lause 2 p.
- liikemäärä (2 p.)
1.5 Täydennä lause 2 p.
- kasvaa (2 p.)
1.6 Täydennä lause 2 p.
- pysyy vakiona (2 p.)
1.7 Täydennä lause 2 p.
- pienenee (2 p.)
1.8 Täydennä lause 2 p.
- taajuus (2 p.)
1.9 Täydennä lause 2 p.
- eri merkkiset (2 p.)
1.10 Täydennä lause 2 p.
- magneettivuon muutos (2 p.)
Myös muut oikeat ilmaisut hyväksytään.
Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
Osa 2: 15 pisteen tehtävät
2. Sulkapallo 15 p.
2.1 Esitä graafisesti sulkapallon mitattu nopeus ajan funktiona. Esitykseen ei tarvitse tehdä graafista tasoitusta. 4 p.
Piirretään mittauspisteistä graafinen esitys. (Kuvaan on piirretty myös kohtaan 2.2 liittyvät suoransovitukset.)
Pisteitys:
- On esitetty kuvaaja, jossa mittaustulokset näkyvät erillisinä mittauspisteinä. 4 p.
- Jos kuvassa on esitetty väärä data tai mittauspisteet eivät näy lainkaan, vähennetään 4 pistettä.
- Jos kaikki datapisteet eivät ole näkyvissä, vähennetään 2 pistettä ja jos datapisteet on esitetty murtoviivalla vähennetään 1 piste.
- Jos asteikon akselit ovat väärin päin, suureen tunnus/tunnuksia puuttuu tai yksikkö/yksiköitä puuttuu, vähennetään kummastakin näistä 1 piste.
Tyypillisiä virheitä: Mittaustulosten esittäminen murtoviivalla tai esitettyjen mittauspisteiden tarpeeton yhdistäminen murtoviivalla.
2.2 Päättele graafisesta esityksestä, millä hetkellä sulkapallo on korkeimmillaan. Millä aikavälillä pallon nopeus on likimain vakio? 4 p.
Aluksi sulkapallo liikkuu ylöspäin ja sen nopeus on positiivinen. Kun pallon nopeus on hetkellisesti nolla, se on saavuttanut lakikorkeuden. Piirretyistä mittauspisteistä voidaan arvioida tämän tapahtuvan kohdassa t = 0,9 s.
Mittauspisteisiin on sovitettu suora välille 0,70 s – 1,15 s. Suora ja sen yhtälö on esitetty kohdan 2.1 kuvassa. Ratkaistaan suoran yhtälöstä aika, jolloin v = 0:
t=\frac{0\,{\rm m/s}-9,\!3079\,{\rm m/s}}{-9,\!9434\,{\rm m/s^2}} = 0,\!9361\,{\rm s} \approx 0,\!94\,{\rm s}.Graafisen esityksen perusteella pallon nopeus pysyy vakiona noin aikavälillä 2,4 s – 2,8 s.
Pisteitys:
- On annettu tulos väliltä 0,90 s ... 0,95 s. 2 p.
- On annettu aikaväli, jossa alkupiste on välillä 2,0 s ... 2,4 s ja loppupiste 2,8 s. 2 p.
Täysiin pisteisiin edellytetään vastauksen antamista kahden merkitsevän numeron tarkkuudella. Jos lopputulokset on annettu suuremmalla tarkkuudella, vähennetään 1 piste kummankin tuloksen pisteistä.
Tyypillinen virhe: Liian suuri tarkkuus.
2.3 Ilmanvastuksen suuruudelle F_D pätee malli F_D = \frac{1}{2} C \rho A v^2, jossa C on kappaleen muodosta riippuva kerroin, \rho on ilman tiheys (1,22 kg/m3), A on kappaleen poikkipinta-ala ja v on kappaleen nopeus. Tarkastele aikaväliä, jolla pallon nopeus on likimain vakio. Määritä kerroin C kokeessa käytetylle sulkapallolle. 7 p.
Newtonin 2. lain perusteella kappaleen kiihtyvyys on nolla, kun siihen vaikuttava kokonaisvoima on nolla. Koska tarkasteltavassa kohdassa nopeus ei muutu, ovat voimat yhtä suuret.
Voimille pätee nyt F_G = F_D eli
mg = \frac{1}{2}C\rho A v^2.Kertoimelle C saadaan suureyhtälö
C = \frac{2mg}{\rho A v^2}Lasketaan pallon nopeuksien itseisarvojen keskiarvo aikavälillä 2,40 s – 2,81 s. Taulukkolaskimella saadaan v = 6,5783 m/s.
Käytetään putoamiskiihtyvyydelle arvoa g = 9,81 m/s2 ja ilman tiheydelle annettua arvoa \rho = 1,22 kg/m3. Saadaan
\begin{eqnarray*} C &=& \frac{2mg}{\rho A v^2} = \frac{2\cdot 0,0048\text{ kg}\cdot9,81\text{ m/s}^2}{0,0030\text{ m}^2\cdot1,22\text{ kg/m$^3$}\cdot(6,5783\text{ m/s})^2} \\&=& 0,5946 \approx 0,59. \end{eqnarray*}Pisteitys:
- On käytetty perusteluna Newtonin II lakia tai voimatasapainoa. 2 p.
- On annettu kysytyn suureen C suhteen ratkaistu suureyhtälö. 2 p.
- On annettu välillä 0,59...0,62 oleva lopputulos yhden tai kahden merkitsevän numeron tarkkuudella. 3 p.
- Jos lopputulos on annettu suuremmalla tarkkuudella, vähennetään 1 piste.
Tyypillisiä virheitä: Perustelu tai kertoimen C suureyhtälö puuttuu.
3. Lämmitysvastuksen teho 15 p.
Graafinen esitys:
Graafisen esityksen pisteitys:
- On esitetty kuvaaja pesuohjelman lämpötilasta (tai lämpötilojen erotuksista) tai veden lämmittämiseen käytetyn energian määrästä pesuohjelman keston funktiona. Mittaustulosten tulee näkyä erillisinä mittauspisteinä. 5 p.
- Jos datapisteet eivät erotu, vähennetään 3 pistettä.
- Jos datapisteet on esitetty murtoviivalla, vähennetään 1 piste.
- Asteikolta puuttuvista suureen tunnuksesta/tunnuksista tai yksiköstä/yksiköistä vähennetään kummastakin 1 piste.
- Jos graafisesta esityksestä puuttuu mittauspisteisiin sovitettu suora, vähennetään 2 pistettä.
Pesuohjelman lämpötilan ja keston riippuvuus nähdään kuvaajasta. Datapisteisiin sovitetun suoran kulmakertoimesta saadaan veden lämpenemisnopeudeksi kaikissa pesuohjelmissa
\frac{\Delta T}{t}= 1,132\ ^{\circ}{\rm C/min} = 0,0189\ ^{\circ} {\rm C / s}.Lämmitettävän veden määrä on puolet kokonaisvedenkulutuksesta:
m= \frac{37 \rm \ l \cdot 1,0 \rm \ kg/l}{2} = 18,5 \rm \ kg.Lämmitysvastuksen tehon lauseke P={E}/{t} ja veteen siirtyvän lämpöenergian lauseke E=cm \Delta T yhdistettynä tuottavat teholle lausekkeen
P= \frac{E}{t}\ =cm \frac{\Delta T}{t}.Tästä saadaan lämmitysvastuksen tehoksi
P=4,\!186 {~\rm kJ / kg}\cdot 18,\!5 {~\rm kg} \cdot 0,\!0189\; ^{\circ} {\rm C/ s}=1,\!464 {~\rm kW} \simeq 1,\!5 {~\rm kW.}Lämmitysvastuksen teho on noin 1,5 kW.
Laskennallisen osan pisteitys:
- On luettu graafisesta esityksestä lämpenemisnopeuden arvo 1.1–1.2 ℃/min (tai 0,018-0,020 ℃/s) tai tehon arvo 1,4–1,5 kW. 3 p.
- On esitetty ja käytetty suureyhtälöä energialle ominaislämpökapasiteetin avulla. 2 p.
- On esitetty tehon suureyhtälö energian avulla ja käytetty sitä. 2 p.
- On annettu välillä 1,4–1,5 kW oleva lopputulos kahden tai kolmen merkitsevän numeron tarkkuudella. 3 p.
- Jos tulos on saatu graafista esitystä käyttämättä vähennetään laskuosuuden pisteistä 6 pistettä.
- Jos ratkaisusta on jäänyt veden määrä jakamatta kahdella, vähennetään 3 pistettä.
4. Ilmapallo 15 p.
4.1 Mitä ilmapallolle tapahtuu, kun sitä hangataan vaatteisiin? 3 p.
Kun ilmapalloa hangataan vaatetta vasten, siihen siirtyy vaatteesta elektroneja tai siitä siirtyy elektroneja vaatteeseen. Ilmapallo tulee tämän hankaussähkön takia sähköisesti varautuneeksi.
Pisteitys:
- On kerrottu, että pallosta vaatteeseen tai vaatteesta palloon siirtyy elektroneja. 2 p.
- On kerrottu, että pallo varautuu sähköisesti 1 p.
Tyypillisiä virheitä: Kuvattu elektronien siirtyminen tai varauksen järjestäytyminen pallon sisällä tai pinnalla. Puhuttu elektronien sijasta varauksista tai hiukkasista.
4.2 Selitä, miksi ilmapallo tarttuu seinään ja pysyy siinä paikallaan. Piirrä selityksesi tueksi kuvaan ilmapalloon vaikuttavien voimien voimavektorit ja nimeä voimat. 8 p.
Kun varautunut ilmapallo viedään seinän läheisyyteen, sen sähkökenttä aiheuttaa seinän pinnan atomeissa ja molekyyleissä sähköisen polarisoitumisen. Tästä aiheutuu ilmapalloon kohtisuorasti seinään päin kohdistuva sähköinen voima \bar F_{\rm s}. Seinä kohdistaa ilmapalloon tukivoiman \bar N, joka on yhtä suuri kuin tämä sähköinen voima. Ilmapallo pysyy paikallaan, kun ylöspäin suuntautuva ilmapallon ja seinän välinen lepokitka \bar F_{\mu} on yhtä suuri kuin alaspäin vaikuttava ilmapallon paino \bar G. Voimat ovat sähköinen voima, pinnan tukivoima, paino ja lepokitka.
Pisteitys:
- On piirretty voimakuvio, jossa näkyy neljä oikeaa voimaa. 2 p.
- Mikäli voimakuviosta puuttuu voima tai siinä on ylimääräisiä voimia, voimakuviosta ei anneta pisteitä. Mikäli voimakuviossa esitettyjen voimanuolien pituudet eivät ole oikeassa suhteessa toisiinsa, vähennetään 1 piste.
- On nimetty kaikki neljä vaadittua voimaa. 2 p.
- Mikäli korkeintaan kaksi nimeämistä on väärin tai puuttuu, vähennetään 1 piste.
- Selityksessä on mainittu polarisoituminen tai sähköinen voima. 2 p.
- On todettu kitkan merkitys. 2 p.
Tyypillisiä virheitä: Kuvattu sähköisen voiman syntyminen ikäänkuin myös seinä olisi varautunut. Otettu tarkasteluun mukaan palloon kohdistuvien voimien vastavoimia. Jätetty kitka huomioimatta.
4.3 Miksi ilmapallo alkaa jonkin ajan kuluttua laskeutua seinää pitkin alas? 4 p.
Ilmapallon sähkövaraus pienenee aikaa myöten, koska ilmapallon ja seinän välille syntyy sähkövirta. Kun ilmapallon sähkövaraus pienenee, pienenevät myös seinän ilmapalloon kohdistamat sähköinen voima \bar F_{\rm s} ja pinnan tukivoima \bar N. Tukivoiman pieneneminen pienentää lepokitkaa ilmapallon ja seinän välillä. Kun varaus on pienentynyt riittävästi, lepokitkan suurin arvo tulee pienemmäksi kuin ilmapalloon kohdistuva paino eli \mu_0 N<G. Silloin ilmapallo joutuu alaspäin suuntautuvaan kiihtyvään liikkeeseen.
Pisteitys:
- On mainittu ilmapallon varauksen pieneneminen. 2 p.
- Kuvattu miten tukivoiman pieneneminen vaikuttaa kitkaan. 2 p.
Tyypillinen virhe: Puhutaan varauksien tai varauseron tasoittumisesta pallon ja seinän välillä.
5. Keinu 15 p.
Keinuun vaikuttavat voimat ovat keinun ja keinujan yhteenlaskettu paino \overline G = m\overline g ja narujen yhteenlaskettu jännitysvoima \overline T.
Keinun liike on ympyräliikettä, joten radan normaalin suunnassa on voimassa yhtälö
ma_{\rm n}=T - G_{\rm n},jossa G_{\rm n} on painon komponentti radan normaalin suunnassa.
Jännitysvoimalle saadaan yhtälö
T=ma_{\rm n} + G_{\rm n}.Jännitysvoimaan vaikuttavista tekijöistä G_{\rm n} on suurimmillaan, kun keinu on ala-asemassa, jolloin G_{\rm n} = G. Myös kiihtyvyys a_{\rm n}=v^2/r on suurin ala-asemassa, koska nopeus on silloin energiaperiaatteen mukaisesti suurimmillaan. Naruihin kohdistuva kuormitus on siis suurin ala-asemassa.
Mekaanisen energian säilymisen nojalla potentiaalienergian ja liike-energian summa E_{\rm p}+E_{\rm k} on vakio, joten
\frac{1}{2}m v^2 =mgh,josta saadaan keinun maksiminopeuden neliöksi
v^2=2gh.Jännitysvoima ala-asemassa on
T=\frac{2mgh}{r}+mg=3mg,koska h = r.
Narujen jännityksen suurin arvo on
T_{\rm max}=3mg.Jotta narut eivät katkeaisi, arvon tulee olla pienempi kuin annettua murtolujuutta vastaavan voiman. Koska voima jakautuu kahteen naruun, saadaan yhtälö
T_{\rm max}<2m_{\rm murtolujuus} geli
m<\frac{2m_{\rm murtolujuus}}{3}=\frac{2\cdot 65 \;{\rm kg} }{3}\simeq 43\; {\rm kg.}Pisteitys:
- On esitetty oikeat voimat sisältävä voimakuvio jostain heilahduksen vaiheesta. 2 p.
- On esitetty voimille suureyhtälö normaalin suunnassa tai heilahduksen alimmassa kohdassa. 2 p.
- On todettu, että narujen jännitys on suurin keinun ollessa pystysuorassa. 2 p.
- On perusteltu oikein, miksi jännitys on suurin narun ollessa pystysuorassa. 2 p.
- Keinun keskeiskiihtyvyys on huomioitu. 2 p.
- Mekaanisen energian säilymistä on käytetty ratkaisussa. 2 p.
- On annettu (yhden tai kahden) narun jännitysvoiman suureyhtälö tai jännitysvoiman suuruus. 1 p.
- On annettu lopputulos kahden merkitsevän numeron tarkkuudella. 2 p.
Tyypillinen virhe: On laskettu murtolujuus keskeiskiihtyvyyttä huomioimatta ja annettu vastauksena joko 65 kg tai 130 kg.
6. Huilu ja klarinetti 15 p.
6.1 Määritä perussävelen taajuus sekä vastaava aallonpituus. 5 p.
Sekä spektrissä A että spektrissä B taajuudeltaan pienin ja amplitudiltaan suurin piikki on (noin) 264 hertsin kohdalla. Perussävelen taajuus on siis f = 264\ {\rm Hz\ (260...270\ Hz)}.
Vastaava aallonpituus saadaan aaltoliikkeen perusyhtälöstä:
\lambda=\frac{v}{f}=\frac{343\,{\rm m/s}}{264\,{\rm Hz}}\approx 1{\rm ,}3\,{\rm m}.Pisteitys:
- Luettu oikea taajuus 260...270 Hz spektreistä. 2 p.
- On esitetty aallonpituuden suureyhtälö ja arvo kahden tai kolmen merkitsevän numeron tarkkuudella. 3 p.
- Jos vastaus on annettu suuremmalla tarkkuudella, vähennetään 1 piste.
6.2 Selvitä fysikaalisesti perustellen, esittääkö kuvan spektri A huilulla vai klarinetilla soitetun sävelen spektriä. 10 p.
Riittää, että kokelas käsittelee vain jommankumman tapauksen (huilu tai klarinetti) ja valitsee oikean vastauksen tämän perusteella. Alla käsitellään molemmat tapaukset.
Spektreissä A ja B näkyy perustaajuuden monikertoja. Spektrissä A ne ovat 792 Hz ja 1 320 Hz ja spektrissä B 528 Hz, 792 Hz, 1 056 Hz.
Huilu on molemmista päistä avoin putki, jolloin kaikkia säveliä (perussävel ja yläsävelet) vastaavat ääniaallon kuvut (paineminimit) putken molemmissa päissä. Klarinetti on toisesta päästä avoin ja toisesta suljettu putki, jolloin kaikkia säveliä (perussävel ja yläsävelet) vastaavat ääniaallon solmukohta (painemaksimi) putken suljetussa päässä ja kupu (paineminimi) putken avoimessa päässä. (Tarkastelua voi täydentää kuvalla.)
Jos huilun perussävelen aallonpituus on \lambda_1, niin yläsävelten aallonpituudet ovat \lambda_2=\lambda_1/2,\; \lambda_3=\lambda_1/3,\ldots eli \lambda_n=\lambda_1/n, jossa n = 2, 3, . . . Tällöin yläsävelten taajuudet muodostuvat perussävelen taajuuden monikerroista 2f_1,\,3f_1,\,4f_1,\ldots eli f_n=nf_1, jossa n=2,3,\ldots
Jos klarinetin perussävelen aallonpituus on \lambda_1, niin yläsävelten aallonpituudet ovat \lambda_2=\lambda_1/3,\; \lambda_3=\lambda_1/5,\ldots eli \lambda_n=\lambda_1/n, jossa n=3,5,\ldots Tällöin yläsävelten taajuudet muodostuvat perussävelen taajuuden parittomista monikerroista 3f_1,\,5f_1,\,7f_1,\ldots eli f_n=nf_1, jossa n=3,5,\ldots
Spektrin B perustaajuuden monikerrat vastaavat huilun tapausta ja spektrin A monikerrat klarinetin tapausta. Spektri A esittää siis klarinetin spektriä.
Pisteitys:
- On luettu ainakin toisesta kuvasta oikeat äänen taajuudet. 2 p.
- On kerrottu, että huilussa syntyy molempiin päihin kupu tai klarinetissa toiseen päähän kupu ja toiseen päähän solmu. 3 p.
- On selvitetty aallonpituuksien avulla ainakin toisen soittimen äänen taajuudet. 3 p.
- On kerrottu, että spektri A on klarinetin spektri. 2 p.
7. Sähkömoottori 15 p.
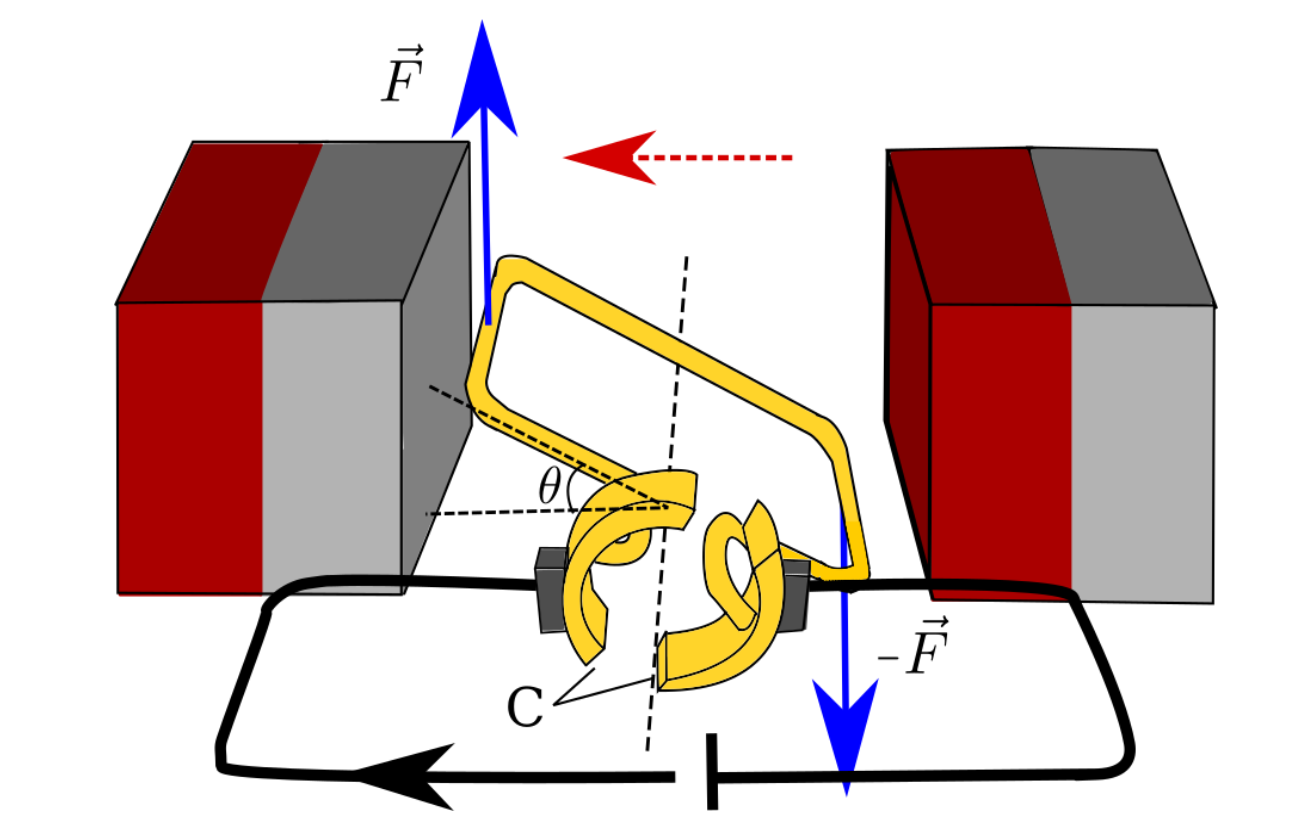
7.1 Piirrä kuvaan niiden voimien voimavektorit, jotka pyörittävät silmukkaa. 4 p.
Voimien suunnat ovat kohtisuorassa sekä magneettikenttää että sähkövirtaa vastaan (kuvassa alas ja ylös), ja voimat ovat yhtä pitkiä.
Pisteitys:
- On piirretty molemmat voimavektorit oikeisiin paikkoihin oikean suuntaisina. 4 p.
- Mikäli molemmat voimat ovat 180° väärään suuntaan tai on piirretty vain yksi oikeaan suuntaan osoittava voima, vähennetään 2 pistettä.
7.2 Johda lauseke silmukkaan kohdistuvan momentin M suuruudelle kiertokulman θ funktiona. Mikä on momentin suurin arvo? 8 p.
Magneettikentän suuntaa vastaan kohtisuoriin johtimiin kohdistuvat voimat pyörittävät silmukkaa. Yhteen johtimeen kohdistuvan voiman suuruus on
F=IlB,ja kokonaismomentin suuruus on kumpaankin johtimeen kohdistuvien voimien ja niiden momenttivarsien tulojen summa
\Sigma M=Fa+Fa.Momenttivarren pituus a=l/2\cos\theta, jossa \theta on kiertokulma ja l silmukan sivun pituus. Tällöin kokonaismomentin suuruus on siis
\Sigma M=Il^2 B\cos\theta.Momentin suurin arvo saadaan kun a=l/2, M=Il^{2}B = 6{,}6\muNm.
Pisteitys:
- On annettu yhteen johtimeen kohdistuvan voiman suureyhtälö. 2 p.
- On annettu momentin suureyhtälö voiman avulla esitettynä. 2 p.
- On annettu momentin suureyhtälö kulman θ funktiona. 2 p.
- On annettu lopputulos kahden tai kolmen merkitsevän numeron tarkkuudella. 2 p.
- Jos lopputulos on annettu suuremmalla tarkkuudella, vähennetään 1 piste.
Tyypillisiä virheitä:
- Ratkaistu tehtävä taulukkokirjasta löytyvällä momentin kaavalla M = NIA\sin(\alpha). Tällöin ratkaisusta voi saada korkeintaan 4 pistettä (edellyttäen, että kulma on käsitelty oikein).
- Lähdetty voiman suureyhtälöstä F = I \ell B \sin(\alpha) olettamalla, että \theta = \alpha.
7.3 Moottorin silmukassa on kommutaattori (merkintä C kuvassa ), joka kääntää silmukassa olevan virran suunnan. Miksi tämä on moottorin toiminnan kannalta tärkeää? 3 p.
Johtimeen kohdistuva voima riippuu vain virran ja magneettikentän suunnista, ei johtimen paikasta magneettikentässä. Jotta moottori pyörisi, voiman suunnan pitää muuttua, kun johdin kulkee silmukan akselin ylitse tai alitse. Kommutaattori saa tämän aikaan.
Pisteitys:
- On kuvattu oikein pyörimisen jatkuminen. 3 p.
8. Fuusio 15 p.
8.1 Selitä fuusioreaktorin toimintaperiaate. 9 p.
Fuusiossa kaksi kevyttä atomiydintä yhtyy raskaammaksi ytimeksi vapauttaen samalla energiaa. Vapautuneella energialla tuotetaan vesihöyryä, joka pyörittää sähkögeneraattoria. Fuusioreaktoreissa käytetään vedyn raskaita isotooppeja, deuteriumia ja tritiumia.
Fuusio on vaikea saada aikaan, koska positiivisesti varautuneet atomiytimet hylkivät toisiaan sähköisen vuorovaikutuksen takia. Jotta ytimet saataisiin riittävän lähelle toisiaan, täytyy vedyn isotoopit kuumentaa hyvin korkeaan lämpötilaan, jolloin niistä muodostuu plasmaa. Plasma pidetään koossa magneettikenttien tai lasersäteilyn avulla, jotka estävät plasmaa törmäämästä reaktorin seiniin.
Pisteitys:
- On kerrottu, että kaksi kevyttä ydintä muodostaa yhden raskaamman ytimen ja että reaktiossa vapautuu energiaa. 4 p.
- Mikäli energian vapautuminen puuttuu, vähennetään 2 pistettä.
- On mainittu ytimien välinen hylkivä voima ja siitä johtuva tarve korkealle lämpötilalle. 3 p.
- On mainittu, että plasman koossa pitämiseen tarvitaan magneettikenttä. 2 p.
Tyypillisiä virheitä:
- On väitetty, että fuusiossa yhdistyvät tosiinsa atomit tai hiukkaset.
- On väitetty, että magneettikenttä synnyttää korkean lämpötilan.
8.2
Oletetaan, että tulevaisuudessa fuusioenergialla voidaan korvata laajamittaisesti fissioenergia. Pohdi perustellen, koskevatko seuraavat fissiovoimaloista esitetyt väittämät myös fuusiovoimaloita.
- Voimalalle sopivan sijoituspaikan löytäminen on vaikeaa.
- Voimalan synnyttämän jätteen sijoittaminen on ongelmallista.
- Joillekin valtioille reaktorin hankkiminen on poliittisesti vaikeaa niiden kansainvälisten suhteiden takia.
6 p.
- a) Fuusioreaktorissa ei voi syntyä hallitsematonta ketjurektiota eikä reaktorin sydän jäähdytysjärjestelmän pettäessä voi sulaa. Tämä sallisi voimalan vapaamman sijoittamisen.
- b) Fuusioreaktorin käyttämän tritiumin aktiivisuus on hyvin korkea ja kaasumaisena aineena se leviää tehokkaasti reaktorista riittävän vakavan onnettomuuden seurauksena. Tämän takia reaktoria ei voi sijoittaa sen vapaammin kuin fissioreaktoreitakaan.
- a) Molemmista reaktoreista syntyy rakennemateriaalien altistumisen seurauksena lyhytikäistä (alle 30000 vuotta) radioaktiivista jätettä, ja sen varastointi on samankaltaista kuin fuusioreaktorin lyhytikäisen jätteen.
- b) Fuusioreaktorissa ei synny (hyvin suuren puoliintumisajan) radioaktiivista jätettä, joten jätteen sijoittaminen on yksinkertaisempaa.
- a) Fuusioreaktori ei käytä fissiokelpoista materiaalia, joten sen avulla ei voi suoraan rakentaa ydinasetta. Tämän takia sen hankkimista ei kansainvälisessä politiikassa pyrittäisi samalla tavalla estämään.
- b) Molemmissa reaktoreissa syntyviä neutroneita voidaan käyttää ydinräjähteiden tuottamiseen, joten fuusioreaktoreihin tullaan liittämään samanlaiset kansainväliset rajoitukset.
Pisteitys:
Yksi oikea perustelu joko puolesta tai vastaan (a tai b) jokaiseen väitteeseen ja siihen liittyvä oikea johtopäätös. Kustakin kohdasta 2 p.
Tyypillinen virhe: Vastausta ei ole perusteltu fysiikan argumentteja käyttäen.
Osa 3: 20 pisteen tehtävät
9. Keittolevyt 20 p.
9.1 Kuvaile pääpiirteissään, miten vertailet keittolevyjen energiatehokkuutta. Mitä ja miten mittaat tai määrität? Erittele mitä tekijöitä tulee ottaa huomioon, jotta tulokset olisivat mahdollisimman luotettavia. 10 p.
Kummallakin liedellä lämmitetään vettä ja mitataan kuinka nopeasti vesi lämpenee suhteessa käytettyyn sähkötehoon. Mitattavat asiat ovat veden lämpötila sekä keittolevyn ottama sähköteho tai sähköenergia. Sähköenergian voi mitata kWh-mittarilla ja sähkötehon joko tehomittarilla tai mittaamalla virran ja jännitteen.
Mittauksissa tulee vakioida (tai kontrolloida) kokeen alkutila, johon kuuluvat ainakin veden määrä sekä veden, lämmitysastian ja lieden alkulämpötila. Ulkoisten olosuhteiden tulee myös olla vastaavat kaikissa mittauksissa, ja kokeissa täytyy käyttää samaa tai samanlaista kattilaa.
Pisteytys:
- On kuvattu veden lämpötilan mittaaminen ajan funktiona lämmittämisen aikana tai veden kiehuvaksi lämmittämiseen kuluvan ajan mittaaminen. 2 p.
- On kuvattu energian mittaus kWh-mittarilla, tehon mittaaminen tehomittarilla tai sähkövirran mittaus jännite mainiten. 3 p.
- On kerrottu, että veden määrä ja alkulämpötila pitää mitata. 3 p.
- On kerrottu, että tulee käyttää samanlaista/samaa kattilaa ja samaa kattilan alkulämpötilaa. 2 p.
9.2 Hahmottele graafinen esitys siitä, millaista mittausdataa oletat mittauksista saatavan. Halutessasi voit käyttää tulosten esittämisen apuna aineiston piirrospohjaa. 6 p.
Induktiokeittolevyllä veden lämpötila alkaa nousta nopeammin ja nousu on koko ajan nopeampaa kuin valurautakeittolevyllä. Siten induktiokeittolevyllä saavutetaan veden kiehumispiste (tai muu haluttu loppulämpötila) nopeammin kuin valurautaisella keittolevyllä.
Pisteitys:
- On esitetty graafinen esitys ajatellusta lämpötilasta ajan funktiona. Esityksessä tulee näkyä kaksi oikein nimettyä käyrää ja nimetyt akselit. 2 p. Näitä pisteitä ei anneta, jos lämpötilan nousu tapahtuu samalla kulmakertoimella molemmille liesille tai lämpeneminen kiihtyy ajan edetessä.
- Kuvasta käy ilmi, että käyrät lähtevät nousemaan alkulämpötilasta eri hetkellä ja/tai eri kulmakertoimella. 2 p.
- Kuvasta käy ilmi, että käyrät saavuttavat saman loppulämpötilan eri aikaan tai eri lämpötila samassa ajassa 2 p.
9.3 Tutkimuksessa osoittautuu, että toinen keittolevyistä on energiatehokkaampi. Mistä fysikaalisista syistä ero energiatehokkuudessa johtuu? 4 p.
Induktiokeittolevy on energiatehokkaampi. Se lämmittää suoraan keittoastiaa eikä suurta rautakappaletta, kuten valurautainen keittolevy, joten lämmitettävien kappaleiden (keittolevy + kattila + vesi) kokonaislämpökapasiteetti on pienempi. Induktiokeittolevyn keraaminen pinta on huono lämmönjohde, joten kattilasta siirtyy siihen vain vähän lämpöenergiaa. Induktiokeittolevy ei myöskään lämpene veden kiehumispistettä kuumemmaksi. Valurautalevyn sen sijaan tulee olla huomattavasti yli 100-asteinen, jotta lämpöä siirtyisi keittoastiaan riittävän nopeasti. Mitä viileämpänä keittolevy pysyy vettä keitettäessä, sitä vähemmän siitä säteilee ja johtuu energiaa hukkaan ympäristöön.
Pisteitys:
- Vastauksesta käy ilmi, että induktioliesi ei lämpene. 2 p.
- Todettu, että induktioliedestä siirtyy sen alemman lämpötilan takia vähemmän energiaa ympäristöön kuin valurautaliedestä. 1 p.
- Todettu, että induktioliedestä siirtyy vähemmän energiaa ympäristöön sen pienemmän lämmönjohtavuuden takia. 1 p.
10. Radiometrinen mittaus 20 p.
10.1 Kirjoita hajoamisyhtälö isotoopin Am-241 alfahajoamiselle ja selitä lyhyesti, mistä gammakvantti syntyy. 4 p.
Hajoamisen yhteydessä syntyy virittynyt Np-237 -ydin. Viritystilan purkautuessa ydin emittoi gammakvantin.
Pisteitys:
- On annettu oikea hajoamisyhtälö 2 p.
- On kerrottu gammakvantin syntyvän ytimen viritystilan purkautuessa. 2 p.
Tyypillinen virhe: Kerrotaan säteilyn syntyvän atomin viritystilan purkautuessa.
10.2 Osoita, että nesteen ja kaasun absorptiokertoimien erotukselle \Delta \mu=\mu_1-\mu_2 pätee yhtälö \Delta\mu= \displaystyle{\frac{1}{x}}\ln\left(\displaystyle{\frac{I_2}{I_1}}\right). 4 p.
Käytetään absorptiolakia I=I_0 e^{-\mu x}. Kokonaisintensiteetti silloin, kun putkessa on ainoastaan nestettä, on I_1=I_0 e^{-\mu_1 x}. Kokonaisintensiteetti silloin, kun putkessa on ainoastaan kaasua, on I_2=I_0 e^{-\mu_2 x}. Näistä saadaan
\ln\left(\frac{I_1}{I_0}\right) =\ln I_1 -\ln I_0 =-\mu_1 x,\\ \ln\left(\frac{I_2}{I_0}\right) =\ln I_2 -\ln I_0 =-\mu_2 x.Yhtälöiden erotuksesta saadaan puolestaan
\ln I_2-\ln I_1 =\ln\left(\frac{I_2}{I_1}\right)=\mu_1 x -\mu_2 x =x(\mu_1-\mu_2) = x\Delta\mu.Jakamalla keskimääräisellä paksuudella saadaan
\Delta\mu= \frac{1}{x} \ln\left(\frac{I_2}{I_1}\right)\!,jolloin voidaan todeta, että tehtävässä absorptiokertoimien erotukselle annettu yhtälö pätee.
Pisteitys:
- On annettu intensiteetit I1 ja I2 absorptiolain avulla 2 p. ja johdettu oikein pyydetty suureyhtälö. 2 p.
Tyypillinen virhe: Käytetty lähtökohtana heikennyslakia muodossa I_2=I_1 e^{-\Delta\mu x}
10.3 Neste-kaasuseokselle voidaan esittää niin sanottu efektiivinen absorptiokerroin \mu=\mu_1-\alpha(\mu_1-\mu_2), jossa \alpha on kaasun suhteellinen osuus neste-kaasuseoksen tilavuudesta. Oleta, että virtausnopeus on vakio ja että mittausarvot on saatu tasaisin aikavälein. Putken geometria ei vaikuta intensiteettimittauksiin. Määritä prosentteina kaasun keskimääräinen osuus putkessa virtaavasta materiaalista koko mittauksen aikana (kuva ja mittausaineisto ). Anna vastaus kolmen merkitsevän numeron tarkkuudella. 8 p.
Lähtökohdat: \mu=\mu_1 -\alpha(\mu_1 -\mu_2) ja kohdassa 10.2 saatu \Delta\mu:n lauseke. Ero mittauksien aikana mitatun maksimiabsorptiokertoimen ja putkessa virtaavan materiaalin hetkellisen efektiivisen absorptiokertoimen välillä voidaan laskea käyttäen hetkellistä intensiteettiä ja mittauksien aikana mitattua minimi-intensiteettiä. Kun käytetään edellisestä osatehtävästä absorptiokertoimien erotukselle johdettua yhtälöä, saadaan
(\mu_1-\mu)=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!.Sijoittamalla tähän tehtävässä annettu efektiivisen absorptiokertoimen lauseke
\mu=\mu_1-\alpha(\mu_1-\mu_2)saadaan (\mu_1-\mu)= \mu_1-[\mu_1-\alpha(\mu_1-\mu_2)]=\alpha(\mu_1 -\mu_2)=\alpha\Delta \mu , joten
\alpha\Delta \mu=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!.Käyttämällä kohdassa 10.2 saatua \Delta\mu:n lauseketta, saadaan tästä yhtälö
\frac{\alpha}{x}\ln\left(\frac{I_2}{I_1}\right)=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!eli
\alpha= \frac{\ln\left(I/I_1\right)}{\ln\left(I_2/I_1\right)}.Jokaiselle mitatulle hetkellisen intensiteetin arvolle I_i voidaan laskea vastaava kaasun suhteellinen osuus kokonaisainemäärästä \alpha_i. Virtausnopeus ja mittausaikaväli ovat vakioita, joten kaasun suhteellinen osuus kokonaisainemäärästä koko mittauksen aikana on kaikkien \alpha_i-arvojen keskiarvo eli
\alpha_{\rm ka}=\frac{1}{N}\sum\alpha_i =\frac{1}{N}\sum \frac{\ln\left(\displaystyle{\frac{I_i}{I_1}}\right)}{\ln\left(\displaystyle{\frac{I_2}{I_1}}\right)}.Taulukko-ohjelman avulla voidaan arvioida intensiteettien maksimi- ja minimiarvot. Minimi-intensiteetti voidaan arvioida laskemalla intensiteetin keskiarvo aikavälillä 1 870 ms – 2 030 ms:
I_1=37,\!992251\, {\rm cpms}\approx 38\ {\rm cpms}\, (\pm 1\, {\rm cpms}).Maksimi-intensiteetti voidaan arvioida laskemalla intensiteetin keskiarvo aikavälillä 1 440 ms – 1 710 ms:
I_2=50,\!340521\, {\rm cpms}\approx 50 {\rm cpms}\, (\pm 1 \, {\rm cpms}).Näin saadaan kaasun keskimääräiseksi suhteelliseksi osuudeksi
\alpha_{\rm ka} =0,\!378235\approx 38 \% \,(\pm 1 \%).Pisteitys:
- On esitetty ajatus vertailusta hetkellisen intensiteetin ja maksimi/minimi-intensiteettien välillä. 2 p.
- On määritetty intensiteetin maksimi ja minimiarvot. 2 p.
- On johdettu loppulauseke α:lle. 2 p.
- On laskettu oikea lopputulos 2-3 merkitsevän numeron tarkkuudella. 2 p.
- Mikäli tulos on annettu suuremmalla tarkkuudella, vähennetään 1 piste.
10.4 Kuinka paljon maksimi-intensiteetin ja minimi-intensiteetin välinen erotus \Delta I_0=I_1-I_2 muuttuu kymmenessä vuodessa? 4 p.
Hajoamislaki: I=I_0 e^{\displaystyle{{-\lambda t}}}, jossa \lambda =\displaystyle{\frac{\ln 2}{T_{1/2}}} ja T_{1/2}=432,\!2 vuotta.
Intensiteettierotus \Delta I_0=I_2-I_1 =50,\!340521\; {\rm cpms}-37,\!992251\;{\rm cpms}=12,\!348270 \;{\rm cpms}.
Intensiteettiero on
\Delta I_{10}=\Delta I_0e^{\displaystyle{t {\ln 2}/{T_{1/2}}}}=12,\!348270\, {~\rm cpms}\cdot e^{\displaystyle{({\ln 2}/{432,\!2\, {\rm a}}})10 {\rm a}}=12,\!151812\, {~\rm cpms}.\Delta I_{0}-\Delta I_{10}=12,\!348270\, {\rm cpms}-12,\!151812\, {\rm cpms}=0,\!196458\, {\rm cpms}\approx 0,\!20\, {\rm cpms} (\pm {\rm 0,02 cpms)}.
Pisteitys:
- On käytetty hajoamislakia niin, että λ:lla on oikea yksikkö. 2 p.
- On annettu lopputulos 1-3 merkitsevän numeron tarkkuudella. 2 p.
- Jos on käytetty suurempaa tarkkuutta, vähennetään 1 piste.
11. Gravitaatiokentän voimakkuuden mittaaminen 20 p.
11.1 Miksi ja miten maapallon paikalliset massanmuutokset vaikuttavat satelliitin liikkeeseen? Miksi satelliitteja tarvitaan kaksi? 4 p.
Alueilla, joihin on keskittynyt paljon massaa, satelliitteihin kohdistuu suurempi gravitaatiovoima kuin muualla. Kun satelliitti lähestyy tällaista aluetta, sen nopeus kasvaa, ja kun se poistuu sieltä, sen vauhti puolestaan pienenee.
Satelliitteja tarvitaan kaksi, sillä satelliittien vauhdin muutokset päätellään satelliittien välisen etäisyyden muutoksista.
Pisteitys:
- On esitetty ajatusketju: suurempi massa aiheuttaa suuremman gravitaatiovoiman, joka edelleen aiheuttaa suuremman nopeuden. 2 p.
- On kerrottu, että nopeuden muutokset saadaan määritettyä satelliittien välistä etäisyyttä mittaamalla. 2 p.
11.2 Miksi esimerkiksi vuoristot ja muut maanpinnan muodot eivät näy aineiston kuvissa? 3 p.
Kuvaajassa on esitetty gravitaatiokentän voimakkuuden muutos verrattuna kolmen vuoden ajalta keskiarvoistettuun kentän voimakkuuteen. Vuoret ja muut maastonmuodot ovat tällä aikaskaalalla muuttumattomia, joten ne eivät näy kuvaajassa.
Pisteitys:
- Käy ilmi, että mittauksissa käytetään vertailukohtana pitkän ajan keskiarvoa ja että mitattavien muutosten aikaskaala on lyhyempi kuin maanpinnan muotojen muutosten aikaskaala. 3 p.
11.3 Kuinka suuren suhteellisen muutoksen satelliitin putoamiskiihtyvyydessä GRACE-järjestelmä pystyy aineiston mukaan havaitsemaan? 8 p.
Aineistossa kerrottiin, että järjestelmä pystyy havaitsemaan halkaisijaltaan d=300 km ja paksuudeltaan PUUTTUVA cm vesimassan vaikutuksen gravitaatiokentän voimakkuuteen. Tämän kiekon massa on
M=\frac{\pi d^2}{4}h\rho \approx 7 \cdot 10^{11} \rm{kg},jossa \rho on veden tiheys. Vesimassa ei ole pistemäinen, mutta arvioidaan silti sen aiheuttamaa gravitaatiovoimaa yhtälöllä
F=\gamma \frac{mM}{r^2},jossa \gamma on Newtonin gravitaatiovakio, m satelliitin massa ja r satelliitin kiertokorkeus.
Vesimassan aiheuttama putoamiskiihtyvyyden muutos on Newtonin 2. lain perusteella
\Delta a=\frac{F}{m}=\gamma\frac{M}{r^2} \approx 1,88\times 10^{-10} \rm{m/s^2}.Putoamiskiihtyvyyden suhteellinen muutos verrattuna maapallon aiheuttamaan putoamiskiihtyvyyteen on
\frac{\Delta a}{g}=\gamma\frac{M}{gr^2}=\gamma\frac{\displaystyle{\frac{\pi d^2}{4}}h\rho}{gr^2}\approx 2\times 10^{-11}.Pisteitys:
- On esitetty vesikiekon massan suureyhtälö joko erikseen tai osana lopullista suureyhtälöä. 2 p.
- On käytetty gravitaatiovoiman lauseketta ratkaisun kannalta oleellisen asian määrittämiseen. 2 p.
- On annettu suhteellisen muutoksen lauseke. 2 p.
- On annettu lopputulos 1-2 merkitsevän numeron tarkkuudella. 2 p.
- Jos on käytetty suurempaa tarkkuutta, vähennetään 1 piste.
11.4 Mitä sellaista tietoa gravitaatiokentän mittauksella saadaan, jota on vaikea saada muilla mittaustavoilla? 5 p.
Gravitaatiokentän muutokset ovat massan aiheuttamia, joten gravitaatiokentän mittauksella saadaan määritettyä maapallon massajakaumaa. Massan siirtymät liittyvät voimakkaiden maanjäristysten ohella erityisesti veden ja jään siirtymiin. Muilla tavoin on vaikea mitata sellaisia veden ja jään siirtymiä, jotka ovat näkymättömiä. Sellaisia ovat esimerkiksi maanalaiset vesivarastot tai laajalle alueelle jakautuneet vesi- tai jäämäärät.
Pisteitys:
- On tunnistettu Maapallon massan jakautumisen muutosten mittaus. 3 p.
- On mainittu veden tai jään määrien muutosten mittaus tai vulkaaniseen toimintaan liittyvät massojen siirtymät. 2 p.
- Jos vastauksesta ei käy ilmi, että mitataan massojen tai massajakautumien lyhytaikaisia muutoksia, vähennetään 2 pistettä.