Beskrivningar av goda svar: SV – Fysik
15.9.2021
Slutgiltiga beskrivningar av goda svar 11.11.2021
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl färmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms ̈även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer ̈är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
Del 1: 20-poängsuppgift
1. Ifyllnadsuppgifter från fysikens olika delområden 20 p.
1.1 Komplettera meningen 2 p.
- gravitation (2 p.)
1.2 Komplettera meningen 2 p.
- stark (2 p.)
1.3 Komplettera meningen 2 p.
- accelererande (2 p.)
1.4 Komplettera meningen 2 p.
- rörelsemängd (2 p.)
1.5 Komplettera meningen 2 p.
- öka (2 p.)
1.6 Komplettera meningen 2 p.
- förbli konstant (2 p.)
1.7 Komplettera meningen 2 p.
- minska (2 p.)
1.8 Komplettera meningen 2 p.
- frekvens (2 p.)
1.9 Komplettera meningen 2 p.
- har motsatta förtecken (2 p.)
1.10 Komplettera meningen 2 p.
- en förändring i det magnetiska flödet (2 p.)
Även andra korrekta uttryck godkänns.
Rätt svar 2 p., fel svar 0 p., inget svar 0 p.
Del 2: 15-poängsuppgifter
2. En badmintonboll 15 p.
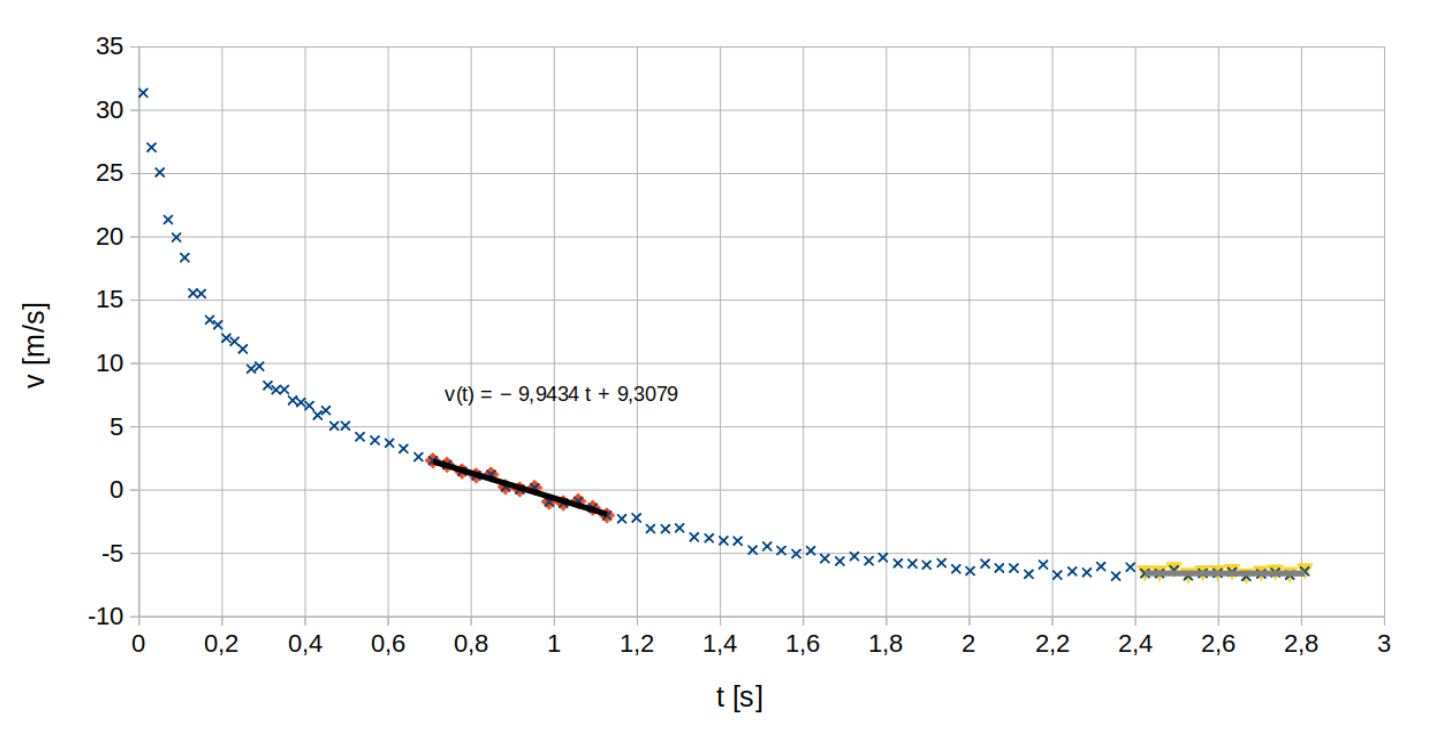
2.1 Presentera grafiskt badmintonbollens uppmätta hastighet som funktion av tiden. En grafisk utjämning behöver inte inkluderas. 4 p.
Vi ritar en grafisk presentation av mätpunkterna. (Även de linjära anpassningarna för deluppgift 2.2 är inritade på bilden.)
Poängsättning:
- Det har presenterats en graf där mätresultaten syns som enskilda mätpunkter. 4 p.
- Om fel data har presenterats i bilden eller inga mätpunkter syns överhuvudtaget är avdraget 4 poäng.
- Om alla datapunkter inte syns är avdraget 2 poäng och om datapunkterna uppvisas med en streckad linje är avdraget 1 poäng.
- Om axlarna är felsvängda, eller om storhetens eller enhetens beteckningar saknas är avdraget för varje fel 1 poäng.
Typiska fel: Mätresultaten visas med en streckad linje eller en onödig sammankoppling av de uppvisade mätpunkterna med en streckad linje.
2.2 Bestäm utgående från den grafiska presentationen tidpunkten vid vilken badmintonbollen är vid sin högsta punkt. Under vilket tidsintervall är bollens hastighet ungefär konstant? 4 p.
Badmintonbollen rör sig uppåt till en början och dess hastighet är positiv. Bollen har uppnått topphöjden då hastigheten momentant är noll. Utgående från de ritade mätpunkterna kan vi bedöma att det här sker vid tidpunkten t = 0,9 s.
En linje har anpassats till mätpunkterna vid intervallet 0,70 s – 1,15 s. Linjen och dess ekvation visas i bilden i deluppgift 2.1. Ur linjens ekvation kan vi lösa för tiden då v = 0:
t=\frac{0\,{\rm m/s}-9,\!3079\,{\rm m/s}}{-9,\!9434\,{\rm m/s^2}} = 0,\!9361\,{\rm s} \approx 0,\!94\,{\rm s}.Utgående från den grafiska presentationen hålls bollens hastighet ungefärligt konstant vid tidsintervallet 2,4 s – 2,8 s.
Poängsättning:
- Ett resultat intervallet 0,90 s ... 0,95 s har givits. 2 p.
- Det har givits ett tidsintervall med utgångstiden inom intervallet 2,0 s ... 2,4 s och sluttiden vid 2,8 s. 2 p.
För fulla poäng krävs det att svaret har givits med två gällande siffrors noggrannhet. Om slutresultaten givits med större noggrannhet är avdraget 1 poäng från vardera resultatens poäng.
Typiskt fel: För stor noggrannhet.
2.3 För luftmotståndets storlek F_D gäller modellen F_D = \frac{1}{2} C \rho A v^2 där C är en koefficient som beror av kroppens form, \rho är luftens densitet (1,22 kg/m3), A är kroppens tvärsnittsyta och v är kroppens hastighet. Undersök tidsintervallet där bollens hastighet är ungefär konstant. Bestäm koefficienten C för badmintonbollen som använts i experimentet. 7 p.
Enligt Newtons andra lag är kroppens acceleration noll då den totala kraften som påverkar den är noll. Eftersom hastigheten inte förändras i det undersökta intervallet betyder det att krafterna är lika stora.
För krafterna gäller då F_G = F_D, vilket ger
mg = \frac{1}{2}C\rho A v^2.För koefficienten C får vi storhetsekvationen
C = \frac{2mg}{\rho A v^2}Vi beräknar medelvärdet för hastigheternas absolutvärden i tidsintervallet 2,40 s – 2,81 s. Genom tabellberäkning får vi v = 6,5783 m/s.
För tyngdaccelerationen använder vi värdet g = 9,81 m/s2 och för luftens densitet använder vi det givna värdet \rho = 1,22 kg/m3. Vi får
\begin{eqnarray*} C &=& \frac{2mg}{\rho A v^2} = \frac{2\cdot 0,0048\text{ kg}\cdot9,81\text{ m/s}^2}{0,0030\text{ m}^2\cdot1,22\text{ kg/m$^3$}\cdot(6,5783\text{ m/s})^2} \\&=& 0,5946 \approx 0,59. \end{eqnarray*}Poängsättning:
- Newtons II lag eller jämvikt mellan krafterna har använts som motivering. 2 p.
- Det har givits en storhetsekvation löst för den efterfrågade storheten C. 2 p.
- Ett slutresultat inom intervallet 0,59...0,62 har givits med en eller två siffrors noggrannhet. 3 p.
- Om slutresultatet givits med en större noggrannhet är avdraget 1 poäng.
Typiska fel: Motiveringen eller storhetsekvationen för koefficienten C saknas.
3. Effekten hos ett uppvärmningsmotstånd 15 p.
Grafisk presentation:
Poängsättning för den grafiska presentationen:
- Det har presenterats en graf över tvättprogrammens temperatur (eller temperaturskillnader) eller energimängden som använts för att värma vattnet som en funktion av tvättprogrammets längd. Mätresultaten bör synas som enskilda mätpunkter. 5 p.
- Om datapunkterna inte kan urskiljas är avdraget 3 poäng.
- Om datapunkterna visas med en streckad linje är avdraget 1 poäng.
- Om beteckningen för antingen storhet eller enhet saknas från en axel är avdraget 1 poäng för vardera.
- Om en till mätpunkterna anpassad linje saknas från den grafiska presentationen är avdraget 2 poäng.
Ur grafen ser vi sambandet mellan tvättprogrammets temperatur och längd. Riktningskoefficienten för linjen som är anpassad till datapunkterna ger oss vattnets uppvärmningshastighet i alla tvättprogram
\frac{\Delta T}{t}= 1,132\ ^{\circ}{\rm C/min} = 0,0189\ ^{\circ} {\rm C / s}.Det uppvärmda vattnets mängd är hälften av totalförbrukningen:
m= \frac{37 \rm \ l \cdot 1,0 \rm \ kg/l}{2} = 18,5 \rm \ kg.Genom att kombinera uttrycken för uppvärmningsmotståndets effekt P={E}/{t} och värmemängden som tillförs vattnet E=cm \Delta T får vi ett uttryck för effekten
P= \frac{E}{t}\ =cm \frac{\Delta T}{t}.Ur detta får vi uppvärmningsmotståndets effekt
P=4,\!186 {~\rm kJ / kg}\cdot 18,\!5 {~\rm kg} \cdot 0,\!0189\; ^{\circ} {\rm C/ s}=1,\!464 {~\rm kW} \simeq 1,\!5 {~\rm kW.}Uppvärmningsmotståndets effekt är ungefär 1,5 kW.
Poängsättning för uträkningarna:
- Värdet på uppvärmningshastigheten 1.1–1.2 ℃/min (eller 0,018–0,020 ℃/s) eller värdet på effekten 1,4–1,5 kW har avlästs ur den grafiska presentationen. 3 p.
- En storhetsekvation för beräkning av energin med hjälp av den specifika värmekapaciteten har presenterats och använts. 2 p.
- En storhetsekvation för beräkning av effekten utgående från energin har presenterats och använts. 2 p.
- Ett slutresultat inom intervallet 1,4–1,5 kW har givits med två eller tre gällande siffrors noggrannhet. 3 p.
- Om resultatet har erlagts utan att använda en grafisk presentation är avdraget 6 poäng från de totala poängen för uträkningarna.
- Om vattnets mängd inte har delats med två i lösningen är avdraget 3 poäng.
4. Ballong 15 p.
4.1 Vad händer med ballongen när den gnuggas mot kläderna? 3 p.
Då ballongen gnuggas mot kläderna flyttas elektroner från ballongen till kläderna eller tvärtom. På grund av den här triboelektriciteten blir ballongen elektriskt laddad.
Poängsättning:
- Det har berättats att elektroner förflyttas från ballongen till kläderna eller från kläderna till ballongen. 2 p.
- Det har berättats att ballongen laddas elektriskt. 1 p.
Typiska fel: Elektronernas förflyttning eller laddningarnas omfördelning på ballongen har beskrivits. Istället för elektroner talas det om laddningar eller partiklar.
4.2 Förklara varför ballongen fastnar på väggen och hålls kvar där. Namnge krafterna som påverkar ballongen och rita in deras kraftvektorer i bilden som stöd för din förklaring. 8 p.
När den laddade ballongen förs närmare en vägg förorsakar ballongens elektriska fält en polarisering i atomerna och molekylerna på väggens yta. På grund av det här uppstår en elektrisk kraft \bar F_{\rm s} som påverkar ballongen vinkelrätt mot väggen. Väggen påverkar ballongen med en stödkraft \bar N som är lika stor som den elektriska kraften. Ballongen hålls på plats då den uppåtriktade vilofriktionskraften \bar F_{\mu} mellan ballongen och väggen är lika stor som ballongens tyngd \bar G som verkar nedåt. Krafterna är den elektriska kraften, ytans stödkraft, tyngd och vilofriktion.
Poängsättning:
- Det har ritats en kraftfigur i vilken de fyra korrekta krafterna syns. 2 p.
- Ifall en kraft saknas eller figuren innehåller extrakrafter ges inga poäng för kraftfiguren. Ifall längderna för kraftpilarna i kraftfiguren inte står i rätt proportion till varandra är avdraget 1 poäng.
- Alla fyra eftersökta krafter har namngivits. 2 p.
- Ifall högst två av namnen är fel eller saknas är avdraget 1 poäng.
- I förklaring har polarisering eller elektrisk kraft omnämnts. 2 p.
- Betydelsen av friktionen betydelse har konstaterats. 2 p.
Typiska fel: Uppkomsten av den elektriska kraften har beskrivits som om även väggen skulle vara laddad. Motkrafterna till de krafter som påverkar ballongen har även tagits med i betraktelsen. Friktionen har inte tagits i beaktande.
4.3 Varför börjar ballongen efter en stund glida nedåt längs med väggen? 4 p.
Ballongens elektriska laddning avtar med tiden på grund av att det uppstår en elektrisk ström mellan ballongen och väggen. Då ballongens laddning minskar, minskar även den elektriska kraften \bar F_{\rm s} och ytans stödkraft \bar N som väggen påverkar ballongen med. En minskning i stödkraften leder till en minskning i vilofriktionen mellan ballongen och väggen. När laddningen har minskat tillräckligt blir vilofriktionens största värde mindre än tyngden som påverkar ballongen, alltså \mu_0 N<G. Då hamnar ballongen i en nedåtriktad accelererad rörelse.
Poängsättning:
- En minskning av ballongens laddning har omnämnts. 2 p.
- Det har beskrivits hur en minskning av stödkraften påverkar friktionen. 2 p.
Typiskt fel: Det talas om en utjämning av laddningarna eller laddningsskillnaden mellan ballongen och väggen.
5. Gunga 15 p.
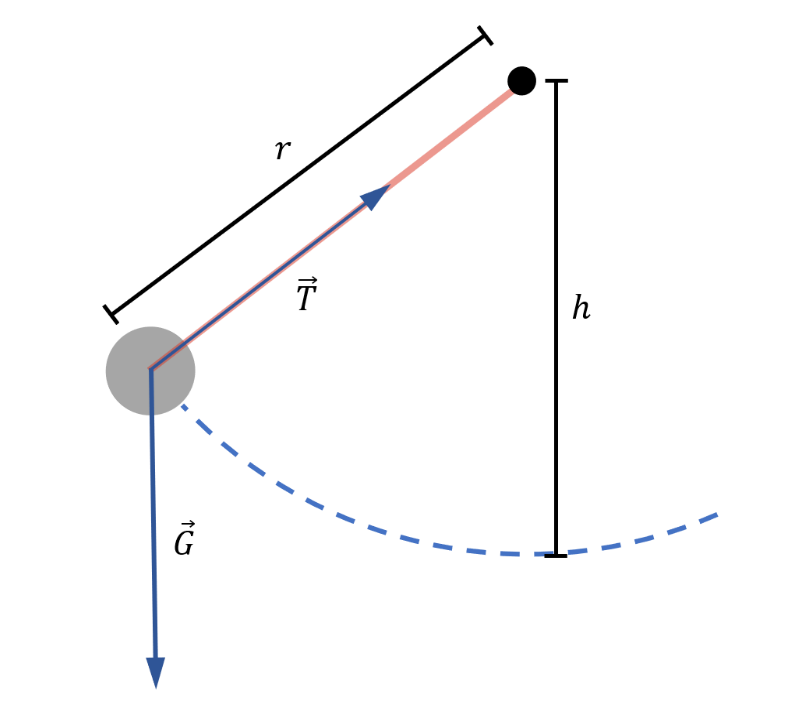
Krafterna som påverkar gungan är gungans och barnets sammanlagda tyngd \overline G = m\overline g och repens sammanlagda spännkraft \overline T.
Gungans rörelse är en centralrörelse, vilket betyder att i riktning med banans normal gäller ekvationen
ma_{\rm n}=T - G_{\rm n},där G_{\rm n} är tyngdens komponent i riktning med banans normal.
För spännkraften får vi ekvationen
T=ma_{\rm n} + G_{\rm n}.Av faktorerna som påverkar spännkraften är G_{\rm n} som störst då gungan är i sitt nedersta läge, varvid G_{\rm n} = G. Även accelerationen a_{\rm n}=v^2/r är som störst i det nedersta läget eftersom hastigheten då är som störst enligt energiprincipen. Belastningen på repen är alltså som störst i det nedersta läget.
Enligt principen om den mekaniska energins bevarande kommer summan av den potentiella energin och den kinetiska energin E_{\rm p}+E_{\rm k} att vara konstant, alltså
\frac{1}{2}m v^2 =mgh,ur vilket vi får kvadraten av gungans maximala hastighet
v^2=2gh.Spännkraften i det nedersta läget är
T=\frac{2mgh}{r}+mg=3mg,eftersom h = r.
Det största värdet för repens spännkraft är
T_{\rm max}=3mg.Detta bör vara mindre än kraften som motsvarar den givna brottgränsen för att repen inte ska brista. Eftersom kraften fördelas på två rep får vi ekvationen
T_{\rm max}<2m_{\rm brottgr\text{ä}ns} galltså
m<\frac{2m_{\rm brottgr\text{ä}ns}}{3}=\frac{2\cdot 65 \;{\rm kg} }{3}\simeq 43\; {\rm kg.}Poängsättning:
- En kraftfigur med de korrekta krafterna under något skede av svängningen har presenterats. 2 p.
- En storhetsekvation för krafterna i normalens riktning eller vid svängningens lägsta punkt har förevisats. 2 p.
- Det har konstaterats att spänningen i repen är som störst då gungan är lodrät. 2 p.
- Det har motiverats korrekt varför spänningen är som störst då repen är lodräta. 2 p.
- Gungans centripetalacceleration har tagits i beaktande. 2 p.
- Bevarandet av den mekaniska energin har använts i lösningen. 2 p.
- En storhetsekvation eller storleken av spänningskraften i (ett eller två av) repen har givits. 1 p.
- Slutresultatet har givits med två gällande siffrors noggrannhet. 2 p.
Typiskt fel: Brottgränsen har beräknats utan att ta i beaktande centripetalaccelerationen och som svar har givits antingen 65 kg eller 130 kg.
6. Tvärflöjt och klarinett 15 p.
6.1 Bestäm frekvensen samt motsvarande våglängd hos grundtonen. 5 p.
I både spektrum A och spektrum B framträder toppen med den lägsta frekvensen och högsta amplituden vid (cirka) 264 hertz. Frekvensen hos grundtonen är alltså f = 264\ {\rm Hz\ (260...270\ Hz)}.
Ur vågrörelsens grundekvation får vi den motsvarande våglängden:
\lambda=\frac{v}{f}=\frac{343\,{\rm m/s}}{264\,{\rm Hz}}\approx 1{\rm ,}3\,{\rm m}.Poängsättning:
- Rätt frekvens, 260...270 Hz, har avlästs från spektret. 2 p.
- En storhetsekvation har givits för våglängden tillsammans med ett värde med två eller tre siffrors noggrannhet. 3 p.
- Om värdet har getts med större noggrannhet är avdraget 1 poäng.
6.2 Redogör med fysikaliska motiveringar för om spektrum A i bild föreställer ett spektrum för tonen spelad med tvärflöjt eller med klarinett. 10 p.
I svaret räcker att någotdera fallet (tvärflöjten eller klarinetten) har behandlats och att rätt lösning har framkommit utgående från detta. Båda alternativen behandlas nedan.
I spektrumen A och B syns grundtonens multipler. I spektrum A framträder de vid 792 Hz och 1 320 Hz, medan de i spektrum B framträder vid 528 Hz, 792 Hz och 1 056 Hz.
Tvärflöjten är ett rör som är öppet i båda ändar. Alla toner (grundtonen och övertonerna) motsvaras då av ljudvågor med antinoder (tryckminimum) i rörets vardera ända. Klarinetten är ett rör som är öppet i ena ändan och slutet i den andra ändan. Alla toner (grundtonen och övertonerna) motsvaras av ljudvågor med en nod (tryckmaximum) vid rörets slutna ända och en antinod (tryckminimum) vid rörets öppna ända. (Beskrivningen kan kompletteras med en bild.)
Om grundtonens våglängd för tvärflöjten är \lambda_1 så har övertonerna våglängderna \lambda_2=\lambda_1/2,\; \lambda_3=\lambda_1/3,\ldots alltså \lambda_n=\lambda_1/n, där n=2,3,\ldots Ur detta följer att övertonernas frekvenser är multipler av grundtonens frekvens 2f_1,\,3f_1,\,4f_1,\ldots alltså f_n=nf_1, där n=2,3,\ldots
Om grundtonens våglängd för klarinetten är \lambda_1, så har övertonerna våglängderna \lambda_2=\lambda_1/3,\; \lambda_3=\lambda_1/5,\ldots alltså \lambda_n=\lambda_1/n, där n=3,5,\ldots Ur detta följer att övertonernas frekvenser är udda multipler av grundtonens frekvens 3f_1,\,5f_1,\,7f_1,\ldots alltså f_n=nf_1, där n=3,5,\ldots
Grundtonernas multipler i spektrum B motsvarar fallet med tvärflöjten och multiplerna i spektrum A motsvarar fallet med klarinetten. Spektrum A föreställer alltså klarinettens spektrum.
Poängsättning:
- Det korrekta frekvenserna har avlästs åtminstone från den ena bilden. 2 p.
- Det har berättats att det uppstår antinoder vid båda ändar av tvärflöjten, eller att det uppstår en antinod i ena ändan av klarinetten och en nod vid den andra. 3 p.
- Med hjälp av våglängderna har frekvenserna för åtminstone den ena av instrumenten klargjorts. 3 p.
- Det har berättats att spektrum A är spektrumet för en klarinett. 2 p.
7. Elektrisk motor 15 p.
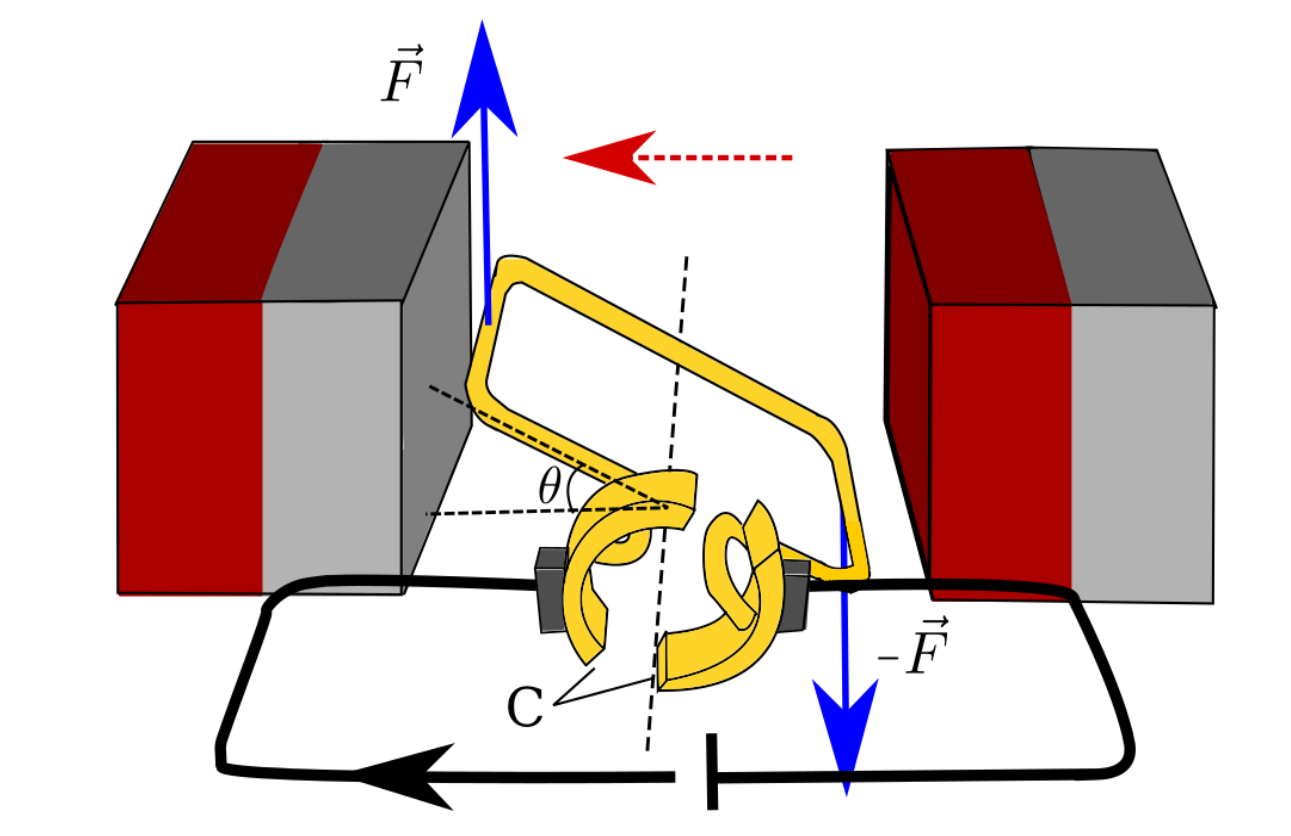
7.1 Rita i bild in kraftvektorerna för krafterna som får slingan att rotera. 4 p.
Krafternas riktningar är vinkelräta mot både magnetfältet och den elektriska strömmen (uppåt och nedåt i bilden) och kraftvektorerna är lika långa.
Poängsättning:
- Båda kraftvektorer har ritats in på de korrekta platserna med de korrekta riktningarna. 4 p.
- Ifall båda krafterna är riktade 180° i fel riktning eller om endast en kraft har ritats in i den korrekta riktningen är avdraget 2 poäng.
7.2 Härled ett uttryck för kraftmomentet M som påverkar slingan som funktion av rotationsvinkeln θ. Vad är kraftmomentets största värde? 8 p.
Krafterna som får slingan att rotera verkar på ledarna som är vinkelräta mot magnetfältets riktning. Storleken hos kraften som verkar på en ledare är
F=IlB,och det totala kraftmomentets storlek är summan av produkterna av båda krafterna och deras momentarmar
\Sigma M=Fa+Fa.Momentarmens längd är a=l/2\cos\theta, där \theta är rotationsvinkeln och l är slingans sidlängd. Det totala kraftmomentet är då
\Sigma M=Il^2 B\cos\theta.Största värdet på kraftmomentet får vi då a=l/2, varvid M=Il^{2}B = 6{,}6\muNm.
Poängsättning:
- Storhetsekvationen för kraften som påverkar en ledare har givits. 2 p.
- Storhetsekvationen för kraftmomentet uttryckt med hjälp av kraften har givits. 2 p.
- Storhetsekvationen för kraftmomentet som funktion av vinkeln θ har givits. 2 p.
- Slutresultatet har givits med två eller tre siffrors noggrannhet. 2 p.
- Om slutresultatet har givits med större noggrannhet är avdraget 1 poäng.
Typiska fel:
- Uppgiften har lösts med hjälp av formeln för kraftmomentet M = NIA\sin(\alpha) i tabellboken. I detta fall kan lösningen ge högst 4 poäng (förutsatt att vinkeln behandlats korrekt).
- Det har utgåtts från kraftens storhetsekvation F = I \ell B \sin(\alpha) med antagande att \theta = \alpha.
7.3 Motorns slinga har en kommutator (markering C i bild ) som byter riktning på den elektriska strömmen i slingan. Varför är det här viktigt för motorns funktion? 3 p.
Kraften som påverkar ledarna beror endast av strömmens och magnetfältets riktningar, inte av ledarens position i magnetfältet. För att motorn ska rotera krävs det att kraftens riktning måste förändras när ledaren rör sig över eller under ledningsslingans axel. Kommutatorn får det här att ske.
Poängsättning:
- Rotationens fortskridande har beskrivits korrekt. 3 p.
8. Fusion 15 p.
8.1 Förklara funktionsprincipen för en fusionsreaktor. 9 p.
Vid fusion går två lätta atomkärnor ihop till en tyngre kärna samtidigt som energi frigörs. Med den frigjorda energin produceras vattenånga som driver en elektisk generator. Tunga isotoper av väte, deuterium och tritium, används i fusionsreaktorer.
Fusion är svårt att få till stånd då de positivt laddade atomkärnorna repellerar varandra på grund av den elektromagnetiska växelverkan. För att få kärnorna tillräckligt nära varandra måste vätets isotoper värmas upp till en mycket hög temperatur varvid de bildar ett plasma. Plasmat hålls ihop med hjälp av magnetfält eller laserstrålning som förhindrar att plasmat kolliderar med reaktorns väggar.
Poängsättning:
- Det har berättats att två lätta kärnor bildar en tyngre kärna och att det frigörs energi vid reaktionen. 4 p.
- Ifall frigöringen av energi saknas är avdraget 2 poäng.
- Den repellerande kraften mellan kärnorna och behovet av en hög temperatur för att överkomma den har onämnts. 3 p.
- Det har nämnts att magnetfält behövs för att hålla ihop plasmat. 2 p.
Typiska fel:
- Det har påståtts att atomer eller partiklar går samman vid fusion.
- Det har påståtts att magnetfältet skapar en hög temperatur.
8.2
Vi antar att fusionsenergi i framtiden kan ersätta fissionsenergi på bred front. Begrunda följande påståenden angående fissionskraftverk. Gäller de även för fusionskraftverk? Motivera ditt svar.
- Det är svårt att hitta en lämplig byggplats för kraftverket.
- Förvar av avfallet som kraftverket producerar är problematiskt.
- För en del stater är det politiskt svårt att få en reaktor på grund av deras internationella relationer.
6 p.
- a) En okontrollerad kedjereaktion kan inte uppstå i en fusionsreaktor, och därför kan en härdsmälta inte ske vid händelse av ett fel i kylsystemet. På grund av det här är det enklare att hitta en lämplig byggplats för kraftverket.
- b) Aktiviteten hos det tritium som används i fusionsreaktorn är mycket hög och som ett material i gasform kan det effektivt spridas från reaktorn som följd av en tillräckligt allvarlig olycka. På grund av det här är det inte nämnvärt enklare att placera en fusionsreaktor än en fissionsreaktor.
- a) I båda reaktorer uppstår kortlivat (under 30000 år) radioaktivt avfall som följd av byggnadsmaterialens exponering. Förvar av det här avfallet är liknande som förvaret av kortlivat avfall från fusionsreaktorer.
- b) Radioaktivt avfall (med mycket lång halveringstid) produceras inte i en fusionsreaktor. Förvar av avfallet från en fusionsreaktor är därmed enklare.
- a) Fissionsdugligt material används inte i fusionsreaktorer. Därför kan man inte direkt bygga kärnvapen med hjälp av dem och därför skulle man inte på samma sätt försöka förhindra anskaffandet av dem i den internationella politiken.
- b) Neutronerna som uppstår i båda reaktorer kan användas för att producera kärnsprängämnen, alltså kommer liknande internationella restriktioner att anpassas även till fusionsreaktorer.
Poängsättning:
En korrekt motivering antingen för eller emot (a eller b) för varje påstående samt den korrekta slutsatsen utgående från den. För varje delfråga. 2 p.
Typiskt fel: Svaret har inte motiverats med hjälp av fysikaliska argument.
Del 3: 20-poängsuppgifter
9. Kokplattor 20 p.
9.1 Beskriv i allmänna drag hur du jämför kokplattornas energieffektivitet. Hur och vad mäter och bestämmer du? Specificera vilka faktorer man måste beakta för att resultaten ska vara så tillförlitliga som möjligt. 10 p.
Vatten värms på vardera kokplattan samtidigt som man mäter hur snabbt vattnet blir uppvärmt i förhållande till den använda elektriska effekten. De uppmätta storheterna är vattnets temperatur och kokplattans mottagna elektriska effekt eller elektriska energi. Den elektriska energin kan mätas med en kWh-givare och den elektriska effekten antingen med en effektgivare eller genom att mäta strömmen och spänningen.
Under mätningarna bör man bevara (eller kontrollera) experimentets utgångstillstånd, till vilket hör åtminstone vattenmängden och vattnets, uppvärmingskärlets och kokplattans utgångstemperaturer. De yttre förhållandena bör även vara desamma under alla mätningar, och samma eller likadana kokkärl bör användas i experimentet.
Poängsättning:
- Det har beskrivits antingen en mätning av vattnets temperatur som funktion av tiden under uppvärmning eller en mätning av tiden det tar att värma upp vatten tills det kokar. 2 p.
- Energins uppmätning med en kWh-givare, effektens uppmätning med en effektmätare, eller en uppmätning av strömmen då spänningen är känd har beskrivits. 3 p.
- Det har berättats att vattnets mängd och utgångstemperatur måste bestämmas. 3 p.
- Det har berättats att likadana eller samma kärl måste användas och att kärlets utgångstemperatur måste vara samma. 2 p.
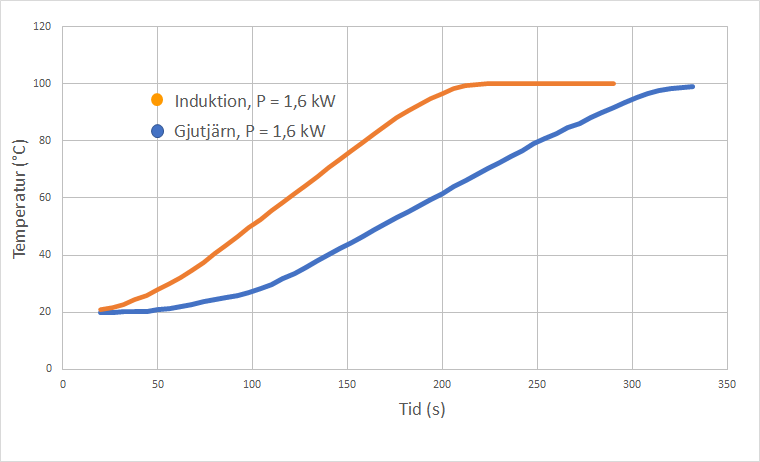
9.2 Skissera en grafisk presentation över hurdana mätdata du förväntar dig att mätningarna ska ge. Om du vill kan du använda dig av bilden i material som hjälp i din presentation. 6 p.
Vattnets temperatur börjar stiga snabbare på induktionsplattan och ökningen är hela tiden snabbare än för gjutjärnsplattan. Vattnets kokpunkt (eller någon annan eftersökt temperatur) uppnås alltså snabbare med en induktionsplatta än med en gjutjärnsplatta.
Poängsättning:
- En grafisk presentation över den förväntade temperaturen som funktion av tiden har förevisats. Två korrekta namngivna kurvor och namngivna axlar måste synas i presentationen. 2 p. De här poängen ges inte om temperaturökningen sker med samma riktningskoefficient för båda plattorna eller om uppvärmningen accelereras med tiden.
- Ur bilden framgår det att kurvorna börjar stiga från samma utgångstemperatur vid olika tidpunkter eller med olika riktningskoefficienter. 2 p.
- Ur bilden framgår det att kurvorna uppnår samma sluttemperatur vid olika tidpunkter eller olika temperaturer på samma tid. 2 p.
9.3 I undersökningarna visar det sig att den ena kokplattan är energieffektivare. Vilka är de fysikaliska orsakerna till skillnaden i energieffektivitet? 4 p.
Induktionsplattan är energieffektivare. Den värmer kokkärlet direkt i stället för att värma ett stort järnstycke som gjutjärnsplattan. De uppvärmda kropparnas (kokplatta + kokkärl + vatten) totala värmekapacitet är därför mindre. Induktionsplattans keramiska yta är en dålig värmeledare, vilket gör att endast en liten mängd värmeenergi överförs till den från kokkärlet. Induktionsplattan värms inte heller upp mera än till vattnets kokpunkt. Gjutjärnsplattan måste för sin del värmas upp till en betydligt högre temperatur än 100 grader Celsius för att värmet ska överföras tillräckligt snabbt till kokkärlet. Ju svalare kokplattan hålls när vattnet kokas, desto mindre strålar och leds energi bort från den till omgivningen.
Poängsättning:
- Ur svaret framgår det att induktionsplattan inte värms upp. 2 p.
- Det har konstaterats att på grund av dess lägre temperatur överför induktionsplattan mindre energi till omgivningen än gjutjärnsplattan. 1 p.
- Det har konstaterats att induktionsplattan överför mindre energi till omgivningen på grund av att den har en lägre värmeledningsförmåga. 1 p.
10. Radiometrisk mätning 20 p.
10.1 Skriv ut sönderfallsekvationen för alfasönderfallet av isotopen Am-241 och förklara kortfattat varifrån gammakvantumet kommer. 4 p.
I samband med sönderfallet uppstår en exciterad Np-237-kärna. När excitationstillståndet återgår till grundtillståndet emitterar kärnan ett gammakvantum.
Poängsättning:
- Den korrekta sönderfallsekvationen har givits. 2 p.
- Det har berättats att gammakvantumet uppstår när kärnans excitationstillstånd återgår till grundtillståndet. 2 p.
Typiskt fel: Det har berättats att strålningen uppstår då atomens excitationstillstånd återgår till grundtillståndet.
10.2 Visa att ekvationen \Delta\mu= \displaystyle{\frac{1}{x}}\ln\left(\displaystyle{\frac{I_2}{I_1}}\right) gäller för skillnaden mellan vätskans och gasens absorptionskoefficienter \Delta \mu=\mu_1-\mu_2. 4 p.
Absorptionslagen: I=I_0 e^{-\mu x}. Totalintensiteten då det endast finns vätska i röret: I_1=I_0 e^{-\mu_1 x}. Totalintensiteten då det endast finns gas i röret: I_2=I_0 e^{-\mu_2 x}. Ur de här får vi:
\ln\left(\frac{I_1}{I_0}\right) =\ln I_1 -\ln I_0 =-\mu_1 x,\\ \ln\left(\frac{I_2}{I_0}\right) =\ln I_2 -\ln I_0 =-\mu_2 x.Differensen av de föregående ekvationerna ger oss
\ln I_2-\ln I_1 =\ln\left(\frac{I_2}{I_1}\right)=\mu_1 x -\mu_2 x =x(\mu_1-\mu_2) = x\Delta\mu.och då vi delar med medeltjockleken får vi
\Delta\mu= \frac{1}{x} \ln\left(\frac{I_2}{I_1}\right)\!,och då kan vi konstatera att ekvationen gäller för skillnaden mellan absorptionskoefficienterna.
Poängsättning:
- Intensiteterna I1 och I2 har givits med hjälp av absorptionslagen 2 p. och den efterfrågade storhetsekvationen har härletts korrekt. 2 p.
Typiskt fel: Absorptionslagen i formen I_2=I_1 e^{-\Delta\mu x} har använts som utgångsläge.
10.3 För vätske-gasblandningen kan man introducera en så kallad effektiv absorptionskoefficient \mu=\mu_1-\alpha(\mu_1-\mu_2) där \alpha är gasens relativa andel av vätske-gasblandningens volym. Anta att flödeshastigheten är konstant och att mätvärdena har erhållits vid jämna tidsintervall. Rörets geometri påverkar inte intensitetsmätningarna. Bestäm det procentuella medelvärdet för gasens andel av materialet som flödar i röret under hela mätningen (bild och mätdata ). Ge ditt svar med tre gällande siffrors noggrannhet. 8 p.
Utgångsläge: \mu=\mu_1 -\alpha(\mu_1 -\mu_2) och uttrycket för \Delta\mu från deluppgift 10.2. Skillnaden mellan den uppmätta maximala absorptionskoefficienten och den momentana effektiva absorptionskoefficienten för materialet som flödar i röret kan beräknas med hjälp av den momentana intensiteten och den uppmätta minimiintensiteten. Om vi använder oss av ekvationen som härletts i föregående deluppgift för skillnaden mellan absorptionskoefficienterna får vi
(\mu_1-\mu)=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!.Genom att substituera in det givna uttrycket för effektiva absorptionskoefficienten
\mu=\mu_1-\alpha(\mu_1-\mu_2)får vi (\mu_1-\mu)= \mu_1-[\mu_1-\alpha(\mu_1-\mu_2)]=\alpha(\mu_1 -\mu_2)=\alpha\Delta \mu alltså är
\alpha\Delta \mu=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!.Genom att använda uttrycket för \Delta\mu från deluppgift 10.2 ger det här oss ekvationen
\frac{\alpha}{x}\ln\left(\frac{I_2}{I_1}\right)=\frac{1}{x} \ln\left(\frac{I}{I_1}\right)\!alltså
\alpha= \frac{\ln\left(I/I_1\right)}{\ln\left(I_2/I_1\right)}.För varje uppmätt momentana intensitet I_i kan vi beräkna gasens motsvarande relativa andel av den totala mängden material \alpha_i. Flödeshastigheten är konstant och mätvärdena har erhållits vid jämna tidsintervall, vilket betyder att gasens andel av det totala materialet under hela mätningen är medelvärdet av alla \alpha_i-värden, alltså
\alpha_{\rm m}=\frac{1}{N}\sum\alpha_i =\frac{1}{N}\sum \frac{\ln\left(\displaystyle{\frac{I_i}{I_1}}\right)}{\ln\left(\displaystyle{\frac{I_2}{I_1}}\right)}.Med hjälp av ett tabellprogram kan vi estimera intensitetens maximi- och minimivärden. Minimiintensiteten kan beräknas från intensitetens medelvärde under tidsintervallet 1 870 ms – 2 030 ms:
I_1=37,\!992251\, {\rm cpms}\approx 38\ {\rm cpms}\, (\pm 1\, {\rm cpms}).och maximiintensiteten kan uppskattas genom att beräkna intensitetens medelvärde under tidsintervallet 1 440 ms – 1 710 ms:
I_2=50,\!340521\, {\rm cpms}\approx 50 {\rm cpms}\, (\pm 1 \, {\rm cpms}).Genom tabellberäkningar får vi medelvärdet för gasens relativa andel
\alpha_{\rm m} =0,\!378235\approx 38 \% \,(\pm 1 \%).Poängsättning:
- Idén om en jämförelse mellan den momentana intensiteten och maximi/minimiintensiteten har framförts. 2 p.
- Maximi- och minimivärdena för intensiteten har bestämts. 2 p.
- En slutekvation har härletts för α. 2 p.
- Rätt svar har givits med 2-3 gällande siffrors noggrannhet. 2 p.
- Ifall svaret har givits med större noggrannhet är avdraget 1 poäng.
10.4 Hur mycket förändras skillnaden mellan maximiintensiteten och minimiintensiteten \Delta I_0=I_1-I_2 på tio år? 4 p.
Sönderfallslagen: I=I_0 e^{\displaystyle{{-\lambda t}}}, där \lambda =\displaystyle{\frac{\ln 2}{T_{1/2}}} och T_{1/2}=432,\!2 år.
Intensitetsskillnaden \Delta I_0=I_2-I_1 =50,\!340521\; {\rm cpms}-37,\!992251\;{\rm cpms}=12,\!348270 \;{\rm cpms}.
Skillnaden i intensitet blir
\Delta I_{10}=\Delta I_0e^{\displaystyle{t {\ln 2}/{T_{1/2}}}}=12,\!348270\, {~\rm cpms}\cdot e^{\displaystyle{({\ln 2}/{432,\!2\, {\rm a}}})10 {\rm a}}=12,\!151812\, {~\rm cpms}.\Delta I_{0}-\Delta I_{10}=12,\!348270\, {\rm cpms}-12,\!151812\, {\rm cpms}=0,\!196458\, {\rm cpms}\approx 0,\!20\, {\rm cpms} (\pm {\rm 0,02 cpms)}.
Poängsättning:
- Sönderfallslagen har använts på så sätt att λ har rätt enhet. 2 p.
- Slutresultatet har givits med 1-3 gällande siffrors noggrannhet. 2 p.
- Ifall svaret har givits med större noggrannhet är avdraget 1 poäng.
11. Mätning av styrkan hos ett gravitationsfält 20 p.
11.1 Varför och hur påverkas satelliternas rörelse av lokala förändringar i jordklotets massa? Varför behövs det två satelliter? 4 p.
I områden där mycket massa har koncentrerats påverkas satelliterna av en större gravitationskraft än i andra områden. När en satellit närmar sig ett sådant område ökar dess hastighet och när den avlägsnar sig därifrån så minskar dess hastighet.
Det behövs två satelliter för att förändringarna i satelliternas hastigheter bedöms utgående från förändringar i avståndet mellan dem.
Poängsättning:
- Följande tankekedja har förevisats: en större massa förorsakar en större gravitationskraft, vilket i sin tur förorsakar en högre hastighet. 2 p.
- Det har berättats att hastighetsförändringen kan bestämmas genom en uppmätning av avståndet mellan satelliterna. 2 p.
11.2 Varför syns till exempel inte bergskedjorna eller andra formationer på jordytan i bilden i material ? 3 p.
Grafen presenterar förändringen i gravitationsfältets styrka jämfört med medelvärdet över en period på tre år. Bergskedjor och andra terrängformationer är oförändrade på den här tidsskalan, alltså syns de inte i bilden.
Poängsättning:
- Det framgår att en lång tids medeltal används som jämförelse vid mätningarna och att de uppmätta förändringarna sker på en kortare tidsskala än förändringar av jordytans former. 3 p.
11.3 Hur stor relativ förändring i satelliternas tyngdacceleration kan GRACE-anordningen enligt materialet detektera? 8 p.
I materialet konstateras att anordningen kan detektera förändringar i gravitationsfältet som förorsakas av en cirkulär vattenmassa med diametern d=300 km och tjockleken PUUTTUVA cm. Massan av en sådan skiva är
M=\frac{\pi d^2}{4}h\rho \approx 7 \cdot 10^{11} \rm{kg},där \rho är vattnets densitet. Vattenmängden är inte punktformad, men vi uppskattar ändå gravitationskraften som den förorsakar med hjälp av ekvationen
F=\gamma \frac{mM}{r^2},där \gamma är Newtons gravitationskonstant, m är satellitens massa och r är höjden för satellitens omloppsbana.
Utgående från Newtons andra lag är förändringen i tyngdaccelerationen på grund av vattenmängden
\Delta a=\frac{F}{m}=\gamma\frac{M}{r^2} \approx 1,88\times 10^{-10} \rm{m/s^2}.Den relativa förändringen i tyngdaccelerationen i förhållande till tyngdaccelerationen förorsakad av jorden är
\frac{\Delta a}{g}=\gamma\frac{M}{gr^2}=\gamma\frac{\displaystyle{\frac{\pi d^2}{4}}h\rho}{gr^2}\approx 2\times 10^{-11}.Poängsättning:
- En storhetsekvation för vattenskivans massa har förevisats antingen skilt eller som del av den slutliga storhetsekvationen. 2 p.
- Uttrycket för gravitationskraften har använts för att bestämma något för lösningen relevant. 2 p.
- Uttrycket för den relativa förändringen har givits. 2 p.
- Ett slutresultat med 1-2 gällande siffrors noggrannhet har givits. 2 p.
- Ifall en större noggrannhet har givits är avdraget 1 poäng.
11.4 Hurdan information kan man få genom mätningar av gravitationsfältet som kan vara svår att få genom andra mätmetoder? 5 p.
Förändringarna i gravitationsfältet är förorsakade av massan. Genom mätningar av gravitationsfältet får man alltså information om jordklotets massfördelning. Förutom kraftiga jordbävningar är förändringar i massan i synnerhet kopplade till förflyttningar av vatten och is. Förflyttning av vatten och is som inte syns är svår att mäta på andra sätt. Exempel på sådana är underjordiska vattenreservoarer och vatten- eller ismassor som är fördelade över ett stort område.
Poängsättning:
- En uppmätning av förändringar i jordklotets massfördelning har identifierats. 3 p.
- En uppmätning av förändringar i vatten- eller ismassor eller förflyttning av massor på grund av vulkanisk aktivitet har omnämnts. 2 p.
- Ifall det inte utgår från svaret att förändringarna i massor eller massfördelningar som uppmäts sker på korts tidsskalor är avdraget 2 poäng.