Beskrivningar av goda svar: SV – Fysik
30.3.2022
Slutgiltiga beskrivningar av goda svar 17.5.2022
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl färmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
För felaktigt antal gällande siffror görs i studentprovet våren 2022 ett avdrag på en poäng för varje svar som givits med fel noggrannhet om inte annat angetts i uppgiften.
Del 1: 20-poängsuppgift
1. Flervalsuppgifter från fysikens olika delområden 20 p.
1.1 I ett stående längdhopp strävar man efter att komma så långt framåt som möjligt utan anlopp. Vad kan du säga om den totala kraften som påverkar hopparen vid avstampet? 2 p.
- Den totala kraften är riktad snett framåt och uppåt. (2 p.)
1.2 Bilarna A och B färdas längs med samma cirkelbana i en rondell. Bil A har hastigheten 20 km/h och bil B har hastigheten 40 km/h. Vilket av följande påståenden är sant? 2 p.
- Bil B har en fyra gånger så stor acceleration som bil A. (2 p.)
1.3 Vad händer med luften inuti en ballong då ballongen plötsligt punkteras? 2 p.
- Volymen ökar och temperaturen minskar. (2 p.)
1.4 Vi undersöker två slutna strömkretsar med identiska ackumulatorer som strömkällor. En glödlampa är kopplad till strömkrets 1 och två glödlampor är parallellkopplade till strömkrets 2. Alla lampor är likadana. Vilket av följande påståenden är sant? 2 p.
- Alla tre lampor lyser lika starkt. (2 p.)
1.5 En elektron kommer in i ett homogent elektriskt fält vinkelrätt mot fältlinjerna. Hur beter sig elektronen när den kommit in i det elektriska fältet? 2 p.
- Elektronens bana böjer sig tills rörelsen sker ungefär i riktning längs med fältlinjerna. (2 p.)
1.6 Biljardboll A kolliderar med en likadan boll B som är stillastående. Boll A stannar vid kollisionen, medan boll B börjar röra sig framåt. Vi antar att kollisionen är elastisk. Vilket av följande påståenden gällande den totala rörelsemängden och bollarnas sammanlagda rörelseenergi är sant? 2 p.
- Både rörelsemängden och rörelseenergin bevaras. (2 p.)
1.7 En skyskrapas höjd är 400 m och vid starka vindar svänger dess spets periodiskt från det ena extremläget till det andra. Hur lång är våglängden för grundvibrationen som fortplantas genom skyskrapan? 2 p.
- 1 600 m (2 p.)
1.8 Ljudnivån från en tryckluftsborr är 100 dB på 10 meters avstånd från borren. Vilken är den sammanlagda ljudnivån som uppstår från två tryckluftsborrar på samma avstånd? 2 p.
- 103 dB (2 p.)
1.9 Då en ledningsslinga roteras i ett magnetfält induceras en källspänning i slingan. Vilken av följande förändringar ökar mest på toppvärdet för källspänningen som induceras i slingan? 2 p.
- Rotationshastigheten fyrdubblas. (2 p.)
1.10 Elektroner frigörs från ett metallstycke med en laserpuls. Hur kan man öka rörelseenergin hos elektronerna som frigörs? 2 p.
- Genom att öka frekvensen hos laserpulsens ljus. (2 p.)
Poängsättning:
Rätt svar. (2 p.)
Del 2: 15-poängsuppgifter
2. Vindkraftverk 15 p.
2.1
Rotorns storlek har en betydande inverkan på den elektriska effekt som ett vindkraftverk producerar. Rotorns storlek beskrivs med svepytan, vilken är arean för cirkeln som spetsen av rotorbladen rör sig längs med (material ).
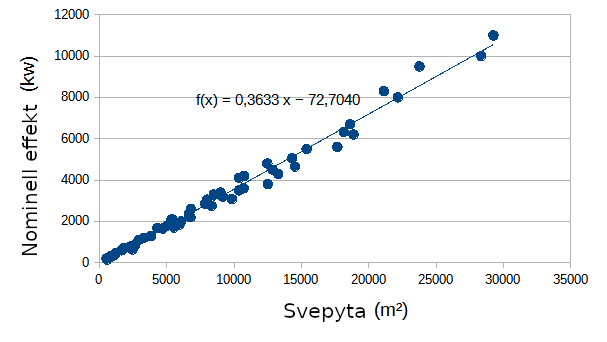
Tabell visar de effekter tillverkarna har angett för olika vindkraftverk. Bestäm utgående från informationen i tabellen och med hjälp av en grafisk framställning hur mycket vindkraftverkets effekt vanligtvis ökar om rotorns svepyta ökar med 25 m2.
12 p.
För varje vindkraftverk i tabellen kan rotorns svepyta beräknas med hjälp av rotorns diameter d:
A= \pi \cdot \left(\displaystyle{\frac{d}{2}}\right)^2.
Hur kraftverkens effekt beror av svepytan kan vi se genom att sätta in datapunkterna i ett A,P-koordinatsystem.
Riktningskoefficienten för en linje som är anpassad till datapunkterna beskriver hur effekten förändras då svepytan ökar:
k = \displaystyle{\frac{\Delta P}{\Delta A}} = 0{,}3633 \ \frac{\rm kW}{\rm m^2}.
Ur det här följer att effekten ökar med
\Delta P = k \cdot \Delta A = 0{,}3633 \ \displaystyle{\frac{\rm kW}{\rm m^2}} \cdot 25 \rm \ m^2 = 9{,}083 \ \rm kW \approx 9{,}1 \rm \ kW.
Effekten för ett typiskt vindkraftverk ökar med ungefär 9,1 kW när svepytan ökar med 25 m2.
Poängsättning:
Typiskt fel:
2.2 Namnge tre delområden inom de fysikaliska vetenskaperna vars expertis krävs i samband med planering eller byggande av vindkraftverk. 3 p.
Exempel på delområden inom de fysikaliska vetenskaperna vars expertis krävs i samband med planering och byggande av vindkraftverk är
- våg(rörelse)lära
- aerodynamik
- akustik
- energiteknik
- geofysik/geologi
- hållfasthetslära
- värmelära/termodynamik/termofysik
- materialvetenskap/-teknik
- mekanik
- meteorologi
- elteknik/ellära/elektromagnetism
- flödesmekanik
- miljöteknik.
Poängsättning:
Typiskt fel:
3. Kompression av en gas 15 p.
3.1 Bestäm gasens tryck då gasens temperatur har uppnått sluttemperaturen 24 ˚C. 8 p.
Luften kan antas bete sig som en ideal gas vid de givna förhållanden, alltså använder vi tillståndsekvationen för en idealgas, pV = nRT, där R är den allmänna gaskonstanten och n är gasens substansmängd. För att lösa uppgiften räcker det med att undersöka utgångsläget och slutläget. Gasens (luftens) utgångstemperatur är T_1 = 5 \,^{\circ}\mathrm{C} = 278,15 K och sluttemperaturen är T_2 = 24\,^{\circ}\mathrm{C} = 297,15 K, volymen i början är V_1 = 1{,}1\cdot 10^{-3}\, {\rm m}^3 och i slutet V_2 = 0{,}38\cdot 10^{-3}\, {\rm m}^3. Gasens tryck i början är p_1 = 101 kPa. Vi betecknar trycket i slutet med p_2.
Eftersom gasens substansmängd inte förändras kan vi utgående från tillståndsekvationen för en idealgas skriva
p_1 \displaystyle{\frac{V_1 }{T_1}} = p_2 \displaystyle{\frac{V_2 }{T_2}}.
Gasens tryck i slutet ärp_2 = p_1 \displaystyle{\frac{ V_1 T_2}{ V_2 T_1}} \approx 310\, {\rm kPa}.
Poängsättning:
Typiskt fel:
3.2
Använd dig av begreppen värme och arbete för att förklara vilka förändringar som sker i gasens inre energi
- vid kompression av gasen
- när gasens temperatur förändras och närmar sig laboratoriets temperatur.
7 p.
Enligt termodynamikens första huvudsats ändrar gasens inre energi U då energi överförs som värme (Q) mellan gasen och omgivningen eller då gasen utför arbete (W) på omgivningen eller då omgivningen utför arbete på gasen. Uttryck som storhetsekvation gäller \Delta U = Q + W.
Då kolven trycks in utför kraften ett arbete på gasen, varvid gasens inre energi ökar och gasens temperatur stiger. Med hjälp av tillståndsekvationen för en ideal gas kan vi beräkna temperaturen genast efter kompressionen till 150 ˚C. Temperaturutjämningen till 24 ˚C betyder att temperaturen sjunker. Då överförs energi som värme till omgivningen och gasens inre energi minskar. Gasens inre energi är aningen större i slutet än den var i början.
Poängsättning:
Typiska fel:
4. Fotomotstånd 15 p.
4.1 Vad är det största värdet på belysningsstyrkan för vilket LED-lampan fortfarande lyser? 3 p.
Utgående från simuleringen tänds LED-lampan då belysningsstyrkan är 24,3 lx eller mindre.
Poängsättning:
Typiskt fel:
4.2 Vad är värdet på LED-lampans tröskelspänning? 3 p.
Då LED-lampan tänds är spänningen över förmotståndet U_1 = 2,9 V. Eftersom källspänningen är E = 5,0 V blir LED-lampans tröskelspänning U_2 = E-U_1 = 2,1 V.
Poängsättning:
Typiskt fel:
4.3 Vilka är värdena på resistanserna hos motstånden R1 och RLDR då belysningsstyrkan är 540 lx? 4 p.
R_1 = \displaystyle{\frac{4{,}591\, \mbox{V}}{0{,}675 \,\mbox{mA}}}=6{,}8\, \mbox{ k}\Omega.
Då är tröskelspänningen U_2 = E-U_1 = 0{,}409\, \mbox{V}. Samma elektriska ström går genom båda motstånden, alltså är fotomotståndets resistans
R_{\rm LDR} = \displaystyle{\frac{0{,}409\,\mbox{V}}{0{,}675\, \mbox{mA}}} = 610\, \Omega.
Poängsättning:
4.4 Vi undersöker de värden för belysningsstyrkan för vilka LED-lampan inte lyser. Ökar eller minskar resistansen hos fotomotståndet i kretsen då belysningsstyrkan ökar inom de här värdena? 5 p.
Tidigare beräknades att R_{\rm LDR} = 610\, \Omega när belysningsstyrkan är 540 lx. Vi undersöker situationen när belysningsstyrkan är 900 lx. Då är
R_{\rm LDR}(900\mbox{ lx}) = \displaystyle{\frac{(5{,}0-4{,}703)\, \mbox{V}}{0{,}692\, \mbox{mA}}} = 430\, \Omega,
alltså minskar resistansen när belysningsstyrkan ökar. Genom att pröva sig fram i simuleringen märker man att en större belysningsstyrka alltid leder till en högre uppmätt spänning när LED-lampan inte lyser. Därmed måste fotomotståndets resistans minska när belysningsstyrkan ökar.
Poängsättning:
Typiskt fel:
5. En hiss 15 p.
5.1 Då hissen står stilla hänger studenten sin telefon i fjädervågens krok. Vågen visar värdet 1,93 N. Då hissen börjat röra på sig visar vågen värdet 2,23 N. I vilken riktning och med hur hög acceleration rör sig hissen? 8 p.
Vi ritar en kraftfigur för telefonen då hissen står still. Då är telefonens acceleration noll och ur dynamikens grundlag \Sigma{\vec F} =m{\vec a} följer då skalärekvationen (vi väljer riktningen uppåt som positiv riktning)
T_1-mg=0,
där T_1 är kraften som fjädervågen påverkar telefonen med och m är telefonens massa. Ur det får vi telefonens massa
m=\displaystyle{\frac{T_1}{g}} = \displaystyle{\frac{1{,}93\; {\rm N}}{9{,}81\; {\rm m/s^2}}}=0{,}196738\; {\rm kg}.
Då hissen har börjat röra sig har den och telefonen accelerationen \vec a. I skalärform är dynamikens grundlag
T_2-mg=T_2-T_1 =ma,
där T_2 är kraften som fjädervågen påverkar telefonen med under den accelererade rörelsen. Som acceleration får vi
a=\displaystyle{\frac{T_2-T_1}{m}}=\frac{2{,}23\; {\rm N}-1{,}93\; {\rm N}}{0{,}196738\; {\rm kg}}\approx 1{,}52\; \frac{\rm m}{\rm s^2}.
Hissen accelererar uppåt eftersom a är positivt. Hissen startar från stillastående och rör sig uppåt.
Poängsättning:
Typiskt fel:
5.2 Studenten märker att fjädern töjer med 4,5 cm mer då hissen börjar röra på sig. Hur stor är fjädervågens fjäderkonstant? 7 p.
Utgående från Newtons II lag, och genom att använda fjäderns kraft, kan man skriva för telefonen i jämvikt
kx_{\rm 1} – mg = 0och för telefonen i accelererad rörelse
kx_{\rm 2} – mg = madär x_{\rm 1} är fjäderns uttöjning då hissen är stillastående och x_2 = x_1+\Delta x är fjäderns uttöjning då hissen är i accelererad rörelse. De extra töjningen \Delta x = 4{,}5\;{\rm cm}. Ur ekvationssystemet får vi
k \Delta x = maGenom att substituera för uttrycket som erhölls i den tidigare deluppgiften
ma = T_{\rm 2} – T_{\rm 1}får vi som fjäderkonstant
k = \frac{T_2-T_1}{x}=\frac{2{,}23\; {\rm N}-1{,}93\; {\rm N}}{0{,}045\; {\rm m}}\approx 6{,}7\; \frac{\rm N}{\rm m}.
Alternativ metod:
Vi bildar ett ekvationssystem med hjälp av Hookes lag
Genom att lösa det får vi samma storhetsekvation för fjäderkonstanten som ovanför.
Poängsättning:
Typiska fel:
6. Östersjöns vågor 15 p.
6.1 Hur stor har amplituden för Östersjöns högsta enskilda vågor varit? 2 p.
- 7 (2 p.)
6.2 Hur hög är frekvensen för de högsta vågorna vid typisk sjögång på Östersjön? 2 p.
- 0,2 (2 p.)
Även 0.2 Hz godkändes som rätt svar.
6.3 Med hur stor hastighet framskrider de högsta vågorna vid typisk sjögång på djupt vatten i Östersjön? 2 p.
- 8 (2 p.)
6.4 Utgående från den givna informationen om vågorna kan vi härleda att ett typiskt djup i Östersjön vanligtvis är mindre än 2 p.
- 130 m (2 p.)
6.5 Utgående från den givna informationen om vågorna kan vi härleda att ett typiskt djup i Östersjön vanligtvis är större än 2 p.
- 20 m (2 p.)
6.6 Vad betyder termen svepsträcka som används i materialet? 2 p.
- Sträckan som vinden fritt har kunnat öka på sjögången ända tills den nått observationsplatsen (2 p.)
6.7 Vi undersöker allmänt en situation där vattnets vågor närmar sig stranden snett. Stranden är långgrund. Vilken av följande egenskaper hos vågrörelsen ändras inte? 3 p.
- Frekvensen (3 p.)
Poängsättning:
7. Dimkammare 15 p.
7.1 Bestäm förtecknet för partikelns laddning och partikelns massa. 11 p.
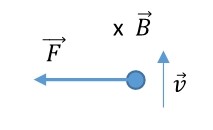
Kraften \vec F som påverkar partikeln är riktad vinkelrätt mot både hastigheten \vec v och magnetfältet \vec b. Enligt regeln för den magnetiska kraftens riktning upplever en positivt laddad partikel en kraft mot vänster, och en negativt laddad partikel upplever en kraft mot höger. För att partikeln ska färdas längs med en cirkelbana måste kraften som påverkar den vara riktad mot centrumet för krökningen, alltså mot vänster. Partikeln har alltså en positiv laddning. Kraftfiguren här intill visar riktningen för kraften som påverkar en positiv partikel.
Beloppet på kraften \vec F är F=qvB eftersom partikelns hastighet är riktad vinkelrätt mot magnetfältet. Enligt Newtons II lag kan vi skriva qvB=ma. Acceleration i en jämn cirkelrörelse är a=v^2/r. Vi får ekvationen qvB=mv^2/r och vidare qBr=mv.
Med hjälp av rörelseenergin E=1/2 mv^2 kan vi uttrycka partikelns hastighet v=\sqrt{2E/m}, varvid qBr=m\sqrt{2E/m} eller q^2 B^2 r^2=2mE. För partikelns massa får vi uttrycket
m=\displaystyle{\frac{q^2 B^2 r^2}{2E}}=\frac{(1{,}6\cdot 10^{-19}\, {\rm C})^2 (0{,}0038\, {\rm T})^2 (0{,}045\, {\rm m})^2}{2\cdot 1{,}6\cdot 10^{-19}\cdot 2\,500\, {\rm J}}=9{,}4\cdot 10^{-31}\, {\rm kg}.
Det här motsvarar elektronens massa, alltså är partikeln en positron.
Poängsättning:
7.2 Förklara varför partikeln måste ha färdats i den riktning som pilen visar i bilden och inte i den motsatta riktningen? 4 p.
Krökningsradien för partikelns bana är mindre i bildens övre del. En mindre krökningsradie motsvarar en lägre hastighet. Rörelseenergin eller hastigheten kan inte öka då partikeln tränger igenom plastfilmen, men de kan däremot minska. Färdriktningen måste således vara i enlighet med det som visas i bilden.
Poängsättning:
Typiskt fel:
8. Borneutroninfångningsterapi 15 p.
8.1 Skriv ut reaktionsekvationen med mellansteg för hela kärnreaktionen från neutroninfångning till slutprodukter. 5 p.
Reaktionsekvationen:
^{10}\text{B} + \text{n}\rightarrow {^{11}\text{B}}^{*} \rightarrow { ^7\text{Li}} + { ^4\text{He}} + \gamma
Poängsättning:
8.2 Vid reaktionen frigörs slutligen en alfapartikel, dotternukliden och en gammapartikel. Jämför de olika partiklarnas betydelse för att lokalt förstöra cancercellerna. 6 p.
Alfapartikeln får största delen av den frigjorda kinetiska energin (2,31 MeV), men även ^7Li-kärnan får en del av energin. Räckvidden för dem båda är mycket kort och deras energi absorberas av cancercellen. De frigjorda gammapartiklarna växelverkar svagare med vävnaden och skadar därför även de omgivande friska cellerna.
Poängsättning:
Typiska fel:
8.3 I text sägs det att neutronerna som används vid borneutroninfångningsterapi tidigare har erhållits från kärnreaktorer. Förklara hur neutroner produceras i kärnreaktorer. Hur skiljer sig den nya tekniken från det här? 4 p.
Produktion av neutroner i en kärnreaktor grundar sig på att kärnbränslet består av tunga isotoper som enkelt fissioneras, till exempel ^{235}U eller ^{239}Pu. När de absorberar en neutron klyvs de till två eller fler dotternuklider. Samtidigt frigörs fler neutroner som kan upprätthålla kedjereaktionen. I borneutroninfångningsterapi används de här neutronerna som frigörs vid fission. Reaktionernas antal kan regleras med hjälp av en moderator, exempelvis vatten, som saktar ner neutronerna, eller med styrstavar som kan absorbera dem.
I den nya tekniken använder man en partikelaccelerator och ett strålningsmål som är gjort av litium, alltså ett lätt grundämne. Partikelacceleratorn accelererar protoner mot målet. Isotoperna som uppstår på det här sättet producerar fria neutroner när de sönderfaller. För att reaktionerna ska ske krävs det energi som kommer från partikelacceleratorn. Reaktionerna upphör när partikelstrålen stängs av.
Poängsättning:
Del 3: 20-poängsuppgifter
9. Energiproduktion på ett majsfält 20 p.
9.1
Den årliga energimängden per ytenhet som når ett majsfält från solen är i medeltal 1,46 MWh/m2.
Beräkna den maximala verkningsgraden för energiproduktion från bioetanol (med andra ord förhållandet mellan energin som kan utnyttjas och energin som kommer från solen) om högst 44 % av den energi som frigörs från etanol kan utnyttjas.
6 p.
Medelskörden från majsodlingen är s_m=7\,980\; {\rm kg/ha} = 0{,}7980\; {\rm kg/m^2} och densiteten för etanol är \rho_e=790\; {\rm kg/m^2}=0{,}790\; {\rm kg/l}. Massan av etanol som produceras på fältet per ytenhet är
m_e= s_m \varepsilon_e \rho_e=0{,}262885\; {\rm kg/m^2},
där \varepsilon_e=0{,}417\; {\rm l/kg} är mängden etanol som produceras från varje kilogram av majs. Mängden energi som kan utnyttjas från den producerade etanolen är per ytenhet
E_e= m_e H_e \eta_e= s_m \varepsilon_e \rho_e H_e \eta_e=3\,111{,}51\; {\rm kJ/m^2},
där H_e=26{,}9\; {\rm MJ/kg} är värmevärdet för etanol och \eta_e=0{,}44 är verkningsgraden för en förbränningsmotor som drivs med etanol. Den totala årliga energin per ytenhet från solens strålning är
E_a=1{,}46\; {\rm MWh/m^2} \cdot 3\,600\; {\rm s/h}=5\,256\,000\; {\rm kJ/m^2}.
Energiproduktionens maximala verkningsgrad är då
\eta=\displaystyle{\frac{E_e}{E_a}} =\frac{s_m \varepsilon_e \rho_e H_e \eta_e}{E_a} =0{,}000591992 \approx 5{,}9 \cdot 10^{-4}.
Poängsättning:
Typiskt fel:
9.2
Både odling av majs och den egentliga produktionen av etanol kräver en liten mängd energi utöver den energi som kommer från solen. Det här är den så kallade processenergin. Processens avkastning beskriver förhållandet mellan mängden nettoenergi som fås ur processen och processenergin, där nettoenergin är skillnaden mellan den producerade energin och processenergin.
Beräkna avkastningen i procent för den energi från bioetanol som kan utnyttjas om odlingen och produktionen av etanol krävt 7460 kJ processenergi för varje liter etanol.
5 p.
Avkastningen beskriver hur många gånger mer energi man får ur processen i jämförelse med processenergin, alltså är avkastningen
y=\displaystyle{\frac{E_e-E_p}{E_p}} ,
där E_e är energin per ytenhet som man får ur etanol och E_p är processenergin per ytenhet.
Mängden energi man får ur etanolen är densamma som i deluppgift 9.1, alltså E_e= s_m \varepsilon_e \rho_e H_e \eta_e=3\,111{,}51\ \mathrm{kJ/m^2}. Processenergin som behövs för produktion av en liter etanol är E_l=7\,460\ \mathrm{kJ/l}.
Processenergin per ytenhet blir då
E_p=E_l s_m \varepsilon_e=2\,482{,}43\, {\rm kJ/m^2},
där s_m är medelskörden per ytenhet för majs och \varepsilon_e är etanolproduktionen från majs.
Ur det här följer att avkastningen är
y=\displaystyle{\frac{E_e-E_p}{E_p}} = \frac{s_m \varepsilon_e \rho_e H_e \eta_e}{E_l s_m \varepsilon_e }-1=\frac{\rho_e H_e \eta_e}{E_l} -1=0{,}253410 \approx 25\, \%.
Pisteitys:
Typiskt fel:
9.3
Förutom energiproduktionen som utgår ifrån bioetanol kan även bioavfallet från majsodlingen utnyttjas genom förbränning i fjärrvärmekraftverk. Där kan 85 % av energiinnehållet från avfallet tas till vara. Alternativt skulle solpaneler kunna installeras på majsfältet istället för odlingar. Med hjälp av solpaneler är det möjligt att utnyttja 18 % av energin från solens strålning.
Hur många gånger mera solenergi från solpaneler än utnyttjbar bioenergi från majsodling kan man få från samma fält?
4 p.
När fjärrvärmen som fås från bioavfallet räknas med blir den totala årliga produktionen av bioenergi per ytenhet
E_b=E_e+E_j=s_m \varepsilon_e \rho_e H_e \eta_e+ s_j H_j \eta_j,
där s_j=7\,500\,{\rm kg/ha}=0{,}7500 kg/m^2 är den genomsnittliga massan av bioavfall per ytenhet, H_j=19{,}0 MJ/kg är avfallets värmevärde och \eta_j=0{,}85 är verkningsgraden för fjärrvärmeproduktionen.
Mängden energi man får ur etanolen är densamma som i deluppgift 9.1, alltså E_e= s_m \varepsilon_e \rho_e H_e \eta_e=3\,111{,}51\ \mathrm{kJ/m^2}, och energin som utvinns ur bioavfallet är E_j= s_j H_j \eta_j=12\,112{,}5\ \mathrm{kJ/m^2}.
Den totala bioenergin kan jämföras med solenergin, vilken är 18 % av den totala energin från solens strålning (E_a=5\,256\,000 \mathrm{kJ/m^2}, från deluppgift 9.1). Mängden solenergi i förhållande till den totala bioenergin är
n=\displaystyle{\frac{0{,}18\cdot E_a}{E_e+E_j}}= \frac{0{,}18\cdot E_a}{s_m \varepsilon_e \rho_e H_e \eta_e+ s_j H_j \eta_j }=62{,}1439 \approx 62.
Mängden solenergi är alltså 62 gånger så stor som den totala mängden bioenergi.
Poängsättning:
Typiska fel:
9.4
Med en förbränningsmotor i en etanolbil kan bara 44 % av den frigjorda energin från etanol utnyttjas. För en etanolbil blir dock räckvidden tillräcklig redan med en 65 liters bränsletank. Elmotorn i en elbil kan däremot utnyttja så mycket som 89 % av energin som är lagrad i batterierna, men energitätheten hos batteriet i en elbil är endast ungefär 150 Wh/kg.
Vilken massa bör batteriet i en elbil ha för att en fulladdad elbil och en fulltankad etanolbil ska ha lika stor mängd utnyttjbar energi?
5 p.
Ur etanolen i etanolbilens bränsletank får vi följande mängd energi
E_{ea}= m_e H_e \eta_e=V\rho_e H_e \eta_e,
där V=65\, {\rm l} är volymen av etanol, \rho_e är etanolens densitet, H_e är etanolens värmevärde och \eta_e är verkningsgraden för en förbränningsmotor som drivs med etanol.
Mängden energi som kan utnyttjas i en elbil är
E_{sa}=m_a \omega_a \eta_s,
där m_a är massan för elbilens batteri, \omega_a är batteriets energitäthet och \eta_s är verkningsgraden för elmotorn.
Batteriets energitäthet är \omega_a=150\, {\rm Wh/kg}=540\ \mathrm{kJ/kg}.
Om den utnyttjbara energimängden i båda bilarna är lika stor, alltså E_{ea}=E_{sa} får vi ekvationen
V\rho_e H_e \eta_e=m_a \omega_a \eta_s.
Massan för elbilens batteri blir då
m_a=\displaystyle{\frac{V\rho_e H_e \eta_e}{\omega_a \eta_s }}=\frac{65\, {\rm l} \cdot 0{,}790\,{\rm kg/l}\cdot 26\,900\,{\rm kJ/kg} \cdot 0{,}44}{540\,{\rm kJ/kg} \cdot 0{,}89}=1\,264{,}62\,{\rm kg} \approx 1\,300\,{\rm kg}.
Poängsättning:
Typiskt fel:
10. En rullande cylinder 20 p.
10.1 Rita en bild av krafterna som påverkar cylindern i situationen i bild . 4 p.
Cylindern påverkas av tre krafter: tyngden {\vec G}, underlagets stödkraft {\vec N} och friktion {\vec F}_{\mu}.
Poängsättning:
Typiska fel:
10.2 Är friktionen som påverkar cylindern glid- eller vilofriktion? 2 p.
Cylindern rullar utan att glida, alltså punkten (egentligen segmentet) på cylindern som rör planet glider inte i förhållande till planet. Det är alltså fråga om vilofriktion.
Poängsättning:
10.3 Material visar vilken stödkraft som påverkar cylindern enligt vad som bestämts genom simulering. Varför har stödkraften lokala maximi- och minimivärden? 5 p.
Vi undersöker rörelsen för cylinderns massmedelpunkt i riktningen av planets normal. Massmedelpunktens avstånd från planet varierar periodiskt, alltså är massmedelpunkten i accelererad rörelse och enligt Newtons andra lag påverkas den i riktningen av planets normal av en total kraft som avviker från noll. Tyngden som påverkar cylindern är konstant, vilket betyder att stödkraften måste variera periodiskt för att accelerationen ska variera periodiskt. För varje varv har stödkraften ett lokalt maximum, när accelerationen för cylinderns massmedelpunkt uppnår sitt maximivärde, alltså massmedelpunktens hastighet bort från planet ökar som kraftigast. Ett lokalt minimivärde uppstår då accelerationen uppnår sitt minimivärde, alltså när massmedelpunktens hastighet mot planet ökar som kraftigast.
Poängsättning:
10.4 I video märker vi att cylindern i något skede frigör sig från underlaget. Bestäm tidpunkten vid vilken detta sker utgående från materialet . 4 p.
Cylindern frigör sig från underlaget när stödkraftens minimivärde uppnår noll. Det här kan observeras i bild 10.C vid tidpunkten 1,91 s eller 1,99 s (båda godkänns).
Poängsättning:
10.5 Tabell anger massmedelpunktens hastighet i planets riktning som funktion av tiden. Använd en lämplig grafisk framställning för att bestämma värdet som accelerationen för cylinderns massmedelpunkt i planets riktning närmar sig när rörelsen fortskrider. 5 p.
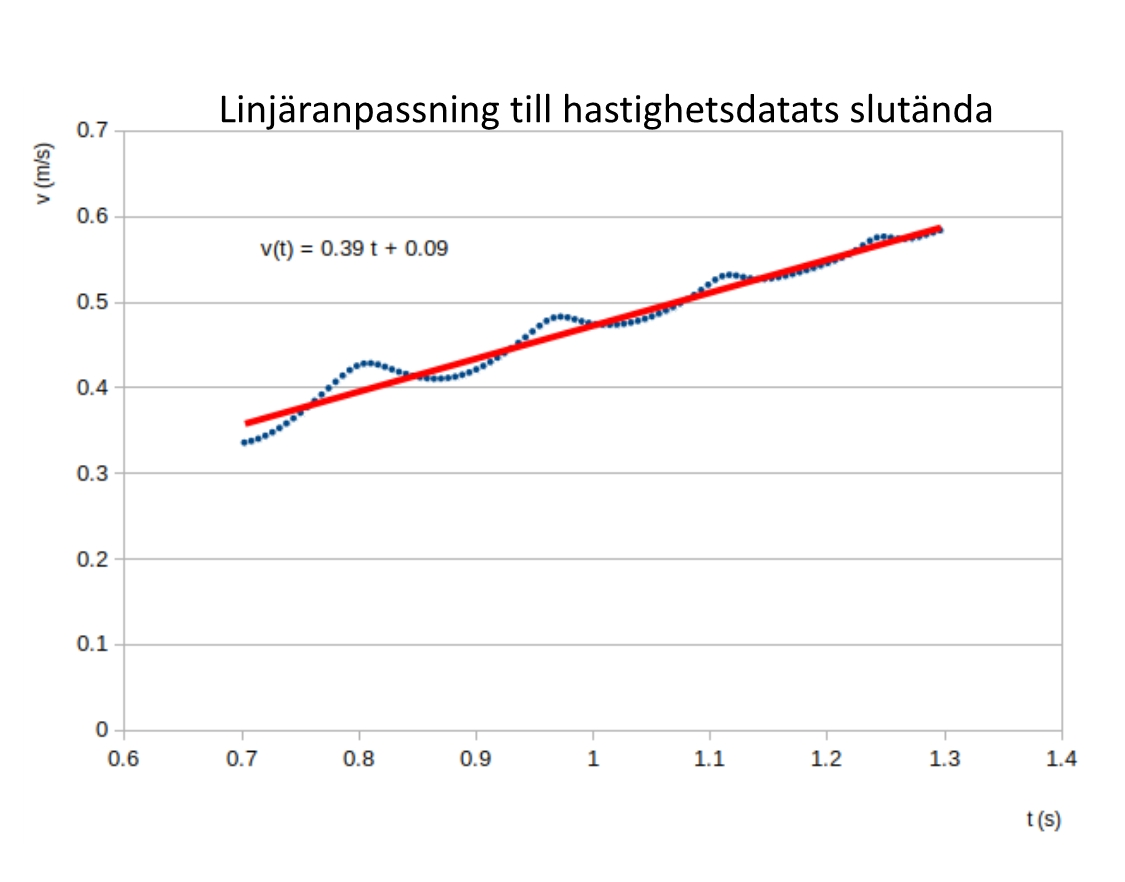
Efter det här gör vi en linjär anpassning till slutet av hastighetsdata, och från riktningskoefficienten får vi accelerationens medelvärde
\displaystyle{\frac{\Delta v}{\Delta t}}\approx 0{,}39\, \frac{m}{s^2}.
Accelerationen närmar sig det här värdet då fluktuationerna i hastigheten avtar när rörelsen framskrider.
Alternativt ritar vi en linjär kuvertkurva som kopplar samman de lokala maximumen eller minimumen (det första minimumet utelämnas). Medeltalet av kuvertkurvornas riktningskoefficienter ger oss också 0,39 m/s^2.
Poängsättning:
11. Värmestrålning från jordytan 20 p.
11.1 I intensitetsfördelningen kan man urskilja tydliga gropar vid punkterna A och B. Vilket är våglängdsintervallet som motsvaras av gropen vid punkten A? Vad förorsakar dessa gropar i intensitetsfördelningen? 6 p.
På bilden ser vi att grop A börjar vid punkten (1/\lambda)_{\rm min}\approx 570\,{\rm cm}^{-1} och slutar vid punkten (1/\lambda)_{\rm max}\approx 770\,{\rm cm}^{-1}. De motsvarande våglängderna är \lambda_{\rm min}=(1/770)\,{\rm cm}\approx 13\,\mu {\rm m} och \lambda_{\rm max}=(1/570)\,{\rm cm}\approx 18\,\mu {\rm m}.
Våglängdsintervallet för grop A är alltså ungefär 13–18 \,\mu {\rm m}.
Den avsaknad av intensitet som motsvaras av groparna orsakas av absorption av värmestrålning från jorden i atmosfärens gaser.
Poängsättning:
11.2
Ett strålningsspektrum från en svartkropp har anpassats till de uppmätta data. Vad är jordens yttemperatur enligt anpassningen? Använd dig av Wiens förskjutningslag som här presenteras i förhållande till frekvensen:
f_{\rm max}=\frac{\alpha}{h}k\,T,
där h är Plancks konstant, k är Boltzmanns konstant och α ≈ 2,8214.
8 p.
Wiens förskjutningslag beskriver hur maximivärdet i intensitetsfördelningen beror av den strålande kroppens temperatur. I den givna Wiens förskjutningslag är f_{\max} frekvensen där intensiteten är maximal. Den här frekvensen kan beräknas från vågtalet som ger den högsta intensiteten. Enligt anpassningen är (1/\lambda)_{\rm max}\approx 580\,{\rm cm}^{-1}. Ur vågrörelsens grundekvation får vi
f_{\rm max}=c\left(\displaystyle{\frac{1}{\lambda}}\right)_{\rm max}.
Wiens förskjutningslag kan nu skrivas i formen
c\left(\displaystyle{\frac{1}{\lambda}}\right)_{\rm max}=\displaystyle{\frac{\alpha}{h}}k\,T,
ur vilket vi får en storhetsekvation för temperaturen
T=\displaystyle{\frac{c\,h}{\alpha\,k}}\left(\frac{1}{\lambda}\right)_{\rm max}.
Genom att substituera siffervärden i ekvationen får vi
T=\displaystyle{\frac{2{,}9979\times 10^{8}\,{\rm m/s}\cdot 6{,}6261\times 10^{-34} {\rm Js}}{2{,}8214\cdot 1{,}3806 \times 10^{-23}\,{\rm m}^2\,{\rm kg}\,{\rm s}^{-2}\,{\rm K}^{-1}}}\cdot 580\times 10^2\,{\rm m}^{-1}\approx 296\,{\rm K} \approx 22{,}6^{\circ}{\rm C}.
Jordens yttemperatur är ungefär 300 \mathrm{K} (ungefär 23\ ^{\circ}{\rm C}).
Poängsättning:
Typiskt fel:
11.3 I bild syns den lokala fördelningen av värmestrålningens intensitet på jordklotet, uppmätt i övre delen av atmosfären. Fördelningen ger ett medeltal från åren 2003–2011. Förklara kortfattat vilka faktorer som påverkar de lokala variationerna i strålningen. 6 p.
De lokala fluktuationerna i värmestrålningen som uppmätts i övre atmosfären är i första hand beroende av temperaturskillnader mellan olika regioner. Solens strålning är i genomsnitt riktad mera mot områdena omkring ekvatorn, och dess intensitet minskar i och med ökande breddgrader. Därför är exempelvis polarområdena svala och avger mindre värmestrålning än områdena nära ekvatorn.
En annan betydande faktor är växlingarna i molntäcket. Exempelvis runt ekvatorn är det i genomsnitt betydligt molnigare än vid ökenområden som till exempel Sahara och Mellanöstern. I molniga områden framhävs absorption av långvågig värmestrålning i vattenånga, vilket minskar på värmestrålningen som uppmäts i den övre atmosfären.
Poängsättning:
Typiskt fel: