Hyvän vastauksen piirteet: FI – Matematiikka, pitkä oppimäärä
22.3.2023
Lopulliset hyvän vastauksen piirteet 16.5.2023
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.
Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.
Miten pisteytysohjeita luetaan
- Ohjeen rakenne
- Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy oikeassa sarakkeessa olevaan pistemäärään.
- Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
- Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
- Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
- Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esim. derivaatan laskeminen osittain oikein).
- Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
- Suluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
- Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37{,}5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
- Rivien riippuvuus toisistaan
- Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esim. laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
- Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
- Merkintä ylläolevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
- Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
- Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
- Terminologiaa
- ''Vastaus riittää'' tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
- ''Alkupisteitä'' tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
- ''maxN'' tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
- ''Vastaus vain likiarvona'' tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.
- Vastaus oikein, muttei pyydetyssä muodossa (esim. tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esim. e^1, \ln(e) tai 4^0) -2 p.
- Vastaus sieventämättä muussa tehtävässä (esim. e^1, \ln(e) tai 4^0) -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esim. x=2, y04), tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.
- Matemaattisesti puutteellinen merkintä (esim. puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
Kolmisarakkeisen lukuohjeet:
- Ideasarakkeesta saa pisteet, jos on ryhdytty tekemään mainittua asiaa, vaikka toteutus olisi puutteellinen.
- Lasku tai kaava toteutussarakkeessa näyttää, miltä idea oikein toteutettuna näyttää.
- Pysäytysehto: jokaiselta riviltä saatava vähintään puolet rivin pisteistä pyöristettynä alaspäin, jotta voi jatkaa.
- Jos pysäytysehto ei toteudu, eli seuraavien rivien pisteitä on vielä jaossa, on seuraavilta riveiltä saatavissa kaikki pisteet, joissa ei ole eksplisiittistä estettä sille, miksi niitä ei voisi saada.
A-osa
1. Monivalintatehtävä 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 Mittayksiköt 2 p.
- 10^{6} (2 p.)
1.2 Lieriö 2 p.
- särmiö (2 p.)
1.3 Kosinilause 2 p.
- Pythagoraan lause (2 p.)
1.4 Kulmakerroin 2 p.
- yhtälöstä muodostetun funktion f(x)=ax+b derivaatan arvo (2 p.)
1.5 Pistetulo 2 p.
- Virheellinen vastaus, joka antaa pisteitä: kokonaisluku (1 p.)
- reaaliluku (2 p.)
1.6 Leikkauspisteet 2 p.
- korkeintaan neljä leikkauspistettä (2 p.)
2. Yhdistely 12 p.
Alla on annettu 12 yhtälöä. Yhdeksää niistä vastaa jokin kuvassa annetuista kuvaajista. Yhdistä kukin yhtälö sitä vastaavaan kuvaajaan tai merkitse, että sellaista ei ole.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 1 p., väärä vastaus 0 p., ei vastausta 0 p.
2.1 1 p.
- Kuvaaja 9 (1 p.)
2.2 1 p.
- Kuvaaja 2 (1 p.)
2.3 1 p.
- Ei kuvaajaa (1 p.)
2.4 1 p.
- Kuvaaja 12 (1 p.)
2.5 1 p.
- Kuvaaja 4 (1 p.)
2.6 1 p.
- Kuvaaja 5 (1 p.)
2.7 1 p.
- Kuvaaja 7 (1 p.)
2.8 1 p.
- Kuvaaja 1 (1 p.)
2.9 1 p.
- Kuvaaja 10 (1 p.)
2.10 1 p.
- Ei kuvaajaa (1 p.)
2.11 1 p.
- Kuvaaja 3 (1 p.)
2.12 1 p.
- Ei kuvaajaa (1 p.)
3. Ratakisko 12 p.
Kymmenen metriä pitkä museoratakisko on vääntynyt lämpölaajenemisen vuoksi mutkalle, mutta sen päät ovat pysyneet paikoillaan (katso liioiteltu kuva tilanteesta). Kiskon poikkeama sen alkuperäisestä sijainnista kohtisuoraan mitattuna on muotoa
f(x)=\frac{x^3-15x^2+50x}{1000},
kun x on etäisyys kiskon alkupäästä. Missä kohdissa kiskon poikkeama sen alkuperäisestä asemasta on suurin? Määritä myös suurin poikkeama. Muuttujan x ja poikkeaman yksikkönä on metri.
| Laskettu funktion derivaatta f'(x)=\frac{1}{1000}(3x^2-30x+50). | 2 p. |
| Jos derivaatta ei ole toisen asteen polynomi, vain riippumaton -rivin pisteet jaossa jatkossa. | |
| Derivaatan nollakohdat (likiarvot riittävällä tarkkuudella käyvät) x=\frac{30\pm 10\sqrt{3}}{2\cdot 3}=5\pm \frac{5}{\sqrt{3}} (2{,}1132\ldots ja 7{,}8867\ldots). | 2 p. |
| Funktion arvon laskeminen välille ]0,10[ kuuluvissa derivaatan nollakohdissa. | 1+1 p. |
| riippumaton Todettu, että suurimmat poikkeamat ovat derivaatan nollakohdissa. Perusteltu tämä jotenkin (esimerkiksi kuva tai kulkukaavio ilman rajoitusta välille). | 2 p. |
| Vertailtu poikkeamia derivaatan nollakohdissa, jotka ovat välillä ]0,10[. | (1 p.) |
| Annettu vastaukset likiarvoina 2\mathrm{,}11 (m) ja 7\mathrm{,}89 (m) ja poikkeama 0\mathrm{,}048 (m), poikkeamakohtien oltava välillä ]0,10[. | 3 p. |
| Tämän ratkaisun erillisohjeet | |
| Ratkaisussa voi tarkastella myös pelkkää osoittajan derivaattaa. | |
| Vastauksessa annettu negatiivinen poikkeama -0{,}048. | max 12 p. |
| Derivoinnissa virhe ja derivaatta 2. asteen polynomi (1+2+2+2+2+2). | max 11 p. |
| Derivaatan nollakohdissa virhe, jonka seurauksena vain yksi derivaatan nollakohta tarkasteluvälillä (2+1+1+2+0+2). | max 8 p. |
| Vedottu symmetriaan kohdan x=5 suhteen ja laskettu vain toinen poikkeamista (2+2+1+2+1+3). | max 11 p. |
| Tulkittu suurin poikkeama suurimmaksi arvoksi ja funktion arvoa f(7{,}88\ldots) ei ole laskettu (2+2+1+2+0+2). | max 9 p. |
| TAI Kokeilu- tai ohjelmointiratkaisu. | |
| Näytetty kolmen pisteen avulla molemmille huipuille, että keskimmäisessä saadaan suurin/pienin arvo, pisteiden etäisyys enintään kymmenesosa (esimerkiksi 2\mathrm{,}0; 2\mathrm{,}1 ja 2\mathrm{,}2 ja vastaavasti toiselle). | 1+1 p. |
| riippumaton Päätelty huippujen x-koordinaatit merkitsevien numeroiden osalta oikein (esimerkiksi kohtien 2\mathrm{,}0; 2\mathrm{,}1 ja 2\mathrm{,}2 arvoilla päätelty x:n arvoksi noin 2). | 1+1 p. |
| Vertailtu poikkeamia huipuissa. | 1 p. |
| Annettu poikkeama 0\mathrm{,}048 m ja poikkeamaa laskettaessa poikkeamakohdissa ollut vähintään yksi merkitsevä numero enemmän kuin vastauksessa. | 1 p. |
| Annettu poikkeamakohdat likiarvoilla 2\mathrm{,}11 m ja 7\mathrm{,}89 m oikein perustein. | 2 p. |
| riippumaton f(0)=0 ja f(10)=0 TAI päätepisteet pysyvät paikallaan TAI rajoituttu suljetulle välille [0,10]. | 1 p. |
| Perustelu, miksi muita paikallisia ääriarvokohtia ei ole (esimerkiksi kolmannen asteen polynomilla on korkeintaan kaksi paikallista ääriarvokohtaa). | 3 p. |
| Tämän ratkaisun erillisohjeet | |
| Laskettu testipisteillä 2\mathrm{,}10; 2\mathrm{,}11 ja 2\mathrm{,}12, ja päätelty huipun virheellisesti olevan kohdassa 2\mathrm{,}11 ja symmetrisesti toisessa kohdassa, ja annettu poikkeamaksi 0\mathrm{,}048 tai 0\mathrm{,}05 (2+0+1+1+0+1+3). | max 8 p. |
| Kokeiluratkaisu, jossa ei ole käytetty kolmea järkevää testipistettä huipun löytämiseksi (esimerkiksi laskettu poikkeama vain arvoilla 2\mathrm{,}11 ja 2\mathrm{,}12) (0+0+0+0+0+1+0). | max 1 p. |
| Vedottu kuvaajan symmetriaan ja väitetty virheellisesti, että poikkeamakohdat ovat 2\mathrm{,}5 ja 7\mathrm{,}5 (0+0+0+0+0+1+0). | max 1 p. |
| Alkupiste: Laskettu funktion arvot kahdessa välin [0, 10] pisteessä. | 1 p. |
4. Suoran etäisyys kahdesta pisteestä 12 p.
Määritä kaikki suorat, joiden etäisyys pisteestä A=(-2,0) on 2 ja etäisyys pisteestä B=(3,0) on 3.
| Ideasarake | Toteutussarake | Pisteet |
| riippumaton Suora x=0 TAI y-akseli toteuttaa selvästi tehtävänannon ehdot. | 0+1 p. | ||
| Haettu suora sivuaa ympyröitä ja on kohtisuorassa ympyröiden säteitä vastaan TAI vastaavat ehdot muotoiltu toisin (esimerkiksi ilman ympyröitä). | 2+0 p. | ||
| Jotkin järkevät suorakulmaiset kolmiot / yhdenmuotoisuus järkeviin kolmioihin x-akselin leikkauspisteen ratkaisemiseksi. | (Suorakulmainen kolmio, kärjet B=(3, 0), suoran ja isomman ympyrän sivuamispiste P ja suoran ja x-akselin leikkauspiste Q.) Saadaan verranto oikeanlaisesta kolmiosta: \frac{3}{5+z}=\frac{2}{z}, missä z on pisteiden (-2,0) ja Q etäisyys. Siispä z=10. Suora leikkaa x-akselin siis pisteessä (-12, 0). | [1+1] +[1+1] p. | |
| Määritetään k jonkin järkevän kolmion kautta. | Kulmakertoimeen laskemiseen tarvittavat tiedot (esimerkiksi kateetit) ja suoran kulmakerroin k=\frac{h}{15}=\frac{1}{\sqrt{24}}. | 0+3 p. | |
| Suoran yhtälö on y=\frac{1}{\sqrt{24}}(x+12), ja x-akselin alapuolella kulkevan suoran yhtälö on vastaavasti y=-\frac{1}{\sqrt{24}}(x+12). | 0+[1+1] p. | ||
| riippumaton Suora x=0 TAI y-akseli toteuttaa selvästi tehtävänannon ehdot. | 0+1 p. | ||
| Kun liikutaan 5 yksikköä x-akselilla vasemmalle, etäisyys suoraan vähenee kolmesta kahteen. | Liikuttaessa toiset kaksi viiden yksikön matkaa etäisyys vähenee nollaan, jolloin suora leikkaa x-akselin kohdassa x=-12. | 1+[1+1] p. | |
| Idea siitä, että haetut suorat sivuavat ympyröitä ja että suorat ovat kohtisuorassa ympyröiden säteisiin nähden. | Määritetään nyt muut suorat. Näitä on kaksi, ja ne ovat x-akselin suhteen symmetriset. Toinen sivuaa ympyröitä (x-3)^2+y^2=3^2 ja (x+2)^2+y^2=2^2 yläpuolelta ja toinen alapuolelta. | [1+1]+0 p. | |
| Piirretään jokin tilanteen kannalta järkevä suorakulmainen kolmio. | Kulmakertoimen määrää esimerkiksi suorakulmainen kolmio, jonka hypotenuusan pituus on 10 ja vastakkainen kateetti 2. Siten lähemmän kateetin pituus on \sqrt{96}, ja kulmakerroin on \frac{2}{\sqrt{96}} = \frac{1}{\sqrt{24}}. | 1+3 p. | |
| Suoran yhtälö on y=\frac{1}{\sqrt{24}}(x+12), ja x-akselin alapuolella kulkevan suoran yhtälö on vastaavasti y=-\frac{1}{\sqrt{24}}(x+12). | 0+[1+1] p. | ||
| riippumaton Suora x=0 TAI y-akseli toteuttaa selvästi tehtävänannon ehdot. | 0+1 p. | ||
| Käytetään pisteen etäisyys suorasta -kaavaa järkevästi (sijoitettu etäisyys ja piste jotenkin). | Kaksi yhtälöä: \dfrac{|-2a+c|}{\sqrt{a^2+b^2}}=2, \dfrac{|3a+c|}{\sqrt{a^2+b^2}}=3 TAI \dfrac{|-2k+b|}{\sqrt{k^2+1}}=2, \dfrac{|3k+b|}{\sqrt{k^2+1}}=3 | 1+1 p. | |
| Pyritään kahden muuttujan yhtälöön (järkevä aloitus) TAI yhtälöparissa alunperinkin vain kaksi muuttujaa. | Esimerkiksi \dfrac{|-2a+c|}{2}=\dfrac{|3a+c|}{3} TAI \dfrac{|-2k+b|}{2}=\dfrac{|3k+b|}{3} TAI b^2=4+4kb=9-6kb | 1+2 p. | |
| Pyritään ratkaisemaan yksi muuttujista toisen avulla. | c=0 tai c=12a TAI b=12k tai b=0 TAI b=\frac{1}{2k} | 1+1 p. | |
| Sijoitetaan takaisin alkuperäiseen yhtälöön ja ratkaistaan jokin muuttujista. | b=\pm 2\sqrt{6}\,a TAI b=\pm\sqrt{6},\ k=\pm\dfrac{1}{2\sqrt{6}} | 1+1 p. | |
| Suorien yhtälöt ovat y=\frac{1}{2\sqrt{6}}x+\sqrt{6} ja y=-\frac{1}{2\sqrt{6}}x-\sqrt{6}. | 0+[1+1] p. | ||
| Tehtävän erillisohjeet | |||
| Likiarvot tai kulmakerroin trigonometristen funktioiden avulla: viimeisen rivin pisteet jäävät pois (k=0{,}20412\dots, b=2{,}44948\dots). | |||
B1-osa
5. Taikaneliö 12 p.
Kuparikaiverrus Melankolia I (katso kuva ) on saksalaisen Albrecht Dürerin tunnetuimpia teoksia. Teos sisältää 4\times 4 -taikaneliön, jossa jokaisen vaaka- ja pystyrivin lukujen summa on 34. Alla olevassa ruudukossa neljä taikaneliön ruutua on esitetty kahden tuntemattoman luvun x ja y avulla. Kun luvut x ja y asetetaan peräkkäin, saadaan tuloksena teoksen valmistumisvuosi. Ratkaise luvut x ja y ja kirjoita kyseessä oleva vuosiluku.
\begin{array}{|c|c|c|c|} \hline 16 & 3 & 2 & 13\\ \hline 5 & 10 & 11 & 8\\ \hline 9 & \frac{y-2}2 & \frac{x-1}2 & 12\\ \hline 4 & x & y & 1\\ \hline \end{array}
| Viimeiseltä vaakariviltä ja kolmannelta pystyriviltä saadaan yhtälöt 4+x+y+1=34 ja 2+11+\frac{x-1}{2}+y=34. | 3+3 p. |
| Ratkaisemalla yhtälöpari (esim. solve-komennolla) saadaan luvuiksi x=15 ja y=14 (oikea aloitus / toinen muuttuja ratkaistu toisen avulla / molemmat ratkaistu). | 1+1+1 p. |
| Kysytty vuosiluku on siis 1514 TAI 1415. | 1 p. |
| Tarkistetaan vielä, että nämä todella toteuttavat loput kaksi yhtälöä: kolmas vaakarivi: 9+\frac{14-2}{2}+\frac{15-1}{2}+12=34 sekä toinen pystyrivi: 3+10+\frac{14-2}{2}+15=34. | 1+1 p. |
| Tämän ratkaisun erillisohjeet | |
| Ensimmäisellä pisterivillä ensimmäisestä yhtälöstä 3 p. ja toisesta tämän kanssa lineaarisesti riippumattomasta 3 p. | |
| Yhtälöryhmä oikein, vastaus ilman mainintaa yhtälöryhmän ratkaisusta: yleisvähennys -1 p. | |
| TAI | |
| Testattu (neljä kertaa), että valinnoilla x=15 ja y=14 rivi- tai sarakesummaksi tulee 34. | 2*4 p. |
| Vähintään kaksi lineaarisesti riippumatonta testausta ja vastaus 1514 TAI 1415. | 1 p. |
| Perusteltu yksikäsitteisyys. | 3 p. |
| Tämän ratkaisun erillisohjeet | |
| Testattu joillakin muilla luvuilla, ensimmäisestä täytetystä ehdosta: | 2 p. |
| Käytetty lävistäjien summaa ehtona, 2 p. kummastakin yhtälöstä ja 1 p. vastauksesta. (Jos on lisäksi vaaka- ja pystyriviehtojen tarkistus, pisteytys jälkimmäisen ohjeen mukaan ilman lisäpisteitä lävistäjäehdosta.) | 5 p. |
6. Raketin nokkakartio 12 p.
Erään raketin kärki, eli niin sanottu nokkakartio, saadaan, kun alaspäin aukeava paraabeli pyörähtää symmetria-akselinsa ympäri. Kärjen korkeus on 4,5 metriä, ja sen halkaisija pohjan tasolla on 3,3 metriä. Määritä kärjen tilavuus.
| Ratkaisun alku: Paraabelin konstruktio | |
| Mallinnetaan aluksi poikkileikkausparaabeli. Asetetaan se koordinaatistoon niin, että sen nollakohdat ovat pisteissä x=\pm\frac{3\mathrm{,}3}{2}=\pm 1\mathrm{,}65\ (=\frac{33}{20}). | (2 p.) |
| Paraabelin yhtälö on siis y=a(x-1\mathrm{,}65)(x+1\mathrm{,}65). | 2 p. |
| Poikkileikkauksen korkeus on paraabelin y-koordinaatti siinä pisteessä, jossa paraabeli leikkaa y-akselin. Tämä saadaan siis yhtälöstä 4\mathrm{,}5=-a\cdot 1\mathrm{,}65^2, eli a=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}\ (=-\frac{200}{121}). | 2 p. |
| Paraabeliksi on siis saatu y=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}\left(x^2-1\mathrm{,}65^2\right)\ (=-\frac{200}{121}x^2+\frac{9}{2}), | 1 p. |
| TAI (ratkaisun alku toisin) | |
| Mallinnetaan aluksi poikkileikkausparaabeli. Asetetaan se koordinaatistoon niin, että se aukeaa alaspäin ja sen huippu osuus pisteeseen (0;\ 4{,}5). | (2 p.) |
| Paraabelin yhtälö on siis y=4{,}5+a(x-0)^2 TAI y=4{,}5+ax^2 TAI ekvivalentti muotoilu. | 2 p. |
| Sijoitetaan jompi kumpi paraabelin nollakohdista x=\pm1{,}65 yhtälöön ja saadaan -4{,}5=a(1{,}65)^2 eli a = -4{,}5/(1{,}65^2). | 2 p. |
| Paraabeliksi on siis saatu y=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}x^2+4{,}5, | 1 p. |
| Ratkaisun loppu: Integraalin laskeminen | |
| josta x=\pm \sqrt{-\frac{1\mathrm{,}65^2}{4\mathrm{,}5}y+1\mathrm{,65}^2}. | 1 p. |
| Tilavuus saadaan nyt pyörähdyskappaleen integraalina \pi \int_0^{4\mathrm{,}5}\left(-\frac{1\mathrm{,}65^2}{4\mathrm{,}5}y+1\mathrm{,65^2}\right)\mathrm{d}y | 2 p. |
| \approx 19\mathrm{,}2442\approx 19 (kuutiometriä). | 2 p. |
| Tämän ratkaisun erillisohjeet | |
| Huomaa, että a=-\frac{200}{121}=-1{,}652... on lähellä lukua -1{,}65. Jos a=\frac{3{,}3}{2}, vakion a arvo ilmestyy tyhjästä tai se on muuten selvästi väärä, niin (2+2+0+0+1+2+2). Ei koske niitä huolimattomuusvirheitä, joissa ajatus on oikea. | max 9 p. |
| Integroinnissa toiseksi viimeisellä rivillä voi mennä useita asioita väärin. Tässä on esimerkkejä kahden viimeisen rivin pisteistä: | |
| Toiseksi viimeisen rivin integraalista puuttuu \pi, mutta se on muuten oikein. | max 3 p. |
| Integroitava lauseke on x^2:n sijaan x. | max 1 p. |
| Täysin väärä tilavuus (esimerkiksi paraabeli pyöräytetty väärän akselin ympäri). | 0 p. |
| TAI | |
| Paraabelin kertoimille kolmen yhtälön yhtälöryhmä (1 p./oikea yhtälö). | 3 p. |
| Saatu oman paraabelin kertoimet (1 oikein 1 p, 3 oikein 2 p.). | 2 p. |
| Perustelu yhtälöryhmän ratkaisulle (esimerkiksi solve- tai GG-komento). | 1 p. |
| Oikea oma paraabeli (esimerkiksi muodossa y=f(x)), | 1 p. |
| josta ratkaistu x. | 1 p. |
| Tilavuus kirjoitettu pyörähdyskappaleen integraalina. | 2 p. |
| Vastaus \approx 19\mathrm{,}2442\approx 19 (kuutiometriä). | 2 p. |
| TAI | |
| (Nokkakartio on pyörähdysparaboloidi, jonka) tilavuus on \frac{1}{2}\pi r^2h, | 2 p. |
| riippumaton jossa säde r=\frac{3\mathrm{,}3}{2}=1\mathrm{,}65 (metriä) ja korkeus h=4\mathrm{,}5 (metriä). | 2 p. |
| Tilavuus on siis \frac{1}{2}\pi\cdot 1\mathrm{,}65^2\cdot 4\mathrm{,}5 (säde 3 p., korkeus 3 p.) | 6 p. |
| \approx 19\mathrm{,}2442\approx 19 (kuutiometriä). | 2 p. |
| Tämän ratkaisun erillisohjeet | |
| Laskettu tilavuus kartion tilavuuden kaavalla (0+2+0+0). | max 2 p. |
| Laskettu halkaisijan pituudella (2+1+3+2). | max 8 p. |
| Tehtävän erillisohjeet | |
| Paraabeli voidaan asettaa koordinaatistoon eri tavoin, myös vaakasuoraan. |
7. Vektoreiden summa 12 p.
Tarkastellaan vektoreita \overline{u}=\overline{i}+2 \,\overline{j} ja \overline{v} = \sin(2t)\overline{i} + \cos(4t) \overline{j}, missä t \ge 0.
Määritä vektori \overline{u}+\overline{v}, kun t=0, t=\frac\pi 4 ja t=\frac{3\pi}4. (4 p.)
Mikä tasokuvio muodostuu vektorin \overline{u}+\overline{v} kärkipisteestä, kun t saa arvot välillä [0, \pi]? Anna vastaus yhtälönä muodossa y=f(x). Ratkaisussa voi käyttää esimerkiksi kaavaa \cos (2x)=1-2\sin^2 x. (8 p.)
| Sijoitettu joku kolmesta t:n arvosta oikein summan lausekkeeseen. | 1 p. |
| t=0: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin(2\cdot 0)\overline{i}+\cos (4\cdot 0)\overline{j}=\overline{i}+3\overline{j} | 1 p. |
| t=\frac{\pi}{4}: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin\left(2\cdot \frac{\pi}{4}\right)\overline{i}+\cos \left(4\cdot \frac{\pi}{4}\right)\overline{j}=2\overline{i}+\overline{j} | 1 p. |
| t=\frac{3\pi}{4}: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin\left(2\cdot \frac{3\pi}{4}\right)\overline{i}+\cos \left(4\cdot \frac{3\pi}{4}\right)\overline{j}=\overline{j} | 1 p. |
| Osatehtävän erillisohjeet | |
| Vastaukset muodossa 1i+3j, 2i+1j tai 0i+1j. | –0 p. |
| Vastaus eri muodossa, esimerkiksi saatu ohjelmasta vastaukseksi [0\ 1]. | –0 p. |
| Välivaiheissa likiarvoja (esimerkiksi \pi\approx 3{,}14), yhteensä | –1 p. |
| Pelkät vastaukset (esimerkiksi kuvakaappauksina ohjelman tuloksista). | max 2 p. |
| Laskin astemoodissa. | 1+1+0+0 p. |
| Alkupiste: Sievennetty joku kuudesta sin- tai cos-arvosta ilman vektoreita. | 1 p. |
| Esiintyy lausekkeet \sin(2t)+1 ja \cos (4t)+2 (esimerkiksi kertoimina jo 7.1:ssä). | 1 p. |
| Merkitään x=\sin(2t)+1 ja y=\cos (4t)+2. | 1 p. |
| Saadaan käyrä y=\cos (4t)+2=1-2\sin^2(2t)+2=3-2\sin^2(2t)=3-2(x-1)^2 (=1+4x-2x^2) (kaavan käyttö ja x-muoto: 2+2), | 4 p. |
| jossa x saa arvot väliltä [0,2] ja perustelu (ääripäät esimerkiksi valinnoilla t=\frac{3\pi}{4} ja t=\frac{\pi}{4}.) | 2 p. |
| TAI | |
| Esiintyy lausekkeet \sin(2t)+1 ja \cos (4t)+2 (esimerkiksi kertoimina jo 7.1:ssä). | 1 p. |
| Sijoitettu ohjelmaan \sin(2t)+1 ja \cos(4t)+2. | 1 p. |
| Piirretty paraabelin kaari, | 1 p. |
| kun t vaihtelee oikealla välillä. | 1 p. |
| Päätelty paraabelin kertoimet esimerkiksi kolmen pisteen avulla. | 1 p. |
| Lisäperustelut paraabelille. | 3 p. |
| TAI | |
| t=\frac{1}{2}\sin^{-1}(x-1), josta y=\cos(2\sin^{-1}(x-1))+2 välillä [0, 2] ja maininta paraabelista: (1)+2+2+1 | max 6 p. |
8. Polynomien vertailu 12 p.
Osoita induktiolla, että k^3\ge k^2+4 kaikilla kokonaisluvuilla k\ge 2. (6 p.)
Osoita, että osatehtävän 8.1 epäyhtälö ei päde millään kokonaisluvulla k<0. (2 p.)
Osoita, että epäyhtälö x^3\ge x^2+4 pätee kaikilla reaaliluvuilla x\ge 2. (4 p.)
| riippumaton Induktion alkuaskel: Kun k=2, on väitetty epäyhtälö 2^3\geq 2^2+4, eli 8\geq 8, joka on tosi. | 1 p. |
| Induktio-oletus: Oletetaan, että jollakin luvun k\geq 2 arvolla pätee k^3\geq k^2+4. | 1 p. |
| Induktioväite: Väitetään, että (k+1)^3\geq (k+1)^2+4. | 1 p. |
| (k+1)^3=k^3+3k^2+3k+1 | (1) p. |
| Induktioväitteen todistuksessa käytetty induktio-oletusta (vasen puoli k^3+3k^2+3k+1\geq k^2+4+3k^2+3k+1 TAI väite (k^2+4)+3k^2+3k+1 -(k+1)^2 - 4 \ge 0). | 1 p. |
| k^2+4+3k^2+3k+1\geq k^2+2k+1+4=(k+1)^2+4 TAI saatu ehdosta tosi epäyhtälö. | 1 p. |
| Osatehtävän erillisohjeet | |
| Alkupiste: Kokeiltu, että epäyhtälö toteutuu jollakin k \ge 2 arvolla. (Tämä piste saattaa hyvin löytyä myös osatehtävästä 8.2 tai 8.3.) | 1 p. |
| Todistettu induktioväitettä käyttämättä induktio-oletusta: 1+1+1+1+0+0 | max 4 p. |
| Induktio-oletuksessa epäselvää, että kyse on jostakin muuttujan k arvosta tai muu epäselvyys induktion rakenteessa. | –1 p. |
| Induktion terminologian ei tarvitse olla juuri yllä oleva, kunhan rakenne on selvä. | –0 p. |
| Todistettu epäyhtälö käyttämättä induktiota. | +0 p. |
| riippumaton Kun k<0, on k^3<0. | 1 p. |
| riippumaton k^2+4>0 | 1 p. |
| Osatehtävän erillisohjeet | |
| Esimerkki k:n arvosta, jolla ei toimi. | +0 p. |
| Muodostetaan funktio f(x)=x^3-x^2-4 TAI idea kahden funktion derivoinnista. | 1 p. |
| f'(x)=3x^2-2x TAI kahden derivaatan 3x^2 ja 2x vertailu. | 1 p. |
| Osoitettu, että f'(x) \ge 0, kun x \ge 2 (esimerkiksi derivaatan nollakohdat ovat x=0 ja x=\frac{2}{3} ja funktion kulkukaavio on muotoa + | - | + TAI f'(x)=x (3x-2) \ge 0, kun x \ge 2). | 1 p. |
| Kun x\geq 2, on funktio siis kasvava. Koska f(2)=0, väite on todistettu. | 1 p. |
| TAI | |
| Jaetaan luvulla x^2, joka on positiivinen, eli pitää osoittaa x \ge 1+4/x^2. | 2 p. |
| Koska x\ge 2 \ge 1+\frac{4}{x^2}, tämä on selvä. | 2 p. |
| TAI | |
| x^3-x^2 = x^2 (x-1) \ge 4, kun x \ge 2, | 2 p. |
| sillä x^2 \ge 4 ja x-1 \ge 1, kun x \ge 2. | 1+1 p. |
| TAI | |
| Muodostettu funktio f(x)=x^3-x^2-4. | 1 p. |
| Ratkaistu nollakohdat ja laskettu testipisteet. | 1 p. |
| Päätelty funktion kulku. | 1 p. |
| Yhdistetty yllä olevat ja todettu, että epäyhtälö pätee. | 1 p. |
| Osatehtävän erillisohjeet | |
| Pelkkä Solve epäyhtälöstä, vastauksena x \ge 2. | 0 p. |
9. Integraalialgoritmi 12 p.
Tekstissä on esitetty pseudokoodilla kirjoitettu algoritmi.
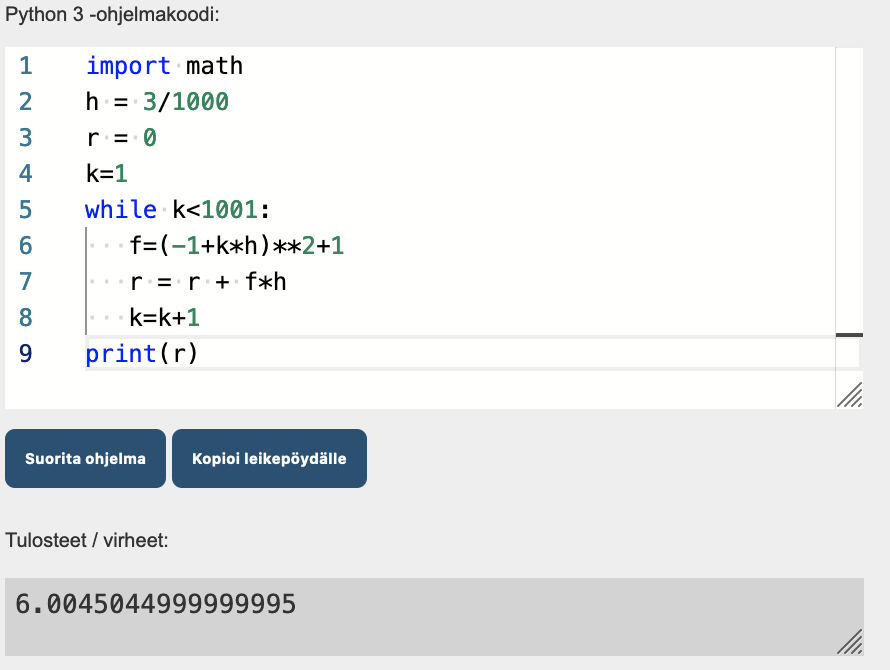
Minkä tuloksen algoritmi antaa, kun a=0, b=1 ja n=5? (2 p.)
Tee taulukkolaskenta- tai ohjelmointitoteutus algoritmille, kun a=-1, b=2 ja n=1000. Minkä tuloksen se tässä tapauksessa antaa? (4 p.)
Mitä integraalia algoritmi approksimoi? Selitä muuttujien a, b, n, h, r, k ja f roolit algoritmissa. (6 p.)
| h=\frac{b-a}{n}=\frac{1-0}{5}=\frac{1}{5} | |
| k=1: f=(0+1\cdot\frac{1}{5})^2+1=\frac{26}{25}, r=0+\frac{26}{25}\cdot\frac{1}{5}=\frac{26}{125}. | 1 p. |
| k=2: f=(0+2\cdot\frac{1}{5})^2+1=\frac{29}{25}, r=\frac{26}{125}+\frac{29}{25}\cdot\frac{1}{5}=\frac{11}{25}. k=3: f=(0+3\cdot\frac{1}{5})^2+1=\frac{34}{25}, r=\frac{11}{25}+\frac{34}{25}\cdot\frac{1}{5}=\frac{89}{125}. k=4: f=(0+4\cdot\frac{1}{5})^2+1=\frac{41}{25}, r=\frac{89}{125}+\frac{41}{25}\cdot\frac{1}{5}=\frac{26}{25}. k=5: f=(0+5\cdot\frac{1}{5})^2+1=2, r=\frac{26}{25}+2\cdot\frac{1}{5}=\frac{36}{25}\ (=1\mathrm{,}44). | 1 p. |
| Osatehtävän erillisohjeet | |
| Pelkkä oikea vastaus TAI pelkkä vastaus 1{,}04 (indeksivirhe). | 1 p. |
| Huolellinen selitys iteraatioista tai kuvakaappaus python-toteutuksesta tai taulukkolaskentatoteutuksesta riittää perusteluksi. | |
| Alkupiste: Laskettu f:n kaava, joka riippuu vain k:sta TAI tai laskettu funktion f arvot kaikilla 1\le k\le 5. | 1 p. |
| riippumaton f:n iteraatiokaava selitetty tai näkyy ymmärrettävässä muodossa. | 1 p. |
| riippumaton r:n iteraatiokaava selitetty tai näkyy ymmärrettävässä muodossa. | 1 p. |
| riippumaton Oikea vastaus 6\mathrm{,}005. Kaikki tarkkuudet kelpaavat. | 1 p. |
| riippumaton Näkyvissä python-koodi tai kuvakaappaus taulukkolaskentatoteutuksesta (vähintään viimeinen rivi, ks. esimerkki alla). | 1 p. |
| Osatehtävän erillisohjeet | |
| Koodin toteutus yleisillä lukujen a, b ja/tai n arvoilla ilman sijoituksia a=-1, b=2, n=1000. Pistevähennys ensimmäiseltä riviltä, johon virhe vaikuttaa. | –1 p. |
| Yleinen virhe: viimeinen iteraatio puuttuu. | max 3 p. |
| Esimerkkikuva Pythonilla tehdystä ratkaisusta | |
| Esimerkkikuva taulukkolaskennalla tehdystä ratkaisusta | |
| Määritetään f-sarakkeeseen lauseke =(–1+A3*$G$5)^2+1 ja r-sarakkeeseen lauseke =C2+B3*$G$5. Tällöin r-sarakkeessa lasketaan siis edellinen r-arvo ja uusi f-arvo yhteen. | |
| Viimeinen rivi näyttää tältä: | |
| Arvo on siis noin 6\mathrm{,}005. |
| Algoritmi approksimoi integraalin \int_{-1}^2(x^2+1)\,\mathrm{d}x arvoa ja | |
| riippumaton integroitava funktio on x^2+1, | 1 p. |
| riippumaton a on integroimisvälin alkupiste ja b integroimisvälin loppupiste, | 1 p. |
| riippumaton n kertoo, kuinka moneen osaväliin integroimisväli jaetaan (ja jokaisella osavälillä pinta-alaa approksimoidaan suorakulmiolla) ja h on osavälin pituus, | 1 p. |
| riippumaton r laskee osasumman arvoa, eli siihen summataan suorakulmioiden pinta-aloja, | 1 p. |
| riippumaton k on laskurin arvo, joka kertoo, kuinka monetta suorakulmiota käsitellään, | 1 p. |
| riippumaton f antaa sen funktion arvon, jota integroidaan. | 1 p. |
B2-osa
10. Positroniemissiotomografia 12 p.
Positroniemissiotomografia (PET) on lääketieteellinen kuvantamismenetelmä, jonka avulla voidaan mallintaa sisäelinten toimintaa. PET-kuvan avulla on mahdollista muodostaa aika-aktiivisuuskäyrä, joka on muotoa f(t)=g(t)+u e^{v-(t-w)^2}, missä u, v, w>0 ja
g(t)= \begin{cases} 0, &\text{kun } t<0,\\ a_1t+b_1, &\text{kun } 0\le t<w,\\ a_2t+b_2, &\text{kun } t\ge w. \end{cases}
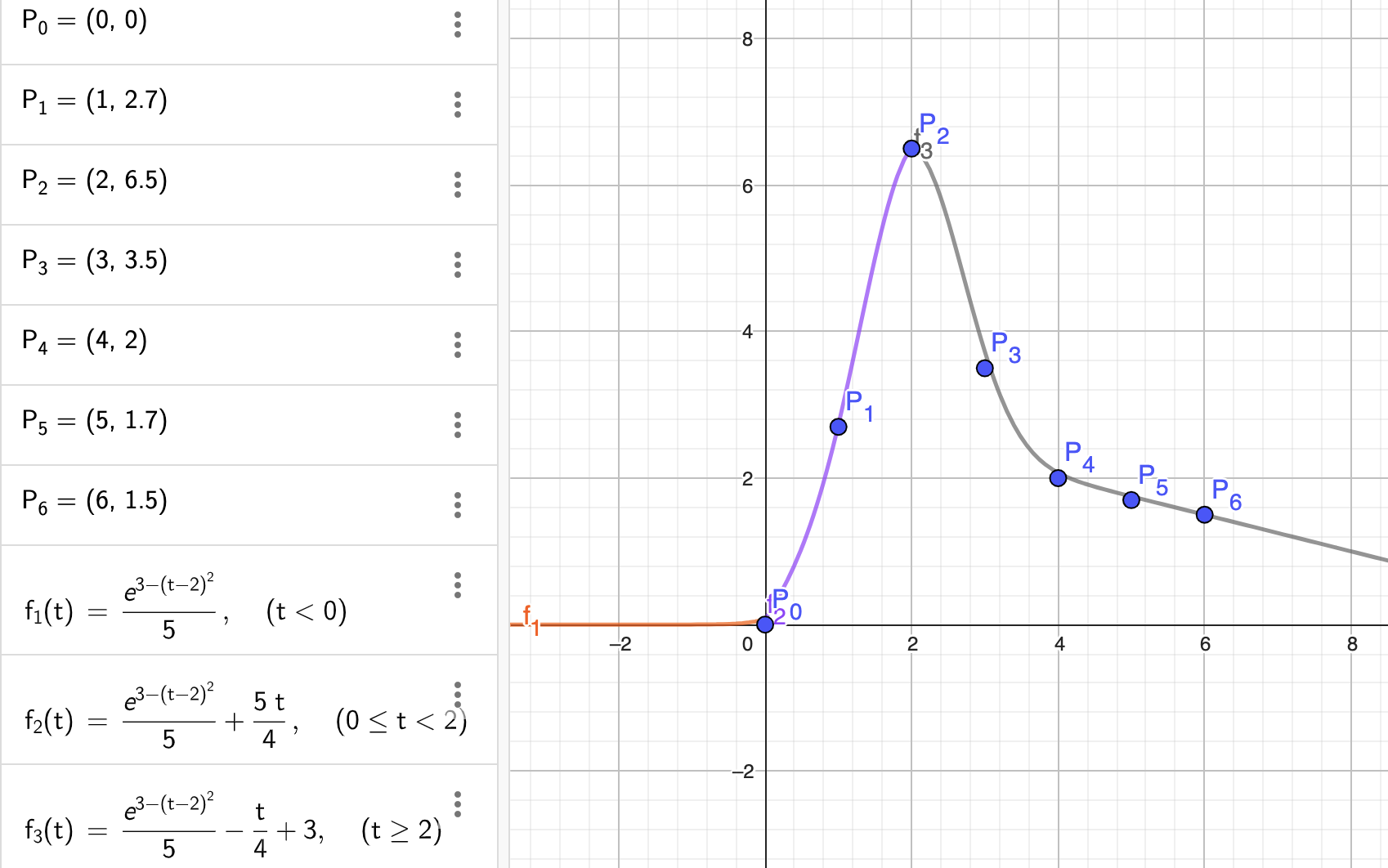
Taulukko sisältää erään PET-kuvan mittausarvot ajan funktiona. Mittaus voidaan mallintaa funktion f avulla, kun u=\frac15, v=3, w=2, a_1=\frac54, b_1=0, a_2=-\frac14 ja b_2=3. Piirrä funktion f kuvaaja ja mittausarvot koordinaatistoon. (4 p.)
Miten parametrit u, v ja w vaikuttavat funktion kuvaajaan? (4 p.)
Mitkä ehdot parametrien w, a_1, b_1, a_2 ja b_2 tulee toteuttaa, jotta funktio f on jatkuva? (4 p.)
| Käyrä osittain oikein (kaksi paloittain määritellyn funktion palaa). | 1 p. |
| Käyrä silmämääräisesti oikein. | 1 p. |
| riippumaton Pisteet silmämääräisesti oikein. | 1 p. |
| Oikea lauseke ja pisteiden oikeat koordinaatit ohjelmistoon syötettynä näkyvissä. | 1 p. |
| Osatehtävän erillisohjeet | |
| Pisteet asetettu käyrälle. | +0 p. |
| Pisteille polynomisovitus tai splini. | +0 p. |
| Muuttujana voi olla muukin kuin t. | –0 p. |
| Huomaa, että alustavassa arvostelussa ei välttämättä ole huomattu, että t<0 puuttuu. Pisteet: (1+0+1+0). | max 2 p. |
| Pisteet ja funktio piirretty eri koordinaatistoihin. | –0 p. |
| Alkupiste: Funktio g piirretty oikein. | 1 p. |
| Esimerkkikuva malliratkaisusta: | |
| Kun u kasvaa, niin funktion huippu nousee (tai suurin arvo kasvaa). | 1 p. |
| Kun v kasvaa, niin funktion huippu nousee (tai suurin arvo kasvaa). | 1 p. |
| Kaksi olennaisesti eri havaintoa parametrista w (piste per havainto). | 2 p. |
| Osatehtävän erillisohjeet | |
| Esimerkkejä havainnoista parametrin w suhteen: ”Parametri w vaikuttaa funktion jatkuvuuteen.”, ”Parametri w vaikuttaa huipun t-suuntaiseen sijaintiin.”, ”Parametri w määrää, milloin funktiossa vaihdetaan lauseketta.” | |
| ”Parametrit u ja v muuttavat huipun korkeutta.” Kahdelta ensimmäiseltä riviltä yhteensä | 1 p. |
| Selvästi väärä havainto kohdasta, josta annetaan pisteitä, osatehtävästä yhteensä: | –1 p. |
| Vähän turhaa tietoa (esimerkiksi mitä tapahtuu, kun u<0). | –0 p. |
| Kuvakaappaus, jossa negatiivinen parametri tai muuta vikaa. | –0 p. |
| Alkupiste: Testattu eri parametrien vaikutusta esimerkiksi liukusäätimellä. | 1 p. |
| riippumaton Todettu jatkuvaksi muualla kuin kohdissa t = 0 ja t = w. | 1 p. |
| Vertailtu lausekkeita muutoskohdissa t = 0 ja t = w. | (1 p.) |
| Johtopäätökset b_1 = 0 ja b_2 = w(a_1 - a_2). | 1 p. |
| Sovellettu jatkuvuuden määritelmää oikein kohdissa t = 0 ja t = w. | 1 p. |
| Osatehtävän erillisohjeet | |
| Yhtälö b_2 = w(a_1 - a_2) missä tahansa muodossa hyväksytään. | –0 p. |
| Tarkasteltu vain funktion g jatkuvuutta toteamatta eksplisiittisesti, että se riittää funktion f jatkuvuuteen. | –1 p. |
11. Nopanheiton opetus 12 p.
Eeri haluaa valita kahdesta nopasta paremman. Hän heittää niitä kerran ja valitsee nopan, joka antaa suuremman tuloksen. Jos kumpikin noppa antaa saman tuloksen, hän valitsee toisen nopista. Kummassakin tapauksessa Eeri heittää valitsemaansa noppaa uudestaan. Millä todennäköisyydellä nopan tulos toisella heitolla on pienempi kuin ensimmäisellä heitolla? (9 p.)
Laajasti levinneen uutisen mukaan maailman kymmenen rikkaimman ihmisen omaisuus kaksinkertaistui koronapandemian kahden ensimmäisen vuoden aikana. Väite perustui ilmeisesti siihen, että ajanjakson lopulla oli laskettu kymmenen rikkaimman ihmisen omaisuuden arvo ja verrattu sitä heidän omaisuuteensa kaksi vuotta aikaisemmin. Tähän sisältyy ajatusvirhe, joka tulee esiin myös Eerin nopanheitossa. Mikä se on? (3 p.)
| Paremman nopan määrittämisen yhteydessä (ks. osatehtävän erillisohjeet) todettu, että kahden nopan heitossa on 36 vaihtoehtoa TAI alkeistapauksen todennäköisyys on \frac1{36}. | 1 p. |
| Suurin silmäluku ja sitä vastaavien tapausten lukumäärät oikein: 6|11, 5|9, 4|7, 3|5, 2|3 ja 1|1. (1 p. jos kaksi oikein.) | 2 p. |
| riippumaton Perusteltu tapausten lukumäärät selityksellä tai kuviolla. | 2 p. |
| riippumaton Jos suurempi silmäluku on k‚ seuraavalla kierroksella todennäköisyys heittää pienemmän arvon todennäköisyys on \frac{k-1}{6}. (1 p., jos joku tapaus oikein TAI suotuisien tapausten lukumäärä on k-1.) | 2 p. |
| Vastaus laskettu omista luvuista oikealla logiikalla (ks. osatehtävän erillisohjeet) (oikea lasku \frac{11}{36} \cdot \frac{5}{6} + \frac{9}{36} \cdot \frac{4}{6} +\frac{7}{36} \cdot \frac{3}{6} +\frac{5}{36} \cdot \frac{2}{6} + \frac{3}{36} \cdot \frac{1}{6} = \frac{125}{216} \approx 0{,}579). | 2 p. |
| Osatehtävän erillisohjeet | |
| Vastauksen saa antaa desimaalilukuna; 0{,}6 tai tarkempi kelpaa. | |
| Rivin 1 pistettä ei saa siitä, jos 36 alkeistapausta tulevat laskettaessa uudelleen heiton todennäköisyyksiä (rivi 4), vrt. alla oleva max 3 -tapaus. | |
| Rivillä 5 ”oikealla logiikalla” tarkoittaa muotoa \sum_k p(k)p(A|k) tyyppistä laskua. Jos kaikki todennäköisyydet p(k) ovat samat, tältä riviltä 1 p. | |
| Rivillä 4 tulkittu ”pienempi tai yhtäsuuri” ja saatu todennäköisyys \frac{k}6. (1+2+2+1+2) | max 8 p. |
| Alussa on heitetty vain yhdellä nopalla ja laskettu \frac1{6} (\frac56 + \frac46 + \frac36 +\frac26 + \frac16) = \frac{5}{12}. (0+0+0+2+1) | max 3 p. |
| Alussa on heitetty vain yhdellä nopalla, 6\times 6 taulukosta laskettu 15 suotuisaa tapausta ja vastauksena \frac{15}{36} tai \frac{5}{12}. (0+0+0+1+1) | max 2 p. |
| Oikea ohjelmakoodi 8 p. ja selitys 1 p. |
| Uskottava huomio 10 rikkaimman omaisuuksien muutoksesta (esimerkiksi: ”Maailman kymmenen rikkaimman ihmisen yhteenlaskettu omaisuus voi kaksinkertaistua, vaikka osalla heistä omaisuuden arvo laskisi”). | (1 p.) |
| Samat ihmiset eivät välttämättä olleet 10 rikkaimman joukossa kaksi vuotta sitten. | 1 p. |
| riippumaton Mitä enemmän omaisuus kasvaa, sitä todennäköisemmin päätyy 10 rikkaamman ihmisen listalle TAI esitetty järkevä analogia 10 rikkaimman ihmisen listan ja Eerin nopan heiton välillä. | 1 p. |
| Osatehtävän erillisohjeet | |
| Esimerkki 3 pisteen vastauksesta: ”Kymmenen rikkaimman joukossa on todennäköisesti niitä, joiden varallisuus on kasvanut merkittävästi kahden vuoden aikana, eikä niitä, joiden omaisuus on kasvanut vähemmän.” | |
| Lisätieto: Tehtävässä käsitellään ”regression towards the mean” -ilmiötä. Tässä tapauksessa se ilmenee seuraavasti. Kummassakin tapauksessa tutkittava joukko valitaan sen perusteella, että tutkittavan muuttujan arvot ovat suuria. Jos muuttujan arvo on suuri sattumalta (kuten nopanheitossa), niin se todennäköisemmin pienenee. Rikkaiden ihmisten joukossa tämä tarkoittaa, että ne, joiden omaisuus on suuri, kun lista laaditaan, ovat todennäköisemmin niitä, joiden omaisuus vähenee tavallista enemmän kun mennään ajassa taaksepäin, eli toisin sanoen niitä, joiden omaisuuden arvo on kasvanut tavanomaista enemmän. |
12. Polynomikonstruktio 12 p.
Anna esimerkki polynomista P(x), joka toteuttaa seuraavat ehdot:
Yhtälöllä P(x)=1 on täsmälleen kaksi erisuurta ratkaisua, ja yhtälöllä P(x)=-1 on ainakin neljä erisuurta ratkaisua.
Täysien pisteiden arvoinen ratkaisu sisältää laskut, joista voidaan nähdä, että esimerkki toteuttaa vaaditut ehdot. Graafinen perustelu tai yhtälön ratkaisukäskyn käyttö eivät yksinään riitä täysiin pisteisiin.
| Vastauksena annettu yksi vähintään neljännen asteen polynomi TAI todettu, että lähdetään etsimään vähintään neljännen asteen polynomia TAI vähintään neljännen asteen polynomiperhe, jonka kertoimia pyritään määrittämään. | 1 p. |
| Vastauksessa tutkitaan yhtälöitä P(x)=1 ja P(x)=-1 algebrallisesti tai graafisesti TAI tutkitaan funktion kulkua (esimerkiksi perustelemattomalla kulkukaaviolla) TAI piirretty ohjelmistolla polynomin kuvaaja, ja kuvasta näkyy silmämääräisesti, että annettu polynomi toteuttaa vaaditut ehdot. | 1 p. |
| Osoitettu, että yhtälöllä P(x)=1 on täsmälleen kaksi ratkaisua JA että yhtälöllä P(x)=-1 ainakin neljä ratkaisua. Pistejaon täsmennys kummankin yhtälön osalta alla. | 5+5 p. |
| Pistejaon yleispiirteet: | |
| P(x)=-1: 2 p. ensimmäisestä ratkaisusta, 1 p./ratkaisu lopuista | 0+5 p. |
| P(x)=1 on ainakin kaksi erisuurta reaalista ratkaisua 2 p./ korkeintaan kaksi erisuurta reaalista ratkaisua 3 p. | 5+0 p. |
| Pistejako tarkemmin (pisteet annetaan sen rivin mukaan, mikä antaa parhaat pisteet): | |
| Likiarvoratkaisu ohjelmistosta vähintään neljännen asteen yhtälölle TAI graafinen ratkaisu (ratkaisut merkitty edes silmämääräisesti) TAI laskettu vain derivaatan nollakohdat ja muodostettu kulkukaavio. | 1 p. |
| Tarkka ratkaisu ohjelmistosta vähintään neljännen asteen yhtälölle. | 2 p. |
| Ratkaistu yli 3. asteen yhtälö välivaiheessa ohjelmistolla. | 3 p. |
Matemaattisesti perusteltu päättely, jossa hyväksytään:
| 5 p. |
| Tehtävän erillisohjeet | |
| Pisterivin 5+5 pisteet voi saada vain, jos yrittää saada kummatkin ehdot toteutumaan samalle polynomille (eli yleensä ei voi saada 0+5 tai 5+0). | |
| Konstruktiiviset ratkaisut arvioidaan saman ohjeen ja pistejakauman mukaan. | |
| Konstruktiossa asetettu funktiolle ja derivaatalle arvoja ilman auki kirjoitettua selitystä, miksi ne takaavat vaaditut ehdot (P(x)=1 ja P(x)=-1) (kummastakin ehdosta erikseen -1 piste). | max 11 p. |
| Vastauksena kaksi eri polynomia, yksi kummallekin ehdolle. | 0 p. |
| Ratkaistu lineaariset yhtälöryhmät ja toisen asteen yhtälöt ohjelmistolla. | –0 p. |
| Ratkaistu ohjelmistolla yhtälöitä tarkistusmielessä. | –0 p. |
| Polynomi saatu sovittamalla pisteisiin. | +0 p. |
| Alkupiste: Hahmoteltu tilanne graafisesti kuvaajalla sekä suorilla y=1 ja y=-1 (polynomin lauseke puuttuu tai on vääränlainen). Jos vastaus ei käsittele vähintään neljännen asteen polynomia, ei tehtävästä anneta muita pisteitä. | 1 p. |
13. Integraalin ja raja-arvon järjestyksen vaihto 12 p.
Olkoon \displaystyle f(x,s)=\frac{1-s}{(1+x^2-2sx)^2}, kun 0<s<1 ja 0\le x\le 1. Tarkastellaan vasemmanpuoleista raja-arvoa \displaystyle\lim_{s\to 1}, jota joskus merkitään \displaystyle\lim_{s\to 1^-}.
Määritä \displaystyle g(x)=\lim_{s\to 1} f(x,s) kaikilla 0\le x<1, ja laske \displaystyle \int_0^1 g(x)\, dx. (3 p.)
Määritä sellainen x_0<1, että f(x_0, s) = f(1, s), ja laske \displaystyle \int_{x_0}^1 f(x_0,s)\, dx. (3 p.)
Osoita, että f(x, s) \ge f(x_0, s), kun x\in [x_0, 1] ja x_0 on määritetty osatehtävässä 13.2. (3 p.)
Osoita, että \displaystyle \int_0^1 \lim_{s\to 1} f(x,s)\, dx \ne \lim_{s\to 1} \int_0^1 f(x,s)\, dx. (3 p.)
| Yritetään laskea raja-arvoa oikeassa kohdassa ja oikean muuttujan suhteen. | 1 p. |
| g(x)=\lim_{s\rightarrow 1}f(x,s)=\lim_{s\rightarrow 1}\frac{1-s}{(1+x^2-2sx)^2}=0 (kun 0\leq x<1). | 1 p. |
| Siispä \int_0^1g(x)\,\mathrm{d}x=0. | 1 p. |
| Tämän ratkaisun erillisohjeet | |
| Lisätieto: Kun x=1, niin \lim_{s\rightarrow 1}f(x,s)=\lim_{s\rightarrow 1}\frac{1-s}{(1+1^2-2s\cdot1)^2}=\infty. |
| Ratkaistaan yhtälö \frac{1-s}{(1+x^2-2sx)^2}=\frac{1-s}{(1+1^2-2s\cdot1)^2}. Koska nimittäjissä 2-2s>0 ja h(x,s)=1+x^2-2sx>1+x^2-2x=(1-x)^2\geq 0, yhtälö voidaan sieventää muotoon x^2-2sx=1-2s, joka voidaan kirjoittaa tulona (1-x)(x+1-2s)=0. | 1 p. |
| Nyt x=1 tai x=2s-1. Kysytty arvo on siis x_0=2s-1, ja funktion arvo tässä pisteessä on f(2s-1,s)=f(1,s)=\frac{1-s}{(2-2s)^2}. | 1 p. |
| Integraali on \int_{x_0}^1\frac{1-s}{(2-2s)^2}\,\mathrm{d}x=\frac{1-s}{(2-2s)^2}(1-x_0)=\frac{1-s}{(2-2s)^2}(1-(2s-1)) =\frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| Kiinteällä s on h(x,s)=x^2+1-2sx ylöspäin aukeava paraabeli ja h(x_0,s)=h(2s-1,s)=(2s-1)^2+1-2s(2s-1)= -2s+2 =h(1,s), joten h(x,s)\leq h(x_0,s) kaikilla x\in [x_0,1]. | 1 p. |
| Koska lisäksi h(x,s)=x^2-2 s x +1 >(1-x)^2\geq 0, on h(x,s)^2\leq h(x_0,s)^2 kaikilla x\in [x_0,1]. | 1 p. |
| Koska f(x)=\frac{1-s}{h(x,s)}, niin f(x,s)\geq f(x_0,s) kaikilla x\in [x_0,1]. | 1 p. |
| Arvioidaan \lim_{s\rightarrow 1}\int_0^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1}\int_{x_0}^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1} \frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| Nyt raja-arvot ovat erisuuret, sillä \int_0^1\lim_{s\rightarrow 1}f(x,s)\,\mathrm{d}x=\int_0^1g(x)\,\mathrm{d}x=0. | 2 p. |
| TAI Ohjelmistolla tehdyt ratkaisut |
| Määritellään tarkasteltava funktio oikein f(x,s):=\frac{1-s}{(1+x^2-2\cdot x \cdot s)^2 } ja g(x)=\lim_{s\rightarrow 1-}f(x,s) josta g(x)=0 (kun 0\leq x<1) | 2 p. |
| Siispä \int_0^1g(x)\,\mathrm{d}x =0. Tähän pisteeseen funktion f täytyy olla oikein määritelty ja g saatu vasemmanpuoleisena raja-arvona. | 1 p. |
| Tämän ratkaisun erillisohjeet | |
| Jos raja-arvo ei ole vasemmanpuoleinen TAI funktion g lauseketta ei näy (edes muodossa \lim f = 0, g=\lim f). | 1+1 p. |
| Jos muuttujien väliin ei ole laitettu kertomerkkiä, saattaa ohjelmisto tulkita tulon xs muuttujana xs. Tässä osatehtävässä virhe ei näy selvästi. Siksi tästä osatehtävästä ei vähennystä, mutta tällä määrittelyllä jatkosta ei voi saada pisteistä. | –0 p. |
| \mathrm{solve}(f(x_0,s)=f(1,s),x_0), josta x_0=\pm\sqrt{s^2+2 s-3} +s, \ x_0=2s-1, \ x_0=1. | 1 p. |
| Näistä vain x_0=2s-1 kelpaa, koska x_0<1 ja juurrettava on tarkasteluvälillä negatiivinen, sillä \mathrm{solve}(s^2+2s-3<0,s), josta -3<s<1. | 1 p. |
| \int_{2s-1}^1 f(2s- 1, s ) \, dx = \frac{1}{2}. | 1 p. |
| Tämän ratkaisun erillisohjeet | |
| Väärä määrittely johtaa ”ratkaisuihin” x_0= \pm\sqrt{4sx-3}, \ x_0=\pm 1. | 1 p. |
| Yhtäpitävästi voidaan tutkia funktiota g(x,s):=f(x,s)-f(2s-1,s). Etsitään derivaatan k(x,s):=\frac{d}{dx} g(x,s)=\frac{4(s-1)(s-x)}{(2\cdot s \cdot x-x^2-1)^3}, nollakohdat \mathrm{solve}(k(x,s)=0,x), josta x=s tai s=1, | 1 p. |
| s kuuluu tarkasteluvälille, sillä \mathrm{solve}(2s-1\leq s \leq 1,x), josta s\leq 1. | 1 p. |
| Koska g(2 s-1,s)=0 ja g(s,s)=\frac{s+3}{4\cdot(s+1)^2}, on erotuksen pienin arvo 0 ja epäyhtälö pätee | 1 p. |
| Tämän ratkaisun erillisohjeet | |
| Väärän määrittelyn antamat ratkaisut x_0 eivät ole mielekkäitä tässä osatehtävässä. | 0 p. |
| Arvioidaan \lim_{s\rightarrow 1}\int_0^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1}\int_{x_0}^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1} \frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| Nyt raja-arvot ovat erisuuret, sillä \int_0^1\lim_{s\rightarrow 1}f(x,s)\,\mathrm{d}x=\int_0^1g(x)\,\mathrm{d}x=0. | 2 p. |