Beskrivningar av goda svar: SV – Matematik, lång lärokurs
22.3.2023
Slutgiltiga beskrivningar av goda svar 16.5.2023
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal i den högra kolumnen för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i parentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Terminologi
- ''Svar räcker'' betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- ''Startpoäng'' betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- ''maxN'' betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- ''Svaret endast som närmevärde'' betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (t.ex. noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (t.ex. e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (t.ex. e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (t.ex. x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (t.ex. parenteser som fattas men korrekt beräknat; =-tecknet använt ''i kedja'', m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Instruktioner för anvisningar med tre kolumner:
- Examinanden får poäng från idékolumnen om hen har börjat utföra den nämnda operationen, även om genomförandet skulle vara bristfälligt.
- En beräkning eller en formel i genomförandekolumnen visar hur idén ser ut då den är korrekt utförd.
- Stoppvillkor: från varje rad ska man få minst hälften av radens poäng, nedåt avrundade, för att man ska kunna fortsätta.
- Om stoppvillkoret inte uppfylls, dvs. om det ännu finns poäng som kan delas ut på följande rader, så kan examinanden ännu få alla poäng från de följande raderna, där det inte explicit finns något hinder för att hen inte ska kunna få poängen.
Del A
1. Flervalsuppgift 12 p.
Välj korrekt alternativ. Svaren behöver inte motiveras. Rätt svar 2 p., fel svar 0 p., inget svar 0 p.
1.1 Måttenheter 2 p.
- 10^{6} (2 p.)
1.2 Cylinder 2 p.
- prisma (2 p.)
1.3 Cosinussatsen 2 p.
- Pythagoras sats (2 p.)
1.4 Riktningskoefficient 2 p.
- derivatans värde för funktionen f(x)=ax+b som bildas av linjens ekvation (2 p.)
1.5 Skalär produkt 2 p.
- Felaktigt svar som ger poäng: ett heltal (1 p.)
- ett reellt tal (2 p.)
1.6 Skärningspunkter 2 p.
- högst fyra skärningspunkter (2 p.)
2. Kombinering 12 p.
Nedan är 12 ekvationer givna. Nio av dem motsvarar någon av de givna graferna i figur . Förena var och en av ekvationerna med dess motsvarande graf eller välj att ingen sådan finns.
Välj korrekt alternativ. Svaren behöver inte motiveras. Rätt svar 1 p., fel svar 0 p., inget svar 0 p.
2.1 1 p.
- Graf 9 (1 p.)
2.2 1 p.
- Graf 2 (1 p.)
2.3 1 p.
- Ingen graf (1 p.)
2.4 1 p.
- Graf 12 (1 p.)
2.5 1 p.
- Graf 4 (1 p.)
2.6 1 p.
- Graf 5 (1 p.)
2.7 1 p.
- Graf 7 (1 p.)
2.8 1 p.
- Graf 1 (1 p.)
2.9 1 p.
- Graf 10 (1 p.)
2.10 1 p.
- Ingen graf (1 p.)
2.11 1 p.
- Graf 3 (1 p.)
2.12 1 p.
- Ingen graf (1 p.)
3. Järnvägsspår 12 p.
Ett tio meter långt museijärnvägsspår har på grund av värmeutvidgning vridits till en kurva, men dess ändar har hållits på plats (se den överdrivna figuren av situationen). Spårets avvikelse från det ursprungliga läget vinkelrätt uppmätt har formen
f(x)=\frac{x^3-15x^2+50x}{1000},
då x är avståndet från spårets startända. I vilka punkter är spårets avvikelse från det ursprungliga läget så stor som möjligt? Bestäm även den största avvikelsen. Enheten för variabeln x och för avvikelsen är meter.
| Funktionens derivata f'(x)=\frac{1}{1000}(3x^2-30x+50) har beräknats. | 2 p. |
| Om derivatan inte är ett andragradspolynom så är endast oberoende -radens poäng möjliga att dela ut i fortsättningen. | |
| Derivatans nollställen (närmevärden med tillräcklig noggrannhet duger) x=\frac{30\pm 10\sqrt{3}}{2\cdot 3}=5\pm \frac{5}{\sqrt{3}} (2{,}1132\ldots och 7{,}8867\ldots). | 2 p. |
| Beräkning av funktionens värden i de nollställen till derivatan som tillhör intervallet ]0,10[. | 1+1 p. |
| oberoende Examinanden har konstaterat att de största avvikelserna hittas i derivatans nollställen. Detta är motiverat på något sätt (exempelvis med en figur eller med ett teckenschema utan begränsning för intervallet). | 2 p. |
| Examinanden har jämfört avvikelser i derivatans nollställen, som ligger i intervallet ]0,10[. | (1 p.) |
| Svaren är angivna som närmevärden 2\mathrm{,}11 (m) och 7\mathrm{,}89 (m) och avvikelsen 0\mathrm{,}048 (m), punkterna för avvikelserna måste vara i intervallet ]0,10[. | 3 p. |
| Specifika anvisningar för denna lösning | |
| I lösningen kan man också granska endast täljarens derivata. | |
| Den negativa avvikelsen -0{,}048 har angetts i svaret. | max 12 p. |
| Fel i deriveringen och derivatan är ett andragradspolynom (1+2+2+2+2+2). | max 11 p. |
| Ett fel i beräkningen av derivatans nollställen, där följden är att man fått endast ett nollställe till derivatan i det intervall som granskas (2+1+1+2+0+2). | max 8 p. |
| Examinanden har hänvisat till symmetri med avseende på punkten x=5 och beräknat endast den ena avvikelsen (2+2+1+2+1+3). | max 11 p. |
| Examinanden har tolkat den största avvikelsen som det största värdet och funktionens värde f(7{,}88\ldots) har inte beräknats (2+2+1+2+0+2). | max 9 p. |
| ELLER Prövnings- eller programmeringslösning. | |
| Examinanden har med hjälp av tre punkter vid båda topparna visat att man i den mittersta får det största/minsta värdet, avståndet mellan punkterna är högst en tiondel (exempelvis 2\mathrm{,}0; 2\mathrm{,}1 och 2\mathrm{,}2 och motsvarande för den andra). | 1+1 p. |
| oberoende Examinanden har tagit fram x-koordinaterna på rätt sätt när det kommer till gällande siffror (exempelvis för värdena i punkterna 2\mathrm{,}0; 2\mathrm{,}1 och 2\mathrm{,}2 konstaterat att värdet av x är ungefär 2). | 1+1 p. |
| Jämförelse av avvikelserna i topparna. | 1 p. |
| Den givna avvikelsen är 0\mathrm{,}048 m och vid beräkningen av avvikelsen finns minst en gällande siffra mer än i svaret. | 1 p. |
| Examinanden har gett punkterna för avvikelserna med närmevärdena 2\mathrm{,}11 m och 7\mathrm{,}89 m med korrekta motiveringar. | 2 p. |
| oberoende f(0)=0 och f(10)=0 ELLER ändpunkterna rör sig inte ELLER begränsning till det slutna intervallet [0,10]. | 1 p. |
| Motivering för varför det inte finns andra lokala extremställen (exempelvis att ett tredjegradspolynom har högst två lokala extremställen). | 3 p. |
| Specifika anvisningar för denna lösning | |
| Examinanden har använt sig av testpunkterna 2\mathrm{,}10; 2\mathrm{,}11 och 2\mathrm{,}12, och på ett felaktigt sätt konstaterat att toppen är i punkten 2\mathrm{,}11 och symmetriskt i en annan punkt och angett som avvikelse 0\mathrm{,}048 eller 0\mathrm{,}05 (2+0+1+1+0+1+3). | max 8 p. |
| En prövningslösning där examinanden inte har använt tre förnuftiga testpunkter för att hitta toppen (Exempelvis så har avvikelsen endast beräknats för värdena 2\mathrm{,}11 och 2\mathrm{,}12) (0+0+0+0+0+1+0). | max 1 p. |
| Examinanden har hänvisat till grafens symmetri och felaktigt påstått att avvikelserna är 2\mathrm{,}5 och 7\mathrm{,}5 (0+0+0+0+0+1+0). | max 1 p. |
| Startpoäng: funktionens värden har beräknats i två punkter i intervallet [0, 10]. | 1 p. |
4. Avståndet från en linje till två punkter 12 p.
Bestäm alla räta linjer som har avståndet 2 till punkten A=(-2,0) och avståndet 3 till punkten B=(3,0).
| Idékolumn | Genomförandekolumn | Poäng |
| oberoende Linjen x=0 ELLER y-axeln uppfyller tydligt villkoren i uppgiftsbeskrivningen. | 0+1 p. | ||
| Den linje som söks tangerar cirklar och är vinkelrät mot cirklarnas radier ELLER motsvarande villkor formulerade på ett annat sätt (exempelvis utan cirklar). | 2+0 p. | ||
| Förnuftiga valda rätvinkliga trianglar / likformighet tillämpat på trianglar för att lösa ut skärningspunkten med x-axeln. | (Rätvinklig triangel, hörnen B=(3, 0), linjen och den större cirkelns tangeringspunkt P och linjens skärningspunkt med x-axeln Q.) Vi får en proportionalitetsekvation i en triangel av rätt typ: \frac{3}{5+z}=\frac{2}{z}, där z är avståndet mellan punkterna (-2,0) och Q. Därmed är z=10. Linjen skär alltså x-axeln i punkten (-12, 0). | [1+1] +[1+1] p. | |
| Riktningskoefficienten k bestäms via någon förnuftigt vald triangel. | De uppgifter som behövs för att beräkna riktningskoefficienten (exempelvis kateterna) och linjens riktningskoefficient k=\frac{h}{15}=\frac{1}{\sqrt{24}}. | 0+3 p. | |
| Linjens ekvation är y=\frac{1}{\sqrt{24}}(x+12), och ekvationen för den linje som går under x-axeln är på motsvarande sätt y=-\frac{1}{\sqrt{24}}(x+12). | 0+[1+1] p. | ||
| oberoende Linjen x=0 ELLER y-axeln uppfyller tydligt villkoren i uppgiftsbeskrivningen. | 0+1 p. | ||
| Då man rör sig 5 enheter x-axeln mot vänster, så minskar avståndet till linjen från tre till två. | Då man rör sig ytterligare två gånger fem enheter minskar avståndet till noll, varvid linjen skär x-axeln i punkten x=-12. | 1+[1+1] p. | |
| Idé om det att de sökta linjerna tangerar cirklarna och att linjerna är vinkelräta mot cirklarnas radier. | Nu bestäms de övriga linjerna. De är två till antalet och de är symmetriska med avseende på x-axeln. Den ena linjen tangerar cirklarna (x-3)^2+y^2=3^2 och (x+2)^2+y^2=2^2 ovanifrån och den andra underifrån. | [1+1]+0 p. | |
| Vi ritar någon förnuftig rätvinklig triangel med tanke på situationen. | Riktningskoefficienten bestäms exempelvis av en rätvinklig triangel, vars hypotenusa har längden 10 och motstående katet längden 2. Därmed är den närmare katetens längd \sqrt{96}, och riktningskoefficienten är \frac{2}{\sqrt{96}} = \frac{1}{\sqrt{24}}. | 1+3 p. | |
| Linjens ekvation är y=\frac{1}{\sqrt{24}}(x+12), och ekvationen för den linje som går under x-axeln är på motsvarande sätt y=-\frac{1}{\sqrt{24}}(x+12). | 0+[1+1] p. | ||
| oberoende Linjen x=0 ELLER y-axeln uppfyller tydligt villkoren i uppgiftsbeskrivningen. | 0+1 p. | ||
| Formeln för avståndet från en punkt till en linje används förnuftigt (avståndet och punkten har satts in på något sätt). | Två ekvationer: \dfrac{|-2a+c|}{\sqrt{a^2+b^2}}=2, \dfrac{|3a+c|}{\sqrt{a^2+b^2}}=3 ELLER \dfrac{|-2k+b|}{\sqrt{k^2+1}}=2, \dfrac{|3k+b|}{\sqrt{k^2+1}}=3 | 1+1 p. | |
| Examinanden strävar efter en ekvation med två variabler (vettig start) ELLER ursprungligen endast två variabler i ekvationsparet. | Exempelvis \dfrac{|-2a+c|}{2}=\dfrac{|3a+c|}{3} ELLER \dfrac{|-2k+b|}{2}=\dfrac{|3k+b|}{3} ELLER b^2=4+4kb=9-6kb | 1+2 p. | |
| Examinanden strävar efter att lösa ut en variabel med hjälp av den andra. | c=0 eller c=12a ELLER b=12k eller b=0 ELLER b=\frac{1}{2k} | 1+1 p. | |
| Insättning i den ursprungliga ekvationen och lösning av någon av variablerna. | b=\pm 2\sqrt{6}\,a ELLER b=\pm\sqrt{6},\ k=\pm\dfrac{1}{2\sqrt{6}} | 1+1 p. | |
| Linjernas ekvationer är y=\frac{1}{2\sqrt{6}}x+\sqrt{6} och y=-\frac{1}{2\sqrt{6}}x-\sqrt{6}. | 0+[1+1] p. | ||
| Specifika anvisningar för uppgiften | |||
| Närmevärden eller riktningskoefficienten med hjälp av trigonometriska funktioner: sista radens poäng blir outdelade (k=0{,}20412\dots, b=2{,}44948\dots). | |||
Del B1
5. En magisk kvadrat 12 p.
Koppargravyren Melancholia I (se figur ) tillhör tysken Albrecht Dürers mest kända konstverk. Konstverket innehåller en magisk 4\times 4-kvadrat, där summan av talen i varje vågrät och lodrät rad är 34. I rutfältet nedan framställs fyra rutor i den magiska kvadraten med hjälp av de obekanta talen x och y. Då man ställer upp talen x och y efter varandra får man som resultat det årtal då konstverket är producerat. Lös ut talen x och y och skriv ut det årtal som det är fråga om.
\begin{array}{|c|c|c|c|} \hline 16 & 3 & 2 & 13\\ \hline 5 & 10 & 11 & 8\\ \hline 9 & \frac{y-2}2 & \frac{x-1}2 & 12\\ \hline 4 & x & y & 1\\ \hline \end{array}
| Från den sista vågräta raden och den tredje lodräta raden får vi ekvationerna 4+x+y+1=34 och 2+11+\frac{x-1}{2}+y=34. | 3+3 p. |
| Genom att lösa ekvationsparet (ex. solve-kommandot) löses talen x=15 och y=14 ut (korrekt start / den ena variabeln har lösts ut med hjälp av den andra / båda är beräknade). | 1+1+1 p. |
| Det efterfrågade årtalet är alltså 1514 ELLER 1415. | 1 p. |
| Vi granskar vidare att de här värdena uppfyller de övriga två ekvationerna: den tredje vågräta raden 9+\frac{14-2}{2}+\frac{15-1}{2}+12=34 och den andra lodräta raden 3+10+\frac{14-2}{2}+15=34. | 1+1 p. |
| Specifika anvisningar för denna lösning | |
| På den första poängraden ger den första ekvationen 3 p. och en annan som är linjärt oberoende av den första 3 p. | |
| Ekvationssystemet korrekt, svaret ges utan omnämnande av ekvationssystemets lösning: allmänt avdrag -1 p. | |
| ELLER | |
| Prövning (fyra gånger), att med valen x=15 och y=14 så blir rad- eller kolumnsumman 34. | 2*4 p. |
| Minst två linjärt oberoende testningar och svaret 1514 ELLER 1415. | 1 p. |
| Motiverad entydighet. | 3 p. |
| Specifika anvisningar för denna lösning | |
| Prövning med några andra tal, av det första uppfyllda villkoret: | 2 p. |
| Examinanden har använt diagonalernas summor som villkor, 2 p. för vardera ekvationen och 1 p. för svaret. (Om det dessutom ingår kontroll av villkoren för vågräta och lodräta rader, poänggivning enligt den senare anvisningen utan tilläggspoäng för diagonalvillkoret.) | 5 p. |
6. Noskonen på en raket 12 p.
Vi får fram spetsen på en viss raket, den så kallade noskonen, genom att låta en nedåtvänd parabel rotera kring sin symmetriaxel. Spetsens höjd är 4,5 meter, och dess diameter vid bottnen är 3,3 meter. Bestäm spetsens volym.
| Lösningens start: Konstruktion av parabeln | |
| Först görs en modell av tvärsnittsparabeln. Vi placerar den i koordinatsystemet så att den har nollställena i punkterna x=\pm\frac{3\mathrm{,}3}{2}=\pm 1\mathrm{,}65\ (=\frac{33}{20}). | (2 p.) |
| Parabelns ekvation är alltså y=a(x-1\mathrm{,}65)(x+1\mathrm{,}65). | 2 p. |
| Tvärsnittets höjd är parabelns y-koordinat i den punkt där parabeln skär y-axeln. Det här får man alltså av ekvationen 4\mathrm{,}5=-a\cdot 1\mathrm{,}65^2, dvs. a=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}\ (=-\frac{200}{121}). | 2 p. |
| Som parabel har man alltså fått y=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}\left(x^2-1\mathrm{,}65^2\right)\ (=-\frac{200}{121}x^2+\frac{9}{2}), | 1 p. |
| ELLER (lösningens start på annat sätt) | |
| Först görs en modell av tvärsnittsparabeln. Vi placerar den i koordinatsystemet så att den öppnar sig neråt och att dess topp ligger i punkten (0;\ 4{,}5). | (2 p.) |
| Parabelns ekvation är alltså y=4{,}5+a(x-0)^2 ELLER y=4{,}5+ax^2 ELLER en ekvivalent form. | 2 p. |
| Insättning av den ena av parabelns nollställen x=\pm1{,}65 i ekvationen, vilket ger -4{,}5=a(1{,}65)^2 dvs. a = -4{,}5/(1{,}65^2). | 2 p. |
| Som parabel har man alltså fått y=-\frac{4\mathrm{,}5}{1\mathrm{,}65^2}x^2+4{,}5, | 1 p. |
| Lösningens slut: beräkning av integralen | |
| av vilket x=\pm \sqrt{-\frac{1\mathrm{,}65^2}{4\mathrm{,}5}y+1\mathrm{,65}^2}. | 1 p. |
| Beräkning av volymen för en rotationskropp med integralen \pi \int_0^{4\mathrm{,}5}\left(-\frac{1\mathrm{,}65^2}{4\mathrm{,}5}y+1\mathrm{,65^2}\right)\mathrm{d}y | 2 p. |
| \approx 19\mathrm{,}2442\approx 19 (kubikmeter). | 2 p. |
| Specifika anvisningar för denna lösning | |
| Examinanden märker att a=-\frac{200}{121}=-1{,}652... är nära talet -1{,}65. Om a=\frac{3{,}3}{2}, värdet på konstanten a uppkommer ur tomma intet eller om det annars är klart felaktigt, så (2+2+0+0+1+2+2). Det här gäller inte fel som uppstår på grund av slarv där tanken är korrekt. | max 9 p. |
| I integreringen på den nästsista raden så kan flera saker gå fel. Här är exempel på poäng för de två sista raderna: | |
| I integralen på den näst sista raden saknas \pi, men den är i övrigt korrekt. | max 3 p. |
| Det uttryck som integreras är ett x i stället för x^2. | max 1 p. |
| Helt fel volym (parabeln har exempelvis satts att rotera kring fel axel). | 0 p. |
| ELLER | |
| Ett ekvationssystem med tre ekvationer som ger parabelns koefficienter (1 p./korrekt ekvation). | 3 p. |
| Man har fått fram koefficienterna för en egen parabel (1 korrekt 1 p, 3 korrekta 2 p.). | 2 p. |
| Motivering för lösningen av ekvationssystemet (exempelvis solve- eller GG-kommando). | 1 p. |
| Korrekt egen parabel (exempel i formen y=f(x)), | 1 p. |
| av vilket man löst ut x. | 1 p. |
| Rotationskroppens volym skriven som en integral. | 2 p. |
| Svaret \approx 19\mathrm{,}2442\approx 19 (kubikmeter). | 2 p. |
| ELLER | |
| (Noskonen är en rotationsparaboloid, vars) volym är \frac{1}{2}\pi r^2h, | 2 p. |
| oberoende där radien är r=\frac{3\mathrm{,}3}{2}=1\mathrm{,}65 (meter) och höjden h=4\mathrm{,}5 (meter). | 2 p. |
| Volymen är alltså \frac{1}{2}\pi\cdot 1\mathrm{,}65^2\cdot 4\mathrm{,}5 (radien 3 p., höjden 3 p.) | 6 p. |
| \approx 19\mathrm{,}2442\approx 19 (kubikmeter). | 2 p. |
| Specifika anvisningar för denna lösning | |
| Examinanden har beräknat volymen med volymformeln för en kon (0+2+0+0). | max 2 p. |
| Beräknat med diagonalens längd (2+1+3+2). | max 8 p. |
| Specifika anvisningar för uppgiften | |
| Parabeln kan placeras i koordinatsystemet på olika sätt, också vågrätt. |
7. Vektoraddition 12 p.
Vi granskar vektorerna \overline{u}=\overline{i}+2 \,\overline{j} och \overline{v} = \sin(2t)\overline{i} + \cos(4t) \overline{j}, där t \ge 0.
Bestäm vektorn \overline{u}+\overline{v}, då t=0, t=\frac\pi 4 och t=\frac{3\pi}4. (4 p.)
Vilken planfigur bildas av ändpunkten till vektorn \overline{u}+\overline{v} då t får värdena i intervallet [0, \pi]? Ange svaret som en ekvation i formen y=f(x). I lösningen kan man till exempel använda sig av formeln \cos (2x)=1-2\sin^2 x. (8 p.)
| Examinanden har korrekt satt in något av de tre värdena på t i summans uttryck. | 1 p. |
| t=0: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin(2\cdot 0)\overline{i}+\cos (4\cdot 0)\overline{j}=\overline{i}+3\overline{j} | 1 p. |
| t=\frac{\pi}{4}: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin\left(2\cdot \frac{\pi}{4}\right)\overline{i}+\cos \left(4\cdot \frac{\pi}{4}\right)\overline{j}=2\overline{i}+\overline{j} | 1 p. |
| t=\frac{3\pi}{4}: \overline{u}+\overline{v}=\overline{i}+2\overline{j}+\sin\left(2\cdot \frac{3\pi}{4}\right)\overline{i}+\cos \left(4\cdot \frac{3\pi}{4}\right)\overline{j}=\overline{j} | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Svaren i formen 1i+3j, 2i+1j eller 0i+1j. | –0 p. |
| Svaren i en annan form, exempelvis med programvara svaret [0\ 1]. | –0 p. |
| Närmevärden i mellansteg (exempelvis \pi\approx 3{,}14), totalt | –1 p. |
| Endast svar (exempelvis som skärmdumpar av resultat framtagna med programvara). | max 2 p. |
| Räknaren inställd på grader. | 1+1+0+0 p. |
| Startpoäng: Något av sin- eller cos-värdena förenklade utan vektorer. | 1 p. |
| Uttrycken \sin(2t)+1 och \cos (4t)+2 förekommer (exempelvis som koefficienter redan i 7.1). | 1 p. |
| Beteckning av x=\sin(2t)+1 och y=\cos (4t)+2. | 1 p. |
| Vi får kurvan y=\cos (4t)+2=1-2\sin^2(2t)+2=3-2\sin^2(2t)=3-2(x-1)^2 (=1+4x-2x^2) (användning av formeln och x-formen: 2+2), | 4 p. |
| där x får värden i intervallet [0,2] och motivering (extrempunkterna exempelvis med valen t=\frac{3\pi}{4} och t=\frac{\pi}{4}.) | 2 p. |
| ELLER | |
| Uttrycken \sin(2t)+1 och \cos (4t)+2 förekommer (exempelvis som koefficienter redan i 7.1). | 1 p. |
| Uttrycken \sin(2t)+1 och \cos(4t)+2 insatta i ett program. | 1 p. |
| En parabelbåge uppritad, | 1 p. |
| då t varierar i korrekt intervall. | 1 p. |
| Parabelns koefficienter har tagits fram exempelvis med hjälp av tre punkter. | 1 p. |
| Tilläggsmotiveringar för parabeln. | 3 p. |
| ELLER | |
| t=\frac{1}{2}\sin^{-1}(x-1), av vilket y=\cos(2\sin^{-1}(x-1))+2 i intervallet [0, 2] och ett omnämnande av en parabel: (1)+2+2+1 | max 6 p. |
8. Jämförelse av polynom 12 p.
Visa med induktion att k^3\ge k^2+4 för varje heltal k\ge 2. (6 p.)
Visa att olikheten i deluppgift 8.1 inte gäller för något heltal k<0. (2 p.)
Visa att olikheten x^3\ge x^2+4 gäller för alla reella tal x\ge 2. (4 p.)
| oberoende Induktionens startsteg: Då k=2, är den givna olikheten 2^3\geq 2^2+4, dvs. 8\geq 8, som är sann. | 1 p. |
| Induktionsantagande: Vi antar att det för något värde på talet k\geq 2 gäller att k^3\geq k^2+4. | 1 p. |
| Induktionspåstående: Vi påstår att (k+1)^3\geq (k+1)^2+4. | 1 p. |
| (k+1)^3=k^3+3k^2+3k+1 | (1) p. |
| I induktionspåståendets bevis har induktionsantagandet använts (vänstra ledet k^3+3k^2+3k+1\geq k^2+4+3k^2+3k+1 ELLER påståendet (k^2+4)+3k^2+3k+1 -(k+1)^2 - 4 \ge 0). | 1 p. |
| k^2+4+3k^2+3k+1\geq k^2+2k+1+4=(k+1)^2+4 ELLER en sann olikhet härlett ur villkoret. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Startpoäng: Examinanden har testat att olikheten uppfylls för något värde k \ge 2. (Denna poäng kan också hittas i deluppgift 8.2 eller 8.3.) | 1 p. |
| Examinanden har bevisat induktionspåståendet utan att använda induktionsantagandet: 1+1+1+1+0+0 | max 4 p. |
| I induktionsantagandet oklart att det är fråga om något värde på variabeln k eller någon annan oklarhet i induktionens struktur. | –1 p. |
| Terminologin i induktionen behöver inte vara precis den ovanstående, om bara strukturen är klar. | –0 p. |
| Olikheten har bevisats utan att man använt induktion. | +0 p. |
| oberoende Då k<0, är k^3<0. | 1 p. |
| oberoende k^2+4>0 | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Exempel på något värde på k för vilken olikheten inte gäller. | +0 p. |
| Vi bildar funktionen f(x)=x^3-x^2-4 ELLER idé om derivering av två funktioner. | 1 p. |
| f'(x)=3x^2-2x ELLER jämförelse av två derivator 3x^2 och 2x. | 1 p. |
| Examinanden har visat att f'(x) \ge 0, då x \ge 2 (exempelvis med att derivatans nollställen är x=0 och x=\frac{2}{3} och funktionens teckenschema är i formen + | - | + ELLER f'(x)=x (3x-2) \ge 0, då x \ge 2). | 1 p. |
| Då x\geq 2 är funktionen alltså växande. Eftersom f(2)=0, är påståendet bevisat. | 1 p. |
| ELLER | |
| Division med talet x^2, som är positivt, dvs. man måste visa att x \ge 1+4/x^2. | 2 p. |
| Eftersom x\ge 2 \ge 1+\frac{4}{x^2} är detta klart. | 2 p. |
| ELLER | |
| x^3-x^2 = x^2 (x-1) \ge 4, då x \ge 2, | 2 p. |
| eftersom x^2 \ge 4 och x-1 \ge 1, då x \ge 2. | 1+1 p. |
| ELLER | |
| Funktionen f(x)=x^3-x^2-4 har bildats. | 1 p. |
| Nollställena har lösts ut och testpunkter har beräknats. | 1 p. |
| Funktionens förlopp har konstaterats. | 1 p. |
| Den ovan nämnda informationen har kombinerats och examinanden har konstaterat att olikheten gäller. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Endast Solve på olikheten och som svar x \ge 2. | 0 p. |
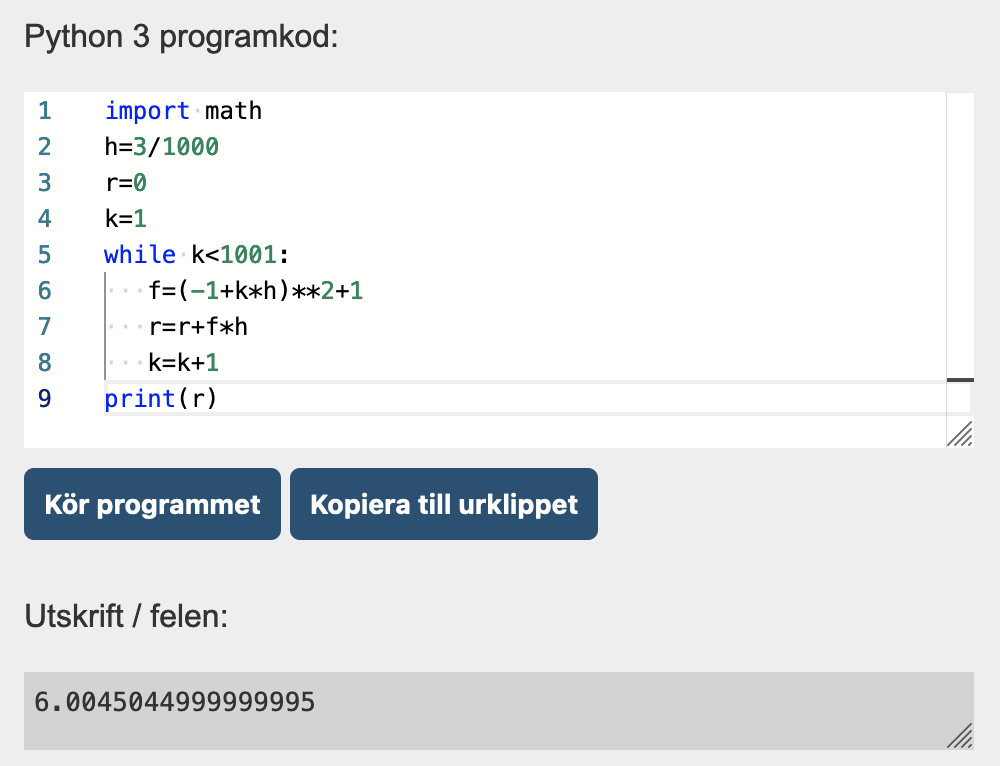
9. Integralalgoritm 12 p.
I text presenteras en algoritm skriven i pseudokodform.
Vilket resultat ger algoritmen då a=0, b=1 och n=5? (2 p.)
Gör en implementering av algoritmen med kalkylprogram eller med programmering, då a=-1, b=2 och n=1000. Vilket resultat ger algoritmen i det här fallet? (4 p.)
Vilken integral approximerar algoritmen? Förklara den roll variablerna a, b, n, h, r, k och f har i algoritmen. (6 p.)
| h=\frac{b-a}{n}=\frac{1-0}{5}=\frac{1}{5} | |
| k=1: f=(0+1\cdot\frac{1}{5})^2+1=\frac{26}{25}, r=0+\frac{26}{25}\cdot\frac{1}{5}=\frac{26}{125}. | 1 p. |
| k=2: f=(0+2\cdot\frac{1}{5})^2+1=\frac{29}{25}, r=\frac{26}{125}+\frac{29}{25}\cdot\frac{1}{5}=\frac{11}{25}. k=3: f=(0+3\cdot\frac{1}{5})^2+1=\frac{34}{25}, r=\frac{11}{25}+\frac{34}{25}\cdot\frac{1}{5}=\frac{89}{125}. k=4: f=(0+4\cdot\frac{1}{5})^2+1=\frac{41}{25}, r=\frac{89}{125}+\frac{41}{25}\cdot\frac{1}{5}=\frac{26}{25}. k=5: f=(0+5\cdot\frac{1}{5})^2+1=2, r=\frac{26}{25}+2\cdot\frac{1}{5}=\frac{36}{25}\ (=1\mathrm{,}44). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Endast korrekt svar ELLER endast svaret 1{,}04 (indexfel). | 1 p. |
| Noggrann förklaring på iterationen eller skärmdump av en Python-implementering eller en kalkylprogramimplementering räcker som motivering. | |
| Startpoäng: Beräknat f:s formel som endast beror av k ELLER beräknat värdena för funktionen f för varje 1\le k\le 5. | 1 p. |
| oberoende f:s iterationsformel förklarad, eller så är den synlig i förståelig form. | 1 p. |
| oberoende r:s iterationsformel förklarad, eller så är den synlig i förståelig form. | 1 p. |
| oberoende Korrekt svar 6\mathrm{,}005. Alla noggrannheter duger. | 1 p. |
| oberoende Python-koden är synlig eller en skärmdump av en kalkylprogramimplementering (åtminstone sista raden, se exemplet nedan). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Implementering av koden för allmänna värden på talen a, b och/eller n utan insättningar a=-1, b=2, n=1000. Poängavdrag från den första raden på vilken felet inverkar. | –1 p. |
| Allmänt fel: sista iterationen saknas. | max 3 p. |
| Exempelfigur på en lösning gjord med Python. | |
| Exempelfigur på en lösning gjord med kalkylprogram. | |
| Vi betecknar uttrycket i f-kolumnen =(–1+A3*$G$5)^2+1 och r-kolumnens uttryck =C2+B3*$G$5. Det betyder alltså att man i r-kolumnen adderar det föregående r-värdet och det nya f-värdet. | |
| Den sista raden ser ut så här: | |
| Värdet är alltså ungefär 6\mathrm{,}005. |
| Algoritmen approximerar värdet på integralen \int_{-1}^2(x^2+1)\,\mathrm{d}x och | |
| oberoende den funktion som ska integreras är x^2+1, | 1 p. |
| oberoende a är integrationsintervallets startpunkt och b integrationsintervallets slutpunkt, | 1 p. |
| oberoende n anger hur många delintervall integrationsintervallet delas in i (och arean på varje delintervall approximeras med en rektangel) och h är delintervallets längd, | 1 p. |
| oberoende r beräknar delsummans värde, dvs. till den variabeln adderas rektanglarnas areor, | 1 p. |
| oberoende k är värdet på indexet som anger vilken rektangel i ordningen som behandlas, | 1 p. |
| oberoende f anger värdet på den funktion som integreras. | 1 p. |
Del B2
10. Positronemissionstomografi 12 p.
Positronemissionstomografi (PET) är en medicinsk kameraundersökningsmetod med vilken man kan göra en modell av de inre organens funktion. Med hjälp av en PET-bild är det möjligt att bilda en tid-aktivitetskurva, som har formen f(t)=g(t)+u e^{v-(t-w)^2}, där u, v, w>0 och
g(t)= \begin{cases} 0, &\text{då } t<0,\\ a_1t+b_1, &\text{då } 0\le t<w,\\ a_2t+b_2, &\text{då } t\ge w. \end{cases}
Tabell innehåller mätningsvärden som funktion av tiden för en viss PET-bild. Man kan skapa en modell av mätningen med hjälp av funktionen f, då u=\frac15, v=3, w=2, a_1=\frac54, b_1=0, a_2=-\frac14 och b_2=3. Rita grafen av funktionen f samt mätningsvärdena i ett koordinatsystem. (4 p.)
Hur påverkar parametrarna u, v och w funktionens graf? (4 p.)
Vilka villkor ska parametrarna w, a_1, b_1, a_2 och b_2 uppfylla för att funktionen f ska vara kontinuerlig? (4 p.)
| Kurvan är delvis korrekt (två delar av en styckvis definierad funktion). | 1 p. |
| Kurvan är korrekt på ögonmått. | 1 p. |
| oberoende Punkterna är korrekta på ögonmått. | 1 p. |
| Korrekt uttryck och punkternas korrekta koordinater är insatta i programvaran på ett synligt sätt. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Punkterna är utplacerade på kurvan. | +0 p. |
| En polynomanpassning till punkterna eller spline. | +0 p. |
| Variabeln kan vara en annan än t. | –0 p. |
| Observera att det i den preliminära bedömningen inte nödvändigtvis beaktats att t<0 saknas. Poäng: (1+0+1+0). | max 2 p. |
| Punkterna och funktionen är ritade i olika koordinatsystem. | –0 p. |
| Startpoäng: Funktionen g är korrekt ritad. | 1 p. |
| Exempelfigur på en modellösning: | |
| Då u växer så höjs funktionens topp (eller största värdet ökar). | 1 p. |
| Då v växer så höjs funktionens topp (eller största värdet ökar). | 1 p. |
| Två väsentligt olika iakttagelser om parametern w (en poäng per iakttagelse). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Exempel på iakttagelser gällande parametern w: Parametern w inverkar på funktionens kontinuitet.”, Parametern w inverkar på placeringen av toppen i t-riktning.”, ”Parametern w bestämmer när uttrycket byts i funktionen.” | |
| ”Parametrarna u och v förändrar toppens höjd.” För de två första raderna sammanlagt | 1 p. |
| Klart fel observation vid ett ställe för vilket poäng ges, av deluppgiften totalt: | –1 p. |
| En del onödig information (exempelvis vad som händer då u<0). | –0 p. |
| Skärmdump med en negativ parameter eller ett annat fel. | –0 p. |
| Startpoäng: Examinanden har prövat hur olika parametrar inverkar med exempelvis en glidare. | 1 p. |
| oberoende Examinanden har konstaterat att funktionen är kontinuerlig i övriga punkter än t = 0 och t = w. | 1 p. |
| Jämförelse av uttryck i brytningspunkterna t = 0 och t = w. | (1 p.) |
| Slutsatserna b_1 = 0 och b_2 = w(a_1 - a_2). | 1 p. |
| Examinanden har korrekt tillämpat definitionen för kontinuitet i punkterna t = 0 och t = w. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Ekvationen b_2 = w(a_1 - a_2) i vilken form som helst godkänns. | –0 p. |
| Endast kontinuiteten hos funktionen g har granskats utan att man explicit konstaterat att det räcker för att funktionen f ska vara kontinuerlig. | –1 p. |
11. Lärdom av tärningskast 12 p.
Erin vill välja den bättre av två tärningar. Hen kastar dem en gång och väljer den tärning som ger det större resultatet. Om båda tärningarna ger samma resultat väljer hen en av tärningarna. I båda fallen kastar Erin den tärning hen valt en gång till. Med vilken sannolikhet är tärningens resultat mindre på det andra kastet än på det första kastet? (9 p.)
Enligt en nyhet som fått stor spridning fördubblades förmögenheten hos de tio rikaste personerna i världen under de två första åren av coronapandemin. Påståendet grundar sig av allt att döma på att man i slutet av tidsperioden hade beräknat värdet på förmögenheten hos de tio rikaste personerna och jämfört detta med deras förmögenhet två år tidigare. I det här ingår ett tankefel som också framkommer i Erins tärningskast. Vilket är tankefelet? (3 p.)
| I samband med att den bättre tärningen avgörs (se specifika anvisningar för deluppgiften) har examinanden konstaterat att det vid ett kast med två tärningar finns 36 alternativ ELLER sannolikheten för utfallen är \frac1{36}. | 1 p. |
| Det största ögontalet och antalet fall som motsvarar detta är korrekt: 6|11, 5|9, 4|7, 3|5, 2|3 ja 1|1. (1 p. om två är korrekta.) | 2 p. |
| oberoende Antalet fall är motiverat med en förklaring eller med en figur. | 2 p. |
| oberoende Om det större ögontalet är k‚ är sannolikheten för att man kastar fram ett mindre värde i följande omgång \frac{k-1}{6}. (1 p., om något fall är korrekt ELLER om antalet gynnsamma fall är k-1.) | 2 p. |
| Svaret beräknat på egna tal med korrekt logik (se specifika anvisningar för deluppgiften) (korrekt beräkning \frac{11}{36} \cdot \frac{5}{6} + \frac{9}{36} \cdot \frac{4}{6} +\frac{7}{36} \cdot \frac{3}{6} +\frac{5}{36} \cdot \frac{2}{6} + \frac{3}{36} \cdot \frac{1}{6} = \frac{125}{216} \approx 0{,}579). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Man får ge svaret i decimalform; 0{,}6 eller noggrannare duger. | |
| Man får inte poängen för rad 1 om de 36 utfallen härleds från det att man beräknar sannolikheter för ett nytt kast (rad 4), jfr. nedanstående max 3-fall. | |
| Med ”korrekt logik” på rad 5 avses en beräkning i formen \sum_k p(k)p(A|k). Om alla sannolikheter p(k) är lika, för denna rad 1 p. | |
| För tolkningen ”mindre eller lika stor” på rad 4 och motsvarande sannolikhet \frac{k}6. (1+2+2+1+2) | max 8 p. |
| Man har först kastat endast en tärning och beräknat \frac1{6} (\frac56 + \frac46 + \frac36 +\frac26 + \frac16) = \frac{5}{12}. (0+0+0+2+1) | max 3 p. |
| Man har först kastat endast en tärning, med en 6\times 6 tabell beräknat 15 gynnsamma fall och fått \frac{15}{36} eller \frac{5}{12} som svar (0+0+0+1+1) | max 2 p. |
| Korrekt programkod 8 p. och förklaring 1 p. |
| En trovärdig observation om förändringen av förmögenheten hos de 10 rikaste personerna (exempelvis: ”Den sammanlagda förmögenheten hos de tio rikaste personerna kan fördubblas, fast förmögenhetens värde för en del av dem skulle minska”). | (1 p.) |
| Samma människor tillhörde nödvändigtvis inte de 10 rikaste för två år sedan. | 1 p. |
| oberoende Ju mera förmögenheten växer desto mer sannolikt är det att man hamnar på listan över de 10 rikaste personerna ELLER presenterat en förnuftig analogi mellan de 10 rikaste personerna och Erins tärningskast. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Exempel på ett svar som värt 3 poäng: ”Bland de tio rikaste personerna är sannolikt de vilkas förmögenhet ökat på ett betydande sätt under två år, och inte de vars egendom har ökat mindre.” | |
| Tilläggsinformation: I uppgiften behandlas fenomenet ”regression towards the mean”. I det här fallet framgår det på följande sätt. I båda fallen väljs den grupp som undersöks utgående från det att den undersökta variabelns värden är stora. Om variabelns värde är stort av en slump (som i tärningskastet) så minskar den mera sannolikt. Bland de rikaste personerna betyder det att de, vilkas förmögenhet är stor då listan görs, mer sannolikt är sådana vilkas förmögenhet minskar mer än vanligt då man går bakåt i tiden. Med andra ord är de sådana som har sett värdet av sin förmögenhet öka mer än vanligt. |
12. Polynomkonstruktion 12 p.
Ge ett exempel på ett polynom P(x) som uppfyller följande villkor:
Ekvationen P(x)=1 har exakt två olika stora lösningar, och ekvationen P(x)=-1 har åtminstone fyra olika stora lösningar.
En lösning som ger fulla poäng innehåller sådana uträkningar av vilka man kan se att exemplet uppfyller de villkor som krävs. Enbart en grafisk motivering eller användning av ett ekvationslösningskommando räcker inte till för att få fulla poäng.
| Examinanden har som svar gett ett polynom av minst fjärde graden ELLER konstaterat att man utgår från att ett polynom av minst fjärde graden ska hittas ELLER en polynomfamilj av minst fjärde graden, vars koefficienter man försöker bestämma. | 1 p. |
| I svaret undersöks ekvationerna P(x)=1 och P(x)=-1 algebraiskt eller grafiskt ELLER man undersöker funktionens förlopp (exempelvis med ett ogrundat teckenschema) ELLER grafen av ett polynom ritat med programvara, och utifrån figuren kan man på ögonmått se att det givna polynomet uppfyller de villkor som krävs. | 1 p. |
| Examinanden har visat att ekvationen P(x)=1 har exakt två lösningar OCH att ekvationen P(x)=-1 har åtminstone fyra lösningar. Precisering av poängutdelningen för vardera ekvationen nedan. | 5+5 p. |
| Allmänna drag i poängutdelningen: | |
| P(x)=-1: 2 p. för den första lösningen, 1 p./lösning för de återstående | 0+5 p. |
| P(x)=1 har åtminstone två olika stora reella lösningar 2 p./ högst två olika stora reella lösningar 3 p. | 5+0 p. |
| Mer noggrann poängutdelning (poängen ges enligt den rad som ger de bästa poängen): | |
| Närmevärdeslösning med programvara för en ekvation av minst fjärde graden ELLER en grafisk lösning (lösningarna är utmärkt ens på ögonmått) ELLER man har endast beräknat derivatans nollställen och bildat ett teckenschema. | 1 p. |
| En noggrann lösning med programvara för en ekvation av minst fjärde graden. | 2 p. |
| Man har med programvara löst en ekvation av högre än tredje graden i mellansteg. | 3 p. |
Matematiskt motiverad slutledning där följande godkänns:
| 5 p. |
| Specifika anvisningar för uppgiften | |
| Poängen i poängraden 5+5 kan man bara få om man försöker få båda villkoren att uppfyllas för samma polynom (dvs. i allmänhet kan man inte få 0+5 eller 5+0). | |
| Konstruktiva lösningar bedöms enligt samma anvisningar och poängfördelning. | |
| I konstruktionen har man tilldelat funktionen och derivatan värden utan en utskriven förklaring på varför de garanterar de villkor som krävs (P(x)=1 och P(x)=-1) (ur båda villkoren skilt -1 poäng). | max 11 p. |
| Som svar två olika polynom, ett för vardera villkor. | 0 p. |
| Man har löst linjära ekvationssystem och andragradsekvationer med programvara. | –0 p. |
| Ekvationer har lösts med programvara i kontrollsyfte. | –0 p. |
| Polynomet har erhållits genom anpassning till punkterna. | +0 p. |
| Startpoäng: Situationen har åskådliggjorts grafiskt med en graf samt med linjerna y=1 och y=-1 (polynomets uttryck saknas eller är felaktigt). Om svaret inte behandlar ett polynom av minst fjärde graden så ges inte övriga poäng för uppgiften. | 1 p. |
13. Ändring av ordningsföljden på integral och gränsvärde 12 p.
Anta att \displaystyle f(x,s)=\frac{1-s}{(1+x^2-2sx)^2}, då 0<s<1 och 0\le x\le 1. Vi granskar det vänstersidiga gränsvärdet \displaystyle\lim_{s\to 1}, som ibland betecknas \displaystyle\lim_{s\to 1^-}.
Bestäm \displaystyle g(x)=\lim_{s\to 1} f(x,s) för alla 0\le x<1, och beräkna \displaystyle \int_0^1 g(x)\, dx. (3 p.)
Bestäm ett sådant x_0<1, att f(x_0, s) = f(1, s), och beräkna \displaystyle \int_{x_0}^1 f(x_0,s)\, dx. (3 p.)
Visa att f(x, s) \ge f(x_0, s), då x\in [x_0, 1] och x_0 är definierat i deluppgift 13.2. (3 p.)
Visa att \displaystyle \int_0^1 \lim_{s\to 1} f(x,s)\, dx \ne \lim_{s\to 1} \int_0^1 f(x,s)\, dx. (3 p.)
| Examinanden försöker beräkna gränsvärdet i rätt punkt och med avseende på rätt variabel. | 1 p. |
| g(x)=\lim_{s\rightarrow 1}f(x,s)=\lim_{s\rightarrow 1}\frac{1-s}{(1+x^2-2sx)^2}=0 (då 0\leq x<1). | 1 p. |
| Därmed är \int_0^1g(x)\,\mathrm{d}x=0. | 1 p. |
| Specifika anvisningar för denna lösning | |
| Tilläggsinformation: Då x=1, är \lim_{s\rightarrow 1}f(x,s)=\lim_{s\rightarrow 1}\frac{1-s}{(1+1^2-2s\cdot1)^2}=\infty. |
| Vi löser ekvationen \frac{1-s}{(1+x^2-2sx)^2}=\frac{1-s}{(1+1^2-2s\cdot1)^2}. Eftersom i nämnarna 2-2s>0 och h(x,s)=1+x^2-2sx>1+x^2-2x=(1-x)^2\geq 0, kan ekvationen förenklas till formen x^2-2sx=1-2s, som kan skrivas som produkten (1-x)(x+1-2s)=0. | 1 p. |
| Nu är x=1 eller x=2s-1. Det efterfrågade värdet är alltså x_0=2s-1, och funktionens värde i denna punkt är f(2s-1,s)=f(1,s)=\frac{1-s}{(2-2s)^2}. | 1 p. |
| Integralen är \int_{x_0}^1\frac{1-s}{(2-2s)^2}\,\mathrm{d}x=\frac{1-s}{(2-2s)^2}(1-x_0)=\frac{1-s}{(2-2s)^2}(1-(2s-1)) =\frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| För ett fast s är h(x,s)=x^2+1-2sx en uppåtvänd parabel och h(x_0,s)=h(2s-1,s)=(2s-1)^2+1-2s(2s-1)= -2s+2 =h(1,s), dvs. h(x,s)\leq h(x_0,s) för varje x\in [x_0,1]. | 1 p. |
| Eftersom dessutom h(x,s)=x^2-2 s x +1 >(1-x)^2\geq 0, är h(x,s)^2\leq h(x_0,s)^2 för varje x\in [x_0,1]. | 1 p. |
| Eftersom f(x)=\frac{1-s}{h(x,s)}, så är f(x,s)\geq f(x_0,s) för varje x\in [x_0,1]. | 1 p. |
| Vi uppskattar \lim_{s\rightarrow 1}\int_0^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1}\int_{x_0}^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1} \frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| Nu är gränsvärdena olika stora eftersom \int_0^1\lim_{s\rightarrow 1}f(x,s)\,\mathrm{d}x=\int_0^1g(x)\,\mathrm{d}x=0. | 2 p. |
| ELLER lösningar gjorda med programvara |
| Vi definierar korrekt den funktion som ska undersökas f(x,s):=\frac{1-s}{(1+x^2-2\cdot x \cdot s)^2 } och g(x)=\lim_{s\rightarrow 1-}f(x,s) av vilket g(x)=0 (då 0\leq x<1) | 2 p. |
| Därmed är \int_0^1g(x)\,\mathrm{d}x =0. I den här punkten måste funktionen f vara korrekt definierad och g har erhållits som ett vänstersidigt gränsvärde. | 1 p. |
| Specifika anvisningar för denna lösning | |
| Om gränsvärdet inte är vänstersidigt ELLER uttrycket för funktionen g inte syns (ens i formen \lim f = 0, g=\lim f). | 1+1 p. |
| Om man inte satt ut ett multiplikationstecken så kan programvaran tolka produkten xs som variabeln xs. I den här deluppgiften framgår inte felet tydligt. Därför inget avdrag i den här deluppgiften, men med denna definition får examinanden inga poäng i fortsättningen. | –0 p. |
| \mathrm{solve}(f(x_0,s)=f(1,s),x_0), av vilket x_0=\pm\sqrt{s^2+2 s-3} +s, \ x_0=2s-1, \ x_0=1. | 1 p. |
| Av dessa duger endast x_0=2s-1 eftersom x_0<1 och radikanden är negativ i det granskade intervallet, eftersom \mathrm{solve}(s^2+2s-3<0,s), av vilket -3<s<1. | 1 p. |
| \int_{2s-1}^1 f(2s- 1, s ) \, dx = \frac{1}{2}. | 1 p. |
| Specifika anvisningar för denna lösning | |
| Fel definition leder till ”lösningarna” x_0= \pm\sqrt{4sx-3}, \ x_0=\pm 1. | 1 p. |
| På ett överensstämmande sätt kan man undersöka funktionen g(x,s):=f(x,s)-f(2s-1,s). Vi bestämmer derivatan k(x,s):=\frac{d}{dx} g(x,s)=\frac{4(s-1)(s-x)}{(2\cdot s \cdot x-x^2-1)^3}, nollställen \mathrm{solve}(k(x,s)=0,x), av vilket x=s eller s=1, | 1 p. |
| s tillhör det intervall som granskas, eftersom \mathrm{solve}(2s-1\leq s \leq 1,x), av vilket s\leq 1. | 1 p. |
| Eftersom g(2 s-1,s)=0 och g(s,s)=\frac{s+3}{4\cdot(s+1)^2}, är differensens minsta värde 0 och olikheten gäller. | 1 p. |
| Specifika anvisningar för denna lösning | |
| De lösningar x_0 som en felaktig definition ger är inte meningsfulla i den här deluppgiften. | 0 p. |
| Vi uppskattar \lim_{s\rightarrow 1}\int_0^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1}\int_{x_0}^1f(x,s)\,\mathrm{d}x\geq \lim_{s\rightarrow 1} \frac{2(1-s)^2}{(2-2s)^2}=\frac{1}{2}. | 1 p. |
| Nu är gränsvärdena olika stora eftersom \int_0^1\lim_{s\rightarrow 1}f(x,s)\,\mathrm{d}x=\int_0^1g(x)\,\mathrm{d}x=0. | 2 p. |