Hyvän vastauksen piirteet: FI – Fysiikka
24.3.2023
Lopulliset hyvän vastauksen piirteet 16.5.2023
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
Osa 1: 20 pisteen tehtävä
1. Täydennystehtäviä fysiikan eri osa-alueilta 20 p.
Alla on 10 täydennystehtävää (1.1–1.10). Valitse kussakin kohdassa pudotusvalikosta tilanteeseen parhaiten soveltuva vaihtoehto. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 Täydennä virke. 2 p.
- yhtä suuri (2 p.)
1.2 Täydennä virke. 2 p.
- kiihtyvässä liikkeessä (2 p.)
1.3 Täydennä virke. 2 p.
- liikemäärän (2 p.)
1.4 Täydennä virke. 2 p.
- skalaarisuure (2 p.)
1.5 Täydennä virke. 2 p.
- nousee (2 p.)
1.6 Täydennä virke. 2 p.
- samanmerkkiset (2 p.)
1.7 Täydennä virke. 2 p.
- pitkittäisenä (2 p.)
1.8 Täydennä virke. 2 p.
- vaihtojännitteen suuruutta (2 p.)
1.9 Täydennä virke. 2 p.
- \alpha (2 p.)
Ionisaation määrä ohuessa metallikalvossa riippuu kolmesta tekijästä, säteilyn lajista, säteilyn intensiteetistä ja säteilyn energiasta. Näistä intensiteetti ja energia ovat säädettäviä suureita ja valitsemalla yhden säteilylajin kohdalla intensiteetti tai energia suureksi ja muiden kohdalla pieneksi, saadaan suurin annos halutusta säteilystä. Koska näin voidaan toimia kaikkien säteilylajien kohdalla, oikeaa ratkaisua etsiessä tulee osata sivuuttaa intensiteetin ja energian vaikutus ja tarkastella säteilylle tyypillistä ionisointikykyä.
1.10 Täydennä virke. 2 p.
- infrapuna-alueella (2 p.)
Osa 2: 15 pisteen tehtävät
2. Ariane 5 -kantoraketti 15 p.
2.1 Laadi graafinen esitys raketin vauhdista ajan funktiona. Laadi esitys siten, että siinä näkyvät aineiston pisteet ja että siitä voi lukea raketin vauhdin millä tahansa ajanhetkellä aikavälillä 0 s – 1 500 s. 5 p.
Pisteytys:
On esitetty kuvaaja, jossa mitatut vauhdin arvot ajan funktiona näkyvät erillisinä mittauspisteinä. Esityksessä tulee näkyä mittauspisteiden kautta kulkeva yhtenäinen viiva, jolta vauhdin voi lukea millä ajanhetkellä tahansa. Yhtenäinen viiva saadaan parhaiten splini-interpolaatiolla, mutta tässä aineistossa mittauspisteet yhdistävä murtoviiva toimii myös hyvin (5 p.). Puuttuvasta tai pisteistöön sopimattomasta viivasta vähennetään 2 pistettä. Jos mittauspisteet eivät näy erillisinä pisteinä, vähennetään 2 pistettä.
Jos suureen tunnus puuttuu tai yksikkö puuttuu tai akselit ovat väärin päin, vähennetään kustakin virheestä 1 piste.
Tyypillinen virhe:
On piirretty mittauspisteisiin sovitettu funktio, joka ei kulje mittauspisteiden kautta.
2.2 Kuinka pitkän matkan raketti kulki radallaan aikavälillä 0 s – 1 500 s? 5 p.
Pisteytys:
Ratkaisusta käy ilmi, että matkan määrittämiseen on käytetty graafista integrointia (2 p).
Annettu vastauksena 2-3 merkitsevän numeron tarkkuudella matka välillä 9400 km – 9800 km (3 p). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillinen virhe:
On laskettu kuljettu matka suureyhtälöllä s = vt käyttäen jotain nopeutta ja aikaa.
2.3 Kuinka suuri oli raketin kiihtyvyys radallaan aikavälillä 700 s – 1 400 s? 5 p.
Pisteytys:
Ratkaisussa on kerrottu, että raketti on tasaisesti kiihtyvässä liikkeessä tarkasteltavalla aikavälillä, tai ratkaisussa on esitetty välille 700 s – 1400 s sovitettu suora, jonka kulmakerrointa on käytetty ratkaisussa (2 p).
Annettu vastauksena 2-3 merkitsevän numeron tarkkuudella kiihtyvyys välillä 2,4 m/s2 – 2,8 m/s2 (3 p). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillinen virhe:
On käytetty hetkellistä kiihtyvyyttä tai keskikiihtyvyyttä.
3. Lämmönsiirtokoneet 15 p.
Valitse lämmönsiirtokoneisiin liittyvissä osatehtävissä 3.1–3.8 vastaus, joka kuvaa tilannetta parhaiten fysikaalisesti.
Monivalintatehtävä ei ole pakollinen, ja siihen voi jättää vastaamatta. Vastattuasi osatehtävään voit vaihtaa vastausvaihtoehtoa, mutta et voi jättää osatehtävää enää kokonaan ilman vastausta. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää sitä arvosteltavaksi, valitse jokaisessa osatehtävässä vaihtoehto ”En vastaa”.
Osatehtävissä 3.1–3.3 tarkastellaan ilmalämpöpumppua, jolla siirretään energiaa kylmemmästä ulkoilmasta rakennuksen sisälle lämpimämpään ilmaan. Laitteessa on sisäyksikkö ja ulkoyksikkö, joiden välillä kiertää lämpöä siirtävä aine.
3.1 Miksi energian siirtyminen kylmästä ulkoilmasta lämpöä siirtävään aineeseen on mahdollista ulkoyksikössä? 1 p.
- Aine on kylmempää kuin ulkoilma. (1 p.)
3.2 Mitä lämpöä siirtävälle aineelle tapahtuu, kun se on höyrystimessä? 2 p.
- Aine höyrystyy ja ottaa vastaan energiaa ympäristöstä. (2 p.)
3.3 Lämpöpumpun sähköteho on 1 000 W. Oikea suuruusluokka lämpöpumpun lämmitysteholle on 2 p.
- 3 000 W (2 p.)
3.4 Jääkaappi tarvitsee toimiakseen sähköenergiaa. Mitä tapahtuu jääkaapin sähkönkulutukselle, jos huoneen lämpötila pysyvästi nousee? 2 p.
- Sähkönkulutus nousee. (2 p.)
3.5 Käynnissä olevan jääkaapin ovi unohdetaan auki pitkäksi aikaa. Mitä huoneen lämpötilalle tapahtuu? 2 p.
- Lämpötila nousee. (2 p.)
3.6 Mikä seuraavista kaavioista esittää lämmönsiirtokoneen toimintaperiaatetta? Kaavion nuolet esittävät suuntaa, johon energia siirtyy, ja keltainen laatikko esittää itse konetta. 2 p.
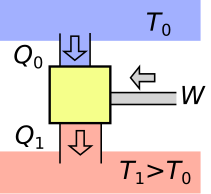 (2 p.)
(2 p.)
3.7 Mikä seuraavista graafeista esittää ideaalisen lämmönsiirtokoneen toimintaa? Aine on tässä tilanteessa koko ajan kaasua. 2 p.
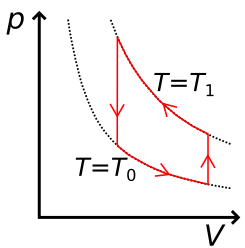 (2 p.)
(2 p.)
3.8 Eräässä ideaalisen lämmönsiirtokoneen työvaiheessa aineeseen tehdään työtä, mutta sen ja ympäristön välillä ei siirry lämpöä. Aine pysyy kaasuna koko tämän työvaiheen ajan. Mitä kaasun lämpötilalle ja tilavuudelle tapahtuu? 2 p.
- Kaasun lämpötila kasvaa ja tilavuus pienenee. (2 p.)
Ruotsinkielisessä kokeessa olleen virheen vuoksi ruotsinkielisessä kokeessa hyväksytään myös vastaus ”Kaasun lämpötila pysyy samana ja tilavuus pienenee.
4. Kondensaattori 15 p.
4.1 Kuvassa on esitetty kondensaattorilevyjen välinen jännite ajan funktiona. Täydennä kuvan keskeneräinen kytkentäkaavio siten, että piirillä voisi tuottaa kuvan mukaisen kuvaajan. Käytä kahta kytkintä, johtimia, vastusta sekä jännitemittaria. Voit hyödyntää komponenttien kuvia , ja . Selitä, miten mittaus toteutetaan täydentämälläsi piirikaaviolla ja missä järjestyksessä kytkimiä suljetaan tai avataan. 8 p.
Kuvasta 4.A havaitaan, että kondensaattorin jännite ei muutu äkillisesti vaan eksponentiaalisesti. Tämän saa aikaan kondensaattorin kanssa sarjassa oleva vastus. Koska varaamiseen ja purkamiseen kuluu yhtä paljon aikaa, vastuksen on oltava sama kummassakin tapauksessa. Tällä perusteella rakennetaan oheinen kytkentä, jossa näkyvät vastuksen, kytkimien ja jännitemittarin paikat.
Kondensaattorin varaamiseksi suljetaan kytkin 1. Tämän jälkeen avataan kytkin 1 ja suljetaan kytkin 2, jolloin kondensaattori purkautuu. Jännitemittarilla voidaan havaita potentiaaliero kondensaattorin yli.
Pisteytys:
Komponentit on kytketty siten, että kytkimiä sulkemalla tai avaamalla on mahdollista saada kuvan 4.A mukainen kondensaattorin latautuminen (2 p) ja purkautuminen (2 p).
Kytkimien käyttö on kuvattu siten, että saadaan kuvan 4.A mukainen latautuminen (2 p) ja purkautuminen (2 p).
Mikäli jännitemittari on kytketty mittaamaan jotain muuta kuin kondensaattorin yli olevaa jännitettä, osiosta ei anneta pisteitä.
Tyypillinen virhe:
On kytketty vastus kytkimen 2 kanssa sarjaan, jolloin kondensaattori latautuu paljon pienemmällä aikavakiolla kuin purkautuu. Tällaisesta ratkaisusta voi saada korkeintaan 4 pistettä.
4.2 Onko virran suunta kuvan pisteessä P ylös- vai alaspäin varautumiskäyrän ajanhetkillä t1 ja t2? 4 p.
Hetkellä t1 kondensaattori varautuu ja virran suunta on kuvassa alaspäin. Hetkellä t2 kondensaattori purkautuu ja virran suunta on ylöspäin.
Pisteytys:
On kytketty oikea suunta annetuista suuntavaihtoehdoista oikeaan ajanhetkeen t1 (2 p.) ja t2 (2 p.).
4.3 Miten muuttaisit piirin komponentteja, jos haluat hidastaa kondensaattorin varautumista ja purkautumista? 3 p.
Varautumis- ja purkautumisnopeutta voidaan hidastaa käyttäen vastusta, jolla on suurempi resistanssi, tai kondensaattoria, jolla on suurempi kapasitanssi. Huippujännite määräytyy edelleen jännitelähteen avoimen piirin napajännitteestä.
Pisteytys:
On kerrottu joko kapasitanssin kasvattaminen, resistanssin kasvattaminen tai toisen vastuksen lisääminen sarjaan (3 p.).
Tyypillinen virhe:
On kerrottu, että lisätään toinen vastus mainitsematta, miten se kytketään.
5. Kynttilä 15 p.
Kynttilää poltetaan ja sen pituus mitataan palamisajan funktiona. Mittausten tulos on esitetty aineistossa . Kynttilän pituus alussa on 189 mm, halkaisija on 21 mm ja keskimääräinen tiheys on 862 kg/m3.
5.1 Laadi graafinen esitys kynttilän pituudesta ajan funktiona. Esitä graafissa aineiston pisteet ja mittausaineistoon sopiva malli. 5 p.
Malliksi saadaan suora, jonka yhtälö on L(t) = 178mm - 0,37 t mm/min.
Malli sopii mittausaineistoon hyvin, paitsi aivan alussa, jossa kynttilän halkaisija ei ole vakio.
Pisteytys:
On laadittu graafinen esitys, jossa mitatut pituuden arvot ajan funktiona näkyvät erillisinä mittauspisteinä. (3 p.). On esitetty mallina kuvaan piirretty suora yhtenäisellä viivalla ja annettu suoran yhtälö (2 p.).
Jos kuvassa on esitetty useampi yhtenäinen viiva, niistä huonoin luetaan malliksi.
Jos mittauspisteet eivät näy erillisinä pisteinä, vähennetään 2 pistettä.
Jos suureen tunnus puuttuu tai yksikkö puuttuu tai akselit ovat väärin päin, vähennetään kustakin virheestä 1 piste.
Tyypillinen virhe:
On yhdistetty pisteet murtoviivalla tai sovitettu jokin muu funktio kuin suora.
5.2 Toinen samanlainen kynttilä poltetaan täynnä vettä olevassa maljakossa, jossa kynttilä kelluu, kuten aineistossa näkyy. Jotta kynttilä pysyisi pystyssä, sen tyveen kiinnitetään painoksi metallirengas, jonka massa on 3,5 g. Voit olettaa renkaan tilavuuden pieneksi. Kuinka kauan kynttilä palaa maljakossa? Voit hyödyntää aineiston voimakuviota ja osatehtävässä 5.1 tekemääsi graafista esitystä. 10 p.
Kynttilään vaikuttavat voimat ovat kynttilän ja metallirenkaan yhteenlaskettu paino G ja noste N. Koska kynttilä kelluu, voimat ovat tasapainossa, G-N=0.
Kynttilän massa saadaan sen pituuden L, halkaisijan D ja tiheyden \rho_k avulla. Kun renkaan massa on m, kynttilän ja renkaan yhteenlasketuksi massaksi saadaan
M=\rho_k\frac{\pi D^2}{4}L+m.Kynttilän pituudesta L veden pinnan alla on pituus h. Nosteen suuruus on kynttilän syrjäyttämän veden painon suuruinen. Kynttilän syrjäyttämän vesimäärän tilavuus on V_v=h\frac{\pi D^2}{4} , joten nosteen suuruus on \rho_v\frac{\pi D^2}{4}hg , jossa \rho_v on veden tiheys. Havaitaan, että sekä G että N muuttuvat ajan funktiona.
Yhdistämällä nämä voimatasapainon kanssa saadaan \Bigl(\rho_k\frac{\pi D^2}{4}L+m\Bigr)g=\rho_v\frac{\pi D^2}{4}hg.
Kynttilän palaessa sen pituus pienenee. Kynttilä jää kokonaan pinnan alle, kun kynttilän ja renkaan yhteenlaskettu paino on suurempi kuin noste. Tällöin L = h ja tasapainoyhtälöstä saadaan \Bigl(\rho_k\frac{\pi D^2}{4}L+m\Bigr)g=\rho_v\frac{\pi D^2}{4}Lg ja edelleen L=\frac{4m}{\pi D^2(\rho_v-\rho_k)}\approx {\rm 73,2}\,{\rm mm}.
Graafisesta esityksestä lukemalla tämä tapahtuu 280 minuutin kohdalla.
Pisteytys:
On esitetty Newtonin II lailla perusteltu skalaari- tai vektorisuureiden avulla kirjoitettu suureyhtälö kynttilään vaikuttaville voimille (2 p.).
On esitetty oikeat suureyhtälöt kynttilän painolle käyttäen kynttilän ja renkaan yhteenlaskettua massaa (2 p.) ja nosteelle mainiten tiheydeksi veden tiheys (2 p.).
On annettu vastauksena 2-3 merkitsevän numeron tarkkuudella paloajaksi 270 min – 280 min (4 p.). Muusta tarkkuudesta vähennetään 1 piste. Kynttilän uppoamispituutta ei arvostella, mutta mikäli lopputulos on väärin, oikeasta uppoamispituudesta voi saada 2 pistettä.
Tyypillisiä virheitä:
Vektoreiden ja skalaarien sekoittaminen yhtälön sisällä, nosteen määrittäminen parafiinin tiheyttä käyttäen, kynttilän lyhenemisen unohtaminen joko painon tai nosteen lausekkeesta.
6. Sipsipussin rapistelu 15 p.
Yhdysvaltalainen yritys toi vuonna 2010 markkinoille biohajoavan Sun Chips -perunalastupussin. Pussin ongelmana oli voimakas rapisteluääni, jonka intensiteettitaso ylsi peräti 95 desibeliin. Oletetaan, että intensiteettitaso mitattiin 1,0 metrin etäisyydeltä.
6.1 Mikä on intensiteettitaso, kun viisi ihmistä rapistelee kukin omaa sipsipussiaan samanaikaisesti 1,0 metrin etäisyydellä mittarista? 4 p.
Äänen havaittua voimakkuutta kuvaa intensiteettitaso L=10\,{\rm dB}\cdot\log\frac{I}{I_0} , jossa I on havaittu intensiteetti ja I_0=10^{-12}\,{\rm W/m}^{2} ihmisen kuulokynnystä vastaava intensiteetin vertailutaso.
Yhden pussin rapistelun intensiteettitaso metrin etäisyydellä on L=10\,{\rm dB}\cdot\log\frac{I_p}{I_0}={\rm 95}\,{\rm dB} , jossa I_p on rapistelun intensiteetti.
Tästä saadaan rapistelun intensiteetiksi I_p=10^{9,5}I_0=10^{-2,5}\,{\rm W/m}^2.
Jos rapistelijoita on viisi, intensiteetti on viisinkertainen eli 5 I_p=5\cdot 10^{-2,5}\,{\rm W/m}^2.
Tällöin intensiteettitaso on L={\rm 10}\,{\rm dB}\cdot\log\frac{5\cdot 10^{-2,5}\,{\rm W/m}^2}{10^{-12}\,{\rm W/m}^{2}}={\rm 102}\,{\rm dB}\approx {\rm 100}\,{\rm dB}.
Pisteytys:
On annettu 1-3 merkitsevän numeron tarkkuudella intensiteetin viisinkertaistumisen avulla laskettu intensiteettitaso 100 dB – 102 dB (4 p.). Muusta tarkkuudesta vähennetään 1 piste.
Ruotsinkielisessä kokeessa hyväksytään oikeaksi vastaukseksi edellisen lisäksi intensiteetin viisinkertaistumisen avulla laskettu intensiteetti.
Tyypillinen virhe:
On kerrottu yhden pussin intensiteettitaso viidellä.
6.2 Tuotekehityksellä rapisteluäänen intensiteettitaso saatiin laskettua 75 desibeliin. Kuinka monta prosenttia äänen intensiteetti oli tällöin alkuperäisestä intensiteetistä? 3 p.
Intensiteettitason suureyhtälöstä nähdään, että intensiteetin kymmenkertaistuessa intensiteettitaso kasvaa 10 dB:llä ja intensiteetin satakertaistuessa intensiteettitaso kasvaa 20 dB:llä. Vastaavasti on niin, että jos intensiteettitaso pienenee 20 dB, intensiteetti pienenee sadasosaan. Tuotekehityksen jälkeen rapisteluäänen intensiteetti on siis 1,0 % alkuperäisestä intensiteetistä.
Pisteytys:
On annettu 1-2 merkitsevän numeron tarkkuudella vastaus 1 % (3 p.). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillinen virhe:
On verrattu intensiteettitasoja intensiteettien sijaan.
6.3 Arvioi, millä etäisyydellä alkuperäisen sipsipussin intensiteettitaso (95 dB) vastaa tuulen huminaa, jonka intensiteettitaso on 30 dB. 5 p.
Tuulen huminan intensiteettitaso voidaan kirjoittaa muodossa L_t=10\,{\rm dB}\cdot \log\frac{I_t}{I_0}=30\,{\rm dB}.
Tästä saadaan huminan intensiteetiksi I_t=10^3I_0=10^{-9}\,{\rm W/m}^{2}.
Intensiteetti on kääntäen verrannollinen etäisyyden neliöön. Tällöin \frac{I_p}{I_t}=\frac{r_t^2}{r_p^2} , josta voidaan ratkaista etäisyydeksi r_t=r_p\sqrt{\frac{I_p}{I_t}}={\rm 1,0}\,{\rm m}\,\sqrt{\frac{10^{-2,5}\,{\rm W/m}}{10^{-9}\,{\rm W/m}}}={\rm 1}\,{\rm 778,3}\,{\rm m}\approx {\rm 1,8}\,{\rm km.}
Pisteytys:
Ratkaisusta käy ilmi intensiteetin 1/r2 -riippuvuus geometrian perusteella (2 p.).
On annettu 2-3 merkitsevän numeron tarkkuudella etäisyys 1,8 km (3 p.). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillinen virhe:
Perusteltu intensiteetin pieneneminen suureyhtälöllä I = \frac{P}{A}, missä A on ympyrän pinta-ala.
6.4 Miksi osatehtävässä 6.3 laskettu etäisyyden arvio ei ole realistinen käytännön tilanteessa? 3 p.
Ääniaaltojen energiaa absorboituu ilmaan ja tiellä oleviin esteisiin. Näin ollen ääni vaimenee tehokkaammin kuin edellä kuvatussa ideaalitilanteessa. Etäisyys, jossa intensiteettitaso on vaimentunut 30 desibeliin, on siis käytännössä huomattavasti pienempi kuin kohdassa 6.3 lasketussa ideaalitilanteessa.
Pisteytys:
On kerrottu ilmiöksi äänen absorptio ilmaan tai esteisiin (3 p.). Mikäli tämä puuttuu heijastuminen esteistä voi tuottaa 1 pisteen.
Tyypillisiä virheitä:
Perusteltu pelkällä etäisyydellä, vaimenemisella tai hälyäänillä.
7. Käsikäyttöinen generaattori 15 p.
Aineiston kuvassa on esitetty käsikäyttöinen generaattori. Kun kestomagneetin sisällä oleva käämi pyörii tasaisella kulmanopeudella, syntyy kuvassa näkyvien mustan ja punaisen johtimen välille jaksollisesti vaihteleva jännite.
7.1 Selitä, miten jännite syntyy. 4 p.
Käämin pyöriessä sen läpäisevä magneettivuo muuttuu.
Käämiin syntyy induktiolain e = -N\frac{d\Phi}{dt} mukainen vaihtojännite.
Pisteytys:
On kerrottu, että magneettivuo käämin läpi muuttuu (2 p.) ja tämä muutos saa aikaan virran tai jännitteen (2 p.).
Tyypillisiä virheitä:
On väitetty, että magneettikenttä muuttuu.
7.2 Johda induktiolaista lähtien lauseke |e|=NBA\omega käämiin indusoituvan jännitteen huippuarvolle. Lausekkeessa N on käämin kierroslukumäärä, B kestomagneetin magneettivuon tiheys, A käämin pinta-ala ja \omega käämin kulmanopeus. 4 p.
Käämin läpäisevä magneettivuo \Phi = BA \cos\varphi = BA \cos(\omega t) , jossa \varphi on magneettikentän ja käämin välinen kulma ja \omega on käämin pyörimisen kulmanopeus.
e = -N\frac{d\Phi}{dt} = NAB \omega\sin(\omega t) = NAB\omega(\sin\varphi)\sin\varphi saa arvoja väliltä -1…+1, joten jännitteen maksimiarvoa vastaavassa tapauksessa |e|=NAB\omega.
Pisteytys:
Magneettivuon suureyhtälöä on derivoitu (2 p.).
Huippuarvo on perusteltu sini- tai cosini-funktion maksimiarvoilla (2 p.).
7.3 Simulaatio generaattorin tuottamasta jännitteestä on aineistossa . Voit säätää simulaatiossa pyörimisnopeutta, jolla isoa vetopyörää pyöritetään, ja lukea arvoja Ut-kuvaajasta, jossa U on käämin jännite. Neliön muotoisessa käämissä on 150 kierrosta ja käämin sivun pituus on 6 cm. Määritä simulaation avulla magneettivuon tiheys käämin kohdalla. 7 p.
Kohdan 7.2. yhtälöstä voidaan ratkaista lauseke magneettivuon tiheydelle: B=\frac{|e|}{NA\omega}=\frac{|e|}{Nr^2\frac{2\pi}{T}} , jossa T on vaihtojännitteen jaksonaika ja r käämin sivun pituus.
Esimerkkikuvassa maksimijännite on noin 7,5 V ja jaksonaika 0,42 s / 5 = 0,084 s. Sijoittamalla kuvaajasta luetut ja tehtävässä annetut arvot yhtälöön, saadaan magneettivuon tiheydeksi B=\frac{\rm 7,5 V}{150\cdot (\rm 0,06 m)^2\frac{2\pi}{0,084 s}}={\rm 0,1857}\,{\rm T}\approx{\rm 0,2}\,{\rm T}.
Pyörimisnopeus tulee säätää siten, että kuvaajasta on mahdollista lukea jännitteen ja jaksonajan arvot riittävällä tarkkuudella (n. 0,5...2,5 kierrosta sekunnissa).
Pisteytys:
On näytetty kuvaaja, josta on luettu kuvaajaan merkitty huippujännite (2 p.) ja jaksonaika (2 p.).
On ratkaistu suureyhtälö magneettivuon tiheydelle (1 p.).
On annettu 1-2 merkitsevän numeron tarkkuudella magneettivuon tiheys 0,18 T – 0,22 T (2 p.). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillisiä virheitä:
On käytetty simulaatioon syötettävää pyörimisnopeutta jaksonajan määrittämiseen sen sijaan, että luettaisiin se kuvasta.
8. Pieni Curie 15 p.
8.1 Artikkeli kuvaa ensimmäisessä maailmansodassa käytettyjä siirrettäviä röntgenkuvauslaitteita. Miksi röntgenlaitteita ei tuolloin voitu useinkaan kytkeä suoraan sähköverkkoon? 2 p.
Kaikissa kenttäsairaaloissa ei ollut sähköä. Lisäksi Ranskan sähköverkon jännite vaihteli ja se oli paikoin tasa- ja paikoin vaihtojännitettä.
Pisteytys:
On kerrottu, että sähköä ei ollut kaikkialla (1 p.).
On kerrottu, että jännitteen tyyppi tai suuruus vaihteli eri alueilla (1 p.).
Tyypillisiä virheitä:
Väitettiin, että jännitteen tyyppi ja suuruus vaihteli ajallisesti.
8.2 Säteily voitiin havaita kuvalevyllä tai fluoroskoopilla. Fluoroskoopissa oli lasilevy, joka oli päällystetty fluoresoivalla aineella, ja sen läpi voitiin katsoa potilaan röntgenkuvaa esimerkiksi kuvassa esitetyllä tavalla. Ensimmäisen maailmansodan aikana molempien menetelmien käyttö oli perusteltua. Kumpaa tapaa käyttäisit itse nykypäivänä ja miksi? 5 p.
Fluoroskoopilla lääkäri katsoi vammoja fluoresoivalta levyltä kuvauksen aikana. Se oli nopeampaa, ja siksi sitä suosittiin ensimmäisen maailmansodan aikana, mutta se aiheutti suuremman säteilyannoksen hoitohenkilökunnalle. Erityisen suurelle säteilyannokselle altistui, jos leikkasi potilasta röntgenkuvauksen aikana, kuten valokuvassa 8.B tapahtuu. Valokuvauslevylle kuvaaminen vaati pimiötä kuvan kehittämiseksi. Diagnostiikka oli siis hitaampaa. Etuna oli kuitenkin, että röntgenkuvasta jäi tallenne, johon voitiin palata myöhemmin.
Nykyään ionisoivan säteilyn haitat tunnetaan paremmin. Hoitohenkilökunnan ja potilaiden suojelemista säteilyltä painotettaisiin enemmän, ja siksi kuvalevyt olisivat näistä kahdesta vaihtoehdosta nykytiedon valossa parempi valinta.
Pisteytys:
On valittu kuvalevy (2 p.).
On kerrottu, että kuvalevyä käytettäessä röntgenlähteestä saatava säteilyannos on pienempi tai fluoroskopiaa käytettäessä suurempi (3 p.). Mikäli perustellaan pelkästään säteilylle altistumisella, perustelupisteitä ei anneta.
Tyypillisiä virheitä:
Perusteltiin valinta kuvantamisen hitaudella tai nopeudella.
Väitettiin, että säteilyä tulee jostain muualta kuin röntgenlähteestä.
8.3 Miksi aineistoissa kuvattuja vammoja tai keuhkosairauksia voidaan havaita röntgenkuvantamisella? Aineistossa on esimerkki influenssapotilaan röntgenkuvasta vuodelta 1918. 8 p.
Röntgenkuvan kontrasti syntyy eroista absorptiossa. Röntgensäteily on suhteellisen suurienergistä sähkömagneettista säteilyä. Röntgensäteily absorboituu aineeseen pääsääntöisesti irrottamalla elektronin atomista. Eri alkuaineilla on eri verran elektroneja. Siksi pehmytkudokset, jotka koostuvat pääosin pienen järjestysluvun alkuaineiden, kuten vedyn, hiilen ja hapen, muodostamista yhdisteistä, absorboivat vähemmän röntgensäteilyä kuin paljon kalsiumia sisältävä luukudos tai metalliset vierasesineet. Röntgenkuvantamisella voi siis havaita parhaiten luunmurtumia tai esimerkiksi sirpaleita. Pehmytkudosten vammoja sillä on vaikeampi nähdä. Toisaalta röntgensäteilyä absorboituu hyvin vähän kaasuun, koska kaasun tiheys on pienempi kuin pehmytkudosten. Röntgenkuvauksella voi siis myös nähdä, jos keuhkoihin on kertynyt kaasun tilalle nestettä.
Pisteytys:
On selitetty, että havaitaan eroja kehon läpi kulkeneessa säteilyssä (2 p.). Jos väitetään, että röntgensäteet heijastuvat potilaan sisällä, näitä pisteitä ei anneta.
On selitetty alkuaineiden järjestysluvun vaikuttavan siihen, miten aine absorboi tai vaimentaa säteilyä (2 p.).
On selitetty aineiden tiheyden vaikuttavan siihen, miten aine absorboi tai vaimentaa säteilyä (2 p.).
On mainittu yksi kontrastia aiheuttava pari (esimerkiksi pehmytkudos ja luut) ja selitetty niiden erottuvan erilaisen absorption perusteella (2 p.).
Tyypillisiä virheitä:
Vastattiin kysymykseen mitä röntgenkuvantamisella voidaan nähdä. Selitettiin näytettyjä röntgenkuvia.
Osa 3: 20 pisteen tehtävät
9. Gammasäteilyn ja aineen välinen vuorovaikutus 20 p.
Gammafotoni eli korkeaenergiainen fotoni vuorovaikuttaa aineen kanssa kolmella eri tavalla. Kuvassa on esitetty todennäköisin fotonin vuorovaikutustapa eri energioilla ja alkuaineen järjestysluvuilla.
9.1 Mitä fotonille tapahtuu, ja mihin sen energia siirtyy valosähköilmiössä ja parinmuodostuksessa? 6 p.
Valosähköilmiössä fotoni katoaa ja lähes koko sen energia siirtyy väliaineen elektronille.
Parinmuodostuksessa fotoni katoaa synnyttäen (tavallisimmin) elektronin ja positronin, jotka saavat fotonin energian massana ja kineettisenä energiana. Osa fotonin energiasta (1 022 keV) muuttuu elektronin ja positronin massaksi.
Pisteytys:
On mainittu, että valosähköilmiössä fotoni katoaa (1 p.) ja sen energia siirtyy elektronille (2 p.).
On mainittu, että parinmuodostuksessa fotoni katoaa tai muuttuu aineeksi (1 p.) ja sen energia siirtyy hiukkas-antihiukkasparille (2 p.).
9.2 Comptonin ilmiössä fotoni siroaa elektronista. Sironneen fotonin energia on E^\ast=\frac{E}{1+\frac{E}{m_ec^2}(1-\cos\theta)} jossa E on alkuperäisen fotonin energia, \theta on siroamiskulma ja m_e on elektronin massa. Mikä on suurin liike-energia, jonka elektroni voi saada fotonilta, kun 662 keV:n fotoni siroaa siitä? 6 p.
Kokonaisenergian säilymisen perusteella elektronin saama kineettinen energia on yhtä suuri kuin fotonin energian muutos, eli E_e=E-E^\ast.
Fotonin energianmuutos on suurin, kun \theta on 180°, koska tällöin E^\ast saa pienimmän arvonsa. Saadaan
E_e=E-E^\ast = E-\frac{E}{1+\frac{2E}{m_ec^2}}=E\biggl(1-\frac{1}{1+\frac{2E}{m_ec^2}}\biggr)={\rm 662}\,{\rm keV}\biggl(1-\frac{1}{1+\frac{2\cdot {\rm 662}\,{\rm keV}}{{\rm 511}\,{\rm keV}}}\biggr)={\rm 477,65}\,{\rm keV}\approx {\rm 478}\,{\rm keV}.
Pisteytys:
On kirjoitettu oikea suureyhtälö elektronin energialle fotonien energioiden avulla (2 p.).
On todettu, milloin fotonin energia on pienimmillään, tai laskettu fotonin pienimmän energian arvo (2 p.).
On annettu 3 merkitsevän numeron tarkkuudella elektronin energia (2 p.). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillisiä virheitä:
Ajateltiin fotonin energian olevan pienimmillään kulman ollessa 90˚.
Ajateltiin sironneen fotonin energian olevan 662 keV. Tällaista Compton-sirontaa ei voi olla, sillä sironneen fotonin energia voi olla korkeintaan puolet elektronin lepoenergiasta. Jos annetusta yhtälöstä yrittää ratkaista alkuperäisen fotonin energiaa sille saa imaginäärisen ratkaisun.
9.3
Kahdella erilaisella tilavuudeltaan pienellä ilmaisimella havaittiin Cs-137-säteilylähteen tuottamaa 662 keV:n gammasäteilyä. Toinen ilmaisimista on tehty muovista, ja toinen taas sisältää vismuttia, germaniumia ja happea. Ilmaisimilla saadut energiaspektrit on esitetty kuvassa , jossa N on havaittujen tapahtumien lukumäärä eri energioilla.
Molemmat ilmaisimet ovat niin sanottuja tuikeilmaisimia, joissa nopeasti liikkuvan varatun hiukkasen aiheuttama ionisaatio synnyttää näkyvää valoa. Syntyneen valon määrä on verrannollinen ionisoivan hiukkasen liike-energiaan. Ilmaisimet eivät siis suoraan havaitse gammasäteilyä vaan säteilyn välillisesti aiheuttaman ionisaation.
Selitä, mitä on todennäköisimmin tapahtunut ilmaisimissa, kun spektreihin on ilmaantunut tapahtumia alle 400 keV:n alueelle. Mitä on todennäköisimmin tapahtunut kuvan spektrin A ilmaisimessa, kun spektriin on ilmaantunut tapahtuma noin kohtaan 660 keV? Kumpi kuvan spektreistä (A/B) on muovista valmistetun ilmaisimen spektri? Voit olettaa, että gammafotoni vuorovaikuttaa ilmaisimessa vain kerran.
8 p.
Koska gammafotonien energia on alle 1 022 keV, parinmuodostusta ei voi tapahtua. Kaikissa tapauksissa osa fotonin energiasta tai kaikki sen energia siirtyy elektronille. Elektroni ionisoi ilmaisimien ainetta, mistä syntyy havaittava valo.
Mikäli gammafotoni Compton-siroaa ilmaisimesta, elektronille jää edellisen tehtävän perusteella alle 500 keV energiaa (elektroni absorboituu ilmaisimeen). Mikäli sirontakulma on pienempi, elektronille jää vielä vähemmän energiaa. Tapahtumat alle 400 keV syntyvät, kun fotoni kokee Comptonin sironnan ilmaisimen kanssa.
Jos fotoni kokee valosähköilmiön, sen koko energia saadaan havaittua elektronin absorboituessa ilmaisimeen. Tämä vastaa spektrin piikkiä, jonka energia on yhtä suuri kuin fotonin energia.
Spektri B on muovisen ilmaisimen tuottama. Muovi koostuu lähinnä hiilestä ja vedystä, joiden järjestysluku on pieni. Kuvan 9.A perusteella 662 keV:n gammafotoni vuorovaikuttaa lähinnä Comptonin sironnalla ilmaisimessa, jolloin havaitaan tapahtumia vain alle 500 keV:n energioilla. Vismutti-germanium-happi-ilmaisimen keskimääräinen järjestyluku on suurempi, joten sillä on nähtävissä myös valosähköisen ilmiön aiheuttama kokonaisabsorptio 660 keV:n kohdalla.
Pisteytys:
On liitetty ilmaisimessa B alle 400 keV:n kohdalla näkyvä signaali Compton-sirontaan (2 p.).
On liitetty ilmaisimessa A näkyvä 662 keV:n kohdalla näkyvä signaali valosähköilmiöön (2 p.).
On valittu muovi-ilmaisimeksi B (2 p.) ja perusteltu valinta vertailemalla alkuaineiden järjestyslukuja muovissa ja BiGeO-ilmaisimessa ja kytketty ne Compton-sironnan ja valosähköilmiön todennäköisyyteen (2 p.).
10. Parafiinin sulamislämpö 20 p.
Haluat kokeellisesti määrittää materiaalin ominaissulamislämmön fysiikan oppitunnilla. Tehtävänä on suunnitella mahdollisimman yksinkertainen mittausjärjestely sekä siihen liittyvä tulosten käsittely.
Olet valinnut materiaaliksi parafiinin, jonka sulamispiste on 60 °C. Yksinkertaiseen koejärjestelyyn sinulla on käytettävissä seuraavat tarvikkeet:
- solupolystyreeniastia (eli styrox-astia)
- vettä vesihanasta ja vedenkeitin, jonka tehoa ei tunneta
- kiinteätä parafiinia huoneenlämpötilassa 20 °C
- sakset, pinsetti, teippiä, muovipusseja, alumiinifoliota
- suppea taulukkokirja, josta saat veden ominaisuudet riittävällä tarkkuudella mutta et saa parafiinin tietoja.
Yllä mainittujen tarvikkeiden lisäksi fysiikan luokassa on saatavilla vain seuraavat välineet:
- kello
- työntömitta
- lämpömittari
- mittalasi
- vaaka
- ominaispainomittari
- kosteusmittari
- ohutseinäinen alumiiniastia.
10.1
Mitkä ovat työn päävaiheet ja niissä tehtävät mittaukset? Miten määrität mittaustuloksista parafiinin ominaissulamislämmön?
Esitä tarvittavat suureyhtälöt. Jos tarvitset graafista esitystä tuloksen määrittämiseen, hahmottele sellainen olettamistasi mittaustuloksista. Halutessasi voit käyttää apuna aineiston piirrospohjaa.
Mitkä numeroidun listan välineistä tarvitset tässä työssä? Anna niistä luettelo.
14 p.
Oleellista on mitata kuuman veden parafiinille antama lämpömäärä sulamisen aikana. Ennen kuin parafiini voidaan sulattaa, se täytyy lämmittää sulamispisteeseensä.
Kuumennetaan vedenkeittimellä vettä kiehumispisteeseen.
Punnitaan parafiinipala (massa m_{\rm p}) ja viedään se styrox-astiaan. (Parafiinipala voi olla ohutseinäisessä alumiiniastiassa tai alumiinifoliossa, joka asetetaan styrox-astiaan, ja kuuma vesi voidaan kaataa sen viereen. Koska parafiini ei missään vaiheessa sekoitu veteen, tämä ei ole välttämätöntä, mutta vähentää sotkua.) Otetaan keittimestä (mahdollisesti mittalasilla) pieni määrä kuumaa vettä. Mitataan veden massa ja alkulämpötila T0 ja kaadetaan vesi styrox-astiaan. Odotetaan hetki, että lämpötila tasaantuu, ja mitataan se. Näin mitattu lämpötila kuvaa sekä veden että parafiinin lämpötilaa.
Lisätään pieni määrä kuumaa vettä, jonka massa mitataan ja jonka alkulämpötilaksi pyritään saamaan T0. Annetaan systeemin lämpötilan tasaantua ja mitataan se. Toistetaan veden lisäämistä ja mitataan samat suureet. Styrox-astiassa olevan veden lämpötila nousee joka kerralla, mikä vastaa parafiinipalan lämpenemistä. Jossain vaiheessa saavutetaan sulamispiste 60 ˚C. Tästä alkaa mittauksen hyödynnettävä osuus, jonka aikana systeemin loppulämpötila ei veden lisäämisestä huolimatta nouse.
Jatketaan kuuman veden lisäämistä vaiheittain, kunnes havaitaan loppulämpötilan jälleen alkavan kasvaa. Tässä vaiheessa kaikki parafiini on sulanut ja mittaus voidaan lopettaa.
Mittaustuloksina saadaan loppulämpötila T veden massan m funktiona. Piirretään (m,T)-käyrä, josta tulee oheisen kuvan kaltainen. Graafisen esityksen perusteella saadaan selville, mistä veden massasta M_a alkaen lämpötila pysyy vakiona ja mistä määrästä M_l alkaen sen lämpötila alkaa jälleen nousta. Näiden massojen erotuksen \Delta M = M_l – M_a avulla saadaan selville vedestä parafiiniin siirtyvä lämpömäärä Q=c\Delta M\Delta T, missä c on veden ominaislämpökapasitetti. Lämpötilaero \Delta T=T_0-{\rm 60}\,^{\rm o}{\rm C}.
Tämä lämpö käytetään parafiinin sulattamiseen, eli Q=sm_p.
Tästä saadaan parafiinin sulamislämpö s=c\Delta M\Delta T/m_p.
Numeroiduista välineistä mittauksessa tarvitaan vaakaa veden massan ja parafiinin massan mittaamiseen ja lämpömittaria veden lämpötilan mittaamiseen. Mittauksessa voidaan käyttää kelloa, mittalasia ja ohutseinäistä alumiiniastiaa sekä numeroimattomia tarvikkeita.
Ratkaisuna voi esittää myös muita tapoja. Yllä esitetyn menetelmän variaationa koko vesimäärä voidaan lisätä kerralla, jos koe sitten toistetaan eri vesimäärillä riittävän monta kertaa. Parafiinin voi myös sulattaa vedenkeittimellä siten, että keittimessä on vettä, parafiini on alumiiniastiassa keittimen sisällä. Tällöin tulee kuvata myös menetelmä vedenkeittimen tehon määrittämiseen.
Ratkaisut arvosteltiin luokittelemalla ne neljään ryhmään:
A. Sulamislämmön määrittäminen onnistuu hyvin.
B. Sulamislämmön määrittäminen saattaa onnistua, mutta tapa on epätarkka tai epäkäytännöllinen. Pisteitä voi saada välineistä ja suureyhtälöistä.
C. Määritetään sulamislämpöä tavalla, joka ei voi antaa oikeaa vastausta. Pisteitä voi saada välineistä ja korkeintaan yhdestä suureyhtälöstä.
D. Ei määritetä mitään tai määritetään jokin muu suure kuin sulamislämpö. Pisteitä voi saada vain välineistä.
Pisteytys:
On mainittu numeroidusta listasta vaaka (2 p.) ja lämpömittari (2 p.). Jos on väitetty tarvittavan työntömittaa, ominaispainomittaria tai kosteusmittaria, vähennetään kustakin yksi piste.
On selitetty, miten suureyhtälöitä Q_v=c_v\Delta M_v\Delta T_v ja Q_s=s_p m_p käytetään ominaislämmön määrittämisessä (2 p.) + (2 p.). Yhtälöiden lisäksi edellytetään käytettyjen suureiden määrittelyä ja kuvausta suureiden mittaamisesta.
On annettu suureyhtälö parafiinin ominaislämmölle mitattujen suureiden avulla (2 p.).
On kuvattu hyvä menetelmä parafiinin ominaislämmön mittaamiselle (4 p.). Hyvään menetelmään kuuluu esimerkiksi lämpötilan mittaaminen termisessä tasapainossa.
Tyypillisiä virheitä:
Määritetään sulamispiste, ei sulamislämpö (tyyppi D).
Ei oteta huomioon, että parafiini täytyy lämmittää ensin sulamispisteeseen tai lämmitetään parafiinia nestemäisenä (tyyppi C).
Sulatetaan parafiinia vedellä, jonka lämpötila on 60˚C (tyyppi C).
Lisätään styrox-astiaan kerralla suuri määrä vettä, ja mitataan veden lämpötilaa sen koko ajan muuttuessa. Käytetään veden lämpötilaa sulamisen alkaessa ja päättyessä (tyyppi B).
10.2 Vertaat lopuksi mittauksista saamaasi sulamislämmön arvoa kirjallisuusarvoon. Luettele kolme tärkeätä tekijää, jotka aiheuttavat mittaamaasi arvoon poikkeaman kirjallisuusarvosta. 6 p.
Esimerkkejä oikeista poikkeamista
- virhe tai epätarkkuus massan punnituksissa
- kuuman veden lämpötilan vaihtelu
- lämpöhäviöt sulatusprosessin aikana
- epämääräisyys sulamisen alkamisessa ja loppumisessa (veden lisääminen portaittain)
Pisteytys:
On mainittu lämpöhäviöt jossain prosessin vaiheessa (2 p.).
On mainittu epämääräisyys sulamisen alkamisen tai päättymisen havaitsemisessa tai termisessä tasapainossa (2 p.).
On mainittu virhe yhdessä nimetyssä mittauksessa tai mittalaitteessa (2 p.).
Tyypillisiä virheitä:
Väitetään virheen lähteeksi alumiiniastian lämpökapasiteettia, laboratorion lämpötilan tai ilmanpaineen vaihtelua, systemaattista virhettä, laskuvirhettä, toistomittauksen puutetta, epäpuhtauksia tai epämääräistä mittausvirhettä.
11. James Webb -avaruusteleskooppi 20 p.
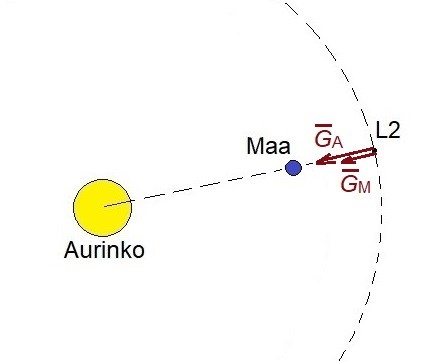
Joulupäivänä 2021 Ranskan Guayanasta laukaistiin Ariane 5 -kantoraketti, joka lähetti James Webb -avaruusteleskoopin (kuva ) Aurinko-maa-järjestelmän Lagrangen pisteeseen L2. Tähän pisteeseen sijoitettu teleskooppi kiertää Aurinkoa pysyen likimain Auringon ja Maan kautta kulkevalla suoralla (kuva ). Teleskooppi liikkuu vakioetäisyydellä Maasta siten, että Aurinko ja Maa ovat siitä katsoen koko ajan samalla puolella. James Webb -avaruusteleskooppi toimii lähinnä infrapuna-alueella. Sen avulla tutkitaan muun muassa maailmankaikkeuden kaukaisimpia kohteita ja toisten aurinkokuntien planeettoja.
11.1 James Webb -teleskooppi sijoitettiin avaruuteen, jossa sen lämpötila saatiin alhaiseksi. Miksi alhainen lämpötila on olennainen tekijä infrapunasäteilyn havainnoinnissa? 3 p.
Infrapunasäteilyä havainnoitaessa teleskoopin itsensä tuottama infrapunasäteily saattaisi häiritä mittauksia ja on siksi eliminoitava niin perusteellisesti kuin mahdollista. Tämä toteutetaan pitämällä havaintolaitteet erittäin alhaisessa lämpötilassa.
Pisteytys:
On mainittu syyksi teleskoopin oma lämpösäteily (3 p.).
Tyypillisiä virheitä:
Vastataan, että teleskoopin lämpötilan tulee olla alhainen.
Mainitaan syyksi ympäristön lähettämä lämpösäteily.
11.2 Miksi kuvassa näkyvä teleskoopin lämpösuoja ei ole yhtenäinen kerros, vaan koostuu viidestä erillään olevasta kerroksesta? 4 p.
Jos lämpösuoja olisi yhtenäinen kerros, lämpö pääsisi siirtymään johtumalla sen läpi. Lämpösuojan kerrosten väleissä olevassa tyhjiössä lämmön johtuminen ei ole mahdollista.
Pisteytys:
On mainittu lämmön johtuminen kerroksessa (2 p.).
On mainittu, että levyjen välinen tyhjiö ei johda lämpöä tai että lämpö johtuu kerrosten välissä vain säteilemällä (2 p.).
Pohdinta rakenteen painosta ei tuota pisteitä eikä pistevähennyksiä.
Tyypillisiä virheitä:
Väitetään, että levyjen välissä oleva ilma ei johda lämpöä.
Väitetään, että viisi kerrosta eristää paremmin kuin yksi.
Vastataan kysymykseen, miksi teleskoopilla on lämpösuoja.
11.3 Piirrä teleskoopin voimakuvio ja nimeä voimat. 4 p.
Voimakuviossa \bar{G}_{\rm A} ja \bar{G}_{\rm M} ovat Auringon ja Maan avaruusteleskooppiin kohdistamat gravitaatiovoimat. Auringon avaruusteleskooppiin kohdistaman gravitaatiovoiman suunta on kohti Aurinkoa ja Maan kohdistaman voiman suunta kohti Maata. Voimat ovat lähes yhdensuuntaiset. Tarkempi analyysi osoittaa, että kuvattu ympyrärata on epästabiili, joten käytännössä teleskooppi liikkuu L2:n ympäristössä ja ratakorjaukset ovat välttämättömiä. Tätä ei ratkaisussa oteta huomioon.
Pisteytys:
Voimakuviossa on esitetty satelliitti ja siihen vaikuttavat kaksi voimaa. Voimat on nimettävä Auringon ja Maan gravitaatiovoimiksi ja niiden symbolien (skalaari tai vektori) on näyttävä kuvassa. Voimien suunta tulee olla joko kohti kuvassa näkyvää Aurinkoa ja Maata tai kohtisuorassa ympyrän kaarella kuvatun radan tangenttia vastaan. (4 p.).
Jos jonkin voiman suunta on väärä tai ei käy ilmi tai voiman suuresymboli puuttuu, pisteitä ei anneta. Jos kuviossa on Aurinkoon tai Maahan kohdistuvia voimia, muita ylimääräisiä voimia tai nopeus- tai kiihtyvyysvektori on kiinni satelliitissa, pisteitä ei anneta.
Jos voimien nimeäminen gravitaatiovoimiksi puuttuu, vähennetään yksi piste.
Tyypillisiä virheitä:
Kuvasta ei käy ilmi, missä Maa ja Aurinko ovat, eli voimien suunta ei ole määritetty.
Voimakuvioon on merkitty Maahan ja aurinkoon vaikuttavia voimia.
11.4 Teleskoopin etäisyys Maasta on 1,5 miljoonaa kilometriä. Perustele tämä osoittamalla, että Newtonin II laki toteutuu kyseisellä etäisyyden arvolla. 9 p.
Gravitaatiovakio, Auringon massa, Maan massa, Auringon ja Maan välinen etäisyys sekä Maan ja avaruusteleskoopin kiertoaika Auringon ympäri ovat
\gamma={\rm 6,674}\cdot{\rm 10}^{\rm -11}\,\frac{{\rm Nm}^2}{{\rm kg}^2} m_{\rm A}={\rm 1,989}\cdot{\rm 10}^{\rm 30}\,{\rm kg}, m_{\rm M}={\rm 5,974}\cdot{\rm 10}^{\rm 24}\,{\rm kg} r={\rm 1,4960}\cdot{\rm 10}^{\rm 8}\,{\rm km}, T={\rm 365,2}\,{\rm d}Newtonin II laki Lagrangen pisteeseen L2 sijoitetulle avaruusteleskoopille on ma=G_{\rm A}+G_{\rm M} , jossa m on teleskoopin massa, a teleskoopin normaalikiihtyvyys ja G_{\rm A} ja G_{\rm M} Auringon ja Maan teleskooppiin kohdistamat gravitaatiovoimat. Sijoitetaan tähän a=\frac{v^2}{r+d}=\frac{[2\pi(r+d)/T)]^2}{r+d}=\Bigl(\frac{2\pi}{T}\Bigr)^2(r+d) jossa v on teleskoopin nopeus ja d L2:n etäisyys Maasta, ja G_{\rm A}=\gamma\frac{m_{\rm A}m}{(r+d)^2}, G_{\rm M}=\gamma\frac{m_{\rm M}m}{d^2}, ja supistetaan pois teleskoopin massa. Näin saadaan \Bigl(\frac{2\pi}{T}\Bigr)^2(r+d)=\gamma\Bigl(\frac{m_{\rm A}}{(r+d)^2}+\frac{m_{\rm M}}{d^2}\Bigr)
Osoitetaan, että tämä toteutuu kun d = 1,5 ∙ 106 km. Sijoittamalla suureiden arvot saadaan yhtälön vasemman puolen arvoksi 5,9915\cdot 10^{-3}\,\text{m/s}^2 ja oikean puolen arvoksi 5,9914\cdot 10^{-3}\,\text{m/s}^2. Nämä ovat riittävän tarkasti yhtä suuret, joten annettu d:n arvo toteuttaa Newtonin II lain.
Pisteytys:
On esitetty Newtonin II lain mukainen suureyhtälö ma=G_{\rm A}+G_{\rm M} satelliittiin vaikuttaville voimille (2 p.).
On esitetty satelliitin normaalikiihtyvyydelle suureyhtälö, jossa käytetyn radan säteen on kerrottu olevan satelliitin etäisyys Auringosta (2 p.) Auringon ja Maan säteen saa lisätä etäisyyksiin, sillä niiden tuottama virhe on marginaalisen pieni.
On ratkaistu teleskoopin ratanopeus sen kiertäessä Auringon kerran vuodessa tai kulmanopeus sen kiertäessä Aurinkoa samalla kulmanopeudella Maan kanssa (2 p.).
Edellyttäen, että kaikki edellä esitetyt asiat ovat oikein, todetaan tunnetut suurearvot sijoittamalla yhtälön oikean puolen ja vasemman puolen kiihtyvyyden olevan yhtä suuri (2 p.) ja Newtonin II lain olevan voimassa (1 p.).
Tyypillisiä virheitä:
Unohdetaan joko Maan tai Auringon aiheuttama gravitaatio. Kierretään Maata Auringon sijaan.