Beskrivningar av goda svar: SV – Fysik
24.3.2023
Slutgiltiga beskrivningar av goda svar 16.5.2023
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
Del 1: 20-poängsuppgift
1. Ifyllnadsuppgifter från fysikens olika delområden 20 p.
Nedan finns 10 ifyllnadsuppgifter (1.1–1.10). Välj det alternativ som passar bäst för varje situation. Rätt svar ger 2 p., fel svar 0 p. och inget svar 0 p.
1.1 Komplettera meningen. 2 p.
- lika med (2 p.)
1.2 Komplettera meningen. 2 p.
- accelererad rörelse (2 p.)
1.3 Komplettera meningen. 2 p.
- rörelsemängd (2 p.)
1.4 Komplettera meningen. 2 p.
- en skalärstorhet (2 p.)
1.5 Komplettera meningen. 2 p.
- stiga (2 p.)
1.6 Komplettera meningen. 2 p.
- ha samma förtecken (2 p.)
1.7 Komplettera meningen. 2 p.
- longitudinell (2 p.)
1.8 Komplettera meningen. 2 p.
- växelspänningens storlek (2 p.)
1.9 Komplettera meningen. 2 p.
- \alpha (2 p.)
Mängden jonisering som sker i en tunn metallfolie beror på tre faktorer: strålningens typ, strålningens intensitet och strålningens energi. Av de här faktorerna är intensitet och energi reglerbara storheter, och genom att välja intensiteten eller energin stor för en av strålningstyperna och liten för de andra kan man få den högsta dosen av den utvalda strålningstypen. Eftersom det här kan göras för alla strålningstyper måste man kunna förbise effekten av intensiteten och energin och i stället betrakta den typiska joniseringsförmågan hos strålningen när man söker rätt svar.
1.10 Komplettera meningen. 2 p.
- det infraröda området (2 p.)
Del 2: 15-poängsuppgifter
2. Bärraketen Ariane 5 15 p.
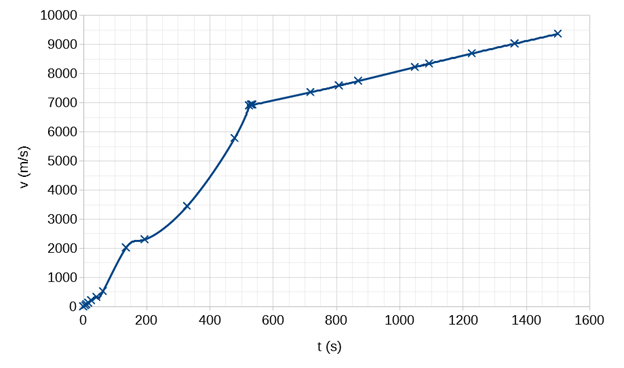
2.1 Gör en grafisk presentation av raketens fart som funktion av tiden. Framställ presentationen så att den visar mätpunkterna i materialet och så att raketens fart vid vilken tidpunkt som helst inom intervallet 0 s–1 500 s kan avläsas från den. 5 p.
Poängsättning:
Det har presenterats en graf där de uppmätta värdena för farten som funktion av tiden syns som enskilda mätpunkter. I presentationen ska det synas en enhetlig kurva mellan mätpunkterna från vilken farten vid vilken som helst tidpunkt kan avläsas. En enhetlig kurva kan bäst fås med en spline-interpolation men för det här materialet fungerar också en bruten linje mellan mätpunkterna bra. (5 p.) Om kurvan saknas eller är olämplig för punkterna är avdraget 2 poäng. Om mätpunkterna inte markerats som enskilda punkter är avdraget 2 poäng.
Om storhetens beteckning eller enhet saknas eller axlarna är fel väg är avdraget för varje fel 1 poäng.
Typiska fel:
Det har ritats en till mätpunkterna anpassad funktion som inte går genom mätpunkterna.
2.2 Hur lång sträcka färdades raketen längs sin bana under tidsintervallet 0 s–1 500 s? 5 p.
Poängsättning:
Ur svaret framgår det att grafisk integrering har använts för att bestämma sträckan. (2 p.)
Svaret har givits med 2-3 gällande siffrors noggrannhet som en sträcka inom intervallet 9400 km – 9800 km. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiskt fel:
Sträckan som färdats har beräknats ur storhetsekvationen s = vt med någon hastighet och tid.
2.3 Hur stor var raketens acceleration längs banan under tidsintervallet 700 s – 1 400 s? 5 p.
Poängsättning:
I lösningen har det berättats att raketen är i likformigt accelererad rörelse under det undersökta tidsintervallet. Alternativt har en rät linje, anpassad till intervallet 700 s – 1400 s, och vars riktningskoefficient har använts, presenterats i lösningen. (2 p.)
Som svar har givits med 2-3 gällande siffrors noggrannhet en acceleration inom intervallet
2,4 m/s2 – 2,8 m/s2. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiskt fel:
Momentan eller medelacceleration har använts.
3. Värmeöverföringsmaskiner 15 p.
Välj det alternativ som förklarar situationen bäst på ett fysikaliskt sätt i deluppgifterna 3.1–3.8 gällande värmeöverföringsmaskiner.
Flervalsuppgiften är inte obligatorisk, alltså behöver du inte besvara den. Du kan ändra ditt svar efter att du har valt ett svarsalternativ, men du kan inte längre lämna deluppgiften helt utan svar. Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning, ska du välja alternativet ”Jag svarar inte” för alla deluppgifter.
I deluppgifterna 3.1–3.3 undersöker vi en luftvärmepump, med vars hjälp energi överförs från kallare utomhusluft till varmare inomhusluft i en byggnad. Anordningen har en inomhusenhet och en utomhusenhet mellan vilka ett värmeöverförande ämne cirkulerar.
3.1 Varför är det möjligt för energi att överföras från den kalla utomhusluften till det värmeöverförande ämnet i utomhusenheten? 1 p.
- Ämnet är kallare än utomhusluften. (1 p.)
3.2 Vad händer med det värmeöverförande ämnet när det är i förångaren? 2 p.
- Ämnet förångas och tar emot energi från omgivningen. (2 p.)
3.3 Värmepumpens elektriska effekt är 1 000 W. Rätt storleksordning för värmepumpens uppvärmningseffekt är 2 p.
- 3 000 W (2 p.)
3.4 Ett kylskåp behöver elektrisk energi för att fungera. Vad händer med kylskåpets elförbrukning om det sker en bestående höjning av rumstemperaturen? 2 p.
- Elförbrukningen ökar. (2 p.)
3.5 Dörren till ett påslaget kylskåp lämnas öppen för en längre tid. Vad händer med rumstemperaturen? 2 p.
- Temperaturen stiger. (2 p.)
3.6 Vilket av följande diagram föreställer funktionsprincipen för en värmeöverföringsmaskin? Diagrammets pilar visar riktningen i vilken energi överförs, och den gula lådan föreställer själva maskinen. 2 p.
 (2 p.)
(2 p.)
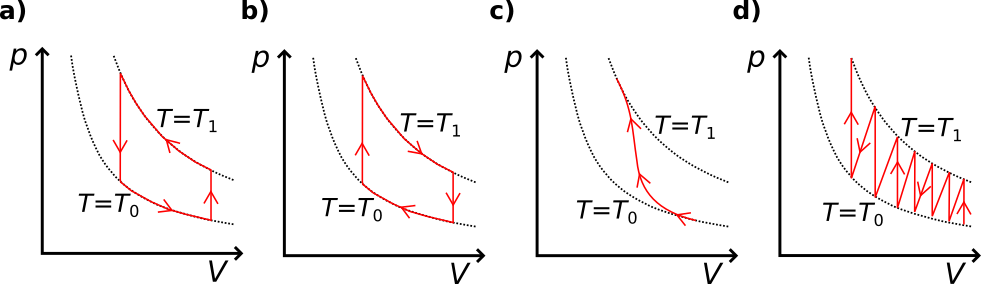
3.7 Vilken av följande grafer föreställer funktionen för en ideal värmeöverföringsmaskin? I den här situationen förblir ämnet i gasform. 2 p.
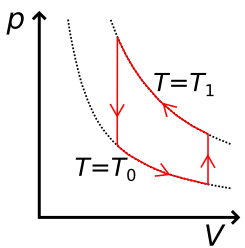 (2 p.)
(2 p.)
3.8 I ett visst arbetsskede i en ideal värmeöverföringsmaskin utförs ett arbete på ämnet, men ingen energi överförs mellan ämnet och omgivningen. Ämnet förblir i gasform under hela arbetsskedet. Vad händer med gasens temperatur och volym? 2 p.
- Gasens temperatur stiger och dess volym minskar. (2 p.)
- Gasens temperatur förblir konstant och dess volym minskar. (2 p.)
På grund av ett fel i det svenskspråkiga provet godkänns även svaret ”Gasens temperatur förblir konstant och dess volym minskar.” i det svenskspråkiga provet.
4. En kondensator 15 p.
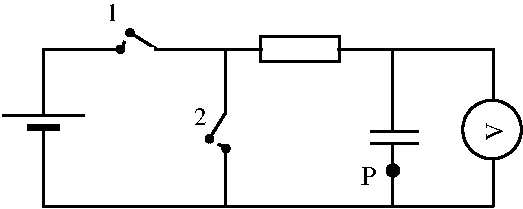
4.1 Bild visar spänningen mellan kondensatorplattorna som funktion av tiden. Komplettera det halvfärdiga kopplingsschemat i bild så att den färdiga kretsen skulle kunna producera en liknande graf som i bild . Använd två strömbrytare, ledningar, ett motstånd och en spänningsmätare. Du kan använda dig av bilderna av komponenter , och . Förklara hur mätningen utförs med ditt kompletterade kopplingsschema och i vilken ordning strömbrytarna ska slutas eller brytas. 8 p.
Ur bild 4.A märker vi att kondensatorns spänning ändrar exponentiellt och inte plötsligt. Det här orsakas av motståndet som är kopplat i serie med kondensatorn. Eftersom det tar lika länge att ladda upp kondensatorn som att ladda ur den så måste motståndet vara samma i båda situationerna. Utgående från det här bygger vi kretsen nedanför där positionerna för motståndet, strömbrytarna och spänningsmätaren syns.
Strömbrytare 1 sluts när kondensatorn ska laddas upp. Sedan öppnas strömbrytare 1 och strömbrytare 2 sluts, varvid kondensatorn laddas ur. Potentialskillnaderna över kondensatorn kan mätas med spänningsmätaren.
Poängsättning:
Komponenterna är kopplade så att det är möjligt för en kondensator att en laddas upp (2 p) och laddas ur (2 p) i enlighet med bild 4.A genom att sluta eller öppna strömbrytare.
Användningen av strömbrytarna är beskriven på ett sådant sätt att en uppladdning (2 p) och urladdning (2 p) sker i enlighet med bild 4.A.
Om spänningsmätaren är kopplad så att den mäter något annat än spänningen över kondensatorn ges inga poäng för deluppgiften,
Typiskt fel:
Motståndet har kopplats i serie med strömbrytare 2, med påföljden att kondensatorn laddas upp med en mycket mindre tidskonstant än vid urladdningen. En sådan lösning ger högst 4 poäng.
4.2 Är strömmens riktning uppåt eller neråt i punkten P i bild vid tidpunkterna t1 och t2 i uppladdningsgrafen? 4 p.
Vid tidpunkten t1 laddas kondensatorn upp och strömmens riktning är då neråt i bilden. Vid tidpunkten t2 laddas kondensatorn ur och strömmens riktning är uppåt.
Poängsättning:
Rätt riktning från de givna alternativen är kopplade till rätt tidpunkter t1 (2 p) och t2 (2 p).
4.3 Hur skulle du ändra kretsens komponenter om du vill göra kondensatorns upp- och urladdning långsammare? 3 p.
Upp- och urladdningshastigheten kan minskas genom att man använder ett motstånd med större resistans eller en kondensator med större kapacitans. Toppvärdet för spänningen bestäms fortsättningsvis av spänningskällans polspänning i en öppen krets.
Poängsättning:
Antingen ökande av kapacitansen, ökande av resistansen eller kopplande av ett till motstånd i serie har omnämnts. (3 p.)
Typiskt fel:
Det har omnämnts att ett till motstånd används utan att förklara hur det kopplas.
5. Ett stearinljus 15 p.
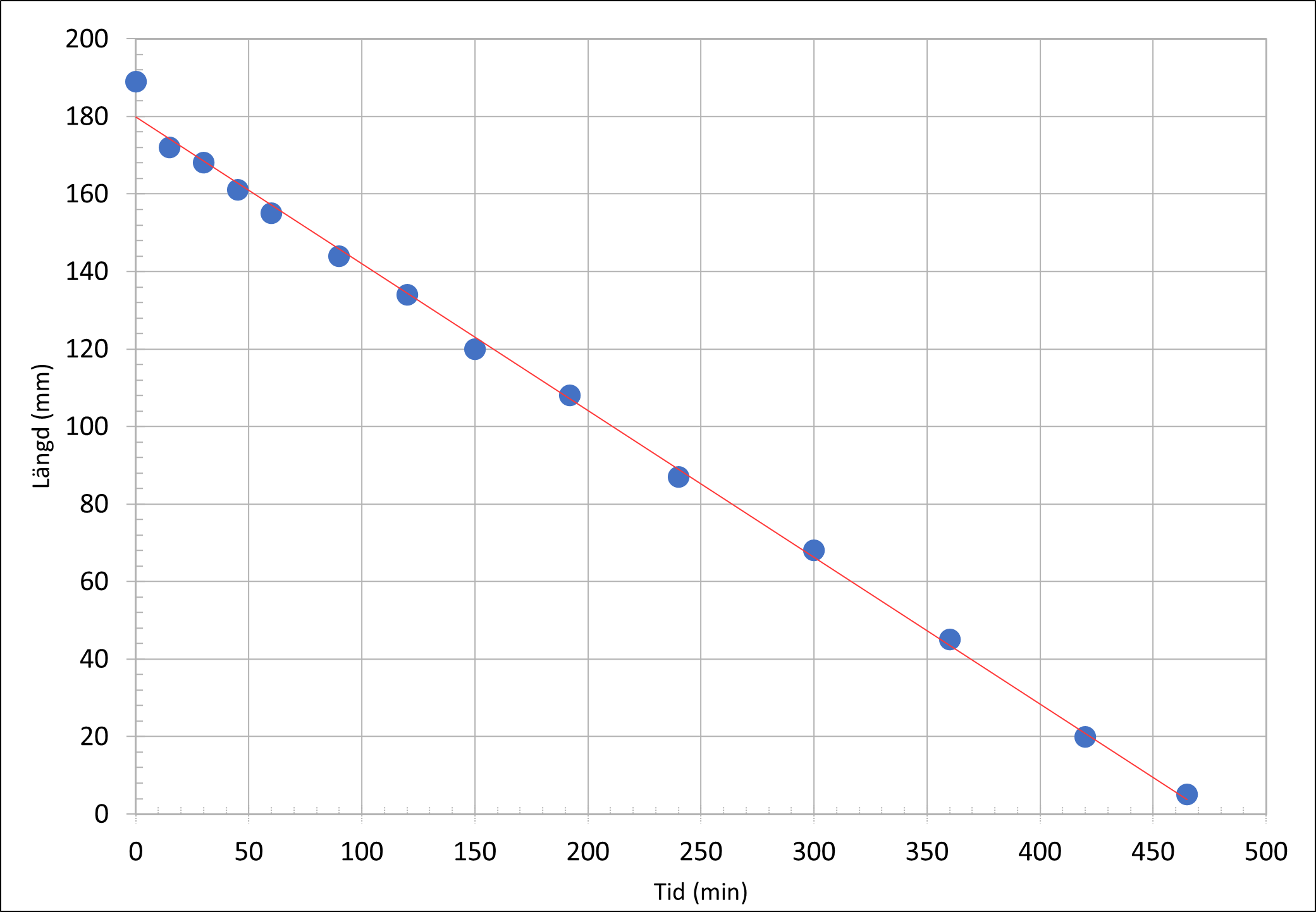
Ett stearinljus bränns och dess längd mäts som funktion av tiden det brunnit. Resultaten av mätningarna presenteras i material . I början är stearinljusets längd 189 mm, diameter 21 mm och medeldensitet 862 kg/m3.
5.1 Gör en grafisk presentation av stearinljusets längd som funktion av tiden. Visa i grafen materialets datapunkter och en lämplig anpassning till mätdata. 5 p.
Som modell får vi en rät linje vars ekvation är l(t) = 178mm - 0,37 t mm/min
Modellen passar bra till mätdata, förutom alldeles i början där stearinljusets diameter inte är konstant.
Poängsättning:
Det har gjorts en grafisk presentation där de uppmätta värdena för längden som funktion av tiden syns som enskilda mätpunkter. (3 p.) Som modell visas en rät linje som är enhetligt ritad i bilden, och linjens ekvation är given. (2 p.)
Om ett flertal enhetliga kurvor visas i bilden antas den sämsta vara modellen.
Om mätpunkterna inte markerats som enskilda punkter är avdraget 2 poäng.
Om storhetens beteckning eller enhet saknas eller axlarna är fel väg är avdraget för varje fel 1 poäng.
Typiskt fel:
Punkterna har sammanfogats med en bruten linje eller någon annan funktion än en rät linje har anpassats till dem.
5.2 Ett annat likadant stearinljus bränns i en vas full med vatten. Ljuset flyter i vattnet, som det visas i material . En metallring med massan 3,5 g är fäst som tyngd i ljusets bas för att ljuset ska hållas upprätt. Du kan anta att ringens volym är liten. Hur länge brinner stearinljuset i vasen? Du kan använda dig av kraftfiguren i material och den grafiska presentationen som du gjorde i deluppgift 5.1. 10 p.
Krafterna som påverkar stearinljuset är den sammanlagde tyngden G för ljuset och metallringen, och lyftkraften L. Krafterna är i jämvikt, G-L=0, eftersom ljuset flyter.
Stearinljusets massa får vi med hjälp av längden l, diametern D och densiteten \rho_l. Om ringens massa är m, får vi ljusets och ringens sammanlagda massa
M=\rho_l\frac{\pi D^2}{4}l+m.Den del av ljusets längd l som är under vattenytan betecknar vi med höjden h. Storleken av lyftkraften är lika stor som tyngden av vattnet som ljuset undantränger. Volymen av vattnet som ljuset tränger undan är V_v=h\frac{\pi D^2}{4} , alltså är storleken av lyftkraften \rho_v\frac{\pi D^2}{4}hg , där \rho_v är vattnets densitet. Vi märker att både G och N ändrar som funktion av tiden.
Genom att kombinera dessa med jämvikten av krafterna får vi \Bigl(\rho_l\frac{\pi D^2}{4}l+m\Bigr)g=\rho_v\frac{\pi D^2}{4}hg.
Stearinljusets längd minskar när ljuset brinner. Ljuset hamnar helt och hållet under ytan när ljusets och ringens sammanlagda tyngd är större än lyftkraften. Då är l = h, och ur jämviktsekvationen får vi \Bigl(\rho_l\frac{\pi D^2}{4}l+m\Bigr)g=\rho_v\frac{\pi D^2}{4}lg och vidare l=\frac{4m}{\pi D^2(\rho_v-\rho_l)}\approx {\rm 73,2}\,{\rm mm}.
Genom att avläsa från den grafiska presentationen ser vi att det här sker vid tidpunkten 280 minuter.
Poängsättning:
Utgående från Newtons II lag och med hjälp av skalär- eller vektorstorheter har en storhetsekvation skrivits för krafterna som verkar på ljuset. (2 p.)
Korrekta storhetsekvationer har givits för ljusets tyngd med hjälp ljusets och ringens sammanlagda massa (2 p.) och för lyftkraften där det omnämnts att densiteten är vattnets densitet. (2 p.)
Som svar för hur länge ljuset brinner har med 2-3 gällande siffrors noggrannhet givits 270 min – 280 min. (4 p.) För övrig noggrannhet är avdraget 1 poäng. Längden på ljuset när det sjunker bedöms inte, men ifall slutresultatet är fel kan korrekt längd vid stunden den sjunker ge 2 poäng.
Typiska fel:
Vektor och skalärer har använts blandat inom samma ekvation, lyftkraften har bestämts med hjälp av ljusets densitet, förkortningen av ljuset har glömts antingen i tyngdens eller lyftkraftens ekvationer.
6. En prasslande chipspåse 15 p.
Ett amerikanskt företag lanserade år 2010 en bionedbrytbar Sun Chips-potatischipspåse. Problemet med påsen var ett kraftigt prasselljud, vars intensitetsnivå nådde så högt som till 95 decibel. Vi antar att intensitetsnivån uppmättes på ett avstånd av 1,0 meter.
6.1 Vilken är intensitetsnivån då fem personer samtidigt prasslar med var sin chipspåse på 1,0 meters avstånd från en intensitetsnivågivare? 4 p.
Intensitetsnivån, L=10\,{\rm dB}\cdot\log\frac{I}{I_0} , beskriver styrkan av det registrerade ljudet, där I är den registrerade intensiteten och I_0=10^{-12}\,{\rm W/m}^{2} är en jämförelsenivå som motsvarar tröskeln för människans hörsel.
Intensitetsnivån för prasslet från en påse på avståndet en meter är L=10\,{\rm dB}\cdot\log\frac{I_p}{I_0}={\rm 95}\,{\rm dB} där I_p är prasslets intensitet.
Från det här får vi för prasslets intensitet I_p=10^{9,5}I_0=10^{-2,5}\,{\rm W/m}^2.
Om de som prasslar är fem till antalet blir intensiteten fem gånger så stor, alltså 5 I_p=5\cdot 10^{-2,5}\,{\rm W/m}^2.
Då är intensitetsnivån L={\rm 10}\,{\rm dB}\cdot\log\frac{5\cdot 10^{-2,5}\,{\rm W/m}^2}{10^{-12}\,{\rm W/m}^{2}}={\rm 102}\,{\rm dB}\approx {\rm 100}\,{\rm dB}.
Poängsättning:
Med 1-3 gällande siffrors noggrannhet har korrekt intensitet eller ljudnivå 100 dB – 102 dB givits som beräknad genom ett femfaldigande av intensiteten. (4 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiskt fel:
Ljudnivån från en påse har multiplicerats med fem.
6.2 Genom produktutveckling lyckades man sänka prasselljudets intensitetsnivå till 75 decibel. Hur många procent utgjorde då ljudets intensitet av den ursprungliga intensiteten? 3 p.
Från storhetsekvationen för intensitetsnivån ser vi att intensitetsnivån ökar med 10 dB när intensiteten blir tio gånger större, och intensitetsnivån ökar med 20 dB när intensiteten blir 100 gånger större. På motsvarande sätt minskar intensiteten till en hundradel när intensitetsnivån minskar med 20 dB. Efter produktutvecklingen är prasselljudets intensitet alltså 1,0 % av den ursprungliga intensiteten.
Poängsättning:
Med 1-2 gällande siffrors noggrannhet har som svar givits 1 %. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiskt fel:
Istället för intensitet har ljudnivåer jämförts.
6.3 Uppskatta på vilket avstånd den ursprungliga (95 dB) chipspåsens intensitetsnivå motsvarar vindsus med en intensitetsnivå på 30 dB. 5 p.
Intensitetsnivån för vindens sus kan skrivas i formen L_v=10\,{\rm dB}\cdot \log\frac{I_v}{I_0}=30\,{\rm dB}.
Från det här får vi susets intensitet I_v=10^3I_0=10^{-9}\,{\rm W/m}^{2}.
Intensiteten är omvänt proportionell mot kvadraten av avståndet. Då är \frac{I_p}{I_v}=\frac{r_v^2}{r_p^2} , ur vilket vi för avståndet kan lösa r_v=r_p\sqrt{\frac{I_p}{I_v}}={\rm 1,0}\,{\rm m}\,\sqrt{\frac{10^{-2,5}\,{\rm W/m}}{10^{-9}\,{\rm W/m}}}={\rm 1}\,{\rm 778,3}\,{\rm m}\approx {\rm 1,8}\,{\rm km.}
Poängsättning:
Ur lösningen framgår intensitetens 1/r2 -beroende utgående från geometrin. (2 p.)
Med 2-3 gällande siffrors noggrannhet har avståndet 1,8 km givits. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiskt fel:
En minskning i intensiteten har motiverats med storhetsekvation I = \frac{P}{A}, där A är ytan av en cirkel.
6.4 Varför är det beräknade avståndet i deluppgift 6.3 inte realistiskt för verkliga situationer? 3 p.
Ljudvågornas energi absorberas i luften och i alla hinder på vägen. Därmed dämpas ljudet effektivare än vid idealsituationen som beskrevs tidigare. Avståndet på vilket intensitetsnivån har dämpats till 30 dB är alltså i praktiken betydligt kortare än för idealsituationen som beräknades i deluppgift 6.3.
Poängsättning:
Som fenomen har absorption i luften eller hinder omnämnts. (3 p.) Ifall det här saknas kan reflektion i hinder ge 1 poäng.
Typiska fel:
Endast motiverat med avstånd, dämpning, eller buller.
7. En handdriven generator 15 p.
Bilden i material visar en handdriven generator. Då en spole inuti den permanenta magneten roterar med en konstant vinkelhastighet uppstår en periodiskt växlande spänning mellan den svarta och den röda ledningen som syns i bilden.
7.1 Förklara hur spänningen uppstår. 4 p.
Då spolen roterar förändras det magnetiska flödet genom den.
Det uppstår en växelspänning i spolen i enlighet med induktionslagen e = -N\frac{d\Phi}{dt}.
Poängsättning:
Det har berättats att det magnetiska flödet genom spolen förändras (2 p.) och att den här förändringen skapar en ström eller spänning. (2 p.)
Typiska fel:
Det påstods att magnetfältet förändras.
7.2 Härled ur induktionslagen uttrycket |e|=NBA\omega för toppvärdet på spolens inducerade spänning. I uttrycket är N antalet varv i spolen, B den magnetiska flödestätheten för den permanenta magneten, A spolens yta och \omega spolens vinkelhastighet. 4 p.
Det magnetiska flödet genom spolen är \Phi = BA \cos\varphi = BA \cos(\omega t) , där \varphi är vinkeln mellan magnetfältet och spolen och \omega är vinkelhastigheten för spolens rotation.
e = -N\frac{d\Phi}{dt} = NAB \omega\sin(\omega t) = NAB\omega(\sin\varphi)\sin\varphi får värden mellan -1…+1, alltså är toppvärdet för spänningen i motsvarande fall |e|=NAB\omega.
Poängsättning:
Storhetsekvationen för det magnetiska flödet har deriverats. (2 p.)
Toppvärdet har motiverats med maximum för sinus- eller cosinusfunktionen. (2 p.)
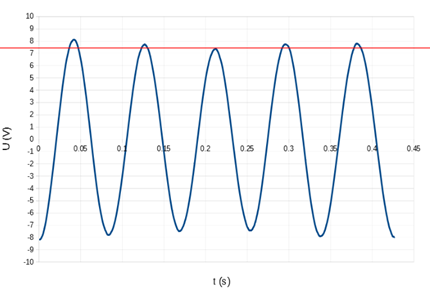
7.3 En simulering av spänningen som generatorn producerar finns i material . I simuleringen kan du reglera rotationshastigheten med vilken det stora draghjulet roteras och avläsa värden ur en Ut-graf, där U är spolens spänning. Den kvadratiska spolen har 150 varv och spolens sidolängd är 6 cm. Bestäm med hjälp av simuleringen den magnetiska flödestätheten vid spolens position. 7 p.
Ur ekvationen i deluppgift 7.2 kan vi lösa ett uttryck för den magnetiska flödestätheten: B=\frac{|e|}{NA\omega}=\frac{|e|}{Nr^2\frac{2\pi}{T}} , där T är växelspänningens periodtid och r är längden på spolens sida.
I exempelbilden är toppvärdet för spänningen ungefär 7,5 V och periodtiden 0,42 s / 5 = 0,084 s. Genom att sätta in de avlästa värdena och de värden som är givna i uppgiften får vi den magnetiska flödestätheten: B=\frac{\rm 7,5 V}{150\cdot (\rm 0,06 m)^2\frac{2\pi}{0,084 s}}={\rm 0,1857}\,{\rm T}\approx{\rm 0,2}\,{\rm T}.
Rotationshastigheten ska justeras så att det är möjligt att avläsa värden för spänningen och periodtiden från grafen med tillräckligt stor noggrannhet (ca 0,5...2,5 varv per sekund).
Poängsättning:
En graf har visats ur vilken toppvärdet för spänningen (2 p.) och periodtiden (2 p.) har avlästs.
En storhetsekvation har lösts för den magnetiska flödestätheten. (1 p.)
Med 1-2 gällande siffrors noggrannhet har den magnetiska flödestätheten givits som 0,18 T – 0,22 T. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Rotationshastigheten som matas in i simuleringen har använts för att bestämma periodtiden istället för att avläsa värdet från grafen.
8. Lilla Curie 15 p.
8.1 Artikel beskriver de mobila röntgenundersökningsapparater som användes under första världskriget. Varför kunde röntgenapparaterna vanligtvis inte kopplas direkt till det elektriska nätverket på den tiden? 2 p.
Det fanns inte elektricitet vid alla fältsjukhus. Dessutom varierade spänningen i Frankrikes elnät, och på en del ställen användes likspänning och på andra växelspänning.
Poängsättning:
Det har berättats att elektricitet inte fanns överallt. (1 p.)
Det har berättats att spänningens typ eller storlek varierade i olika områden. (1 p.)
Typiska fel:
Det påstods att spänningens typ eller storlek varierade med tiden.
8.2 Strålning kunde detekteras med en bildplatta eller ett fluoroskop. Ett fluoroskop består av en glasskiva som är överdragen med ett fluorescerande ämne, och genom den kunde man se en patients röntgenbild exempelvis på det sätt som visas i bild . Vid tiden för första världskriget var det motiverat att använda båda metoderna. Vilken metod skulle du själv använda i dagens läge och varför? 5 p.
Med ett fluoroskop såg läkaren skadorna på en fluorescerande skiva medan undersökningen utfördes. Det var snabbare och därför föredrogs det under första världskriget, men det ledde till en större strålningsdos för sjukhuspersonalen. Man utsattes för en särskilt stor strålningsdos om man opererade patienten samtidigt som röntgenundersökningen pågick, vilket sker i fotografi 8.B. Avbildning på en bildplatta krävde ett mörkrum för framkallningen. Diagnostiken var alltså långsammare. En fördel var ändå att det blev en permanent avbildning som man kunde använda också i ett senare skede.
Idag känner man bättre till nackdelarna med joniserande strålning. Man skulle lägga större vikt på att skydda sjukhuspersonalen och patienterna från strålningen, och därför skulle bildplattorna vara ett bättre val mot bakgrunden av nuvarande kunskap.
Poängsättning:
Bildplattan har valts. (2 p.)
Det har berättats att strålningsdosen från röntgenkällan är mindre då man använder bilplatta eller större då man använder fluoroskop. (3 p.) Poäng ges inte för motiveringen ifall svaret endast motiveras med en utsättning för strålningen.
Typiska fel:
Valet motiverades med at avbildningen var snabb eller långsam.
Det påstods att strålningen kommer från något annat än röntgenkällan.
8.3 Hur kommer det sig att skadorna som beskrivs i material eller olika lungsjukdomar kan observeras genom röntgenundersökningar? Material ger ett exempel på en röntgenbild av en influensapatient från år 1918. 8 p.
Kontrasten i röntgenbilden uppstår från skillnader i absorption. Röntgenstrålning är relativt högenergetisk elektromagnetisk strålning. Röntgenstrålning absorberas i materia i huvudsak genom att strålningen frigör elektroner från atomer. Olika grundämnen har olika antal elektroner. Mjuka vävnader består till största delen av föreningar bildade av grundämnen med låga ordningstal, såsom väte, kol och syre. Därför absorberar de mindre röntgenstrålning än benvävnader, som innehåller mycket kalcium, eller främmande föremål av metall. Genom röntgenundersökningar kan man alltså enklast upptäcka benbrott eller till exempel splitter. Skador i den mjuka vävnaden är svårare att se. Å andra sidan absorberas röntgenstrålning mycket dåligt av gaser eftersom gasers densitet är lägre än den mjuka vävnadens densitet. Genom röntgenundersökningar kan man då alltså även se om det har samlats vätska i lungorna i stället för gas.
Poängsättning:
Det har förklarats att skillnader observeras i strålningen som färdas genom kroppen. (2 p.) Poäng ges inte om det påstås att röntgenstrålarna reflekteras inne i patienten.
Det har förklarats att grundämnenas ordningstal påverkar hur ämnet absorberar eller dämpar strålningen. (2 p.)
Det har förklarats att ämnets densitet påverkar hur ämnet absorberar eller dämpar strålningen. (2 p.)
Ett par (exempelvis mjukvävnad och ben) som orsakar kontrast har omnämnts och det har förklarats att de kan urskiljas på grund av olika absorption. (2 p.)
Typiska fel:
Man svarade på frågan om vad som kan urskiljas med röntgenundersökningar. De uppvisade röntgenbilderna förklarades.
Del 3: 20-poängsuppgifter
9. Växelverkan mellan gammastrålning och materia 20 p.
En gammafoton, alltså en högenergetisk foton, växelverkar med materia på tre olika sätt. I bild presenteras den mest sannolika typen av växelverkan för en foton vid olika energier med grundämnen av olika ordningstal.
9.1 Vad händer med fotonen och vart överförs dess energi vid den fotoelektriska effekten och vid parbildning? 6 p.
I den fotoelektriska effekten försvinner fotonen och nästan all dess energi överförs till en elektron i mediet.
Vid parbildning försvinner fotonen då den (vanligtvis) skapar en elektron och en positron som mottar fotonens energi som massa och kinetisk energi. En del av fotonens energi (1 022 keV) omvandlas till massa hos elektronen och positronen.
Poängsättning:
Det har omnämnts att fotonen försvinner vid fotoelektrisk effekt (1 p.) och att dess energi övergår till en elektron. (2 p.)
Det har omnämnts att fotonen försvinner eller omvandlas till materia vid parbildning (1 p.) och att dess energi övergår till partikel-antipartikelparet. (2 p.)
9.2 Vid Comptonspridning sprids en foton efter växelverkan med en elektron. Fotonens energi efter spridningen är E^\ast=\frac{E}{1+\frac{E}{m_ec^2}(1-\cos\theta)} där E är den ursprungliga fotonens energi, \theta är spridningsvinkeln och m_e är elektronens massa. Vilken är den största rörelseenergi som en elektron kan få från en foton när en foton på 662 keV sprids från den? 6 p.
Utgående från den totala energins bevarande är den kinetiska energin som elektronen får lika stor som fotonens energiförändring, alltså E_e=E-E^\ast.
Fotonens energiförändring är som störst då \theta är 180°, eftersom E^\ast då får sitt minsta värde. Vi får
E_e=E-E^\ast = E-\frac{E}{1+\frac{2E}{m_ec^2}}=E\biggl(1-\frac{1}{1+\frac{2E}{m_ec^2}}\biggr)={\rm 662}\,{\rm keV}\biggl(1-\frac{1}{1+\frac{2\cdot {\rm 662}\,{\rm keV}}{{\rm 511}\,{\rm keV}}}\biggr)={\rm 477,65}\,{\rm keV}\approx {\rm 478}\,{\rm keV}.
Poängsättning:
Korrekt storhetsekvation för elektronens energi har skrivits med hjälp av fotonernas energi. (2 p.)
Det har konstaterats när fotonens energi är som minst eller fotonens minsta energi har beräknats. (2 p.)
Elektronens energi har givits med 3 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Det har tänkts att fotonens energi är som minst då vinkeln är 90˚.
Det har tänkts att den spridda fotonens energi är 662 keV. Sådan Comptonspridning kan inte förekomma, eftersom den spridda fotonens energi högst kan vara hälften av elektronens viloenergi. Om man försöker lösa den ursprungliga fotonens energi med den givna ekvationen får man en imaginär lösning.
9.3
Med två olika detektorer med liten volym observerade man gammastrålning på 662 keV som producerats av en Cs-137-strålkälla. Den ena detektorn var gjord av plast medan den andra innehöll vismut, germanium och syre. Energispektrumen som producerades med detektorerna är presenterade i bild , där N är antalet registrerade händelser vid olika energier.
Båda detektorerna är så kallade scintillationsräknare, i vilka en jonisering orsakad av laddade partiklar som färdas snabbt skapar synligt ljus. Mängden ljus som skapas är proportionell mot den joniserande partikelns rörelseenergi. Detektorerna observerar alltså inte gammastrålningen direkt, utan i stället den indirekta joniseringen orsakad av strålningen.
Förklara vad som mest troligt skett i detektorn då händelser i spektrumen uppenbarat sig i området under 400 keV. Vad har mest troligt skett i detektorn för spektrum A i bild då en händelse i spektrumet har uppenbarat sig vid ungefär 660 keV? Vilket av spektrumen (A/B) i bild är spektrumet från detektorn gjord av plast? Du kan anta att gammafotonen växelverkar endast en gång i detektorn.
8 p.
Eftersom gammafotonens energi är mindre än 1 022 keV kan parbildning inte ske. I alla situationer överförs en del eller all energi från fotonen till en elektron. Elektronen joniserar materian i detektorn, och då skapas det synligt ljus.
Ifall gammafotonen växelverkar genom Comptonspridning i detektorn kommer elektronen i enlighet med föregående deluppgift att få mindre än 500 keV energi (elektronen absorberas i detektorn). Om spridningsvinkeln är mindre kommer elektronen att få ännu mindre energi. Händelserna i området under 400 keV uppstår när en foton genomgår Comptonspridning i detektorn.
Om fotonen växelverkar genom den fotoelektriska effekten kommer hela dess energi att registreras när elektronen absorberas i detektorn. Det här motsvarar toppen i spektrumet där energin är lika stor som fotonens energi.
Spektrum B kommer från detektorn gjord av plast. Plast består främst av kol och väte, vars ordningstal är låga. Enligt bild 9.A växelverkar en gammafoton på 662 keV närmast genom Comptonspridning i detektorn, varvid endast händelser under 500 keV registreras. Det genomsnittliga ordningstalet för vismut-germanium-syre-detektorn är högre, alltså kan också totalabsorption genom den fotoelektriska effekten märkas vid 660 keV.
Poängsättning:
Signalen som syns vid under 400 keV i detektor B har kopplats till Comptonspridning. (2 p.)
Signalen som syns vid 662 keV i detektor A har kopplats till den fotoelektriska effekten. (2 p.)
Som detektorn av plast har valts B (2 p.) och valet har motiverats genom att jämföra ordningstalen för grundämnena i plast och i BiGeO-detektorn och kopplat dem till sannolikheterna för Comptonspridning och fotoelektrisk effekt. (2 p.).
10. Smältvärme för paraffin 20 p.
Du vill experimentellt bestämma den specifika smältvärmen för ett material på en fysiklektion. Din uppgift är att planera en så enkel mätuppställning som möjligt samt behandlingen av resultaten från den.
Som material har du valt paraffin, vars smältpunkt är 60 °C. För en enkel experimentell uppställning har du följande utrustning till ditt förfogande:
- ett kärl av cellulär polystyren (alltså ett styrox-kärl)
- vatten från en kran och en vattenkokare vars effekt är okänd
- paraffin i fast form vid rumstemperaturen 20 °C
- en sax, en pincett, tejp, plastpåsar, aluminiumfolie
- en begränsad tabellbok ur vilken du får information om vattnets egenskaper med tillräckligt stor noggrannhet, men ingen information om paraffinet.
Utöver utrustningen ovan har du i fysiksalen endast tillgång till följande redskap:
- en klocka
- ett skjutmått
- en termometer
- ett mätglas
- en våg
- en specifik gravitetsmätare
- en fuktmätare
- ett aluminiumkärl med tunna väggar.
10.1
Vilka är huvudmomenten i experimentet och vilka mätningar utförs under dem? Hur bestämmer du paraffinets specifika smältvärme utifrån mätresultaten?
Presentera de storhetsekvationer som behövs. Om en grafisk presentation behövs för att bestämma resultatet, skissera då en sådan med de mätdata du antar att du skulle få. Vid behov kan du använda dig av mallen för en graf i material .
Vilka redskap från den numrerade listan behöver du för det här experimentet? Gör upp en lista.
14 p.
Det väsentliga är att mäta värmemängden som det heta vattnet avger till paraffinet under smältningen. Innan paraffinet kan smältas måste det värmas upp till smältpunkten.
Vatten värms upp till kokpunkten i vattenkokaren.
Paraffinstycket vägs (massa m_{\rm p}) och läggs i styrox-kärlet. (Paraffinstycket kan antingen vara i aluminiumkärlet med tunna väggar eller i aluminiumfolie som placeras i styrox-kärlet. Det heta vattnet hälls bredvid det. På det här sättet blandas paraffinet aldrig med vattnet. Det här är inte nödvändigt, men det gör allting mindre kladdigt.) Hett vatten tas från kokaren (möjligen med mätglaset) i små mängder. Vattnets massa och utgångstemperatur T0 mäts och det hälls in i styrox-kärlet. Sluttemperaturen mäts efter att man väntat en stund och låtit temperaturerna jämna ut sig. Temperaturen som mäts på det här sättet motsvarar både vattnets och paraffinets temperatur.
En liten mängd vatten, vars massa har mätts och vars utgångstemperatur man har försökt få till T0, läggs till. Systemets temperatur får jämna ut sig och mäts sedan. Tilläggandet av vattnet upprepas och samma storheter mäts. Temperaturen för vattnet stiger varje gång, vilket motsvarar uppvärmningen av paraffinstycket. I något skede uppnår vi smälttemperaturen 60 ˚C. I det här skedet börjar den del av mätningen som kan utnyttjas, och under vilken systemets sluttemperatur inte stiger trots att vatten tillförs.
Vi fortsätter tillföra mera vatten i omgångar ända tills vi märker att temperaturen igen börjar stiga. I det här skedet har allt paraffin smält och mätningen kan slutföras.
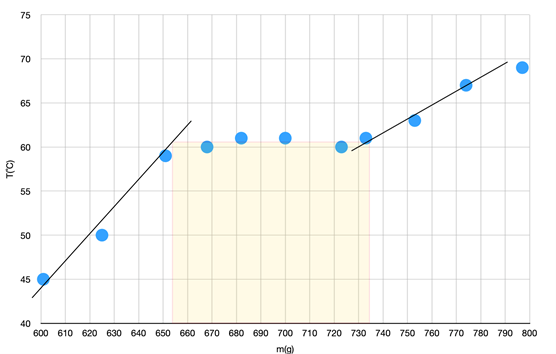
Som mätresultat får vi sluttemperaturen T som funktion av vattnets massa m. Vi ritar en (m,T)-graf som bör se ut ungefär som bilden ovan. Utgående från den grafiska presentationen kan vi bestämma från och med vilken massa M_b på vattnet temperaturen hålls konstant och vid vilken massa M_s temperaturen igen börjar stiga. Med hjälp av skillnaden mellan de här massorna \Delta M = M_s – M_b kan vi bestämma värmemängden Q=c\Delta M\Delta T, där c är vattnets specifika värmekapacitet, som överförs från vattnet till paraffinet. Temperaturskillnaden är\Delta T=T_0-{\rm 60}\,^{\rm o}{\rm C}.
Den här värmemängden går åt till att smälta paraffinet, alltså Q=sm_p.
Från det här får vi smältvärmen för paraffin s=c\Delta M\Delta T/m_p.
Från den numrerade listan av utrustning behövdes en våg för att mäta vattnets och paraffinets massa och en termometer för att mäta vattnets temperatur. Vid mätningarna kan man även använda en klocka, ett mätglas och aluminiumkärlet med tunna väggar, utöver onumrerad utrustning.
Även andra metoder kan presenteras som lösning. Som variation till metoden ovan kan hela mängden vatten läggas till på en gång om experimentet sedan upprepas tillräckligt många gånger med olika mängder vatten. Paraffinet kan även smältas i vattenkokaren så att det finns vatten i kokaren och paraffinet är i aluminiumkärlet inne i kokaren. Då ska även en metod för att bestämma vattenkokarens effekt beskrivas.
Lösningarna bedömdes genom att klassificera dem i fyra olika grupper:
A. En bestämning av smältvärmet lyckas väl.
B. En bestämning av smältvärmet kan lyckas men metoden är inexakt eller opraktisk. Poäng kan ges för utrustningen och storhetsekvationerna.
C. Smältvärmet bestäms på ett sätt som inte kan ge rätt svar. Poäng ges för utrustningen och högst en storhetsekvation.
D. Inget bestäms eller någon annan storhet än smältvärmet bestäms. Poäng ges endast för utrustningen.
Poängsättning:
Ur listan med numrerad utrustning har vågen (2 p.) och termometern (2 p.) omnämnts. Om det har påståtts att skjutmåttet, en specifik gravitetsmätare eller en fuktmätare behövs är avdraget 1 poäng för varje av dem.
Det har förklarats hur storhetsekvationerna Q_v=c_v\Delta M_v\Delta T_v och Q_s=s_p m_p används för att bestämma smältvärmet. (2 p.) + (2 p.) Utöver ekvationerna krävs det att de använda storheterna definieras och att det beskrivs hur de uppmäts.
En storhetsekvation för paraffinets smältvärme har givits med hjälp av de uppmätta storheterna. (2 p.)
En bra metod för att bestämma paraffinets smältvärme har beskrivits. (4 p.) Till en bra metod hör exempelvis att temperaturen mäts vid termisk jämvikt.
Typiska fel:
Smältpunkten bestäms i stället för smältvärmet (typ D).
Det har inte tagits i beaktande att paraffinet först måste värmas upp till smälttemperaturen eller så har det vätskeformade paraffinet värmts upp (typ C).
Paraffinet smälts med vatten vars temperatur är 60˚C (typ C).
Stora mängder vatten läggs på en gång till styrox-kärlet och vattnets temperatur mäts samtidigt som den hela tiden ändrar. Sedan används vattnets temperatur då smältningen börjar och slutar (typ B).
10.2 Till sist jämför du det värde på smältvärmen som du får från dina mätningar med litteraturvärdet. Nämn tre viktiga faktorer som orsakar en avvikelse mellan ditt uppmätta värde och litteraturvärdet. 6 p.
Exempel på verkliga felkällor
- fel eller inexakt vägning av massorna
- temperaturvariationer för det heta vattnet
- värmeförluster under smältprocessen
- svårigheter att bestämma början och slut för smältningen (tillsatsen av vattnet i omgångar)
Poängsättning:
Det har omnämnts värmeförluster i någon process. (2 p.)
Det har omnämnts en oklarhet i observationer av smältningens början eller slut eller i termiska jämvikten. (2 p.)
Det har omnämnts ett fel i samband med en namngiven mätning eller mätutrustning. (2 p.)
Typiska fel:
Aluminiumkärlets värmekapacitet, variationer i laboratoriets temperatur eller lufttryck, systematiska fel, räknefel, avsaknad av upprepade mätningar, orenheter eller obestämda mätfel påstås vara felkällor.
11. Rymdteleskopet James Webb 20 p.
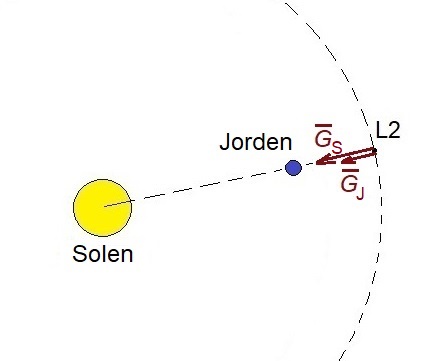
På juldagen 2021 avfyrades en Ariane 5-bärraket från Franska Guyana för att skicka rymdteleskopet James Webb (bild ) till Lagrangepunkten L2 i sol-jordsystemet. Placerad i den här punkten kretsar teleskopet runt solen så att det nästan hålls på en rät linje som går rakt igenom solen och jorden (bild ). Teleskopet rör sig på ett konstant avstånd från jorden så att solen och jorden alltid är på samma sida från teleskopet sett. Rymdteleskopet James Webb fungerar huvudsakligen i det infraröda området. Med hjälp av teleskopet kan man undersöka bland annat universums mest avlägsna platser och planeter i andra solsystem.
11.1 Rymdteleskopet James Webb placerades i rymden där dess temperatur kunde fås så låg som möjligt. Varför är en låg temperatur en avgörande faktor vid observation av infraröd strålning? 3 p.
Vid observation av infraröd strålning kan den infraröda strålningen som teleskopet själv producerar störa mätningarna och därför måste den elimineras så grundligt som möjligt. Det här görs genom att observationsinstrumenten hålls vid en mycket låg temperatur.
Poängsättning:
Teleskopets egen värmestrålning har omnämnts. (3 p.).
Typiska fel:
Man svarar att teleskopets temperatur bör vara låg.
Som orsak omnämns omgivningens värmestrålning.
11.2 Varför består värmeskyddet som syns i bild av fem separerade lager, i stället för bara ett enhetligt lager? 4 p.
Om värmeskyddet var ett enhetligt lager, skulle värme komma åt att överföras genom det via ledning. Ledning av värme genom vakuumet mellan värmeskyddets olika lager är inte möjlig.
Poängsättning:
Värmets ledning i ett lager har omnämnts. (2 p.)
Det har nämnts att vakuumet mellan lagren inte leder värme eller att värmet sprids mellan lagren endast genom strålning. (2 p.)
Funderingar gällande strukturens tyngd varken ger poäng eller leder till poängavdrag.
Typiska fel:
Det påstås att luften mellan lagren inte leder värme.
Det påstås att fem lager isolerar bättre än ett lager.
Man besvarar frågan om varför teleskopet har ett värmeskydd.
11.3 Rita en kraftfigur för teleskopet och namnge krafterna. 4 p.
I kraftfiguren är \bar{G}_{\rm S} och \bar{G}_{\rm J} gravitationskrafterna som påverkar rymdteleskopet från solen respektive jorden. Gravitationskraften som solen påverkar teleskopet med är riktat mot solen och gravitationskraften som jorden påverkar teleskopet med är riktat mot jorden. Krafterna är nästan likriktade. En noggrannare analys visar att den beskrivna cirkelbanan är instabil, alltså rör sig teleskopet i praktiken i området kring L2, och bankorrigeringar är nödvändiga. Det här tas inte i beaktande i svaret.
Poängsättning:
Kraftfiguren visar satelliten och de två krafter som påverkar den. Krafterna har namngivits som solens och jordens gravitationskrafter och deras symboler (skalärer eller vektorer) har visats i figuren. Krafternas riktningar ska vara antingen mot solen och jorden som syns i figuren eller vinkelrät mot tangenten av cirkelbanan som visas med en båge. (4 p.)
Poäng ges inte om riktningen för någon kraft är fel eller inte framgår eller om storhetssymbolen saknas. Om figuren innehåller krafter som verkar på solen eller på jorden, andra överflödiga krafter eller hastighet- eller accelerationsvektorer som är fast i satelliten så ges inga poäng.
Avdraget är 1 poäng om krafterna inte namngivits som gravitationskrafter.
Typiska fel:
Det framgår inte i figuren var solen och jorden är, alltså är krafternas riktning inte fastslagen. Krafter som verkar på jorden eller solen har betecknats i figuren.
11.4 Teleskopets avstånd från jorden är 1,5 miljoner kilometer. Bekräfta det här genom att visa att Newtons andra lag uppfylls för det här värdet på avståndet. 9 p.
Gravitationskonstanten, solens massa, jordens massa, avståndet mellan solen och jorden samt omloppstiden för jorden och rymdteleskopet runt solen är
\gamma={\rm 6,674}\cdot{\rm 10}^{\rm -11}\,\frac{{\rm Nm}^2}{{\rm kg}^2} m_{\rm S}={\rm 1,989}\cdot{\rm 10}^{\rm 30}\,{\rm kg}, m_{\rm M}={\rm 5,974}\cdot{\rm 10}^{\rm 24}\,{\rm kg} r={\rm 1,4960}\cdot{\rm 10}^{\rm 8}\,{\rm km}, T={\rm 365,2}\,{\rm d}Newtons andra lag för rymdteleskopet placerat i Lagrangepunkten L2 är ma=G_{\rm S}+G_{\rm J} där m är teleskopets massa, a teleskopets normalacceleration och G_{\rm S} och G_{\rm J} är gravitationskrafterna med vilka solen och jorden påverkar teleskopet. Vi sätter in dem i ekvationen a=\frac{v^2}{r+d}=\frac{[2\pi(r+d)/T)]^2}{r+d}=\Bigl(\frac{2\pi}{T}\Bigr)^2(r+d) där v är teleskopets hastighet och d är avståndet från L2 till jorden, och G_{\rm S}=\gamma\frac{m_{\rm S}m}{(r+d)^2}, G_{\rm J}=\gamma\frac{m_{\rm J}m}{d^2}, och förkortar bort teleskopets massa. Då får vi \Bigl(\frac{2\pi}{T}\Bigr)^2(r+d)=\gamma\Bigl(\frac{m_{\rm S}}{(r+d)^2}+\frac{m_{\rm J}}{d^2}\Bigr)
Vi visar att det här gäller för d = 1,5 ∙ 106 km. Genom att sätta in värden för storheterna får vi som svar på ekvationens vänstra sida 5,9915\cdot 10^{-3}\,\text{m/s}^2 och högra sida 5,9914\cdot 10^{-3}\,\text{m/s}^2. De här värdena är med tillräckligt stor noggrannhet lika stora, alltså uppfylls Newtons andra lag med det givna värdet på d.
Poängsättning:
En storhetsekvation ma=G_{\rm S}+G_{\rm J} i enlighet med Newtons II lag har presenterats för krafterna som påverkar satelliten. (2 p.)
En storhetsekvation för satellitens normalacceleration har visats, och radien för banan som använts i den har berättats vara satellitens avstånd till solen. (2 p.) Solens och jordens radier kan läggas till avståndet, eftersom felet som uppstår från dem är marginellt litet.
Teleskopets banhastighet har lösts med hur den gör ett varv runt solen en gång per år eller dess vinkelhastighet har lösts med hur den är i omlopp runt solen med samma vinkelhastighet som jorden. (2 p.)
Med antagandet att alla tidigare nämnda saker är korrekta konstateras det accelerationerna på höger och vänster sida i ekvationen är lika stora när man substituerar för de kända storheternas värden (2 p.) och att Newtons II lag därmed gäller. (1 p.)
Typiska fel:
Gravitationen förorsakad av antingen jorden eller solen har glömts. Omloppsbana går runt jorden i stället för runt solen.