Beskrivningar av goda svar: SV – Fysik
13.9.2023
Slutgiltiga beskrivningar av goda svar 9.11.2023
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
Del 1: 20-poängsuppgift
1. Flervalsuppgifter från olika delområden i fysiken 20 p.
Välj det alternativ som passar bäst för varje situation i deluppgifterna 1.1–1.10. Rätt svar ger 2 p., fel svar 0 p. och inget svar 0 p.
1.1 Fission och fusion är kärnreaktioner som kan utnyttjas vid energiproduktion. Vilket av följande påståenden är korrekt? 2 p.
- Vid fusion förenas två lätta kärnor, och vid fission spjälkas en tung kärna. (2 p.)
1.2 Du sätter dig i en het bastu på en lave av trä där huvudet av en metallspik sticker upp. I jämförelse med laven känns spiken mycket mer brännande mot din hud eftersom 2 p.
- spikens värmeledningsförmåga är större än lavens. (2 p.)
1.3 En bil drar en husvagn och framskrider med en jämn fart på en vågrät motorväg. Summan av krafterna som påverkar husvagnen 2 p.
- är noll. (2 p.)
1.4 Diametern på en tjock metalltråd är dubbelt så stor som diametern på en tunn tråd. Trådarna är lika långa. Resistansen hos den tunna tråden är R. Den tjocka trådens resistans är 2 p.
- \tfrac{1}{4}R. (2 p.)
1.5 Du färdas med båt raka vägen från Helsingfors till Tallinn. Du färdas exakt halva sträckan med hastigheten v och resten av vägen med hastigheten 2v. 2 p.
- Din medelhastighet på hela sträckan är \tfrac{4}{3}v. (2 p.)
1.6 I ett akvarium flyter en leksaksbåt av plast och i båten ligger en sten. Då stenen flyttas från båten till akvariets botten kommer vattennivån i akvariet att 2 p.
- sjunka. (2 p.)
1.7 En låda glider på ett bord och friktion saktar ner dess fart. Arbetet som friktionskraften utför 2 p.
- är negativt. (2 p.)
1.8 Jordens rotationsaxel lutar med 23 ° i förhållande till normalen för ytan av ellipsen som omloppsbanan sveper (bild). Om lutningsvinkeln i stället var 0 ° skulle 2 p.
- årstider inte förekomma på jorden. (2 p.)
1.9 Då en batteridriven lampa tänds 2 p.
- förändras inte den totala elektriska laddningen i batteriet. (2 p.)
1.10 En flaskborste har skjutits in i ett plaströr underifrån (bild). På grund av en liten friktionskraft hålls borsten kvar i röret. Då man slår snabbt och kraftfullt på rörets övre ända med en gummihammare rör sig röret neråt. Till följd av slaget rör sig borsten 2 p.
- uppåt i förhållande till röret. (2 p.)
Del 2: 15-poängsuppgifter
2. Pirttikoski 15 p.
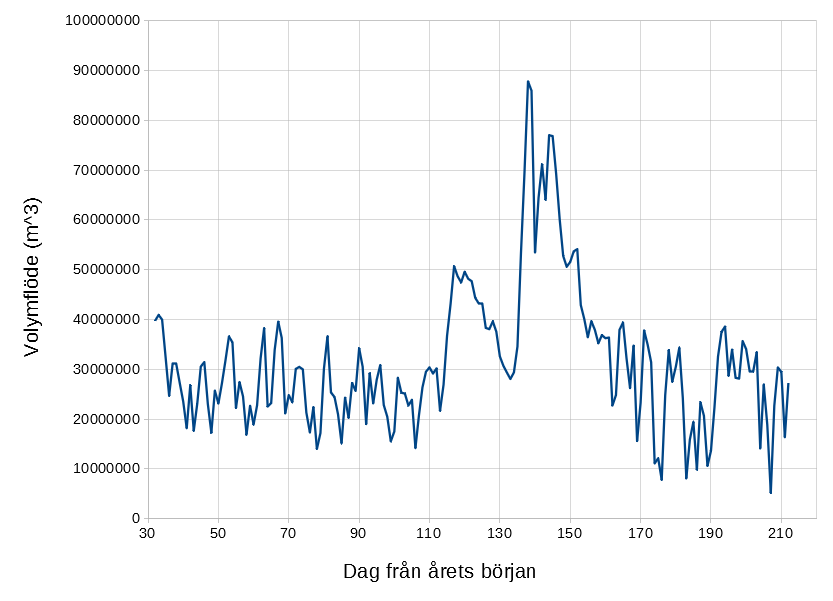
2.1 Presentera volymen av vattnet som flödat under ett dygn som funktion av antalet dagar från början av året. 5 p.
Volymen av vattnet som flödat under ett dygn får vi genom att multiplicera dygnsmedelvärdet för volymflödet med antalet sekunder i ett dygn. Resultatet presenteras som funktion av antalet dagar från början av året:
Poängsättning:
Det har presenterats en graf över volymen av vattnet som flödat under ett dygn som funktion av antalet dagar från början av året. (5 p.)
I det här fallet är en bruten linje den bästa presentationsformen, men även histogram godkänns. Ifall endast punkterna har ritats och vattnets mängd inte kan avläsas specifikt för varje dag, eller ifall en orimlig anpassningskurva har ritats till hela datamängden, är avdraget 1 poäng.
Om den ena eller båda av axlarnas siffervärden saknas, eller om axlarna är fel väg, är avdraget 2 poäng.
Om endera axeln saknar beteckning eller är betecknad på ett inkonsekvent sätt, eller om enheten för en axel är fel eller saknas, är avdraget för varje fel 1 poäng.
Om dygnsmedelvärdet eller systematiskt felberäknade värden har presenterats i stället för den totala volymen av vattnet som flödat under ett dygn är avdraget 2 poäng. Om datumet har använts på den vågräta axeln är avdraget 1 poäng.
Typiska fel:
Dygnsmedelvärdet har ritats som funktion av antalet dagar från årets början eller som funktion av datumet.
2.2 Under vilken månad var volymflödet som störst och vad var den totala volymen av vattnet som flödade under den månaden? 5 p.
Genom grafisk integrering eller genom att addera de dagliga flödena får vi det månatliga volymflödet:
| Månad | Volymflöde (kubikmeter) |
| Februari | 772692480 |
| Mars | 804322656 |
| April | 867906144 |
| Maj | 1606818816 |
| Juni | 939117888 |
| Juli | 749441376 |
I tabellen ser vi att det högsta månatliga volymflödet var i maj, ungefär 1,6 ⋅ 109 kubikmeter.
Poängsättning:
Grafisk integrering eller summering genom tabellberäkning har omnämnts eller syns i bilderna i svaret för den här deluppgiften. (2 p).
Som svar har givits rätt månad (1 p.) och med 2 – 5 gällande siffrors noggrannhet det korrekta volymflödet 1,5 – 1,7 km3. (2 p.) För övrig noggrannhet eller fel vid enhetsomvandling är avdraget 1 poäng.
Typiska fel:
Som svar har det givits 18000 m3/s eller 1,6 Gm3.
2.3 I Pirttikoski kraftverk faller vattnet 26 m. Hur mycket energi skulle kraftverket som mest ha producerat 13.3.2022 om hela den potentiella energin för vattnet som flödade genom kraftverket kunde ha utnyttjats? 5 p.
Energiproduktionen från kraftverket kan inte vara högre än förändringen i potentiell energi för det flödande vattnet. Den 13:e mars var vattnets volymflöde 30 087 072 kubikmeter och motsvarande förändring i den potentiella energin var
\Delta E_p=mg\Delta h =\rho Vg\Delta h=1000\,\frac{\rm kg}{{\rm m}^3}\cdot 30087072\,{\rm m}^3 \cdot 9,81\frac{\rm m}{{\rm s}^2}\cdot 26\,{\rm m}=7674008584320\,{\rm J}\approx 7,7\,{\rm TJ}.
Poängsättning:
En storhetsekvation för potentialenergin har givits och ur lösningen framgår det vilken massa det är frågan om. (2 p.)
Med 2 – 3 gällande siffrors noggrannhet har rätt svar givits inom intervallet 7,6 – 7,8 TJ. (2p.)
För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Beräkningarna har gjorts med dygnsmedelvärdet och som svar har givits 89 MJ.
3. Fasövergång 15 p.
Då termometerns utslag inte längre förändras är vattnet och isen sinsemellan i jämvikt, alltså är temperaturen vid den stunden T = 0 ℃
Efter att isbiten läggs i vattnet börjar isen värmas upp och vattnet kylas ner. För isens uppvärmning och vattnets nerkylning tillämpar vi ekvationen Q=cm\Delta T. I slutskedet är T=0\,^\circ{\rm C}, alltså för isen är \Delta T_{\rm i}=+18\,{\rm K} och för vattnet är \Delta T_{\rm v}=-1,0\,{\rm K}.
Isens uppvärmning till noll grader: värmet som överförs till isen är Q_{\rm i}=c_{\rm i}m_{\rm i}\Delta T_{\rm i}\approx (2090\,{\rm J/kg\,K})\cdot 0,05\,{\rm kg}\cdot 18\,{\rm K}=1881\,{\rm J}. Vattnets nerkylning till noll grader: värmet som överförs från vattnet är Q_{\rm v}=c_{\rm v}m_{\rm v}\Delta T_{\rm v}\approx (4182\,{\rm J/kg\,K})\cdot 0,40\,{\rm kg}\cdot (-1.0\,{\rm K})=-1673\,{\rm J}.
Eftersom systemet är isolerat ska summan av alla värmemängder bli noll (den totala energin bevaras). Vi märker att Q_{\rm i}+Q_{\rm v}>0.
Därmed behöver vi alltså en fasövergång som är kopplad till värmet
Q_{\Delta \rm{m}}
så att
Q_{\rm i}+Q_{\rm v}+Q_{\Delta \rm{m}}=0
, alltså är
Q_{\Delta \rm{m}}=-Q_{\rm i}-Q_{\rm v}\approx -1881\,{\rm J}+1673\,{\rm J}=-208\,{\rm J}.
Q_{\Delta \rm{m}}
är negativ, alltså måste en del av vattnet frysa. Då vattnet fryser avger det värmemängden
Q=-Q_{\Delta \rm{m}}\approx 208\,{\rm J}.
Vi beräknar det frysande vattnets massa
\Delta m.
Q=s\Delta m, alltså är \Delta m=Q/s\approx 208\,{\rm J}/(334\,{\rm J/g})\approx0,623\,{\rm g}.
Isbitens massa ökar och förändringen är alltså \Delta m\approx 0,62\,{\rm g}.
Endast en liten del av vattnet fryser, vilket betyder att det i slutskedet faktiskt finns både vatten och is i behållaren.
Poängsättning:
Som svar för sluttemperaturen har givits 0˚C. (3 p.) Ifall enheten har givits som grader, C eller ˚K är avdraget 1 poäng.
Storhetsekvationen Q=cm\Delta T har kopplats till lösningen (2 p.), och den har för lösningens del använts på korrekt sätt. (2 p.) Storhetsekvationen Q=sm har kopplats till lösningen (2 p.) Energins bevarande har på rätt sätt tillämpats de tre ovanstående värmemängderna. (2 p.)
Det har poängterats att isbitens massa ökar (2 p.), och rätt slutresultat har givits med 2 – 3 gällande siffrors noggrannhet inom intervallet 0,61 g – 0,63 g. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Frysningen av vattnet har glömts och som sluttemperatur har det erhållits en temperatur strax under 0˚C.
4. Flervalsuppgifter om strömkretsar 15 p.
Det finns tre strömkretsar i bild . Alla spänningskällor, motstånd och ledningar är ideala och sinsemellan identiska. Välj i varje deluppgift det alternativ som beskriver situationen bäst. Rätt svar 2 p. eller 3 p., fel svar 0 p., inget svar 0 p.
Om du har påbörjat uppgiften men bestämmer dig för att inte lämna in den för bedömning ska du ange ”Jag svarar inte” i var och en av deluppgifterna.
4.1 Fyra punkter A–D är markerade på ledningarna i strömkrets 1. Vi undersöker potentialerna i punkterna A, B, C och D. Där gäller 2 p.
- V_A=V_B>V_C=V_D (2 p.)
4.2 Vi undersöker den elektriska strömmen i punkterna A–D i strömkrets 1. Där gäller 2 p.
- I_A=I_B=I_C=I_D (2 p.)
4.3 Jämför storleken på de elektriska strömmarna i punkten C i strömkrets 1 och punkten G i strömkrets 2. Där gäller 2 p.
- I_G=\tfrac{1}{2}I_C (2 p.)
4.4 Jämför potentialerna i punkten C i strömkrets 1 och punkten G i strömkrets 2. Där gäller 2 p.
- V_G>V_C (2 p.)
4.5 Jämför storleken på de elektriska strömmarna i punkten C i strömkrets 1 och punkten M i strömkrets 3. Där gäller 2 p.
- I_M=I_C (2 p.)
4.6 Jämför storleken på de elektriska strömmarna i punkten E i strömkrets 2 och punkten K i strömkrets 3. Där gäller 2 p.
- I_E=\tfrac{1}{4}I_K (2 p.)
4.7 Hur förhåller sig de förbrukade elektriska effekterna i strömkretsarna 1, 2 och 3 till varandra? 3 p.
- P_3>P_1>P_2 (3 p.)
5. En bilresa 15 p.
5.1 Hur många fler liter bensin förbrukas på turresan än på returresan? 9 p.
På turresan förbrukas bränslets energi för att öka bilens potentiella energi och för arbetet som motståndskrafterna utför.
E_{\rm tur}=\Delta E_p+W=mg\Delta h+W
På returresan förbrukas bränslets energi fortfarande för att övervinna arbetet som motståndskrafterna utför, men den potentiella energin minskar.
E_{\rm retur}=-mg\Delta h+W
Skillnaden mellan energiförbrukningen på tur- och returresorna är
\Delta E=E_{\rm tur}-E_{\rm retur}=2mg\Delta h=2\,762\,496\,{\rm J}.
Energin produceras genom att bensin förbränns
\Delta E=\eta H\Delta V,där \eta är motorns verkningsgrad och H är bensinens värmevärde. Skillnaden mellan bensinförbrukningen på tur- och returresan är
\Delta V=\frac{\Delta E}{\eta H}=\frac{2mg\Delta h}{\eta H}=0,368923\,{\rm l}\approx 0,37\,{\rm l}.
Poängsättning:
För åtminstone turresan har det förklarats antingen med ord eller genom storhetsekvationer att energi omvandlas till potentialenergi och arbete som utförs av motståndskrafterna. (2 p.)
Värmevärdet har kopplats till lösningen via en storhetsekvation. (2 p.)
En storhetsekvation för den förbrukade bensinens volym har härletts. (2 p.)
Rätt svar har givits med 2 – 3 gällande siffrors noggrannhet. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Arbetet som utförs av motståndskrafterna framgår inte i lösningen, trots att det förorsakar den största delen av bensinförbrukningen.
5.2 Hur påverkas skillnaden mellan bensinförbrukningen på tur- och returresan om man på turresan kör med en högre hastighet än på returresan? 6 p.
Då man på turresan kör med en högre hastighet än returresan är arbetet som motståndskrafterna utför större på turresan än på returresan. Varvid
\Delta E=E_{\rm tur}-E_{\rm retur}=2mg\Delta h +W_{\rm tur}-W_{\rm retur}>2mg\Delta h,
alltså ökar skillnaden i energiförbrukning och samtidigt ökar skillnaden i bensinförbrukning.
Poängsättning:
Det har identifierats att arbetet som motståndskrafterna utför är större då det körs med högre hastigheter, eller det har beskrivits någon annan korrekt fysikalisk orsak för en ökning av energiförbrukningen. (2 p.)
Det har konstaterats att förbrukningen av energi eller bensin till en början redan var större under turresan. (2 p.)
Korrekt slutsats har konstaterats. (2 p.)
Typiska fel:
Endast en förklaring att bensinförbrukningen ökar när hastigheten ökar är inte tillräcklig.
En ökning av bensinförbrukningen vid högre hastigheter har motiverats med att rörelseenergin ökar.
6. Ljud på Mars 15 p.
6.1 Varför var förekomsten av ljudvågor i Mars gasatmosfär en betydande upptäckt som skakade om vetenskapsvärlden? 3 p.
En ljudvåg behöver ett medium för att framskrida. Man hade antagit att gasatmosfären på Mars antingen hade för låg densitet eller för lågt tryck eller att bådadera var för låga för att en ljudvåg skulle kunna framskrida.
Poängsättning:
Behovet av ett medium har identifierats (1 p.) och en referens har gjorts till ett lågt tryck eller densitet hos atmosfären på Mars. (2 p.)
Typiska fel:
Förklaringar där det spekulerats om liv eller uppkomsten av ljud på Mars.
6.2 Hur skiljer sig det ömsesidiga beroendet mellan ljudets hastighet och frekvens på Mars från deras beroende på jordens yta? 3 p.
Ljudets hastighet på jordens yta är (ungefärligt) konstant som funktion av frekvensen (inom hörselområdets frekvenser).
Poängsättning:
Det har konstaterats att ljudets hastighet på jorden är konstant. (3 p.)
Typiska fel:
Förklaringar där det påstås att ljudets hastighet ändrar enligt ekvationen v = \lambda f.
6.3 Vi åskådliggör skillnaden på 20 dB som observerades på Mars med ett experiment som görs på jordens yta. Hur mycket måste ljudets intensitet på jorden ökas i förhållande till den ursprungliga intensiteten om vi vill öka ljudnivån med 20 dB? 5 p.
Vi använder storhetsekvationen för ljudnivå:
L=10\,{\rm dB}\cdot\log\frac{I}{I_0},där
I_0=10^{-12}\,\frac{\rm W}{{\rm m}^2}.Nu gäller
L_1-L_2=10\,{\rm dB}\cdot\log\frac{I_1}{I_0}-10\,{\rm dB}\cdot\log\frac{I_2}{I_0}=20\,{\rm dB}.Ur det här får vi
\log\frac{I_1}{I_0}-\log\frac{I_2}{I_0}=2och vidare
\log\frac{I_1}{I_2}=2\,\Rightarrow\,\frac{I_1}{I_2}=10^2=100.Intensiteten måste alltså vara hundra gånger så stor om man vill öka ljudnivån med 20 dB.
Poängsättning:
Lösningen har motiverats med det logaritmiska beteendet av ljudnivån eller med ljudnivåns storhetsekvation (2 p.) och rätt slutresultat har givits med 1 gällande siffras noggrannhet. (3 p.) För övrig noggrannhet är avdraget 1 poäng.
6.4 Diskutera utgående från den givna informationen, hurdan upplevelsen av att lyssna på tal eller musik skulle vara på Mars i jämförelse med hurdan den skulle vara på jorden med antagandet att det skulle vara möjligt att höra ljuden på Mars utan extra skyddsarrangemang. 4 p.
På Mars skulle alla ljud höras (20 dB) mera dämpade. Dessutom skulle högre toner (över 400 Hz) höras tidigare än lägre toner, eftersom de högre tonerna framskrider ungefär 4 % fortare. Därmed skulle tal eller musik låta otydligt.
Poängsättning:
Det har identifierats att ljudet hörs mera dämpat (2 p.) och att tal eller musik blir otydligt på grund ljudets olika framskridningshastigher. (2 p.)
Typiska fel:
Det har svarats att ljudnivån är 20 dB lägre.
7. Deuterium-plasma 15 p.
Vid hög temperatur är materian i ett fjärde tillstånd, alltså som ett plasma, vilket kan beskrivas som en joniserad gas. I plasmafasen rör sig atomernas kärnor och elektroner fritt från varandra. Ett plasma kan styras med el- och magnetfält.
Deuterium är tungt väte i vars kärna det finns en proton och en neutron. Ett deuteriumplasma innehåller därmed elektroner och deuteriumkärnor, alltså deuteroner.
7.1 I en anordning som innehåller ett plasma finns till en början ett homogent magnetfält men inget elektriskt fält. Begynnelsehastigheterna för en deuteron och en elektron är vinkelräta mot magnetfältet. Hur rör sig deuteronen och elektronen i magnetfältet? På vilka två sätt skiljer sig deras rörelser från varandra? 6 p.
I ett homogent magnetfält rör sig deuteronen och elektronen i cirkelbanor med konstant fart bestämd av begynnelsehastigheten, och i ett plan vinkelrätt mot magnetfältet. På grund av skillnaden i massorna skulle radierna på cirkelbanorna vara olika, och på grund av laddningarnas motsatta förtecken skulle omloppsriktningarna vara motsatta.
Poängsättning:
I lösningen har det påpekats att partiklarna rör sig i cirkelbanor (2 p.), att banorna har olika radier (2 p.) och att cirkelbanornas omloppsriktningar är motsatta. (2 p.)
Typiskt fel:
Endast utgångsläget har undersökts i vilket fall förklaringen slutar med att partikeln rör sig linjärt eller med böjd bana.
7.2 I anordningen som innehåller ett plasma finns ett homogent magnetfält. Ett homogent elektriskt fält läggs till så att det har samma riktning som magnetfältet. Deuteronens begynnelsehastighet är vinkelrät mot magnetfältet. Förklara varför deuteronen rör sig i enlighet med den skruvlinjeformade banan i bild efter att det elektriska fältet kopplats på. 5 p.
Eftersom deuteronen är en laddad partikel styrs dess rörelse av el- och magnetfälten. Rörelsen i cirkelbana orsakad av magnetfältet hålls riktad vinkelrätt mot fältet. Det elektriska fältet ger upphov till en kraft \vec{F} = q\vec{E} = +e\vec{E} som orsakar en accelererad rörelse i det elektriska fältets riktning. När magnetfältet och det elektriska fältet verkar tillsammans ser vi den skruvlinjeliknande helix-rörelsen som visas i bilden.
Poängsättning:
Det har identifierats att magnetfältet orsakar rörelsen i cirkelbana (2 p.) och att det elektriska fältet orsakar en rätlinjig rörelse. (2 p.) som är accelererad. (1 p.)
7.3 Bränslet i en fusionsreaktor är i form av ett plasma. Varför används just el- och magnetfält för att styra plasmat i en fusionsreaktor? Varför försöker man hålla plasmat tätt? 4 p.
Byggmaterialen i en fusionsreaktor skulle smälta om partiklarna i det heta (106...108 K) plasmat vidrörde dem. Därför går det inte att hålla plasmat inneslutet med fasta konstruktioner. Beröringen undviks genom att plasmat styrs med el- och magnetfält.
Om byggmaterialen blandades med plasmat skulle det även komma orenheter i det, vilket skulle hindra fusionsreaktionerna.
En fusionsreaktion kräver att de positivt laddade väteisotopernas kärnor överskrider Coulombbarriären för att fusioneras. Då plasmats densitet ökar kommer sannolikheten för fusionsreaktioner att öka. Fusionsreaktorns verkningsgrad beror på produkten av plasmats densitet, inneslutningstiden och temperaturen (Lawsons kriterium).
Poängsättning:
Det har nämnts att plasmat har en hög temperatur och i samband med det att väggmaterialen smälter. (2 p.)
En större densitet har kopplats till en större sannolikhet för att reaktioner ska ske. (2 p.)
8. Jodbehandling 15 p.
8.1 Skriv ut sönderfallsreaktionen för I-131. 3 p.
Poängsättning:
Sönderfallsreaktionen är korrekt. (3 p.)
Typiska fel:
Neutrinon saknas eller fel grundämne används som reaktionsprodukt.
8.2 Som följd av sönderfallet uppstår även gammastrålning när dotternuklidens excitationstillstånd återgår till grundtillståndet. Bestäm gammastrålningens halveringstjocklek. Jämför lämpligheten av den beta- och gammastrålning som uppstår vid jodbehandling när det gäller att förstöra cancercellerna. 6 p.
Enligt absorptionslagen I(x)=I_0e^{-\mu x} minskar gammastrålningens intensitet i vävnaden till hälften på sträckan
x=\frac{\ln(I_0/I)}{\mu}=\frac{\ln 2}{\rm 0,11\frac{1}{\rm cm}}\approx 6\,{\rm cm}.Hälften av gammastrålningen absorberas på den här sträckan men hälften fortsätter en längre väg genom vävnaden och till och med utanför kroppen. Gammastrålningens energi absorberas på ett stort område i kroppen, vilket gör att den inte är effektiv vid förstörandet av cancersvulsten.
Enligt materialet är räckvidden i vävnaden för elektronerna som uppstår vid betasönderfall ungefär en millimeter, vilket gör att deras rörelseenergi absorberas lokalt i vävnaden. Därmed förstör betastrålningen från radiojod som bundits till sköldkörtelvävnaden effektivt cancerceller i den närbelägna vävnaden.
Poängsättning:
Med 1–2 gällande siffrors noggrannhet har rätt halveringstjocklek givits. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Ur jämförelsen framkommer det att betastrålning avger sin energi lokalt (2 p.), medan gammastrålning avger energi även utanför sköldkörteln. (2 p.)
Typiska fel:
Inversen av attenueringskoefficienten har givits som halveringstjocklek.
En jämförelse har gjorts endast utgående från energierna eller endast mellanstrålningarnas räckvidder.
8.3 Patienten får dricka en vätska som innehåller I-131 med aktiviteten 6,5 GBq. 20 % av joden binds till den kvarvarande sköldkörtelvävnaden och resten sprids runt i övriga delar av kroppen. Hur många fulla dygn måste man vänta innan patienten kan skrivas ut och skickas hem efter att den radioaktiva joden har getts? 6 p.
Av ursprungsdosen, A_0=6,5\,{\rm GBq} binds en del, x=0,2 , till sköldkörtelvävnaden där radioaktiviteten minskar i enlighet med sönderfallslagen så att den fysikaliska halveringstiden är T_{\rm fys}=8,02\,{\rm d}. Den andel, 1-x=0,8 , som finns i övriga delar av kroppen kommer att ha en effektiv halveringstid på
\frac{1}{T_{\rm ef}}=\frac{1}{8,02\,{\rm d}}+\frac{1}{1\,{\rm d}}=1,1247\,\frac{1}{\rm d}\,\Rightarrow\,T_{\rm ef}=0,8891\,{\rm d}.
Jodens radioaktivitet i både sköldkörteln och övriga delar av kroppen kommer att minska i enlighet med sönderfallslagen A=A_0e^{\lambda t}=A_0e^{-(\ln 2)t/T_{1/2}} . Radioaktiviteten hos patientens kropp är därmed A=xA_0e^{-(\ln 2)t/T_{\rm fys}}+(1-x)e^{-(\ln 2)t/T_{\rm ef}}.
Det här kan lösas exempelvis genom en grafisk framställning av minskningen i radioaktiviteten hos patientens kropp:
Patienten kan skrivas ut då fem dygn förflutit sedan radiojoden administrerats.
Poängsättning:
Den effektiva halveringstiden har bestämts korrekt. (2 p.)
Andelarna jod i sköldkörteln och i resten av kroppen har behandlats korrekt. (2 p.)
Rätt slutresultat har givits som hela dygn (2 p.) Ifall att svaret har givits som decimaltal eller att avrundningen har gjorts nedåt är avdraget 1 poäng.
Typiska fel:
21 dygn; endast fysikaliska halveringstiden har använts.
2,2 dygn: den effektiva halveringstiden har använts, men andelen jod som blir kvar i sköldkörteln har inte beaktats.
Del 3: 20-poängsuppgifter
9. En tramphjulskran 20 p.
9.1 Förklara med hjälp av en lämplig figur vilka krafter som orsakar kraftmoment med avseende på valsens och tramphjulets gemensamma axel. Vid vilken position på tramphjulet måste en människa ställa sig för att lasten ska börja stiga? Ge ditt svar med hjälp av vinkeln α mellan den lodräta riktningen och radien för tramphjulet som går via människans fötter. 12 p.
Radierna för kranens tramphjul och valsen är R = 2,0 m respektive r = 0,17 m, lastens massa är ml = 420 kg och personens massa är mp = 81 kg. Tyngdaccelerationen är g = 9,81 m/s2, lastens tyngdkraft Gl = mlg = 4120 N och personens tyngdkraft Gp = mpg = 794,6 N.
I den tillhörande bilden är F repets spännkraft. Då lasten just är på väg att röra sig har stödkraften som underlaget påverkar lasten med minskat till noll och repets spännkraft motverkar lastens tyngdkraft enligt bilden till vänster. Vi väljer uppåt som den positiva riktningen och får jämviktsvillkoret i formen F - Gl = 0. Siis F = Gl = 4120 N.
Sedan undersöker vi tramphjulet, personen och valsen i kombination och väljer i den högra bilden medurs som rotationsriktning. I kombinationen verkar kraftmomentet från personens tyngdkraft GpR sin α och kraftmomentet på valsen från repets spännkraft -Fr. De motverkar varandra, alltså är momentets jämviktsvillkor GpR sin α -Fr = 0.
Därmed är \sin\alpha=Fr/G_\rm{p}R=0,4407, alltså α = 26,15°. Lasten börjar stiga då α > 26°.
Poängsättning:
En figur relaterad till tramphjulet har presenterats så att det i figuren syns de korrekta krafterna som orsakar kraftmomenten. (2 p.)
Det har motiverats att F = Gl. (2 p.)
En storhetsekvation har skrivits för kraftmomenten med de korrekta momentarmarna (4 p.) och momentets jämviktsvillkor har fastställts antingen som storhetsekvation eller med ord. (2 p.)
Med 2 – 3 gällande siffrors noggrannhet har rätt svar givits för vinkeln. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
9.2 Då människan börjar promenera roterar tramphjulet jämnt med 2,0 varv i minuten. Bestäm lastens hastighet och kranens effekt. 4 p.
Tramphjulets och valsens rotationshastigheter är n = 2,0 1/min , alltså är valsens rotationstid T =1/n. Lastens hastighet är lika hög som hastigheten hos repet som viras runt valsen, och den är i sin tur lika hög som hastigheten hos en punkt på valsens periferi, alltså v = 2π r/T = 2 π rn = 35,60 mm/s ≈ 36 mm/s.
Kranens effekt kan bestämmas som effekten av den spännkraft från repet som påverkar lasten. Eftersom lasten inte accelererar gäller jämviktsvillkoret från deluppgift 9.1 även här. Den efterfrågade effekten är P = Fv = Glv = 146,7 W ≈ 150 W.
Poängsättning:
Med 2 – 3 gällande siffrors noggrannhet har rätt svar givits för hastigheten (2 p.) och effekten. (2 p.) För övrig noggrannhet, eller om något fel med en faktor två har gjorts, är avdraget 1 poäng.
9.3 Med tramphjulskranar i antikens Rom lyftes med människokraft laster som vägde flera ton, exempelvis när Colosseum eller Pantheon byggdes. På vilka olika sätt kan kranen i bild utvecklas för att det ska bli möjligt att lyfta tyngre föremål? 4 p.
På ett tillräckligt brett tramphjul ryms på en gång flera personer bredvid varandra. Anordningens utväxling kan ökas genom att man ökar på förhållandet mellan tramphjulets och valsens diametrar eller genom att öka antalet block.
Poängsättning, de två bästa beskrivna förslagen bedöms:
Det har föreslagits en ökning av tramphjulets diameter eller en minskning av valsens diameter med en fördel i momentarmen som motivering. (2 p.)
Det har föreslagits en ökning av människans massa eller av antalet människor, eller installation av ett till tramphjul för att skapa en större kraft. (2 p.)
Det har föreslagits att ett block kan användas eller att blockens antal ökas. (2 p) Blocket får inte vara felbeskrivet.
Typiska fel:
Det har föreslagits att tramphjulet ska förstoras utan att beskriva om det betyder en ökning av diametern eller en breddning av hjulet.
10. Dykning 20 p.
10.1 Bestäm trycket som påverkar dykarens kropp vid ett djup på 65 meter om lufttrycket vid havsytan är 101,3 kPa. 3 p.
Trycket som verkar på dykarens kropp är summan av det hydrostatiska trycket och lufttrycket:
p = ph + p0 = ρgh + p0
där ρ = 1,0 ⋅ 103 kg/m3 är vattnets densitet, g = 9,81 m/s2 är tyngdaccelerationen, h är djupet under havsytan och p0 = 101,3 kPa är lufttrycket vid havsytan.
Det sammanlagda trycket vid 65 meters djup är
p = ρgh + p0 = 1,0 ⋅ 103 kg/m3⋅ 9,81 m/s2 ⋅ 65 m + 101,3 kPa = 738,950 kPa ≈ 740 kPa.
Poängsättning:
En storhetsekvation har givits för det hydrostatiska trycket (1 p.) och med hjälp av den har trycket givits med 2–3 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
Trycket vid vattenyta har inte beaktats.
10.2 Vid ett exceptionellt långvarigt dyk på 65 meters djup har en dykare andats vanlig luft under tryck som innehåller 78 % kväve. Dykaren stiger för snabbt till ytan så att inget överlopps kväve hinner lämna dykarens kropp. Bestäm i milliliter den totala volymen av bubblorna som skapats av överloppskvävet i dykarens blod. Volymen av dykarens blod är 5,0 liter och dess temperatur är 37 °C. Lufttrycket vid havsytan är 101,3 kPa. Proportionalitetskonstanten i Henrys lag är 6,0 μmol/(m3 · Pa) för kväve. 7 p.
Enligt Henrys lag är koncentrationen av kvävet som löst sig i blodet direkt proportionell mot kvävets partialtryck, alltså c = HspN₂, där Hs = 6,0 μmol/m3 ⋅ Pa är en proportionalitetskonstant och pN₂ = 0,78⋅ p är kvävets partialtryck då totala trycket är p. Substansmängden kan beräknas genom att multiplicera koncentrationen med lösningens volym, n = cV.
Substansmängden av kvävet som löst sig i blodet på 65 meters djup är
n1 = HspN₂V0 = 0,78 ⋅ (ph + p0)V0,
där V0 =5,0 l = 0,005 m3 är blodets volym, ph är det hydrostatiska trycket och p0 = 101,3 kPa är lufttrycket vid havsytan.
Substansmängden för kvävet som löst sig i blodet vid havsytan är
n2 = HspN₂V0 = Hs ⋅ 0,78 ⋅ p0V0,
varvid substansmängden för överloppskvävet är
n = n1 - n2 = Hs ⋅ 0,78 ⋅ (ph + p0 - po)V0 = Hs ⋅ 0,78 ⋅ phV0.
Kväve är en inert gas och beter sig vid tillräckligt låga tryck som en ideal gas. Därför kan volymen av överloppskvävet beräknas med hjälp av tillståndsekvationen för en ideal gas, pV = nRT.
Volymen av överloppskvävet är
V=\frac{nRT}{p}=\frac{1}{p_0}H_s\cdot 0,78\cdot p_hV_0RT,där R = 8,314510 Pa m3 / mol ⋅ K och T = 37°C = 273,15 K + 37°C = 310,15 K är temperaturen.
Eftersom det hydrostatiska trycket är ph = ρgh, där ρ =% 1,0 ⋅ 103 kg/m3 är vattnets densitet, g = 9,81 m/s2 är tyngdaccelerationen och h = 65 m är djupet under havsytan får vi
V=\frac{1}{p_0}H_s\cdot 0,78\cdot \rho g hV_0RT =\frac{1}{101300\,{\rm Pa}}\cdot6,0\cdot 10^{-6}\frac{\rm mol}{{\rm m}^3{\rm Pa}}\cdot 0,78\cdot 1,0\cdot 10^3\,\frac{\rm kg}{{\rm m}^3}\cdot 9,81\,\frac{m}{{\rm s}^2}\cdot 65\,{\rm m}\cdot 0,005\,{\rm m}^3 \cdot 8,314510\,\frac{{\rm Pa}\,{\rm m}^3}{{\rm mol\,K}}\cdot 310,15\,{\rm K}=0,00037984\,{\rm m}^3\approx 380\,{\rm ml} Den totala volymen av kvävebubblorna som uppstår i blodet är alltså ungefär 380 ml.
Poängsättning:
Ur lösningen framgår det att substansmängdernas skillnad beräknas. (2 p.)
Det har givits en storhetsekvation för kvävets substansmängd (1 p.) och påpekats att kvävet beter sig som en ideal gas. (2 p.)
Med 2–3 gällande siffrors noggrannhet har rätt svar givits. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
10.3 Bestäm med hjälp av tabell och någon anpassning gjord i en grafisk presentation den maximala tid som en dykare kan vistas på 10 meters djup utan att hen måste göra ett särskilt dekompressionsstopp under uppstigningen. 4 p.
Till mätdata i tabell 10.B kan vi anpassa en potensfunktion i ett djup-tid-koordinatsystem.
Den maximala tiden vid olika djup kan sedan bestämmas antingen genom att extrapolera eller genom att använda anpassningens ekvation:
f(10) = 19870 ⋅ 10-2,026 min = 187,154 ≈ 190 min.
På djupet 10 m är dykets maximala tid 190 min.
(Beroende på anpassningen och beräkningsprogrammet godkänns slutresultat inom intervallet 160 min … 210 min.)
Poängsättning:
En grafisk presentation har gjorts ur vilken det syns en lämplig anpassning som är gjord för hela punktmängden. (2 p.) Potensfunktionen är en ger anpassning till de här mätpunkterna men genom att använda den kan man få poängen för ett korrekt svar i den här deluppgiften.
Med 2–3 gällande siffrors noggrannhet har rätt svar erhållits inom intervallet 160 – 210 min utgående från anpassningen. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
10.4 Bestäm med hjälp av tabell och en anpassning gjord i en grafisk presentation halveringstiden för överloppskväve i människokroppen, alltså tiden det tar för hälften av överloppskvävet att lämna dykarens kropp. 6 p.
Tabell 10.C presenterar den maximala tiden vid omdykning som funktion av pauslängden mellan dyken. Omdykets varaktighet kan vara längre efter en mera långvarig paus eftersom en större mängd kväve då har hunnit lämna kroppen.
Hastigheten med vilken överloppskvävet som löst sig i kroppen under det första dyket försvinner ur kroppen kan bedömas genom att jämföra hur mycket omdykets maximala tid förkortas vid olika längder på pauserna mellan dyken. Förkortningen kan beräknas som differensen mellan det ursprungliga dykets maximala tid, tu = 35 min, och omdykets maximala tid to: t = tu - to.
Med hjälp av tabellberäkning kan vi beräkna förkortningen i den maximala tiden för varje omdyk, varefter förkortningen kan ritas i en graf som funktion av pauslängden. Förkortningen, och därmed även minskningen av överloppskvävet, är exponentiell, alltså kan halveringstiden av överloppskvävet bedömas genom att anpassa en exponentialfunktion till punktmängden.
Anpassningens ekvation är till formen lik den allmänna sönderfallslagen, N = N0e-λt, ur vilken halveringstiden kan beräknas med hjälp av sönderfallskonstanten:
T_{1/2}=\frac{\ln 2}{\lambda}=\frac{\ln 2}{0,005464\,\frac{1}{\rm min}}=126,857\,{\rm min}\approx 130\,{\rm min},alltså är halveringstiden för överloppskvävet ungefär 130 min.
Poängsättning:
Förkortningen av dyktiden har beräknats eller använts i en graf. (2 p.)
En grafisk presentation har gjorts och en exponentiell anpassning har gjorts till den. (2 p.)
Med 2–3 gällande siffrors noggrannhet har det givits ett svar inom intervallet 100 – 150 som erhållits med en exponentiell anpassning. (2 p.) För övrig noggrannhet är avdraget 1 poäng.
Typiska fel:
En exponentialfunktion har anpassats till ursprungliga data.
Något annat än en exponentialfunktion har använts som anpassning.
11. En kylväska 20 p.
11.1 En kylväska som är kopplad till en inverter fungerar ännu med en liten effekt efter att bilen stannat. Hur lång tid tar det innan laddningsnivån för bilens ackumulator sjunker från full till 20 % då kylväskan fungerar kontinuerligt med en medeleffekt på 35 watt? Inverterns verkningsgrad är 87 % och ackumulatorn har en kapacitet på 60 Ah. 4 p.
Ackumulator i en bil har spänningen 12 V, alltså är ackumulatorns kapacitet given i wattimmar E = It ⋅ U = 60 Ah ⋅ 12 V = 720 Wh. Den sammanlagda effekten för ackumulatorn och invertern är P = P0 / η = 35 W / 0,87 = 40,2 W. Ackumulatorns laddningsnivå sjunker med 20 % på tiden t = (0,8 ⋅ E) / P = 14,32 h ≈ 14 h.
Poängsättning:
Med 2–3 gällande siffrors noggrannhet har ett svar givits inom intervallet 14 h 0 min – 14 h 20 min. (4 p.) För övrig noggrannhet eller felaktig omvandling av timmar till minuter är avdraget 1 poäng.
11.2 Då kylväskan går på full effekt uppmäts storleken på spänningen och den elektriska strömmen som går till den från invertern (). Bestäm kylväskans genomsnittliga effektförbrukning. 10 p.
Uppgiften kan lösas på flera olika sätt. I tabellen nedan beskrivs i stora drag skedena i fyra olika lösningsmetoder och poängen som ges för dem.
Som genomsnittlig effekt får vi ungefär 75 W.
| Metod | Graf + medeltal | Graf + grafisk integrering | Tabellberäkning, medeltal eller pulsförhållande | Tabellberäkning, I2R | Poäng |
|---|---|---|---|---|---|
| Skede 1 | Den momentana effekten bestäms, med motiveringar, genom att multiplicera tabellens kolumner sinsemellan | Den momentana effekten bestäms, med motiveringar, genom att multiplicera tabellens kolumner sinsemellan | Den momentana effekten bestäms, med motiveringar, genom att multiplicera tabellens kolumner sinsemellan | Resistansen bestäms, med motiveringar, och storheten I2 beräknas | 4 |
| Skede 2 | Val av intervall med korrekt längd från grafen för att bestämma de olika värdena | Val av intervall med korrekt längd från grafen för att bestämma de olika värdena | Val av korrekt intervall från tabellen ELLER Bestämning av korrekt pulsförhållande | Val av intervall med korrekt längd från grafen för att bestämma de olika värdena | 2 |
| Skede 3 | Bestämning av medelvärde, med motivering | Grafisk integrering och division med korrekt tidsintervall | Beräkning av medelvärde med motivering ELLER Beräkning med pulsförhållande | Beräkning av medelvärde ur kvadrerade värden, med motivering | 2 |
| Skede 4 | Slutresultat | Slutresultat | Slutresultat | Slutresultat | 2 |
Typiska fel:
För att bestämma medelvärdet har hela området har valts i stället för något antal fulla perioder.
Tiden då effekten är noll har inte beaktats.
Formlerna för sinusformad växelspänning har använts.
11.3 Funktionen hos billiga kylväskor grundar sig vanligen på Peltierelement. Information om anordningen finns i material och . Bedöm utgående från materialet vilka faktorer som försämrar kylningseffekten hos kylväskor som fungerar med Peltierelement. 6 p.
Då den elektriska strömmen ökar kommer spillvärmeproduktionen att öka snabbare än kylningseffekten. Temperaturskillnaderna i elementet kommer åt att jämnas ut rätt enkelt eftersom de varma och kalla sidorna är mycket nära varandra. Dessutom finns det ett material med god värmeledningsförmåga mellan de varma och de kalla sidorna (medan materialet på utsidorna är sämre på att leda värme).
Poängsättning:
Spillvärme har identifierats som en faktor som minskar på kylningseffekten (1 p.) och det har berättats att spillvärmet ökar snabbare än kylningseffekten då strömmen ökar. (3 p.)
Värmeledning genom Peltierelementet har identifierats som en begränsande faktor för effekten. (2 p.)