Hyvän vastauksen piirteet: FI – Matematiikka, lyhyt oppimäärä
19.9.2023
Lopulliset hyvän vastauksen piirteet 9.11.2023
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.
Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.
Miten pisteytysohjeita luetaan
- Ohjeen rakenne
- Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy oikeassa sarakkeessa olevaan pistemäärään.
- Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
- Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
- Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
- Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esim. derivaatan laskeminen osittain oikein).
- Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
- Suluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
- Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
- Rivien riippuvuus toisistaan
- Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esim. laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
- Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
- Merkintä ylläolevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
- Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
- Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
- Terminologiaa
- ''Vastaus riittää'' tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
- ''Alkupisteitä'' tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
- ''maxN'' tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
- ''Vastaus vain likiarvona'' tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.
- Vastaus oikein, muttei pyydetyssä muodossa (esim. tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esim. e^1, ln (e) tai 4^0 -2 p.
- Vastaus sieventämättä muussa tehtävässä (esim. e^1, ln (e) tai 4^0 -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esim. x =2, y04, tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.
- Matemaattisesti puutteellinen merkintä (esim. puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
Kolmisarakkeisen lukuohjeet:
- Ideasarakkeesta saa pisteet, jos on ryhdytty tekemään mainittua asiaa, vaikka toteutus olisi puutteellinen.
- Lasku tai kaava toteutussarakkeessa näyttää, miltä idea oikein toteutettuna näyttää.
- Pysäytysehto: jokaiselta riviltä saatava vähintään puolet rivin pisteistä pyöristettynä alaspäin, jotta voi jatkaa.
- Jos pysäytysehto ei toteudu, eli seuraavien rivien pisteitä on vielä jaossa, on seuraavilta riveiltä saatavissa kaikki pisteet, joissa ei ole eksplisiittistä estettä sille, miksi niitä ei voisi saada.
A-osa
1. Funktiot ja lukujonot 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 2 p.
- 6 (2 p.)
1.2 2 p.
- 4 (2 p.)
- +-4 (1 p.)
1.3 2 p.
- x^3 +x^2 (2 p.)
- x^3 +x^2 +4 (1 p.)
1.4 2 p.
- 6 x^2 +12 (2 p.)
1.5 2 p.
- 13 (2 p.)
1.6 2 p.
- 11 (1 p.)
- 15 (2 p.)
1.3 virheellinen, mutta oikeansuuntainen vastaus (1 p.) x^3 +x^2 +4.
1.6 virheellinen, mutta oikeansuuntainen vastaus (1 p.) 11.
2. Vaatekaupassa 12 p.
Farkkujen alkuperäinen hinta on 56,00 euroa ja alennusmyynnissä hintaa alennetaan 30 %. Mikä on alennettu hinta? (4 p.)
Takin alkuperäinen hinta on 79,00 euroa ja alennettu hinta 55,30 euroa. Mikä on alennusprosentti? (4 p.)
Vaatteiden arvonlisäverokanta on 24 %. Kuinka monta euroa paidan 45,00 euron myyntihinnasta on arvonlisäveroa? (4 p.)
| Kerroin 0,7 TAI 0,3 *56 =16,80 | 2 p. |
| Alennettu hinta on 0,7 *56,00 =39,20 (euroa) TAI 56,00 -16,80 =39,20 (euroa). Tämä tarkkuus vaaditaan. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Vastaus 39,2. | –0 p. |
| Uusi hinta on 55,30 /79 =0,7 =70 prosenttia alkuperäisestä hinnasta TAI 79,00 -55,30 =23,70 (euroa). | 2 p. |
| Alennus on siis 30 prosenttia TAI 22,70 /79 =0,30 =30 % = 30 %. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Vastaus ja tarkistuslasku. | 2 p. |
| Pelkkä vastaus. | 0 p. |
| ALV on 24 prosenttia verottomasta hinnasta. Tämä voi käydä ilmi myös kertoimen 1,24 oikean suuntaisesta tarkista, tuleeko yhteen ja korjaa samanlaiseksi kuin t. 1. käytöstä. | (1 p.) |
| Yhtälö 1,24 x =45 verottomalle hinnalle x. | 1 p. |
| Saadaan X =45 /1,24 ~~36,29 (euroa). | 1 p. |
| ALV:n määrä on siis 45,00 -36,29 ~~8,71 (euroa). | 1 p. |
| TAI | |
| 45 /1,24 *0,24 ~~8,71 (euroa). | 4 p. |
| Osatehtäväkohtaiset erillisohjeet | 1 p. |
| Laskettu vain 0,24 *45 tai 0,76 *45. | 0 p. |
| Tässä osatehtävässä vaaditaan sentin tarkkuus. |
| Tehtäväkohtaiset erillisohjeet | |
| Yksittäisissä osatehtävissä ei vaadita selityksiä. Jos koko tehtävän missään osatehtävässä ei ole yhtään selitystä tai edes sanaa, niin selitysten puutteen vuoksi: | max 11 p. |
| Yleisvähennys huonoista merkinnöistä: Jos tehtävässä esiintyy muotoa 56 -30 % =39,20 olevia tai vastaavia yhtälöitä, niin | –1 p. |
3. Tuntemattomia muuttujia 12 p.
Kuvassa on suora y = ax + b, jonka kertoimet a ja b ovat kokonaislukuja. Päättele kuvaajan perusteella kertoimien arvot ja perustele, miten päädyit ratkaisuun. (4 p.)
Ratkaise p murtolukuna yhtälöstä \displaystyle\Big(\frac35+\frac34\Big)\cdot p=\frac35. (2 p.)
Ratkaise q murtolukuna yhtälöstä \displaystyle\Big(\frac13-\frac12\Big):q=\frac12. (2 p.)
Ratkaise x yhtälöstä \displaystyle\frac{4n^{2^3} (n^2)^3}{2n}\cdot x=8n^{10}. (4 p.)
| Oikea idea kulmakertoimen laskemiseksi: Suora kulkee pisteiden (0, -2) ja (1, 1) kautta, kulmakerroin on siis k=\frac{1-(-2)}{1-0} TAI vastaava sanallinen selitys. | 1 p. |
| \bullet\, a=k=3. | 1 p. |
| Oikea idea kertoimesta b (suoran ja y-akselin leikkauspisteen (0,-2) y-koordinaatti). | 1 p. |
| \bullet\, b=-2. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Vastaukseksi riittää kertoimet, suoran yhtälöä ei tarvita. | |
| Arvattu suoran yhtälö ja testattu arvaus kahdessa pisteessä. | 3 p. |
| Yhtälö (3/5 +3/4) *p =3/5 sievenee muotoon (1/5 +1/4) *p =1/5 TAI 27/20 *p =3/5 TAI 27/20 *p =12/20. | 1 p. |
| Siispä [(4 +5) /20] *p =1/5, joten p =4/9 (vastaus annettava murtolukuna). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pieni laskuvirhe, joka ei olennaisesti helpota tehtävää. | –1 p. |
| Vastaus ja tarkistuslasku. | 1 p. |
| Yhtälö (1/3 +1/2) /q =1/2 sievenee muotoon -1/6 /q =1/2. | 1 p. |
| Siispä q=-1/6 *2 =-1/3 (vastaus annettava murtolukuna). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Jos ratkaisussa on vain yksi virhe, eikä tehtävä helpotu oleellisesti, niin | 1 p. |
| Vastaus ja tarkistuslasku. | 1 p. |
| 4 n^2^3 *(n^2)^3 =4 n^8 *n^6. | 1 p. |
| Lauseke (4 n^2^3 *(n^2)^3) /(2 n) *x on sievennetty muotoon 2 n^13 x TAI nimittäjässä oleva n on poistettu oikein. | 1 p. |
| Ratkaistu muuttuja x alkuperäisestä lausekkeesta tai muokatusta (mahdollisesti virheellisestä) lausekkeesta, esimerkiksi x =(8 n^10) /(2n ^13). | 1 p. |
| Siispä x =4 n^(10 -13) =4 n^(-3) tai 4/n^3. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Muuttujan n potensseissa virhe n^2^3 =n^6 tai muu vähäinen virhe. | max 3 p. |
| Muuttujan x ratkaisemisessa virhe x =8 n^10 -2 n^13. | max 2 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Jos osatehtävien 3.2 ja 3.3 välivaiheissa on käytetty likiarvoja tai desimaaliluku on muutettu murtoluvuksi perustelematta tai vastaus on jätetty supistamatta, niin koko tehtävästä | –1 p. |
4. Pythagoraan kolmikot 12 p.
Positiiviset kokonaisluvut a, b ja c muodostavat Pythagoraan kolmikon, jos a^2 +b^2 =c^2.
Näitä kolmikoita voidaan muodostaa seuraavasti. Olkoot m ja n positiivisia kokonaislukuja, joille m > n. Tällöin luvut a =m^2 -n^2, b =2 mn ja c =m^2 +n^2 muodostavat Pythagoraan kolmikon.
Muodosta yllä esitetyllä tavalla jokin Pythagoraan kolmikko. (3 p.)
Anna esimerkki kolmesta positiivisesta kokonaisluvusta, jotka eivät muodosta Pythagoraan kolmikkoa. (3 p.)
Määritä luvut m ja n silloin, kun Pythagoraan kolmikkona ovat luvut a =15, b =8 ja c =17. (3 p.)
Perustele, että jos a, b ja c on muodostettu lukujen m ja n avulla kuten tehtävän alkutekstissä, niin a^2 +b^2 =c^2. (3 p.)
| Sijoitettu lausekkeisiin m^2 -n^2, 2mn ja m^2 +n^2 konkreettiset positiiviset kokonaisluvut m ja n, joille m > n. | 1 p. |
| Laskettu lausekkeiden arvot. | 1 p. |
| Esitetty selvästi laskut, joissa näkyy eksplisiittisesti muuttujien a, b, c, m ja n lukuarvot (m=\text{luku}, n=\text{luku}, jne.). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Annettu Pythagoraan kolmikko käyttämättä annettua menetelmää. | +0 p. |
| Muissa osatehtävissä annettu m =4 ja n =1, josta saatu a =15, b =8, c =17, ilman linkitystä osatehtävään 4.1. Tämän osatehtävän pisteisiin | +0 p. |
| Annettu positiiviset kokonaisluvut (a, b ja c), jotka eivät muodosta Pythagoraan kolmikkoa. | 1 p. |
| ylläolevista riveistä riippumaton piste Tehty sijoitukset a^2 +b^2 ja c². | 1 p. |
| Laskettu arvot ja todettu, että a^2 +b^2 !=c^2. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kolmannella rivillä riittää todeta epäyhtälö ilman laskuja, jos luvut on valittu niin, että a,b >= c. tai epäyhtälö on muusta vastaavasta syystä ilmeinen. | |
| Luvut riittävät, ei tarvitse käyttää merkintöjä a, b ja c. |
| Kun m =4 ja n =1, saadaan a =m^2 -n^2 =4^2 -1^2 =15, b =2mn =2 *4 *1 =8 ja c =4^2 +1^2 =17. | 1 p. |
| Yritetty todistaa, että muita ratkaisuja ei ole. | 1 p. |
| Todistettu, että muita ratkaisuja ei ole (esimerkiksi annettu taulukko luvuista m, n, a, b, c kun 4 >= m > n >= 1, ja todettu, että m <= 4, koska 8 =b =2 *m *n). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pelkkä vastaus m =4 ja n =1. | 0 p. |
| TAI | |
| Eliminoitu m tai n yhtälöparista (esimerkiksi a +c =(m^2 -n^2) +(m^2 +n^2) =2 m^2 tai 17 -15 =(m^2 +n^2) -(m^2 -n^2) =2 n^2). | 1 p. |
| Sijoitettu annetut arvot (esim. 32 =2 m^2 tai 2 =2 n^2) ja ratkaistu toinen muuttujan arvo. | 1 p. |
| Sijoitettu oma saatu ratkaisu toiseen yhtälöistä ja ratkaistu toinen muuttuja TAI sijoitettu oma saatu ratkaisu kolmanteen (yhtälöparin ulkopuoliseen yhtälöön) ja ratkaistu toinen muuttuja sekä tarkistettu, että se toteuttaa ainakin toisen omista alkuperäisistä yhtälöistä. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Yhtälö m^2 =16 ratkaistu ilman +-4 välivaihetta. | –0 p. |
| TAI | |
| 8 = b = 2 *m *n, eli m *n =4 =2 *2 ja etsitty ratkaisuja positiivisten kokonaislukujen joukosta. | 1 p. |
| (Ratkaisut ovat "m =4 ja n =1" tai "m =n =2" tai "m =1 ja n =4".) | 1 p. |
| Ainoa mahdollinen ratkaisu on m =4 ja n =1 (koska m >= n). | 1 p. |
| Sijoitettu a =4^2 -1^2 =15 ja c =4^2 +1^2 =17. | 1 p. |
| Sijoitettu a^2 +b^2 =(m^2 -n^2)^2 +(2 mn)^2 tai c^2 =(m^2 +n^2)^2. | 1 p. |
| Laskettu (m^2 -n^2)^2 +(2 mn)^2 =m^4 -2 m^2n^2 +n^4 +4 m^2n^2. | 1 p. |
| Laskettu kaikki sulut auki, sievennetty ja todettu lausekkeiden yhtäsuuruus. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kokeilut lukuarvoilla. | +0 p. |
B1-osa
5. Laskettelumatka 12 p.
Lukion 32 opiskelijan ryhmä varaa laskettelumatkaa varten linja-auton, jonka kustannukset jaetaan tasan osallistujien kesken. Neljä opiskelijaa joutuu perumaan lähtönsä, jolloin jokainen osallistuja maksaa lopulta 15 euroa alkuperäistä hintaa enemmän. Kuinka paljon yhden osallistujan matka lopulta maksoi?
| Tehtävä ratkaistu päättelemällä | |
| Lasku tai selitys antaa luvun 28. | (1 p.) |
| 28 *15 =420 (euroa) TAI 15 /4 =3,75 (euroa) (Oikeat luvut 1+1, laskun suorittaminen 1 p.) | 3 p. |
| 420/4 =105 (euroa) TAI 3,75 *28 =105 (euroa). (Siirtyvä lukuarvo (420 tai 3,75), jakaja 4 tai kerroin 15, laskun suorittaminen 1+1+2). | 4 p. |
| 105 +15 = melko täsmälleen \textbf{120} euroa (Vain 120 kelpaa, vastauksessa yksikkö vaaditaan.). | 1 p. |
| Selitykset, joista käy ilmi ratkaisun koko juoni. Yksi piste jokaisen edellisen rivin 2, 3 ja 4 selityksestä. | 1+1+1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Vastaus 120 euroa ja vastauksen testaus, esimerkiksi 120 *28 =105 *32. (Arvaus tulee usein väärästä yhtälöstä.) | 5 p. |
| TAI | |
| Ratkaistu yhtälön, yhtälöryhmän tai verrannon avulla | |
| Ratkaisussa käytetyt muuttujat on selitetty, esimerkiksi linja-auton kustannukset y ja kunkin opiskelijan maksama hinta x, jos lähtijöitä on 32. | 1 p. |
| Muodostettu lineaarinen yhtälöpari tai yhtälö. | 1 p. |
| Alla olevia yhtälöparin/yhtälön pisteitä saa vain lineaarisesta tapauksesta. | |
| Luku 32 on kertoimena muuttujalle, esimerkiksi y =32 x. | 2 p. |
| Luku 28 on kertoimena muuttujalle, esimerkiksi y =28 z. | 2 p. |
| Lukua 15 on lisätty/vähennetty muuttujaan, esimerkiksi x +15. | 2 p. |
| Yhtälöparissa toinen yhtälö on oikein TAI yhtälössä toinen puoli on oikein. | 1 p. |
| Yhtälöpari tai yhtälö on oikein, esimerkiksi y =32 x ja y =28(x +15) tai 32 x =28(x +15) tai x /28 =(x +15) /32. | 1 p. |
| Päästy yhden muuttujan yhtälöön ja ratkaistu muuttujat tai muuttuja. (Yhtälöparin tapauksessa pitää ratkaista molemmat muuttujat tai selittää miksi toista ei tarvita.) | 1 p. |
| Muodostettu vastaus, esimerkiksi 105 + 15 = melko täsmälleen 120 euroa. (Vain 120 kelpaa, vastauksessa yksikkö vaaditaan.) | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Riveillä 3 ja 4 pisteisiin vaaditaan, että luvut 32 ja 28 ovat kertoimina muuttujille. Poikkeuksena tapaukset, joissa selvästi ovat sulkeet unohtuneet. Esimerkiksi 28 *15 +x, jossa unohtunut sulkeet termin 15 +x ympäriltä. Tästä annetaan riviltä 4 yksi piste ja riviltä 5 yksi piste (riviltä 5 annetaan 2 pistettä, jos 15 +x on esitetty jossakin muussa ratkaisun vaiheessa oikein). |
6. Postimerkin lisäpainama 12 p.
Karoliinien saariryhmä oli yksi Saksan keisarikunnan siirtomaista. Siirtomaan ensimmäinen postimerkkisarja valmistettiin Saksan postimerkeistä painamalla niihin teksti ''Karolinen''. Lisäpainamasta on kaksi eri tyyppiä, loiva ja jyrkkä, joiden luettelohinnat ovat 1 800 ja 180 euroa. Loivan lisäpainaman kaltevuuskulma on noin 48^{\circ} vaakatasosta mitattuna ja jyrkän lisäpainaman 56^{\circ}.
Arvioi kuvan postimerkin lisäpainaman kaltevuuskulmaa. Onko lisäpainama loivaa vai jyrkkää tyyppiä? (6 p.)
Lisäpainaman ympärille piirretään mahdollisimman pieni suorakulmio. Arvioi, kuinka monta prosenttia suorakulmio peittää postimerkin pinta-alasta. Valkoisia reunoja ei lasketa mukaan postimerkin pinta-alaan. (6 p.)
Tehtävän voi ratkaista joko sopivalla ohjelmalla tai mittaamalla lukuarvoja näytöltä. Molemmissa vaihtoehdoissa täytyy käydä ilmi ratkaisutavan välivaiheet.
| Asetettu kuva koordinaatistoon ja piirretty tekstin suuntainen suora TAI mitattu näytöltä y- ja x-suuntaiset muutokset TAI piirretty lävistäjän suuntainen suora. | 2 p. |
| Suoran suuntakulma on välillä (54^{\circ},58^{\circ}) TAI mitattujen muutosten suhde on välillä (1\mathrm{,}3; 1\mathrm{,}7) TAI lävistäjän suuntakulma on välillä (47^{\circ},51^{\circ}). | 1 p. |
| Kyseessä on jyrkän tyypin merkki. | 2 p. |
| Perustelu miten kulma on määritetty TAI 1\mathrm{,}48\approx \tan(56^{\circ}). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Tekstin suuntainen suora voi olla kaksi pistettä suoralta, kolmion sivu tai vastaava objekti. | |
| Pelkkä vastaus. | 0 p. |
| Perusteluksi riittää esimerkiksi ruudunkaappauskuva, jossa näkyy laskinohjelman antama kulman suuruus. Komentoikkunan ei tarvitse olla näkyvissä. | |
| Tehtävän voi ratkaista myös kiertämällä kuvaa siten, että teksti on vaakasuorassa. | max 6 p. |
| Piirretty sekä loivan että jyrkän tyypin kulmat, mutta ei postimerkin päälle tai muuten selvästi yhdistetty postimerkkiin: 0+1+2+1. | max 4 p. |
| Piirretty vain jyrkän tyypin kulma, mutta ei postimerkin päälle tai muuten selvästi yhdistetty postimerkkiin: 0+1+1+0. | ma 2 p. |
| Alkupiste: Asetettu kuva ohjelmistoon. |
| Piirretty kohtisuorat tekstin ympärille ja niiden leikkauspisteiden kautta suorakulmio. Määritetty tämän suorakaiteen pinta-ala. Piirretty postimerkin oranssin alueen kulmia käyttäen suorakaide. Määritetty tämän pinta-ala.
| 4 p. |
| Pinta-alojen suhde \frac{9\mathrm{,}18}{60\mathrm{,}96}\approx täsmälleen \textbf{15 %}. | 2 p. |
| TAI | |
| Postimerkin pinta-ala ilman valkoisia reunoja on laskettu. | 1 p. |
| riippumaton Tekstin ympärille on piirretty silmämääräisesti mahdollisimman pieni suorakulmio | 2 p. |
| Oman suorakulmion pinta-ala on laskettu. | 1 p. |
| Pinta-alojen suhde on laskettu. | 1 p. |
| Pinta-alojen suhde on täsmälleen 15~\%. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pinta-alojen laskeminen dokumentoitava: kuvakaappauksessa mukana komennot, laskut tai selitykset. Jos nämä puuttuvat, koko osatehtävästä (riveiltä 1 ja 3) | –1 p. |
| Pituudet ja pinta-alat voidaan ilmoittaa omissa yksiköissä. Pituuksien perusteluksi riittää toteamus "Mittasin pituudet näytöltä." | |
| Hieman virheellinen nelikulmio ja vastaus 15~\%. (Piste pois riippumattomalta riviltä: 1+1+1+1+1) | max 5 p. |
| Epätarkka suorakulmio, vastaus välillä [13,17] muttei 15: (1+1+1+1+0) | max 4 p. |
| Suorakulmion sivut vaaka- ja pystysuorat (suhde = 47 %): (1+0+1+1+0) | max 3 p. |
| Pinta-alalaskuja ei ole mitenkään dokumentoitu (ei näy edes kuvaa järkevähköstä suorakulmiosta) ja vastaus on välin [13,17] ulkopuolella, niin korkeintaan alkupiste. | |
| Alkupiste: Samaan kuvaan postimerkin kanssa on piirretty jokin nelikulmio. | 1 p. |
7. Urheilusukat 12 p.
Kilpajuoksijalla on kuusi urheilusukkaa sekaisin pienessä korissa. Kolmessa sukassa on merkki L ja kolmessa R. Juoksija ottaa korista umpimähkään kaksi sukkaa peräkkäin. Määritä todennäköisyys sille, että
ensimmäisessä sukassa on merkki L (2 p.)
molemmissa sukissa on merkki L (4 p.)
sukissa on eri merkit. (6 p.)
| (Sukista kolme on L-sukkia, joten) kysytty todennäköisyys on 3/6 =1/2. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pelkkä vastaus 1/2 tai 0,5 tai 50 % | 1 p. |
| Todennäköisyys sille, että myös toisessa sukassa on L, on 2/5. | 2 p. |
| Kerrottu omat todennäköisyydet keskenään (oikea lasku 1/2 *2/5. | 1 p. |
| Vastauksena kertolaskun tulos sievennettynä (= 2/5 =1/5). Vastaus välillä (0, 1). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pelkät laskut ja vastaus. | 3 p. |
| Todennäköisyys sille, että toisessa sukassa on R, jos ensimmäisessä on ollut L, on 3/5. | 1 p. |
| Yhdistelmän L ja R (tässä järjestyksessä) todennäköisyys on siis 1/2 *3/5 =3/10. | 2 p. |
| Todennäköisyys sille, että ensimmäinen on R ja toinen L, on sama kuin todennäköisyys sille, että ensimmäinen on L ja toinen R. | 1 p. |
| riippumaton Kysytty todennäköisyys on siis 2 *(3/10) =3/5. | 2 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Tyypillinen puumallin ratkaisu arvostellaan tämän mukaan. | max 6 p. |
| Puumallia ei ole lainkaan selitetty (esimerkiksi merkitty, mitkä tapaukset vastaavat L- ja mitkä R-sukkia), niin selitysten puutteesta | –1 p. |
| Toisen sukan todennäköisyys väärin (esim. 3/6): (0+2+1+2) | max 5 p. |
| Pelkkä lasku 1/2 *3/5 =3/10 vailla selityksiä tai jatkoa: (0+2+0+0). | max 2 p. |
| TAI | |
| Vastatapahtumassa molemmat sukat samaa tyyppiä. | 2 p. |
| Tämän todennäköisyys on 1/5 +1/5 =2/5. | 2 p. |
| riippumaton Kysytty todennäköisyys on siis 1 -2/5 =3/5. | 2 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Vastatapahtumassa vain toinen tapaus (1+1+1). | max 3 p. |
| TAI | |
| Koska ensimmäinen sukka voi olla kumpi tahansa ja toisen täytyy olla erilainen, niin riittää tarkastella toisen sukan todennäköisyyttä. | 4 p. |
| riippumaton Kysytty todennäköisyys on 3/5. | 2 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Vain 6/6 *3/5 =3/5 TAI 1 *3/5 =3/5 ilman selityksiä (1+2). | 3 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Vastaukset voi ilmoittaa desimaalilukuina, prosentteina tai murtolukuina. |
8. Polynomifunktio 12 p.
Olkoon p(x) =x^4 -4 x^3 -8 x^2 +48 x.
Laske derivaatta p’(x) ja ratkaise derivaatan nollakohdat. (4 p.)
Millä väleillä funktio p on kasvava? (4 p.)
Määritä funktion p pienin arvo. Missä kohdassa se saavutetaan? (4 p.)
| Laskettu derivaatta p’(x) ja saadaan 3. asteen polynomi TAI vähintään kaksi neljästä polynomin p(x) termistä on derivoitu oikein TAI ratkaisusta ilmenee, että ohjelmistolla on käytetty oikeaa komentoa. | 1 p. |
| Derivaattafunktio p’(x) =4 x^3 -12 x^2 -16 x +48 on oikein. | 1 p. |
| Ratkaistaan omasta derivaattafunktiosta, joka on polynomi, yksi nollakohta oikein. | 1 p. |
| riippumaton Ratkaistaan kaikki nollakohdat oikein omasta derivaattafunktiosta, joka on kolmannen asteen polynomi TAI saadaan nollakohdiksi -2 2 ja 3 (esimerkiksi kuvasta katsomalla). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Derivaattafunktion nollakohdat voi ratkaista Ratkaise/Solve-komennolla. | |
| Lasketaan p:n nollakohdat. | +0 p. |
| Nollakohdat annettu muodossa (-2, 0), (2, 0) ja (3, 0) | –0 p. |
| Tehdään kulkukaavio omilla derivaatan nollakohdilla, vaaditaan derivaattafunktion arvojen laskeminen testipisteissä ja kaikkien nollakohtien mukanaolo. TAI Lasketaan (ohjelmistolla) funktion p ääriarvokohdat tai derivaatan nollakohdat ja yhdistetään tieto funktion p tai derivaatan p' kuvaajaan. | 2 p. |
| riippumaton Polynomi on kasvava, kun -2\leq x\leq 2 tai x\geq 3 (Vain tämä vastaus kelpaa). | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Hyväksytään vastauksiksi välit, joissa päätepisteet eivät ole mukana. | –0 p. |
| Oikea kulkukaavio on - | + | - | + nollakohdilla -2, 2 ja 3. |
| Tarkastellaan funktion arvoja kohdissa, jotka oman tarkastelun kuten kulkukaavion perusteella ovat funktion p lokaaleja minimikohtia tai derivaatan nollakohtia. | 1 p. |
| Sijoitetaan omat minimikohdat funktion p lausekkeeseen ja lasketaan funktion p arvot niissä. | 1 p. |
| Koska p(-2) =-80 ja p(3) =45, niin funktion p pienin arvo on -80 | 1 p. |
| ja se saavutetaan kohdassa x =-2. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Viimeisen kohdan voi myös ratkaista laskinohjelmiston komennolla. | max 4 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Alkupiste koko tehtävästä 8: Ohjelmistolla vähintään välillä [-4,4] oikein piirretty funktion p tai derivaatan p' kuvaaja. |
9. Luottamusväli 12 p.
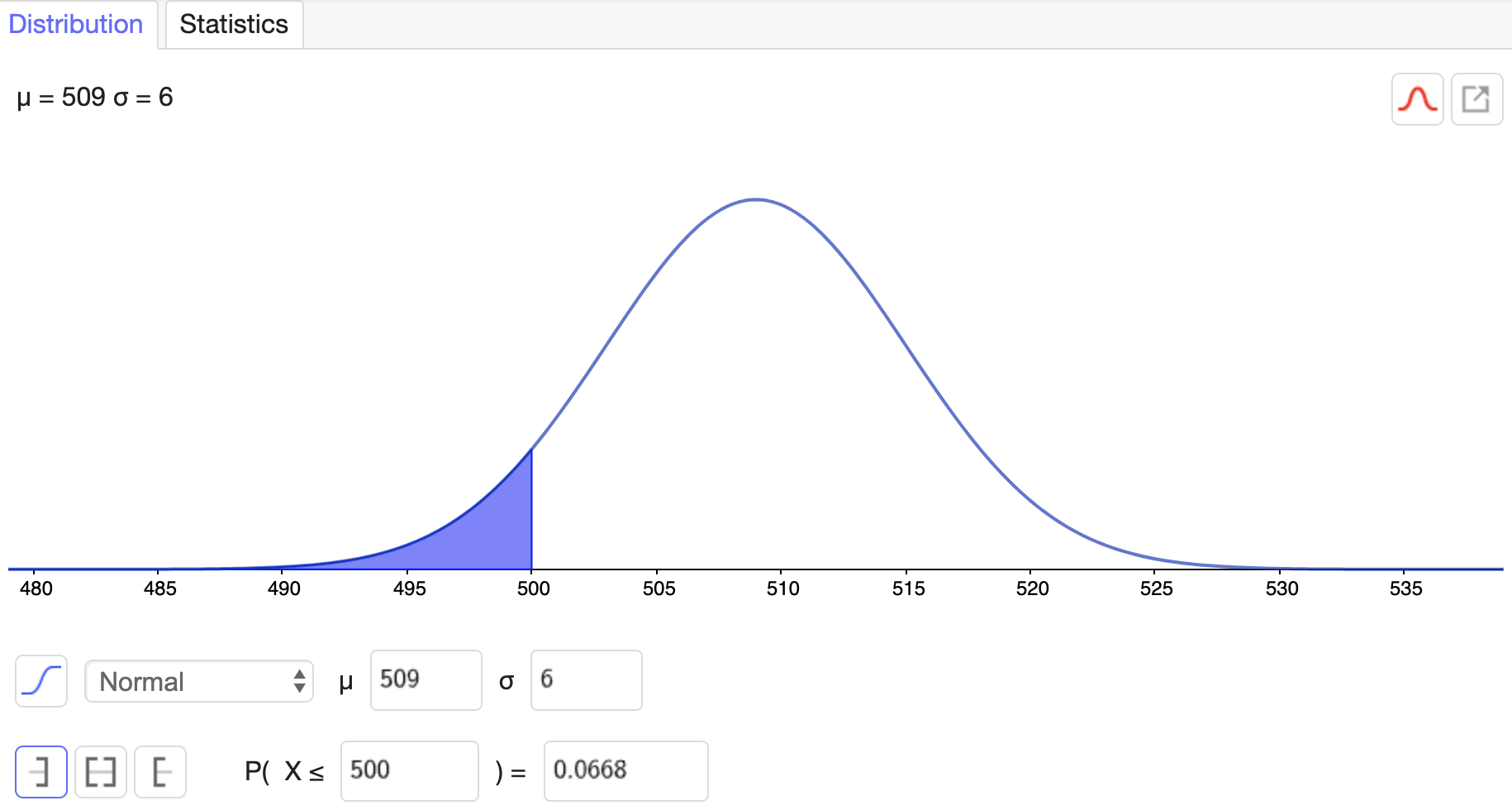
Pakkauskone on säädetty täyttämään puolen kilon muropaketteja. Laadunvalvonnassa punnitaan 100 pakettia, joiden painon keskiarvoksi saadaan 509 grammaa ja keskihajonnaksi 6,0 grammaa. Oletetaan, että paketin paino noudattaa normaalijakaumaa N(509; 6,0).
Millä todennäköisyydellä paketin paino on korkeintaan 500 grammaa? (4 p.)
Määritä paketin painon keskiarvon keskivirhe ja 95 %:n luottamusväli, eli luottamusväli 95 %:n luottamustasolla. (8 p.)
| Valittu oikea työkalu (ohjelmisto) ja | 1 p. |
| sijoitettu oikein oikeat keskiarvo (509) ja keskihajonta (6). | 1 p. |
| Alue rajattu oikein ((P(X <= 500)) | 1 p. |
| Johtopäätöksenä: Poimittu vastaus 0,0668 ~~0,067 (~~6,7 %) (vastauksen poiminnasta ei saa pistettä, jos kaikkea ei ole tehty oikein). | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Muunnosvirhe (esimerkiksi 0,0668 = 66,8 %). | –1 p. |
| NSpiren komento on \operatorname{normCDF}(-\infty,500,509,6) | |
| TAI | |
| Käytetty normaalijakaumaa | 1 p. |
| Sijoitettu kaavaan keskiarvo (509) ja keskihajonta (6). | 1 p. |
| Alue oikein ((P(X <= 500)) | 1 p. |
| Johtopäätöksenä: Vastaus (0,0668 ~~0,067 (~~6,7 %)) | 1 p. |
| Keskivirhe 0\mathrm{,}6 ja perustelu sille (esim. \frac{6}{\sqrt{100}}=0\mathrm{,}6). | 2 p. |
| Arvo 1\mathrm{,}96 (Maininta kriittisestä arvosta TAI (MAOL-)kaava, jossa 1\mathrm{,}96 näkyy) | (2 p.) |
| Luottamusvälin kaava on [\bar x - 1{,}96 \frac{s}{\sqrt{n}}, \bar x + 1{,}96 \frac{s}{\sqrt{n}}] | |
| Yksi arvo sijoitettu oikein. | 1 p. |
| Kaksi arvoa sijoitettu oikein / kolme arvoa sijoitettu oikein. | 1+1 p. |
| Vastaus oikein, kaikki tarkkuudet ja ymmärrettävät välin merkinnät käyvät. (Esimerkiksi [509-1\mathrm{,}96\cdot 0\mathrm{,}6;509+1\mathrm{,}96\cdot 0\mathrm{,}6]\approx[507\mathrm{,}8;510\mathrm{,}2] TAI 509 \pm 1\mathrm{,}17598 TAI 507\mathrm{,}8-510\mathrm{,}2 mutta välin pituus (\approx 2\mathrm{,}35) vastauksena ei kelpaa.) | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Keskivirhe on jätetty sieventämättä (6 /sqrt(100)). | –1 p. |
| Laskettu vain toinen raja. | max 6 p. |
| Virhe keskivirheen laskemisessa, muutoin loppu on laskettu oikein (0+2+1+2+1). | max 6 p. |
| Luottamusvälin kaavassa näkyy keskivirheen lauseke, keskivirhettä ei kuitenkaan ole ilmoitettu (0+2+1+2+1). | max 6 p. |
| Käytetty t-jakauman luottamusvälin kriittistä arvoa 1,98 (luottamusväli 509 +-1,19053). | max 8 p. |
| Keskivirheen kaavasta (MAOL) ei vielä pisteitä. | |
| Ohjelmistossa kriittistä arvoa vastaa oikean menetelmän oikein valittu luottamustaso (rivin pisteet 1+1) (NSpiressä oletuksena oikea 0,95) | |
| Pelkkä kuvakaappaus (0+2+1+2+0). | max 5 p. |
B2-osa
10. Matematiikan merkintöjä 12 p.
Kuinka seuraavat sanalliset kuvaukset voidaan ilmaista symbolein?
Valitse parhaiten soveltuva vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 1 p. tai 2 p., väärä vastaus 0 p., ei vastausta 0 p.
Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.
10.1 Luvun 6 kuutiojuuri. 1 p.
- root3(6) (1 p.)
10.2 Parilliset kokonaisluvut. 1 p.
- 2 k, k in ZZ (1 p.)
10.3 Luvun 7/5 käänteisluvun ja vastaluvun summan itseisarvo. 2 p.
- |5/7 +(-7/5)| (2 p.)
10.4 Luvut A ja B ovat suoraan verrannolliset verrannollisuuskertoimella k. 1 p.
- A /B =k (1 p.)
10.5 Kun kerrotaan kaksi samakantaista potenssia, niin eksponentit lasketaan yhteen. 1 p.
- x^n x^m =x^(n +m) (1 p.)
10.6 Tuotteen lopullinen hinta, kun alkuperäistä hintaa 129 € alennetaan ensin 10 % ja alennettua hintaa myöhemmin vielä 20 %. 1 p.
- 0,8 *0,9 *129 € (1 p.)
10.7 Lukusuoran pisteen x etäisyys pisteestä -2 on 3. 1 p.
- |x -(-2)| =3 (1 p.)
10.8 Tason pisteen (x, y) etäisyys pisteestä (1, -3) on 4. 2 p.
- sqrt((x -1)^2 +(y +3)^2)) =4 (2 p.)
10.9 Suorien 2 x -3 y =1 ja -x +4 y =-2 leikkauspiste. 1 p.
- {2 x -3 y =1, -x +4 y =-2} (1 p.)
10.10 Funktion f arvo kohdassa 2 on suurempi kuin funktion g arvo kohdassa -3. 1 p.
- f(2) > g(-3) (1 p.)
11. Rokottamisen tehokkuus 12 p.
Tutkijat ovat kehittäneet yksinkertaistetun mallin rokottamisesta viruspandemiassa. Mallin mukaan viruspandemia saadaan maassa hallintaan, jos H >= (1 -1/R_0) /E. Tässä
R_0 > 0 on viruksen perusuusiutumisluku
E > 0 on rokotteen tehokkuus
H on rokotettujen osuus maan väestöstä.
Muuttujat E ja H ovat prosenttilukuja sadasosina, eli esimerkiksi 1 % on 0,01.
Oletetaan, että R_0 =3. Määritä pienin mahdollinen H, jolla viruspandemia saadaan hallintaan rokotteella, jonka tehokkuus E on 80 %. (4 p.)
Mutaation seurauksena perusuusiutumisluku kasvaa arvoon 4,5. Mikä on rokotteen pienin mahdollinen tehokkuus E, jolla viruspandemia saadaan hallintaan, jos H on 80 %? (4 p.)
Anna esimerkki näiden kolmen muuttujan arvoista, joilla viruspandemiaa ei voi mallin mukaan saada hallintaan. (4 p.)
| Ryhdytty käyttämään (epä)yhtälöä H >= (1 -1/R_0) /E. | 1 p. |
| Sijoitettu R_0 =3 ja E =0,80 oikein kaavaan (1 -1/R_0) /E. | 1 p. |
| Saatu H:lle alaraja (1 -1/3) /0,80 =0,8333… | 1 p. |
| Pyöristetty yhden tai kahden merkitsevän numeron tarkkuuteen: 0,83 TAI 0,84 TAI 0,8 TAI 0,9. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Sijoitettu E =0,80 kaavaan H >= (1 -1/R_0) /E. | max 2 p. |
| Vastausrivin pisteen voi saada järkevällä väärällä vastauksella, jos esimerkiksi sijoittanut vahingossa R_0 =4,5 ja laskut on oikein. |
| Muokattu (epä)yhtälö muotoon E >= (1 -1/R_0) /H tai E = (1 -1/R_0) /H. | 1 p. |
| riippumaton Sijoitetaan R_0 =4,5 ja H =0,80 oikein kaavaan (1 -1/R_0) /H. | 1 p. |
| Saatu E:lle alaraja (1 -1/4,5) /0,80 =0,97222… | 1 p. |
| Pyöristetty kahden merkitsevän numeron tarkkuuteen: 0,97 ( =97 % ) TAI 0,98 | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Ohjelmistoa käytettäessä (epä)yhtälöä ei tarvitse muokatta muotoon E >= (1 -1/R_0) /H. | |
| Pyöristetty vastaus ylöspäin tarkkuuteen 1,0 tai 1. | –1 p. |
| Sijoitettu H =80 kaavaan (1 -1/R_0) /H. | max 2 p. |
| Vastausrivin pisteen voi saada järkevällä väärällä vastauksella, esimerkiksi sijoitettu vahingossa R_0 =3 ja laskut oikein. |
| Annettu sallitut arvot ainakin kahdelle muuttujalle (R_0 > 0, 0 < E <= 1 ja 0 <= H <= 1). | 1+1 p. |
| Laskettu kolmannen muuttujan arvon alaraja kahden annetun muuttujan perusteella ja todettu, että laskemalla saatu kolmannen muuttujan arvon alaraja on mahdoton TAI osoitettu, että kolmella sallitulla muuttujan arvolla epäyhtälö H >= (1 -1/R_0) /E ei toteudu (pisteitä ei voi jakaa). | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Esimerkki neljän pisteen vastauksesta: | |
| Jos rokote on liian tehoton verrattuna viruksen uusiutumislukuun, ei pandemiaa saada tukahtumaan. Jos esimerkiksi R =16 ja rokotteen teho 80 %, saataisiin rokotettavan väestön osuudeksi (1 -1/16) /0,80 ~~1,17. Väestöstä pitäisi rokottaa yli 100 prosenttia, mikä on mahdotonta. |
12. Maailman väestö 12 p.
Taulukossa on esitetty maailman väestömäärä vuodesta 1950 vuoteen 2020.
Mallinna väestömäärää sovittamalla aineistoon regressiosuora y =a +bx kun x on vuosi ja y väestömäärä. (4 p.)
Väestönkasvua voi mallintaa myös lukujonolla y_n =c q^n, missä n on vuosi ja y_n on väestömäärä. Määritä parametrit c ja q käyttämällä vuosien 2010 ja 2020 väestömääriä. Vaihtoehtoisesti voit käyttää mallia y_n =c e^kn, joka on käytössä tietyissä ohjelmistoissa. (4 p.)
Määritä ennusteet vuoden 2040 väestömäärästä osatehtävien 12.1 ja 12.2 mallien perusteella. (2 p.)
Arvioi osatehtävien 12.1 ja 12.2 mallien hyviä tai huonoja puolia. Mainitse kummastakin mallista yksi seikka. (2 p.)
| Oikea vastaus y=0\mathrm{,}0769x-147\mathrm{,}7117 TAI y=76{,}9x-147711{,}7. | 2 p. |
| riippumaton Perustelu: Pisteet piirretty sopivasti ohjelmistolla, | (1 p.) |
| ja käytetty käsky on näkyvissä. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kaikki tarkkuudet kelpaavat. | |
| Sovitettu muuta kuin suoraa. | +0 p. |
| Yhtälöt cq^2010 =6957 ja cq^2020 =7795. | 1+1 p. |
| Yhtälöparin ratkaiseminen aloitettu järkevästi tai annettu sopiva käsky. | 1 p. |
| Oma yhtälöpari ratkaistu oikein (q ~~1,0114 ja c ~~8,207 *10^(-7)). | 1 p. |
| TAI | |
| q^{10}=\frac{7\,795}{6\,957}, joten q\approx 1\mathrm{,}0114. | 1+1 p. |
| cq^{2010}=6\,957, joten c=\frac{6\,957}{q^{2010}}\approx 8{,}207\cdot 10^{-7} | 1+1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Jos on sovitettu kahteen pisteeseen eksponentiaalista käyrää, niin pisteytys samalla periaatteella kuin osatehtävässä 12.1. HUOM! Jos tarkkuus on väärin, voi ohjelma näyttää, että c=0, tästä | –1 p. |
| Sovitettu eksponentiaalista käyrää kaikkiin pisteisiin. | 1 p. |
| Osa laskinohjelmista ei anna negatiivista ratkaisua q. Tämän vuoksi hyväksytään myös virheellinen vastaus q\approx -1\mathrm{,}0114. |
| Sijoitettu 2040 oikeantyyppiseen, mutta mahdollisesti virheelliseen yhtälöön (lineaarinen tai eksponentiaalinen). | 1 p. |
| Kummankin mallin mukainen vastaus yksiköineen. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Oikea lineaarinen malli: 9,2 miljardia; oikea eksponentiaalinen malli 9,1 miljardia neljällä desimaalilla laskettuna ja 9,8 miljardia viidellä desimaalilla laskettuna. | |
| Eksponentiaalisen mallin antaman arvion suuruus riippuu huomattavasti käytetyistä likiarvoista. |
| Yksi hyvä selitys tai kaksi kohtuullista selitystä. | (1 p.) |
| Kaksi hyvää selitystä, yksi kummastakin mallista. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Selitysten pitää koskea malleja. | |
| Mukana ylimääräisiä virheellisiä selityksiä. | –1 p. |
| Yksi malleja keskenään vertaileva arviointi voi tuottaa kaksi pistettä. | |
| Esimerkkejä hyvistä selityksistä: | |
| Lineaarisen mallin väestömäärä on ollut negatiivinen. | |
| Väestö ei voi kasvaa ikuisesti mallin mukaan, koska maapallon kantokyky ylittyy. | |
| Osatehtävän 12.2 eksponentiaalinen malli on kehitetty vain kahden pisteen pohjalta, lineaarinen malli huomioi paremmin kokonaisuutta. | |
| Esimerkkejä kohtuullisesta selityksistä: | |
| Mallissa väestö aina kasvaa, vaikka joskus on sotia ja nälänhätää. | |
| Lineaarinen malli ei kulje kaikkien pisteiden kautta. | |
| Esimerkkejä nollan pisteen selityksistä: | |
| Ensimmäisessä mallissa ei oteta huomioon väestömäärissä tapahtuvia muutoksia. |
| Tehtäväkohtaiset erillisohjeet | |
| Alkupiste: Pisteet on piirretty sellaisessa mittakaavassa, josta näkyy, etteivät ne ole samalla suoralla. | |
| Muuttujia (yksikköjä) ei tarvitse selittää osatehtävissä 12.1 ja 12.2, jos ne ovat miljoonissa ihmisissä ja vuodet jKr. Muissa tapauksissa selitysten puutteesta | –1 p. |
13. Peräkkäiset kruunat 12 p.
Kolikkoa heitetään useita kertoja peräkkäin. Tällöin merkintä F_n ilmaisee kaikkien sellaisten tapausten lukumäärän, joissa n:ssä heitossa esiintyy vähintään kaksi peräkkäistä kruunaa. Tiedetään, että palautuskaava
F_(n +3) =2 F_(n +2) -F_n +2^n
pätee, kun n >= 1.
Määritä F_1, F_2 ja F_3 laskemalla eri tapausten lukumäärät. (4 p.)
Kolikkoa heitetään kuusi kertaa. Millä todennäköisyydellä saadaan vähintään kaksi peräkkäistä kruunaa? (4 p.)
Kolikkoa heitetään kuusi kertaa. Millä todennäköisyydellä saadaan vähintään kaksi kruunaa? (4 p.)
| riippumaton Jos kolikkoa heitetään kerran, ei voida saada kahta peräkkäistä kruunaa, eli F_1 =0. | 1 p. |
| riippumaton Jos kolikkoa heitetään kahdesti, on yksi mahdollisuus saada kaksi peräkkäistä kruunaa, eli F_2 =1. | 1 p. |
| riippumaton Ainoastaan ne jonot kelpaavat, joissa on vain kahtena ensimmäisenä kruuna tai vain kahtena viimeisenä kruuna tai kaikkina kruuna. Vaihtoehtoja on siis 3. Siispä F_3 =3. | 2 p. |
| F_4 =2 F_3 -F_1 +2^1 =2 *3 -0 +2 =8. | 1 p. |
| F_5 =2 F_4 -F_2 +2^2 =2 *8 -1 +4 =19. | 1 p. |
| F_6 =2 F_5 -F_3 +2^3 =2 *19 -3 +8 =38 -3 +8 =43. | 1 p. |
| Kaksi peräkkäistä kruunaa saadaan siis todennäköisyydellä 43/64 (~~0,67). | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Laskettu omilla järkevillä kohdan 13.1 arvoilla F_1, F_2 ja F_3 | max 4 p. |
| TAI | |
| Järkevä yritys (taustalla jokin systeemi) esimerkiksi taulukoimalla eri vaihtoehtoja. | 1 p. |
| Kaikki tapaukset löydetty (simulaatiolla ei pisteitä). | 1 p. |
| Perustelu, ettei muita tapauksia ole (esimerkiksi koko ohjelmakoodi toimiva ja näkyvissä). | 1 p. |
| Todennäköisyyden laskeminen (omien suotuisten tapausten lukumäärä jaettuna kaikkien tapausten oikealla lukumäärällä). | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Vastatapahtuma sille, että saadaan vähintään kaksi kruunaa, on se, että saadaan korkeintaan yksi kruuna, eli ei yhtään kruunaa tai täsmälleen yksi kruuna. | 1 p. |
| Todennäköisyys sille, ettei saada yhtään kruunaa, on 1 /2^6. | 1 p. |
| Todennäköisyys sille, että saadaan tasan yksi kruuna, on ((6), (1)) 1/2^6. | 1 p. |
| Kysytty todennäköisyys on siis 1 -1 /2^6 -((6), (1)) 1/2^6 =57/64 (~~0,89). | 1 p. |
| Vastatapahtumassa tasan yhden kruunan todennäköisyydestä puuttuu binomikerroin (1+1+0+0). | max 2 p. |
| TAI | |
| Laskettu ainakin yksi lukumäärä oikein tapauksista 2 kruunaa, 3 kruunaa ja niin edelleen. | 1 p. |
| Kaikki oikein (((6), (2)) =15, ((6), (3)) =20, ((6), (4)) =15, ((6), (5)) =6, ((6), (6)) =1) | 1 p. |
| Laskettu näiden summa (15 +20 +15 +6 +1 =57). | 1 p. |
| Jaettu luvulla 2^6 (57/64 (~~0,89)). | 1 p. |
| TAI | |
| Laskettu ainakin yksi todennäköisyys oikein tapauksista 2 kruunaa, 3 kruunaa, jne. 15/64 (~~0,23437), 20/64 (~~0,3125), 15/64 (~~0,234375), 6/64 (~~0,09375), 1/64 (~~0,015625) | 1 p. |
| Kaksi tapausta oikein. | 1 p. |
| Kaikki tapaukset oikein. | 1 p. |
| Laskettu näiden summa (57/64 (~~0,89)). | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Luettelosta puuttuu binomikertoimet (1+0+0+1). | max 2 p. |
| TAI | |
| Otettu käyttöön ohjelmisto binomijakauman tutkimiseen. | 1 p. |
| Sijoitettu parametrit p ja n oikein. | 1 p. |
| Valittu oikeat arvot satunnaismuuttujalle. | 1 p. |
| Annettu vastaus. | 1 p. |
| Ohjelmointiratkaisu (esimerkiksi Python) pisteytetään kuten osatehtävässä 13.2. |
| Tehtäväkohtaiset erillisohjeet | |
| Osatehtävissä 13.2 ja 13.3 kelpaa murtolukuvastaus tai likiarvo (kaikki tarkkuudet paitsi vastaus 1 käyvät) |