Beskrivningar av goda svar: SV – Matematik, kort lärokurs
19.9.2023
Slutgiltiga beskrivningar av goda svar 9.11.2023
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal i den högra kolumnen för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i parentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Terminologi
- ''Svar räcker'' betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- ''Startpoäng'' betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- ''maxN'' betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- ''Svaret endast som närmevärde'' betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (t.ex. noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (t.ex. e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (t.ex. e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (t.ex. x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (t.ex. parenteser som fattas men korrekt beräknat; =-tecknet använt ''i kedja'', m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Instruktioner för anvisningar med tre kolumner:
- Examinanden får poäng från idékolumnen om hen har börjat utföra den nämnda operationen, även om genomförandet skulle vara bristfälligt.
- En beräkning eller en formel i genomförandekolumnen visar hur idén ser ut då den är korrekt utförd.
- Stoppvillkor: från varje rad ska man få minst hälften av radens poäng, nedåt avrundade, för att man ska kunna fortsätta.
- Om stoppvillkoret inte uppfylls, dvs. om det ännu finns poäng som kan delas ut på följande rader, så kan examinanden ännu få alla poäng från de följande raderna, där det inte explicit finns något hinder för att hen inte ska kunna få poängen.
Del A
1. Funktioner och talföljder 12 p.
Välj korrekt alternativ. Svaren behöver inte motiveras. Rätt svar 2 p., fel svar 0 p., inget svar 0 p.
1.1 2 p.
- 6 (2 p.)
1.2 2 p.
- 4 (2 p.)
- +-4 (1 p.)
1.3 2 p.
- x^3 +x^2 (2 p.)
- x^3 +x^2 +4 (1 p.)
1.4 2 p.
- 6 x^2 +12 (2 p.)
1.5 2 p.
- 13 (2 p.)
1.6 2 p.
- 11 (1 p.)
- 15 (2 p.)
1.3 Ett svar som är felaktig men i rätt riktning: x^3+x^2+4. (1 p.)
1.6 Ett svar som är felaktig men i rätt riktning: 11. (1 p.)
2. I klädbutiken 12 p.
Det ursprungliga priset på ett par jeans är 56,00 euro och på en rea sänks priset med 30 %. Vilket är det sänkta priset? (4 p.)
Det ursprungliga priset på en jacka är 79,00 euro och det sänkta priset är 55,30 euro. Hur stor är rabatten i procent? (4 p.)
Mervärdesskatteprocenten på kläder är 24 %. Hur många euro av en skjortas försäljningspris på 45,00 euro utgörs av mervärdesskatt? (4 p.)
| Koefficienten 0,7 ELLER 0{,}3 \cdot 56 = 16{,}80 | 2 p. |
| Det nedsatta priset är 0{,}7\cdot 56{,}00=39\mathrm{,}20 (euro) ELLER 56{,}00-16{,}80 = 39{,}20 (euro). Denna noggrannhet krävs. | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Svar 39,2. | –0 p. |
| Det nya priset är \frac{55\mathrm{,}30}{79}=0\mathrm{,}7=70 procent av det ursprungliga priset ELLER 79{,}00-55{,}30 =23{,}70 (euro). | 2 p. |
| Rabatten är alltså 30 procent ELLER \frac{23{,}70}{79}=0{,}30 = 30 %. | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Svar och kontollberäkning. | 2 p. |
| Endast svar. | 0 p. |
| Momsen utgör 24 procent av det skattefria priset. Det här kan framgå av att koefficienten 1{,}24 används på ett någorlunda korrekt sätt. | (1 p.) |
| Ekvationen 1{,}24x = 45 för det skattefria priset x. | 1 p. |
| Detta ger x=\frac{45}{1{,}24}\approx 36{,}29 (euro). | 1 p. |
| Storleken på momsen är alltså 45{,}00-36{,}29\approx 8\mathrm{,}71 (euro). | 1 p. |
| ELLER | |
| \frac{45}{1\mathrm{,}24}\cdot 0\mathrm{,}24\approx 8\mathrm{,}71 (euro). | 4 p. |
| Specifika anvisningar för deluppgiften | 1 p. |
| Examinanden har endast beräknat 0{,}24\cdot 45 eller 0{,}76\cdot 45. | 0 p. |
| I den här uppgiften krävs en noggrannhet på en cent. |
| Specifika anvisningar för uppgiften | |
| I enskilda deluppgifter krävs inte förklaringar. Om det inte finns någon förklaring eller ens ett ord i hela uppgiften, för brister i förklaringar: | max 11 p. |
| Allmänt avdrag för svaga beteckningar: Om det i uppgiften förekommer ekvationer i formen 56-30 \ \%=39{,}20 eller motsvarande, så | –1 p. |
3. Obekanta variabler 12 p.
I figur finns linjen y =a x +b, vars koefficienter a och b är heltal. Avgör utgående från figuren koefficienternas värden och motivera hur du kom fram till lösningen. (4 p.)
Lös ut p som ett bråktal ur ekvationen (3/5 +3/4) *p =3/5. (2 p.)
Lös ut q som ett bråktal ur ekvationen (1/3 -1/2) /q =1/2. (2 p.)
Lös ut x ur ekvationen (4 n^2^3 *(n^2)^3) /2 n *x =8 n^10. (4 p.)
| Korrekt idé för hur man beräknar riktningskoefficienten: Linjen går genom punkterna (0,-2) och (1,1), riktningskoefficienten är alltså k=\frac{1-(-2)}{1-0} ELLER motsvarande muntlig förklaring. | |
| \bullet\, a=k=3. | |
| Korrekt idé om koefficienten b (y-koordinaten för skärningspunkten mellan linjen och y-axeln (0,-2)). | 1 p. |
| \bullet\, b=-2. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Koefficienterna räcker som svar, linjens ekvation behövs inte. | |
| Examinanden har gissat linjens ekvation och testat gissningen i två punkter. | 3 p. |
| Ekvationen \left(\frac{3}{5}+\frac{3}{4}\right)\cdot p=\frac{3}{5} förenklas till formen \left(\frac{1}{5}+\frac{1}{4}\right)\cdot p=\frac{1}{5} ELLER \frac{27}{20}\cdot p = \frac{3}{5} ELLER \frac{27}{20}\cdot p = \frac{12}{20}. | 1 p. |
| Alltså är \frac{4+5}{20}p=\frac{1}{5}, dvs. p=\frac{4}{9} (svaret ska ges som ett bråktal). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Ett litet räknefel som inte förenklar uppgiften på ett väsentligt sätt. | –1 p. |
| Svar och kontrollberäkning. | 1 p. |
| Ekvationen \left(\frac{1}{3}-\frac{1}{2}\right): q=\frac{1}{2} förenklas till formen -\frac{1}{6}:q=\frac{1}{2}. | 1 p. |
| Alltså är q=-\frac{1}{6}\cdot 2=-\frac{1}{3} (svaret ska ges som ett bråktal). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Om det ingår endast ett fel i svaret och uppgiften inte förenklas på ett väsentligt sätt, så | 1 p. |
| Svar och kontrollberäkning. | 1 p. |
| 4n^{2^3}\cdot (n^2)^3 = 4n^8\cdot n^6. | 1 p. |
| Uttrycket \frac{4n^{2^3}\cdot (n^2)^3}{2n}\cdot x har förenklats till formen 2n^{13}x ELLER n i nämnaren har eliminerats på ett korrekt sätt. | 1 p. |
| Examinanden har löst ut variabeln x ur det ursprungliga eller det modifierade (möjligen felaktiga) uttrycket, exempelvis x=\frac{8n^{10}}{2n^{13}}. | 1 p. |
| Alltså är x=4n^{10-13}=4n^{-3} eller \frac 4{n^3}. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Ett potensfel för variabeln n, såsom n^{2^3}=n^6 eller ett annat mindre fel. | max 3 p. |
| Felet x=8n^{10}-2n^{13} i lösningen av variabeln x. | max 2 p. |
| Specifika anvisningar för uppgiften | |
| Om man i deluppgifterna 3.2 och 3.3 har använt närmevärden, eller om decimalvärden har ändrats till bråktal utan motiveringar eller om svaret har lämnats oförenklat, avdrag för hela uppgiften | –1 p. |
4. Pythagoreiska taltripplar 12 p.
De positiva heltalen a, b och c bildar en pythagoreisk taltrippel, om a^2 +b^2 =c^2.
De här taltripplarna kan bildas på följande sätt. Anta att m och n är positiva heltal för vilka m > n. Då bildar talen a =m^2 -n^2, b =2 mn och c =m^2 +n^2 en pythagoreisk taltrippel.
Bilda någon pythagoreisk taltrippel med ovanstående metod. (3 p.)
Ge ett exempel på tre positiva heltal som inte bildar en pythagoreisk taltrippel. (3 p.)
Bestäm talen m och n då en pythagoreisk taltrippel bildas av talen a =15, b =8 och c =17. (3 p.)
Motivera följande: om a, b och c är bildade med hjälp av talen m och n som i den inledande texten, så är a^2 +b^2 =c^2. (3 p.)
| Examinanden har satt in konkreta positiva heltalsvärden på m och n, för vilka m>n, i uttryckena m^2-n^2, 2mn och m^2+n^2. | 1 p. |
| Uttryckens värden är beräknade. | 1 p. |
| Examinanden har på ett klart sätt presenterat de uträkningar där talvärdena på variablerna a, b, c, m och n explicit syns (m=\text{tal}, n=\text{tal}, osv.). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| En Pythagoreisk taltrippel har angetts utan att den givna metoden använts. | +0 p. |
| Examinanden har i övriga deluppgifter angett m=4 och n=1, av vilket hen fått a=15, b=8, c=17, utan koppling till deluppgift 4.1. Poäng för den här deluppgiften | +0 p. |
| Examinanden har angett positiva heltal (a, b och c), som inte bildar en Pythagoreisk taltrippel. | 1 p. |
| poäng oberoende av de ovanstående raderna Utförda insättningar a^2+b^2 och c^2. | 1 p. |
| Examinanden har beräknat värdena och konstaterat att a^2+b^2 \neq c^2. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| På tredje raden räcker det med att konstatera olikheten utan uträkningar, om talen är valda så att a, b \ge c eller olikheten på motsvarande sätt är uppenbar. | |
| Talen räcker, man behöver inte använda beteckningarna a, b och c. |
| Då m=4 och n=1, får vi a=m^2-n^2=4^2-1^2=15, b=2mn=2 \cdot 4 \cdot 1=8 och c=4^2+1^2=17. | 1 p. |
| Ett försök att bevisa att det inte finns andra lösningar. | 1 p. |
| Bevisat att det inte finns andra lösningar (man har exempelvis angett en tabell med talen m, n, a, b, c, då 4 \geqslant m > n \geqslant 1, och konstaterat att m \leqslant 4, eftersom 8=b=2 \cdot m \cdot n). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Endast svar m=4 och n=1. | 0 p. |
| ELLER | |
| Examinanden har eliminerat m eller n ur ekvationsparet (exempelvis a+c=(m^2-n^2)+(m^2+n^2) = 2m^2 eller 17-15=(m^2+n^2)-(m^2-n^2) = 2n^2). | 1 p. |
| Hen har satt in de givna värdena (t.ex. 32=2 m^2 eller 2=2n^2) och löst ut värdet på den ena variabeln. | 1 p. |
| Den egna lösningen har satts in i den ena av ekvationerna och den andra variabeln har beräknats ELLER man har substituerat den egna lösningen i den tredje ekvationen (som inte tillhör ekvationsparet) och löst ut den andra variabeln och granskat att den uppfyller åtminstone den ena av de egna ursprungliga ekvationerna. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Ekvationen m^2=16 är löst utan mellansteget \pm 4. | –0 p. |
| ELLER | |
| 8=b=2 \cdot m \cdot n, dvs. m \cdot n=4=2 \cdot 2 och examinanden har sökt efter lösningar från mängden av de positiva heltalen. | 1 p. |
| (Lösningarna är "m=4 och n=1" eller "m=n=2" eller "m=1 och n=4".) | 1 p. |
| Den enda möjliga lösningen är m=4 och n=1 (eftersom m>n). | 1 p. |
| Insättning av a=4^2-1^2=15 och c=4^2+1^2=17. | 1 p. |
| Insättning av a^2+b^2=(m^2-n^2)^2+(2mn)^2 eller c^2=(m^2+n^2)^2. | 1 p. |
| Beräknat (m^2-n^2)^2+(2mn)^2 = m^4-2 m^2 n^2 + n^4 + 4 m^2 n^2. | 1 p. |
| Examinanden har avlägsnat alla parenteser, förenklat och konstaterat att uttrycken är lika stora. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Prövning med talvärden. | +0 p. |
Del B1
5. Skidresa 12 p.
Inför en skidresa reserverar en grupp på 32 gymnasiestuderande en buss, och kostnaderna för den delas jämnt mellan deltagarna. Fyra studerande måste avboka sin resa, vilket gör att varje deltagare till slut betalar 15 euro mera än det ursprungliga priset. Hur mycket kostade slutligen resan för en deltagare?
| Uppgiften har lösts med slutledning | |
| Uträkning eller förklaring ger talet 28. | (1 p.) |
| 28 \cdot 15 = 420 (euro) ELLER 15/4 =3{,}75 (euro) (Korrekta tal 1+1, utförande av uträkningen 1 p.) | 3 p. |
| \frac{420}{4} = 105 (euro) ELLER 3{,}75 \cdot 28 =105 (euro). (Flyttat talvärde (420 eller 3{,}75), divisorn 4 eller koefficienten 15, utförande av uträkningen 1+1+2). | 4 p. |
| 105 + 15 = ganska exakt \textbf{120} euro (Bara 120 duger, enheten krävs i svaret.). | 1 p. |
| Förklaringar där hela lösningens förlopp framgår. En poäng för förklaringen av varje enskild rad 2, 3 och 4 i det föregående. | 1+1+1 p. |
| Specifika anvisningar för denna lösning | |
| Svaret 120 euro och test av svaret, exempelvis 120\cdot 28 = 105 \cdot 32. (En gissning kommer ofta från en felaktig ekvation.) | 5 p. |
| ELLER | |
| Uppgiften har lösts med en ekvation, ett ekvationssystem eller med proportionalitet | |
| Variablerna i uppgiften är förklarade, exempelvis bussens kostnader y och det pris x, som vardera studerande betalar om resenärerna är 32 till antalet. | 1 p. |
| Ett linjärt ekvationssystem eller en ekvation har bildats. | 1 p. |
| Poäng gällande ekvationssystem/ekvationer nedan delas endast ut för ett linjärt fall. | |
| Talet 32 är koefficient för en variabel, exempelvis y=32x. | 2 p. |
| Talet 28 är koefficient för en variabel, exempelvis y=28z. | 2 p. |
| Talet 15 är tillsatt/avdraget till variabeln, exempelvis x+15. | 2 p. |
| I ett ekvationspar är den ena ekvationen korrekt ELLER i en ekvation är den ena sidan korrekt. | 1 p. |
| Ett ekvationspar eller en ekvation är korrekt, exempelvis y = 32x och y=28(x+15) eller 32x = 28(x+15) eller x/28 = (x+15)/32. | 1 p. |
| Examinanden har kommit fram till en ekvation av en variabel och löst ut variablerna eller variabeln. (I fallet ekvationspar måste man lösa ut båda variablerna eller förklara varför den ena inte behövs.) | 1 p. |
| Ett svar har bildats, exempelvis 105 + 15 = ganska exakt 120 euro. (Bara 120 duger, enheten krävs i svaret.) | 1 p. |
| Specifika anvisningar för denna lösning | |
| För poängen vid raderna 3 och 4 krävs att talen 32 och 28 är koefficienter för variablerna. Som undantag fungerar fall där det är uppenbart att parenteser glömts bort. Exempelvis 28\cdot 15 + x, där parentesen kring termen 15+x är bortglömd. För detta ges en poäng för rad 4 och en poäng för rad 5 (för rad 5 ges 2 poäng, om 15+x har framställts korrekt i något annat skede av lösningen). |
6. Tilläggstryck på frimärke 12 p.
Ögruppen Karolinerna var en koloni i det tyska kejsardömet. Kolonins första frimärkesserie producerades av tyska frimärken genom att man tryckte texten ''Karolinen'' på dem. Det finns två typer av tilläggstrycket, flackt och brant, vilkas katalogpriser är 1 800 och 180 euro. Det flacka tilläggstryckets lutningsvinkel är ca 48^{\circ} mätt från vågrät nivå och det branta tilläggstrycket har lutningsvinkeln 56^{\circ}.
Uppskatta lutningsvinkeln för tilläggstrycket på frimärket i figur . Är tilläggstrycket av typen flackt eller brant? (6 p.)
En så liten rektangel som möjligt ritas runt tilläggstrycket. Bedöm hur många procent rektangeln täcker av frimärkets area. De vita kanterna räknas inte med i frimärkets area. (6 p.)
Uppgiften kan antingen lösas med ett lämpligt program eller genom mätning av talvärden på datorns skärm. I båda alternativen måste mellanstegen i lösningssättet framgå.
| Bilden är placerad i ett koordinatsystem och man har ritat en linje i textens riktning ELLER förändringarna i y- och x-led är uppmätta från skärmen ELLER en linje i diameterns riktning är ritad. | 2 p. |
| Linjens riktningsvinkel ligger i intervallet (54^{\circ},58^{\circ}) ELLER förändringarnas förhållande ligger i intervallet (1\mathrm{,}3; 1\mathrm{,}7) ELLER diagonalens riktningsvinkel ligger i intervallet (47^{\circ},51^{\circ}). | 1 p. |
| Det är fråga om ett frimärke av den branta typen. | 2 p. |
| Motivering för hur vinkeln är bestämd ELLER 1\mathrm{,}48\approx \tan(56^{\circ}). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| En linje i textens riktning kan utgöras av två punkter på linjen, en sida i en triangel eller ett motsvarande objekt. | |
| Endast svar. | 0 p. |
| Som motivering räcker exempelvis en skärmdump där storleken på vinkeln som en programvara ger framgår. Kommandofönstret behöver inte vara synligt. | |
| Man kan också lösa uppgiften genom att rotera bilden så att texten är vågrät. | max 6 p. |
| Examinanden har ritat vinklar för både den flacka och den branta typen, men inte på frimärket eller på ett sätt som inte heller i övrigt är klart kopplat till frimärket: 0+1+2+1. | max 4 p. |
| Examinanden har endast ritat vinkeln för den branta typen, men inte på frimärket eller på ett sätt som inte heller i övrigt är klart kopplat till frimärket: 0+1+1+0. | ma 2 p. |
| Startpoäng: Bilden är placerad i en programvara. |
| Linjer och deras normaler är ritade kring texten och en rektangel är ritad genom dessa linjers skärningspunkter. Rektangelns area har bestämts. En rektangel är ritad genom att man använt det orangefärgade områdets hörn. Rektangelns area har bestämts.
| 4 p. |
| Areornas förhållande \frac{9\mathrm{,}18}{60\mathrm{,}96}\approx exakt \textbf{15 %}. | 2 p. |
| ELLER | |
| Frimärkets area utan vita kanter har beräknats. | 1 p. |
| oberoende Examinanden har på ögonmått ritat en så liten rektangel som möjligt kring texten. | 2 p. |
| Arean på den egna rektangeln har beräknats. | 1 p. |
| Förhållandet mellan areorna har beräknats. | 1 p. |
| Förhållandet mellan areorna är exakt 15~\%. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Uträkningen av areorna måste dokumenteras: i skärmdumpen ska finnas kommandon, uträkningar eller förklaringar. Om detta saknas, för hela deluppgiften (raderna 1 och 3) | –1 p. |
| Längder och areor kan anges i egna enheter. Som motivering för längderna räcker konstaterandet "Jag mätte längderna från skärmen." | |
| Något felaktig rektangel och svaret 15~\%. (En poäng från den oberoende raden tas bort: 1+1+1+1+1) | max 5 p. |
| Inexakt rektangel, svaret i intervallet [13,17] men inte 15: (1+1+1+1+0) | max 4 p. |
| Rektangelns sidor är horisontella och lodräta linjer (förhållandet = 47 %): (1+0+1+1+0) | max 3 p. |
| Om areaberäkningarna inte är dokumenterade på något sätt (det syns inte ens en figur av en vettig rektangel) och svaret är utanför intervallet [13,17], så delas högst en startpoäng ut. | |
| Startpoäng: någon rektangel/fyrkant är ritad i en figur tillsammans med frimärket. | 1 p. |
7. Sportstrumpor 12 p.
En tävlingslöpare har sex stycken sportstrumpor oordnade i en korg. Tre av strumporna är betecknade med ett L och tre med ett R. Löparen tar på måfå upp två strumpor efter varandra ut korgen. Bestäm sannolikheten för att
den första strumpan har beteckningen L (2 p.)
båda strumporna har beteckningen L (4 p.)
strumporna har olika beteckningar. (6 p.)
| (Det finns tre L-strumpor, dvs.) den efterfrågade sannolikheten är \frac{3}{6}\ (=\frac{1}{2}). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Endast svar \frac12 eller 0{,}5 eller 50 % | 1 p. |
| Sannolikheten för att även den andra strumpan har beteckningen L är 2/5. | 2 p. |
| De egna sannolikheterna är multiplicerade med varandra (korrekt uträkning \frac{1}{2}\cdot \frac{2}{5}). | 1 p. |
| Som svar resultatet av multiplikationen i förenklad form (= \frac{1}{5}). Svaret är i intervallet (0, 1). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Endast uträkningar och svar. | 3 p. |
| Sannolikheten för att den andra strumpan har beteckningen R, om den första hade beteckningen L, är 3/5. | 1 p. |
| Sannolikheten för kombinationen L och R ( i den här ordningsföljden) är alltså 1/2 *3/5 =3/10. | 2 p. |
| Sannolikheten för att den första är en R-strumpa och den andra en L-strumpa är densamma som att den första är en L-strumpa och den andra en R-strumpa. | 1 p. |
| oberoende Den efterfrågade sannolikheten är alltså 2 *(3/10) =3/5. | 2 p. |
| Specifika anvisningar för denna lösning | |
| En lösning med en typisk trädmodell bedöms enligt detta. | max 6 p. |
| Trädmodellen är inte alls förklarad (exempelvis betecknat vilka fall som motsvarar L-strumpor och R-strumpor), för brister i förklaringar | –1 p. |
| Sannolikheten för den andra strumpan är fel (t.ex. 3/6): (0+2+1+2) | max 5 p. |
| Endast uträkning \frac{1}{2}\cdot \frac{3}{5}=\frac{3}{10} utan förklaringar eller fortsättning: (0+2+0+0). | max 2 p. |
| ELLER | |
| I komplementhändelsen är båda strumporna av samma typ. | 2 p. |
| Sannolikheten för detta är \frac{1}{5}+\frac{1}{5}=\frac{2}{5}. | 2 p. |
| oberoende Den efterfrågade sannolikheten är alltså 1-\frac{2}{5}=\frac{3}{5}. | 2 p. |
| Specifika anvisningar för denna lösning | |
| Bara det ena fallet i komplementhändelsen (1+1+1). | max 3 p. |
| ELLER | |
| Eftersom den första strumpan kan vara vilken som helst och den andra måste vara av den andra typen, så räcker det att granska sannolikheten för den andra strumpan. | 4 p. |
| oberoende Den efterfrågade sannolikheten är \frac{3}{5}. | 2 p. |
| Specifika anvisningar för denna lösning | |
| Bara \frac{6}{6}\cdot \frac{3}{5} = \frac{3}{5} ELLER 1\cdot \frac{3}{5} = \frac{3}{5} utan förklaringar (1+2). | 3 p. |
| Specifika anvisningar för uppgiften | |
| Svaren kan anges i decimalform, i procent eller som bråktal. |
8. Polynomfunktion 12 p.
Anta att p(x) =x^4 -4 x^3 -8 x^2 +48 x.
Beräkna derivatan p’(x) och lös ut derivatans nollställen. (4 p.)
I vilka intervall är funktionen p växande? (4 p.)
Bestäm det minsta värdet av funktionen p. I vilken punkt uppnås detta värde? (4 p.)
| Beräknad derivata p'(x) och man får ett tredjegradspolynom ELLER minst två av fyra termer i polynomet p(x) är korrekt deriverade ELLER att det av lösningen framgår att man använt rätt kommando med programvara. | 1 p. |
| Derivatafunktionen p'(x)=4x^3-12x^2-16x+48 är korrekt. | 1 p. |
| Examinanden löser korrekt ut ett nollställe till den egna derivatafunktionen, som är ett polynom. | 1 p. |
| oberoende Examinanden löser korrekt ut alla nollställen till den egna derivatafunktionen, som är ett polynom av tredje graden ELLER hen får som nollställen -2, 2 och 3 (exempelvis genom att titta på figuren). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Nollställena till derivatafunktionen kan lösas med Lös/Solve-kommandot. | |
| Beräkning av nollställena till p. | +0 p. |
| Nollställena är givna i formen (-2,0), (2,0) och (3,0). | –0 p. |
| Man gör ett teckenschema med den egna derivatans nollställen. Det krävs att derivatafunktionens värden beräknas i testpunkter och att alla nollställen ingår. ELLER Man beräknar (med programvara) extremställena till p eller derivatans nollställen och förenar informationen med grafen till p eller p'. | 2 p. |
| oberoende Polynomet är växande då -2\leq x\leq 2 eller x\geq 3 (endast detta svar duger). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Intervall som inte innehåller ändpunkterna godkänns som svar. | –0 p. |
| Ett korrekt teckenschema är - | + | - | + med nollställena -2, 2 och 3. |
| En granskning av funktionens värden i de punkter som exempelvis utifrån det egna teckenschemat utgör lokala minimiställen (punkter) till p eller nollställen till derivatan. | 1 p. |
| Insättning av de egna mimimiställena i uttrycket för p och beräkning av värdena för p i dem. | 1 p. |
| Eftersom p(-2)=-80 och p(3)=45, så är p:s minsta värde -80 | 1 p. |
| och det uppnås i punkten x=-2. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Den sista deluppgiften kan också lösas med hjälp av en programvaras kommando. | max 4 p. |
| Specifika anvisningar för uppgiften | |
| Startpoäng för hela uppgift 8: Grafen till funktionen p eller till derivatafunktionen p' har ritats korrekt med programvara åtminstone i intervallet [-4,4]. |
9. Konfidensintervall 12 p.
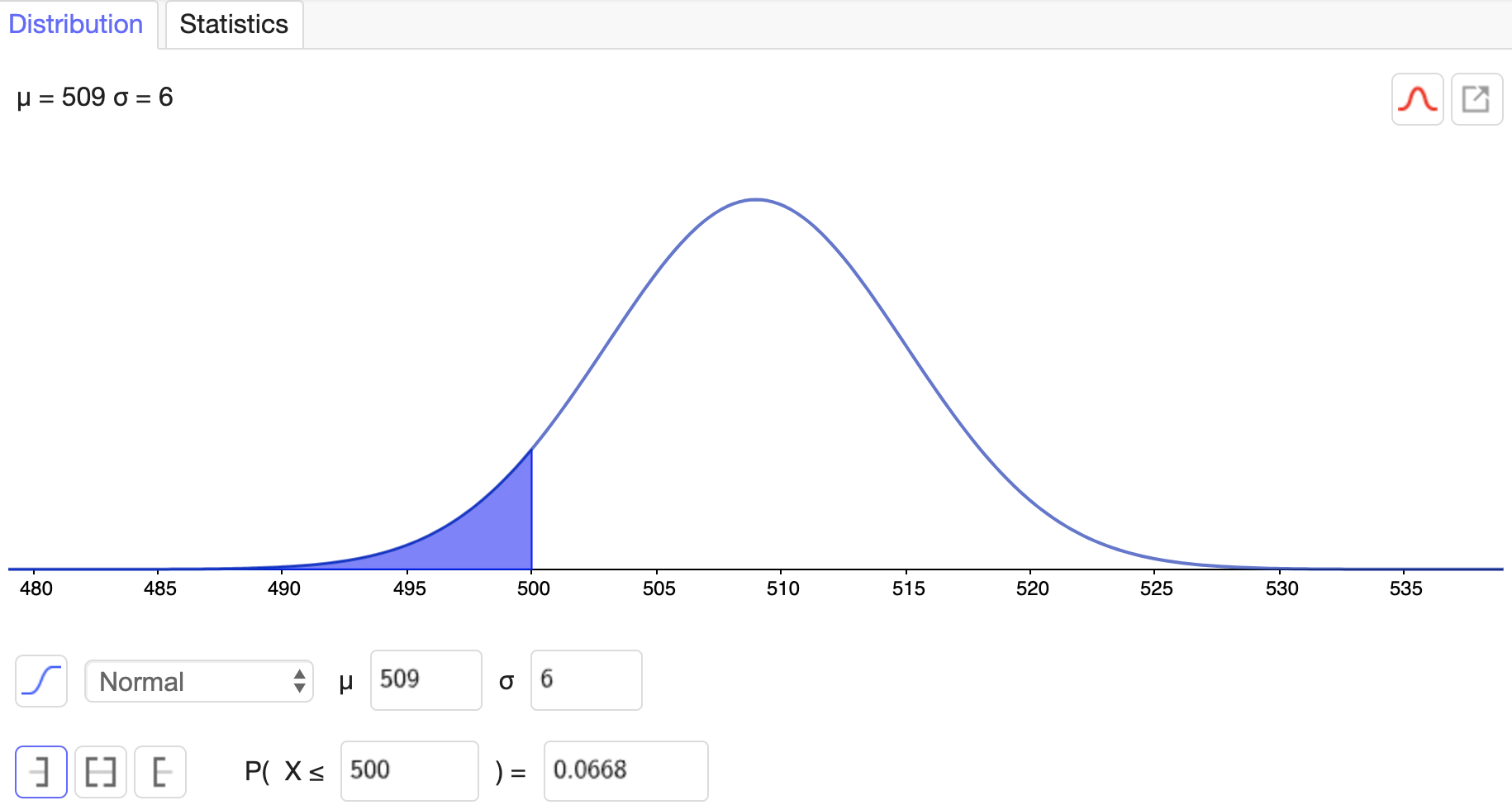
En förpackningsmaskin är inställd för att fylla flingpaket på ett halvt kilogram. I en kvalitetskontroll vägs 100 paket. Paketens vikter har medelvärdet 509 gram och standardavvikelsen 6,0 gram. Vi antar att vikten för ett paket följer normalfördelningen N(509; 6,0).
Med vilken sannolikhet är vikten för ett paket högst 500 gram? (4 p.)
Bestäm medelfelet för medelvärdet av paketens vikt och det 95-procentiga konfidensintervallet för medelvärdet, dvs. det konfidensintervall som har konfidensgraden 95 %. (8 p.)
| Examinanden har valt rätt verktyg (programvara) och | 1 p. |
| satt in korrekta värden för medelvärdet (509) och för standardavvikelsen (6). | 1 p. |
| Området är korrekt avgränsat (P(X \leq 500)) | 1 p. |
| Som slutsats: Hämtat svar 0\mathrm{,}0668 \approx 0\mathrm{,}067 \ (\approx 6,7\,\%) (man får inte poäng för hämtningen av svaret om inte allt är korrekt gjort). | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Omvandlingsfel (exempelvis 0,0668 = 66,8 %). | –1 |
| NSpires kommando är \operatorname{normCDF}(-\infty,500,509,6) | |
| ELLER | |
| Normalfördelningen har använts | 1 p. |
| Insättning av medelvärdet (509) och standardavvikelsen (6) i formeln. | 1 p. |
| Området är korrekt (P(X \leq 500)) | 1 p. |
| Som slutsats: Svar (0\mathrm{,}0668 \approx 0\mathrm{,}067 \ (\approx 6{,}7\,\%)) | 1 p. |
| Medelfelet 0\mathrm{,}6 och motivering (t.ex. \frac{6}{\sqrt{100}}=0\mathrm{,}6). | 2 p. |
| Värdet 1\mathrm{,}96 (det kritiska värdet är nämnt ELLER (MAOL-)formel där 1\mathrm{,}96 syns) | (2 p.) |
| Konfidensintervallets formel är [\bar x - 1{,}96 \frac{s}{\sqrt{n}}, \bar x + 1{,}96 \frac{s}{\sqrt{n}}] | |
| Ett värde är korrekt insatt. | 1 p. |
| Två värden är korrekt insatta / tre värden är korrekt insatta. | 1+1 p. |
| Svaret är korrekt, alla nogrannheter och begripliga intervallbeteckningar duger. (Exempelvis [509-1\mathrm{,}96\cdot 0\mathrm{,}6;509+1\mathrm{,}96\cdot 0\mathrm{,}6]\approx[507\mathrm{,}8;510\mathrm{,}2] ELLER 509 \pm 1\mathrm{,}17598 ELLER 507\mathrm{,}8-510\mathrm{,}2 men intervallets längd (\approx 2\mathrm{,}35) duger inte som svar.) | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Medelfelet oförenklat (6/\sqrt{100}). | –1 p. |
| Endast den ena gränsen är beräknad. | max 6 p. |
| Fel i beräkning av medelfelet, i övrigt är slutet korrekt beräknat (0+2+1+2+1). | max 6 p. |
| I fomeln för konfidensintervallet syns uttrycket för medelfelet, men medelfelet har inte nämnts (0+2+1+2+1). | max 6 p. |
| Man har använt det kritiska värdet 1\mathrm{,}98 för t-fördelningens konfidensintervall (konfidensintervallet 509 \pm 1\mathrm{,}19053). | max 8 p. |
| För formeln för medelfelet (MAOL) delas inte ännu ut några poäng. | |
| I programvara motsvarar det kritiska värdet rätt vald konfidensnivå med korrekt metod (radens poäng 1+1) (i NSpire är standardvärdet 0\mathrm{,}95 det rätta). | |
| Endast skärmdump (0+2+1+2+0). | max 5 p. |
Del B2
10. Beteckningar i matematiken 12 p.
Hur kan man uttrycka följande verbala beskrivningar med symboler?
Välj det mest lämpliga alternativet. Svaren behöver inte motiveras. Rätt svar 1 p. eller 2 p., fel svar 0 p., inget svar 0 p.
Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning kan du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
10.1 Kubikroten av talet 6. 1 p.
- root3(6) (1 p.)
10.2 De jämna heltalen. 1 p.
- 2 k, k in ZZ (1 p.)
10.3 Absolutbeloppet av summan av det inverterade och det motsatta talet till talet 7/5. 2 p.
- |5/7 +(-7/5)| (2 p.)
10.4 Talen A och B är direkt proportionella mot varandra med proportionalitetskonstanten k. 1 p.
- A /B =k (1 p.)
10.5 Då två potenser med samma bas multipliceras så adderar man exponenterna. 1 p.
- x^n x^m =x^(n +m) (1 p.)
10.6 Det slutliga priset på en produkt då det ursprungliga priset 129 € först sänks med 10 % och det sänkta priset senare ytterligare sänks med 20 %. 1 p.
- 0,8 *0,9 *129 € (1 p.)
10.7 Avståndet mellan punkten x och punkten -2 på tallinjen är 3. 1 p.
- |x -(-2)| =3 (1 p.)
10.8 Avståndet mellan punkten (x, y) och punkten (1, -3) i planet är 4. 2 p.
- sqrt((x -1)^2 +(y +3)^2)) =4 (2 p.)
10.9 Skärningspunkten mellan linjerna 2 x -3 y =1 och -x +4 y =-2. 1 p.
- {2 x -3 y =1, -x +4 y =-2} (1 p.)
10.10 Värdet av funktionen f i punkten 2 är större än värdet av funktionen g i punkten -3. 1 p.
- f(2) > g(-3) (1 p.)
11. Effektiviteten hos ett vaccin 12 p.
Forskare har utvecklat en förenklad modell för vaccineringen under en viruspandemi. Enligt modellen stävjas viruspandemin i ett land om H >= (1 -1/R_0) /E. Här är
R_0 > 0 virusets reproduktionstal
E > 0 vaccinets effektivitet
H andelen av ett lands befolkning som fått vaccinet.
Variablerna E och H är procenttal i hundradelar, dvs. 1 % motsvaras av 0,01.
Vi antar att R_0 =3. Bestäm det minsta möjliga H för vilket viruspandemin stävjas med ett vaccin vars effektivitet E är 80 %. (4 p.)
Som följd av en mutation stiger reproduktionstalet till värdet 4,5. Vilken är ett vaccins minsta möjliga effektivitet E för att viruspandemin ska stävjas, om H är 80 %? (4 p.)
Ge ett exempel på värden på de här tre variablerna, för vilka pandemin inte kan stävjas enligt denna modell. (4 p.)
| Examinanden har börjat använda (o)likheten H\geq \frac{1-\frac{1}{R_0}}{E}. | 1 p. |
| Korrekt insättning av R_0=3 och E=0{,}80 i formeln \frac{1-\frac{1}{R_0}}{E}. | 1 p. |
| Examinanden har fått en nedre gräns \frac{1-\frac{1}{3}}{0\mathrm{,}80}=0{,}8333\ldots för H. | 1 p. |
| Avrundat till en noggrannhet på en eller två gällande siffror: 0\mathrm{,}83 ELLER 0{,}84 ELLER 0{,}8 ELLER 0{,}9. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Insättning av E=80 i formeln \frac{1-\frac{1}{R_0}}{E}. | max 2 p. |
| Man kan få poängen för svarsraden med ett vettigt felaktigt svar, om man exempelvis i misstag satt in R_0=4{,}5 och uträkningen är korrekt. |
| Olikheten/ekvationen är omskriven i formen E\geq \frac{1-\frac{1}{R_0}}{H} eller E=\frac{1-\frac{1}{R_0}}{H}. | 1 p. |
| oberoende Korrekt insättning av R_0=4{,}5 och H=0{,}80 i formeln \frac{1-\frac{1}{R_0}}{H}. | 1 p. |
| Examinanden har fått en nedre gräns \frac{1-\frac{1}{4{,}5}}{0\mathrm{,}80}=0{,}97222\ldots för E. | 1 p. |
| Avrundat till två gällande siffrors nogrannhet: 0\mathrm{,}97 (=97\ \%) ELLER 0{,}98. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Om man använder programvara så behöver inte (o)likheten omskrivas i formen E\geq \frac{1-\frac{1}{R_0}}{H}. | |
| Svaret är avrundat uppåt till noggrannheten 1{,}0 eller 1. | –1 p. |
| Insättning av H=80 i formeln \frac{1-\frac{1}{R_0}}{H}. | max 2 p. |
| Man kan få poängen för svarsraden med ett vettigt felaktigt svar, om man exempelvis i misstag satt in R_0=3 och uträkningen är korrekt. |
| Examinanden har angett godkända värden på minst två variabler (R_0 > 0, 0 < E \leq 1 och 0 \leq H \leq 1). | 1+1 p. |
| Examinanden har beräknat värdet på den tredje variabeln utgående från två givna variabler och konstaterat att det erhållna värdet för nedre gränsen på variabeln är omöjligt ELLER så har hen visat att med tre tillåtna variabelvärden så uppfylls inte olikheten H \geq \frac{1-\frac{1}{R_0}}{E} (poäng kan inte delas). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Exempel på ett svar som är värt fyra poäng: | |
| Om vaccinet är för ineffektivt jämfört med virusets reproduktionstal så kan pandemin inte stävjas. Om exempelvis R=16 och vaccinets effekt är 80 %, så blir den andel av befolkningen som ska vaccineras \frac{1-\frac{1}{16}}{0\mathrm{,}80}\approx 1\mathrm{,}17. Över 100 procent av befolkningen borde vaccineras, vilket är omöjligt. |
12. Världens befolkning 12 p.
I tabell presenteras världens folkmängd från år 1950 till år 2020.
Skapa en modell av folkmängden genom att anpassa en regressionslinje y =a +bx till materialet, då x är året och y folkmängden. (4 p.)
Man kan också skapa en modell av befolkningstillväxten med talföljden y_n =c q^n, där n är året och y_n är folkmängden. Bestäm parametrarna c och q genom att använda folkmängderna åren 2010 och 2020. Alternativt kan du använda modellen y_n =c e^kn, som används i vissa programvaror. (4 p.)
Bestäm prognoserna för folkmängden år 2040 utgående från modellerna i deluppgifterna 12.1 och 12.2. (2 p.)
Bedöm de goda eller de dåliga sidorna med modellerna i deluppgifterna 12.1 och 12.2. Nämn en sak för vardera modell. (2 p.)
| Korrekt svar y=0\mathrm{,}0769x-147\mathrm{,}7117 ELLER y=76{,}9x-147711{,}7. | 2 p. |
| oberoende Motivering: punkterna är ritade på ett lämpligt sätt med programvara, | (1 p.) |
| och det använda kommandot är synligt. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Alla noggrannheter duger. | |
| Något annat än en linje har anpassats. | +0 p. |
| Ekvationerna cq^{2010}=6\,957 och cq^{2020}=7\,795. | 1+1 p. |
| Lösningen av ekvationsparet har påbörjats på ett förnuftigt sätt, eller så är ett passande kommando givet. | 1 p. |
| Det egna ekvationsparet är korrekt löst (q\approx 1\mathrm{,}0114 och c\approx 8{,}207\cdot 10^{-7}). | 1 p. |
| ELLER | |
| q^{10}=\frac{7\,795}{6\,957}, dvs. q\approx 1\mathrm{,}0114. | 1+1 p. |
| cq^{2010}=6\,957, dvs. c=\frac{6\,957}{q^{2010}}\approx 8{,}207\cdot 10^{-7} | 1+1 p. |
| Specifika anvisningar för deluppgiften | |
| Om man gjort en anpassning av en exponentiell kurva till två punkter fungerar poänggivningen enligt samma princip som i deluppgift 12.1. OBS! Om noggrannheten är fel så kan programmet visa att c=0, för detta | –1 p. |
| En anpassad exponentiell kurva till alla punkter. | 1 p. |
| En del av programvarorna ger inte den negativa lösningen på q. På grund av detta godkänns också det felaktiga svaret q\approx -1\mathrm{,}0114. |
| Insättning av talet 2040 i en egen ekvation i rätt riktning (linjär eller exponentiell). | 1 p. |
| Svar i enlighet med båda modellerna med enheter. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Svaret med en korrekt linjär modell är 9\mathrm{,}2 miljarder och med en korrekt exponentiell modell 9\mathrm{,}1 miljarder beräknat med fyra decimaler och 9\mathrm{,}8 miljarder beräknat med fem decimaler. | |
| De använda närmevärdena har en avsevärd betydelse för uppskattningen med den exponentiella modellen. |
| En bra förklaring eller två måttliga förklaringar. | (1 p.) |
| Två bra förklaringar, en för vardera modell. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Förklaringarna måste gälla modellerna. | |
| Överflödiga felaktiga förklaringar ingår. | –1 p. |
| En bedömning som jämför modellerna med varandra kan ge två poäng. | |
| Exempel på goda förklaringar: | |
| Folkmängden i den linjära modellen har varit negativ. | |
| Folkmängden kan inte växa för evigt enligt modellen, eftersom jordklotets bärkraft överskrids. | |
| Den exponentiella modellen i deluppgift 12.2 är utvecklad utgående från bara två punkter, den linjära modellen beaktar helheten på ett bättre sätt. | |
| Exempel på måttliga förklaringar: | |
| Folkmängden i modellen växer alltid, trots att det ibland råder krig och hungersnöd. | |
| Den linjära modellen går inte genom alla punkter. | |
| Exempel på förklaringar värda noll poäng: | |
| I den första modellen beaktas inte förändringar som sker i folkmängderna. |
| Specifika anvisningar för uppgiften | |
| Startpoäng: Punkterna är ritade i en sådan skala så att det framgår att de inte ligger på samma linje. | |
| Variablerna (enheterna) behöver inte förklaras i deluppgifterna 12.1 och 12.2, om de är givna i miljoner människor och antal år e. Kr. I övriga fall för brister i förklaringar | –1 p. |
13. På varandra följande kronor 12 p.
En slant singlas flera gånger efter varandra. Då uttrycker beteckningen F_n antalet av alla sådana fall, där det på n kast förekommer minst två på varandra följande kronor. Vi vet att rekursionsformeln
F_(n +3) =2 F_(n +2) -F_n +2^n
gäller då n >= 1.
Bestäm F_1, F_2 och F_3. genom att beräkna antalet av de olika fallen. (4 p.)
En slant singlas sex gånger. Med vilken sannolikhet får man minst två på varandra följande kronor? (4 p.)
En slant singlas sex gånger. Med vilken sannolikhet får man minst två kronor? (4 p.)
| oberoende Om slanten singlas en gång så kan man inte få två på varandra följande kronor, dvs. F_1=0. | 1 p. |
| oberoende Om slanten singlas två gånger så finns det en möjlighet att få två på varandra följande kronor, dvs. F_2=1. | 1 p. |
| oberoende Endast sådana följder duger, där bara de två första är kronor eller de två sista är kronor eller där alla är kronor. Antalet alternativ är alltså 3. Därmed är F_3=3. | 2 p. |
| F_4=2F_3-F_1+2^1=2\cdot 3-0+2=8. | 1 p. |
| F_5=2F_4-F_2+2^2=2\cdot 8-1+4=19. | 1 p. |
| F_6=2F_5-F_3+2^3=2\cdot 19-3+8=38-3+8=43. | 1 p. |
| Man får alltså två på varandra följande kronor med sannolikheten \frac{43}{64}\ (\approx 0\mathrm{,}67). | 1 p. |
| Specifika anvisningar för denna lösning | |
| Man har beräknat med egna förnuftiga värden på F_1, F_2 och F_3 hämtade från deluppgift 13.1. | max 4 p. |
| ELLER | |
| Ett förnuftigt försök (något bakomliggande system) exempelvis genom att en tabell över olika alternativ gjorts. | 1 p. |
| Alla fall har hittats (inga poäng med simulering). | 1 p. |
| En motivering för att det inte finns andra fall (exempelvis en hel programkod som är synlig). | 1 p. |
| Beräkning av sannolikheten (det egna antalet gynnsamma utfall dividerat med det korrekta antalet totala utfall). | 1 p. |
| Specifika anvisningar för denna lösning | |
| Komplementhändelsen till det att man får minst två kronor är den att man får högst en krona, dvs. ingen krona eller exakt en krona. | 1 p. |
| Sannolikheten för att man inte får någon krona är \frac{1}{2^6}. | 1 p. |
| Sannolikheten för att man får exakt en krona är \binom{6}{1}\frac{1}{2^6}. | 1 p. |
| Den efterfrågade sannolikheten är alltså 1-\frac{1}{2^6}-\binom{6}{1}\frac{1}{2^6}=\frac{57}{64} \ (\approx 0\mathrm{,}89). | 1 p. |
| I komplementhändelsen fattas binomialkoefficienten för exakt en krona (1+1+0+0). | max 2 p. |
| ELLER | |
| Åtminstone ett antal av fallen 2 kronor, 3 kronor och så vidare är korrekt. | 1 p. |
| Allt korrekt ( \binom{6}{2}=15, \binom{6}{3}=20, \binom{6}{4}=15, \binom{6}{5}=6, \binom{6}{6}=1) | 1 p. |
| Summan av dessa är beräknad (15+20+15+6+1=57). | 1 p. |
| Denna är dividerad med talet 2^6 (\frac{57}{64} \ (\approx 0\mathrm{,}89)). | 1 p. |
| ELLER | |
| Beräknat åtminstone en sannolikhet korrekt av fallen 2 kronor, 3 kronor, osv. (\frac{15}{64}\ ({\approx}0\mathrm{,}23437), \frac{20}{64}\ ({\approx}0\mathrm{,}3125), \frac{15}{64}\ ({\approx}0\mathrm{,}234375), \frac{6}{64}\ ({\approx}0\mathrm{,}09375), \frac{1}{64}\ ({\approx}0\mathrm{,}015625) ) | 1 p. |
| Två fall är korrekta. | 1 p. |
| Alla fall är korrekta. | 1 p. |
| Summan av dessa tal är beräknad (\frac{57}{64} (\approx 0\mathrm{,}89)). | 1 p. |
| Specifika anvisningar för denna lösning | |
| Binomialkoefficienterna saknas i uträkningarna (1+0+0+1). | max 2 p. |
| ELLER | |
| Examinanden har tagit i bruk programvara för att undersöka binomialfördelningen. | 1 p. |
| Parametrarna p och n är korrekt insatta. | 1 p. |
| Korrekt valda värden för slumpvariabeln. | 1 p. |
| Angivet svar. | 1 p. |
| En programmeringslösning (exempelvis Python) bedöms som i deluppgift 13.2. |
| Specifika anvisningar för uppgiften | |
| I deluppgifterna 13.2 och 13.3 duger ett svar i bråkform eller ett närmevärde (alla noggrannheter förutom svaret 1 duger). |