Hyvän vastauksen piirteet: FI – Matematiikka, lyhyt oppimäärä
20.3.2024
Lopulliset hyvän vastauksen piirteet 14.5.2024
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.
Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.
Miten pisteytysohjeita luetaan
- Ohjeen rakenne
- Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy oikeassa sarakkeessa olevaan pistemäärään.
- Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
- Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
- Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
- Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esim. derivaatan laskeminen osittain oikein).
- Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
- Suluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
- Jos erikseen ei mainita, niin vastauksen hyväksyttävä tarkkuus on yksi merkitsevä numero enemmän tai vähemmän kuin ohjeeseen kirjattu.
- Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
- Rivien riippuvuus toisistaan
- Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esim. laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
- Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
- Merkintä ylläolevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
- Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
- Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
- Teksti STOP tarkoittaa sitä, että sillä rivillä kerrotaan, minkä ehtojen pitää toteutua, jotta jatkosta saa pisteitä.
- Terminologiaa
- ''Vastaus riittää'' tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
- ''Alkupisteitä'' tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
- ''maxN'' tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
- ''Vastaus vain likiarvona'' tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.
- Vastaus oikein, muttei pyydetyssä muodossa (esim. tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esim. e^1, ln (e) tai 4^0 -2 p.
- Vastaus sieventämättä muussa tehtävässä (esim. e^1, ln (e) tai 4^0 -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esim. x =2, y04, tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.
- Matemaattisesti puutteellinen merkintä (esim. puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
A-osa
1. Perustehtäviä 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 Mikä on yhtälön 3 x -8 =34 ratkaisu? 2 p.
- x =14 (2 p.)
1.2 Mikä on yhtälön x^2 -100 =0 positiivinen ratkaisu? 2 p.
- x =10 (2 p.)
1.3 Määritä se kohta, jossa suora y=3x+12 leikkaa x-akselin. 2 p.
- x =-4 (2 p.)
1.4 Määritä se kohta, jossa suora y +2 x -6 =0 leikkaa y-akselin. 2 p.
- y =6 (2 p.)
1.5 Mikä on funktion f(x) =3 x^8 -68 arvo kohdassa x =2? 2 p.
- f(2) =700 (2 p.)
1.6 Mikä on yhtälön x^3 +2197 =0 ratkaisu? 2 p.
- x =-13 (2 p.)
2. Kulmanmetsästys 12 p.
Määritä kuviin merkityt tuntemattomat kulmat asteen tarkkuudella.
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen kohdan vastaus on kokonaisluku.
2.1 Määritä kulma \alpha. 2 p.
- 60 (2 p.)
2.2 Määritä kulma \beta. 2 p.
- 25 (2 p.)
2.3 Määritä kulma \gamma. 2 p.
- 51 (2 p.)
2.4 Määritä kulma \delta. 2 p.
- 47 (2 p.)
- –47 (1 p.)
- 43 (1 p.)
2.5 Määritä kulma \epsilon. 2 p.
- 24 (2 p.)
2.6 Määritä kulma \zeta. 2 p.
- 62 (2 p.)
3. Laina 12 p.
Paju on ottanut 135 000 euron lainan, jonka kiinteä vuosikorko on 4,5 prosenttia ja takaisinmaksuaika 12 vuotta ja jota lyhennetään kuukausittain. Laske Pajun 13. maksuerä, kun kyseessä on
annuiteettilaina. (6 p.)
tasalyhennyslaina. (6 p.)
| Määritetty kuukausikorko 0{,}375\, \% (mahdollisesti osana korkokertoimen määritystä). | 1 p. |
| Korkokerroin 1<q<2 laskettu tai ilmoitettu ja vastaa omaa korkoa. Tämä voi käydä ilmi myös implisiittisesti annuiteettikaavan käytössä. | 1 p. |
| Lyhennyserien määrä on 144. Tämä voi käydä ilmi myös implisiittisesti. | 1 p. |
| Käytetty annuiteettikaavaa A=Kq^n \frac{1-q}{1-q^n} omalla korkokertoimella (1<q<2) ja siihen liittyvällä lyhennysten määrällä (oikeat kuukausiluvut: q=1\mathrm{,}00375 ja n=144 ja vuosiluvut q=1\mathrm{,}045 ja n=12). (Pisteytys joko 0 p. tai 2 p., vain standardivähennykset.) | 2 p. |
| Lukuarvo ja vain tämä tarkkuus kelpaa täsmälleen 1215,01. | 1 p. |
| Määritetty maksuerän lyhennysosa 135\,000/144 = 937{,}50 (euroa). | 2 p. |
| Määritetty jäljellä oleva velka 135\,000-12\cdot 937\mathrm{,}50=123\, 750. (13 lyhennysosaa, 1 p.) | 2 p. |
| Määritetty maksuerän korko-osa oikein omilla lukuarvoilla (123\,750\cdot 0\mathrm{,}00375=464\mathrm{,}06). | 1 p. |
| Lukuarvo ja vain tämä tarkkuus kelpaa täsmälleen 1401,56. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Huom. Jos 1. osatehtävä puuttuu tai kuukausikorkoa ja lyhennysten määrää ei ole edes yritetty laskea siinä, voidaan lyhennyserien määrän ja kuukausikoron määrittämisen pisteet (1 + 1) antaa 2. osatehtävän vastauksen perusteella, kunhan 2. osatehtävässä luvut on annettu selkeästi, eikä vain implisiittisesti. |
4. Eksponentiaalisia kuvaajia 12 p.
Kuvassa on funktion u(x)=a\,b^x kuvaaja. Määritä vakiot a ja b. (6 p.)
Kuvassa on kuvaajat f, g ja h. Kaksi niistä ei ole muotoa v(x)=c\,d^x olevan funktion kuvaaja millään vakioilla c ja d. Perustele, mitkä kaksi. (6 p.)
| Kaksi seuraavista yhtälöistä: ab^{-1}=0{,}75, ab^0=1{,}5, ab^1=3 ja ab^2=6. | 1+1 p. |
| Päätelty joko suoraan tai kaksi yhtälöä yhdistämällä a tai b. | 2 p. |
| Päätelty toinen arvo. | 2 p. |
| TAI | |
| Huomattu, että arvo kaksinkertaistuu, kun x kasvaa yhdellä (1 p.) ja tästä päätelty, että b=2 (2 p.). | 3 p. |
| Todetaan y-akselin leikkauskohdan perusteella, että a=1{,}5. | 3 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kaikki oikeat yhtälöt hyväksytään, jos pieni epätarkkuus niin -1 p. | |
| Toinen arvo (mahdollisesti väärä) ilmestynyt tyhjästä, muodostettu yksi yhtälö ja sen perusteella ratkaistu toinen tai muuten asiallisesti päätelty toinen. | max 3 p. |
| Arvausratkaisu: Sekä a että b oikein (1 p.) + tarkistus yhdessä pisteessä (2 p.) + toisessa pisteessä (2 p.). | max 5 p. |
| Väärät arvot ja tarkistus yhdessä pisteessä. | 1 p. |
| Jos sijoitetaan arvo a=1{,}5 yhtälöön 6=ab^2, ei tarvitse perustella, miksi negatiivinen juuri ei käy. | |
| Selvennys: Ensimmäisen rivin pisteisiin tarvitaan, että on osattu lukea koordinaatistosta käyrän piste(et) ja yhdistetty tämä järkevästi käyrän yhtälöön. Yhden pisteen yhdistäminen kaavaan tuottaa yhden pisteen ja sama toiselle pisteelle tuottaa toisen pisteen. |
| Perusperiaate on perustelut (2 p.) + vastaus (1 p.). Vastauspiste edellyttää ainakin sinnepäin olevan perustelun, eli 0+1 ei ole mahdollinen. | |
| Esimerkkejä kahden pisteen perusteluista: | 2 p. |
| Kulkee origon kautta TAI on nollakohta TAI f(x) = 0 TAI leikkaa x-akselin | |
| Saa negatiivisia ja positiivisia arvoja | |
| h(x) = x + 1 | |
| Suhdevertailu (Esimerkiksi \frac{h(1)}{h(0)}=\frac{2}{1}=2 ja \frac{h(2)}{h(1)}=\frac{3}{2}\ne 2, eli ne eivät ole samat.) | |
| Esimerkkejä yhden pisteen perusteluista: | 1 p. |
| On suora TAI lineaarinen TAI affiini | |
| h(x) = ax + b | |
| Kuvaaja menee nollan alapuolelle. | |
| Esimerkkejä nollan pisteen perusteluista: | 0 p. |
| Saa negatiivisia arvoja |
| Osatehtäväkohtaiset erillisohjeet | |
| Alkupiste: Yritetty ainoastaan perustella, miksi g on eksponentiaalinen. (Huomaa, että kuvaajan avulla tätä ei voi aukottomasti perustella.) | max 2 p. |
| Pelkät oikeat vastaukset. | 0 p. |
B1-osa
5. Koulutuspäivä 12 p.
Ohjelmistoyhtiö järjestää koulutuspäivän, jonka tilavuokrat ovat 1 000 euroa. Osallistumismaksu on 30 euroa, joka sisältää ruokailun koulutuspäivän lopuksi. Ruokailun järjestäminen maksaa ohjelmistoyhtiölle 11,50 euroa jokaista ruokailijaa kohti, mutta järjestäjät arvioivat, että puolet osallistujista lähtee kotiin heti koulutuksen päätyttyä eikä osallistu ruokailuun. Kuinka monta osallistujaa koulutuspäivään pitäisi saada, jotta se ei tuottaisi tappiota ohjelmistoyhtiölle? Vastaa kysymykseen muodostamalla ongelmaa kuvaava yhtälö tai epäyhtälö ja ratkaisemalla se. Tehtävässä ei huomioida veroja.
| Esitelty muuttuja (x) selkeästi. | 1 p. |
| Idea: Tuloja tulee 30 kertaa osallistujamäärä. | (1 p.) |
| Tällöin saadaan 30x euroa. Voi käydä ilmi vasta yhtälöstä. | 1 p. |
| Idea: Vain puolet ruokailevat. | (1 p.) |
| Ruokailu maksaa 11\mathrm{,}5 kertaa x/2 euroa TAI 5\mathrm{,}75 kertaa x. Voi käydä ilmi vasta yhtälöstä. | 2 p. |
| Idea: Kuluina huomioitu tilavuokra ja osallistujien ruokailut, tuottona osallistumismaksut. Jälkimmäiset kaksi riippuvat osallistujien määrästä. | (1 p.) |
| Edellisen rivin ideaa vastaava (epä)yhtälö muodostettu: 1000+11\mathrm{,}50\cdot \frac{x}{2}=30x. (Täysin oikea idea: 2 p., oikeahko idea: 1 p.) | 2 p. |
| Johtopäätöksenä: Tehtävänantoa vastaava omilla luvuilla oikein muodostettu (epä)yhtälö ratkaistu, x \approx 41{,}2. | 2 p. |
| riippumaton (Epä)yhtälön ratkaisemisen seurauksena saatu vastaus pyöristetty ylöspäin. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Kaikki syövät: max 1+1+1+0+0+1+1+0+1 = 6. | 6 p. |
| Ilman (epä)yhtälöä, puolet syövät: max 0+1+0+1+0+1+0+0+0 = 3. | 3 p. |
| Ilman (epä)yhtälöä, kaikki syövät: max 0+1+0+0+0+1+0+0+0 = 2. | 2 p. |
| Yhtälönmuodostuksessa on merkkivirhe, joka ei ole ilmeinen painovirhe (esimerkiksi selitysten tai muiden vaiheiden perusteella): 1+1+1+1+2+0+0+0+1 | max 7 p. |
| Muuttujan esittely, pelkkä yhtälö ilman selityksiä ja vastaus. Tavallisten yleisvähennysten mukaan selitysten puutteesta. -1 p. | max 11 p. |
| Vaaditaan yhden euron voitto tai vastaava, -1 p. riviltä 7. | |
| Rivillä 6 ei ole oikeaa ideaa, jos ruokailu on yksi vakio 11,5. | |
| Ratkaistu kumpikin, sekä ''kaikki syövät'' että ''puolet syövät'' ja selitetty, mitä tilanteita nämä vastaavat. Annetaan pisteet ''puolet syövät'' -tavan mukaan, mutta vähennetään 1 piste ylimääräisistä teksteistä. |
6. Puun hinta 12 p.
Taulukossa on esitetty loppuvuonna 2022 raakapuusta harvennushakkuun yhteydessä maksetun kuutiohinnan keskiarvoja eri alueilla.
Mikolla on mäntyä kasvava metsäpalsta Etelä-Suomessa ja Maijulla kuusta kasvava palsta Kainuussa. Mikon palstalta hakattiin harvennushakkuussa noin 110 kuutiometriä puuta, josta 40 % oli tukkipuuta ja 60 % kuitupuuta. Maijun palstalta hakattiin harvennuksessa noin 120 kuutiometriä puuta, josta 70 % oli tukkipuuta ja 30 % kuitupuuta. Kuinka paljon Mikolle ja Maijulle maksettiin hakkuista, kun puun ostaja maksoi heille puun hinnan lisäksi 24 %:n arvonlisäveron?
| Mikon palstalta saatiin 0\mathrm{,}4\cdot 110=44 kuutiota tukkipuuta | 1 p. |
| ja 0\mathrm{,}6\cdot 110=66 kuutiota kuitupuuta. | 1 p. |
| Mikon veroton myyntitulo on 44\cdot 64\mathrm{,}16+66\cdot 20\mathrm{,}63=2823{,}04+1361{,}58=4184{,}62 (laskun rakenne oikein (1 p.) ja luvut oikein (1 p.) (ei vähennystä periytyneestä virheestä)). | 2 p. |
| Miko sai siis 1\mathrm{,}24\cdot 4184{,}62\approx 5188\mathrm{,}93\approx 5200 (euroa) (ALV 1 p., pyöristys 1 p.) | 2 p. |
| Maijun palstalta saatiin 0\mathrm{,}7\cdot 120=84 kuutiota tukkipuuta | 1 p. |
| ja 0\mathrm{,}3\cdot 120=36 kuutiota kuitupuuta. | 1 p. |
| Maijun veroton myyntitulo on 84\cdot 54\mathrm{,}48+36\cdot 17\mathrm{,}61=4576{,}32+633{,}96=5210{,}28 (laskun rakenne oikein (1 p.) ja luvut oikein (1 p.) (ei vähennystä periytyneestä virheestä)). | 2 p. |
| Maiju sai siis 1\mathrm{,}24\cdot 5210{,}28\approx 6460\mathrm{,}75\approx 6500 (euroa) (ALV 1 p., pyöristys 1 p.) | 2 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Vastauksissa hyväksytään tarkkuudet kahdella ja kolmella merkitsevällä numerolla, siis myös 5190 euroa ja 6460 euroa. | |
| Molemmat vastaukset annettu väärällä tarkkuudella, yhteensä | –1 p. |
| Laskettu rahasummat lopuksi yhteen. | –0 p. |
| Lopussa poistettu ALV oikein, eli jaettu luvulla 1\mathrm{,}24. | max 12 p. |
| ALV:tä ei ole käsitelty ollenkaan: 1+1+2+1+1+1+2+1. | max 10 p. |
| Luvut 44, 66, 84, 36 ilmestyneet tyhjästä: Käytetään yleisvähennystä selitysten puutteesta. |
7. Tiimalasi 12 p.
Tiimalasi koostuu kahdesta samanlaisesta osasta, jotka on asetettu vastakkain; katso esimerkki kuvassa . Yhden osan korkeus on 18 cm. Tiimalasi sisältää nestettä, joka valuu hitaasti yläosasta alaosaan. Nestettä on sen verran, että tiimalasin alaosa on täynnä nestettä, kun yläosa on tyhjentynyt.
Tiimalasi käännetään, kun kaikki neste on alaosassa. Kääntämisestä kulunut aika t minuutteina voidaan laskea kaavalla
t =120 [1- (1 -h/18)^3],
jossa h on (uudessa) alaosassa olevan nesteen pinnan korkeus senttimetreinä pohjasta mitattuna.
Millä korkeudella tiimalasin pohjalla olevan nesteen pinta on, kun aikaa kääntämisestä on kulunut tasan tunti? (4 p.)
Kun aikaa on kulunut 13 minuuttia, niin tiimalasin pohjalla on 1,0 desilitraa nestettä. Tiedetään, että tiimalasin pohjalla olevan nesteen määrä on suoraan verrannollinen kääntämisestä kuluneeseen aikaan. Kuinka paljon nestettä tiimalasissa kaiken kaikkiaan on? (8 p.)
| Yhtälö 60=120\left(1-\left(1-\frac{h}{18}\right)^3\right) muodostettu oikein. | 2 p. |
| (Oma oikeanmuotoinen yhtälö ratkaistu oikein ja saatu esimerkiksi) h\approx 3\mathrm{,}7\ (\textrm{cm}). | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Yhtälöä ei muodostettu, arvattu h\approx 3\mathrm{,}7 (tai tarkempi) ja tarkistettu (joko 0 tai 2 pistettä) sekä pyöristetty ainakin yksi merkitsevä numero heikompaan tarkkuuteen ja vastaus on 4 tai 3\mathrm{,}7 tai 3\mathrm{,}71 (1 p.). | max 3 p. |
| Toteamus 1h = 60 min. | + 0 p. |
| Jos yhtälön ratkaisu on virheellinen, mutta oikeansuuntainen, niin toiselta riviltä | 1 p. |
| Tiimalasi on tyhjentynyt täysin, kun h=18. | (1 p.) |
| Parametrin h arvo sijoitettu ajan lausekkeeseen ja laskettu aika 120 min: 120\left(1-\left(1-\frac{18}{18}\right)^3\right)=120 | 2 p. |
| Muodostettu oikea verrantoyhtälö \frac{13}{1}=\frac{120}{V} TAI yhtälö 13V=120 TAI (\frac{120}{13} (2 p.) ja selitys (1 p.)). | 3 p. |
| Saatu vastaus V\approx 9{,}2 (dl) (vastaus ja pyöristys). (Jos vastaus on desilitroina, niin yksikköä ei vaadita.) | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Jos ajan arvoa 120 min ei ole perusteltu lainkaan, eikä h näy missään, pisteet osatehtävän 2 kahdelta ensimmäiseltä riviltä (0+1). | 1 p. |
| Jos aika on laskettu virheellisellä h:n arvolla, osatehtävän 2 kahdelta ensimmäiseltä riviltä (0+1). | 1 p. |
| Jos verranto on väärin, niin ei pisteitä kahdelta viimeiseltä riviltä. | |
| Kolmannen rivin verrantoyhtälö on oikea, jos se on muodostettu oikealla logiikalla, mutta mahdollisesti edellisillä kahdella rivillä saaduilla väärillä lukuarvoilla. Se ei kuitenkaan ole oikea, jos se on esimerkiksi muotoa \frac{13}{1}=\frac{V}{120} tai on esimerkiksi oletettu, että aika ja nesteen korkeus ovat suoraan verrannolliset. |
8. Vitamiinipitoisuus 12 p.
Yritys valmistaa D3-vitamiinikapseleita. Pakkauksen mukaan yksi kapseli sisältää 50 mikrogrammaa D3-vitamiinia. Yritys antaa kapseleiden laadunvarmistuksen erään tutkimuslaitoksen tehtäväksi. Laitoksen mikrobiologi määrittää yhden kapselin sisältämän D3-vitamiinin määrän olevan normaalijakautunut odotusarvona 54,1 mikrogrammaa ja keskihajontana 8,4 mikrogrammaa.
Vitamiinin käyttäjä valitsee pakkauksesta umpimähkään yhden kapselin. Millä todennäköisyydellä kapseli sisältää vähintään 50 mikrogrammaa D3-vitamiinia? (5 p.)
Yritys haluaa varmistaa, että 95 % kapseleista sisältää vähintään 50 mikrogrammaa D3-vitamiinia. Millä D3-vitamiinimäärän odotusarvolla tämä vaatimus saavutetaan laadunvarmistuksessa? Oletetaan, että vitamiinin määrän kasvattaminen ei vaikuta keskihajontaan. (7 p.)
| Valittu komento, jolla käsitellään normaalijakaumaa. | 1 p. |
| Seuraavat pisteet voi saada vain, jos käsittelee normaalijakaumaa. | |
| Sijoitettu keskiarvo 54{,}1 ja keskihajonta 8{,}4. | 1+1 p. |
| Valittu oikea väli X \ge 50. | 1 p. |
| Poimittu vastaus ja saatu täsmälleen 68,7 %. | 1 p. |
| Ratkaistu kokeilemalla (yksi kuva riittää). | |
| Kokeilulla on saatu arvo, joka on välillä 63{,}5–64{,}0 ja todennäköisyys kahden desimaalin tarkkuudella 0{,}95. | 2 p. |
| Poimittu vastaus. | 1 p. |
| Kokeilu riittävän tarkka: Saatu arvo 63{,}82 tai tarkempi TAI todettu, että 63{,}8 antaa alle 0{,}95 ja arvo 63{,}9 antaa yli 0{,}95 TAI todennäköisyydellä 0{,}95 todettu arvo 63{,}8 antaa rajaksi alle 50 ja arvo 63{,}9 antaa rajaksi yli 50 (vain 0 tai 2 pistettä). | 2 p. |
| Vastaus on täsmälleen 63,8 TAI selitettynä täsmälleen 63,9. | 1 p. |
| Perusteltu, miksi muita ratkaisuja ei ole. | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Väli väärin päin (X \leqslant 50): odotusarvon väli 36–36{,}5, tarkka 36{,}18: (1+1+2+0+1) | max 5 p. |
| Osatehtävissä 1 ja 2 on sama virheellinen hajonta: (2, jos todennäköisyysehto toteutuu +1+0+0+1) | max 4 p. |
| TAI ratkaistu suoralla laskulla | |
| Laskettu P(40{,}28323) = 0{,}95. | 1 p. |
| Laskettu poikkeama keskiarvosta 50-40{,}28323 = 9{,}7168. | 3 p. |
| Tehty siirto 54{,}1 + 9{,}7168 (\approx 63{,}8). | 2 p. |
| Vastaus on täsmälleen 63,8 TAI selitettynä täsmälleen 63,9. | 1 p. |
| TAI ratkaisu yhtälöllä | |
| Yhtälön rakentamisessa on oikea idea. | 2 p. |
| Sijoitettu arvot (8{,}4, 50, 0{,}95) oikein. | 3 p. |
| Ratkaistu yhtälö. | 1 p. |
| Vastaus on täsmälleen 63,8 TAI selitettynä täsmälleen 63,9. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Jos ratkaisussa on käytetty normaalijakauman taulukkoa, niin riittää tarkastella asiaa taulukon antamalla tarkkuudella. |
9. Funktion muutosnopeus 12 p.
Tarkastellaan polynomifunktiota p(x) =x^3 +2 x^2 -11 x -1.
Osoita laskulla, että välillä 0 <= x <= 3 funktion p keskimääräinen muutosnopeus on 4. (4 p.)
Määritä väliltä 0 <= x <= 3 kaikki sellaiset kohdat, joissa funktion p hetkellinen muutosnopeus on yhtä suuri kuin keskimääräinen muutosnopeus 4. (8 p.)
| Koska p(3)=11 ja p(0)=-1, | 2 p. |
| saadaan keskimääräiseksi muutosnopeudeksi \frac{p(3)-p(0)}{3-0}=\frac{11-(-1)}{3-0}=4. | 2 p. |
| p'(x)=3x^2+4x-11 (yksi termi oikein 1 p., vain yksi termi väärin 2 p.). | 3 p. |
| Hetkellinen muutosnopeus on sama kuin derivaatta. | (1 p.) |
| STOP: Alla olevia pisteitä vain, jos derivaatta on 2. asteen polynomifunktio. | |
| Ratkaistaan yhtälö p'(x)=4 omaa derivaattaa käyttämällä TAI ratkaistaan, milloin tangentin kulmakerroin on 4. | 1 p. |
| (Esimerkiksi Solve-komennolla saadaan) x=-3 tai x=\frac{5}{3} (likiarvo käy). | 2 p. |
| Näistä annetulla välillä on x= täsmälleen \frac{5}{3}. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Derivaatta voi olla laskettu kohdassa 1. | |
| Haettu ohjelmistolla kokeilemalla, milloin tangentin kulmakerroin on neljä, ja saatu: (x\approx 1{,}67 ja kokeilu välillä [0,3]) TAI (x=-3 ja x\approx 1{,}67) (0+1+1+2+0) | max 4 p. |
| Toiseksi viimeiseltä riviltä ei pisteitä, jos ratkaistu muu yhtälö kuin p'(x)=4 (poislukien selvät painovirheet). | |
| Alkupiste: Ymmärretty, että derivaatta on hyödyllinen tässä tehtävässä. | 1 p. |
B2-osa
10. Oppilaan ratkaisutapa 12 p.
Oppilas kertoo keksineensä helpon tavan laskea murtolukujen jakolaskun: ''Jaan osoittajat keskenään ja nimittäjät keskenään, jolloin saan suoraan vastauksen murtolukuna.'' Esimerkkinä hän mainitsee
(3/20) /(1/4) =(3/1) /(20/4) =3/5.
Onko esimerkkilaskun lopputulos oikein? (2 p.)
Laske oppilaan menetelmällä \frac6{35} : \frac35. (4 p.)
Keksi esimerkki, jossa ratkaisutapa tuottaa lopputuloksena murtoluvun, joka ei ole supistetussa muodossa. (6 p.)
Tässä murtoluku on muotoa n/m tai -n/m oleva merkintä, jossa n on luonnollinen luku ja m on positiivinen kokonaisluku.
| \frac{3}{20} : \frac{1}{4} = \frac{3}{20} \cdot \frac{4}{1} TAI \frac{3}{20} : \frac{1}{4} = \frac{12}{20} TAI laskimella \frac{3}{20} : \frac{1}{4} = 0{,}6 \left(= \frac{3}{5}\right) | 1 p. |
| = \frac{12}{20}, joten lopputulos on oikein TAI = \frac{3}{5} (, joten lopputulos on oikein). | 1 p. |
| \left(\frac{6}{35} : \frac{3}{5} =\right) \frac{6:3}{35:5}, osoittaja 1 p. + nimittäjä 1 p. (omilla murtoluvuilla) | 2 p. |
| täsmälleen = \frac{2}{7} | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Ei ole käytetty tehtävässä esitettyä ratkaisutapaa (tai ratkaisutapa ei käy ilmi). | 0 p. |
| Kopiointivirhe (2+0). | max 2 p. |
| Murtolukujen jakolaskulla tarkoitetaan merkintää \pm \frac{n_1}{m_1} : \pm\frac{n_2}{m_2} (tai vastaavaa), missä n_1 on luonnollinen luku ja n_2, m_1 ja m_2 ovat positiivisia kokonaislukuja. Murtolukujen jakolasku on toimiva (tehtävänannon kannalta), jos n_1/n_2=a on kokonaisluku, m_1/m_2=b on kokonaisluku ja kokonaisluvuilla a ja b on yhteisiä tekijöitä. |
| Annettu tehtävänannon määritelmän mukaisten murtolukujen jakolasku, joka on eri kuin tehtävänannossa. | 1 p. |
| riippumaton Todettu tai osoitettu, että laskun tulos ei ole supistetussa muodossa, tai tehty supistus. (Tämä piste koskee laskun lopputulosta, myös mahdollisesti virheellisillä laskuilla tullutta, kunhan alkuperäisten lukujen osoittajat ja nimittäjät ovat kokonaislukuja.) | 1 p. |
| STOP: Seuraavat pisteet voi saada vain, jos esimerkkilukujen osoittajat ja nimittäjät ovat kokonaislukuja, ja niiden jakolasku on toimiva. | |
| Annettu murtolukujen jakolasku on toimiva. | 1 p. |
| Johtopäätöksenä = \pm \frac{n_1: n_2}{m_1 : m_2} | (1+1 p.) |
| Johtopäätöksenä = \pm \frac{a}{b} (suoritettu jakolaskut) | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Annetussa esimerkkiluvussa osoittaja ja/tai nimittäjä on negatiivinen kokonaisluku (0+1+1+2+1). | max 5 p. |
| Ei ole käytetty tehtävässä esitettyä ratkaisutapaa, mutta pari on toimiva (1+1+1+0+0). | max 3 p. |
| Esimerkkejä: Supistamaton muoto: \frac{8}{4}, \frac{0}{2}. Supistettu muoto: \frac{3}{4}, \frac{3}{1}, \frac{1}{1} ja \frac{0}{1}. |
11. Maitotölkki 12 p.
Maitotölkki voidaan mallintaa suorakulmaisena särmiönä ja sen päällä olevana yläosana. Oletetaan, että täydessä maitotölkissä maito täyttää täsmälleen särmiöosan.
Sekä litran että 1,75 litran maitotölkin pohja on neliö ja särmiöosan korkeus on 20 cm. Määritä kummassakin tapauksessa pohjaneliön sivun pituus. (4 p.)
Arvioidaan pakkauksen materiaalin määrää kaavalla A_1 +4,5 *A_2, missä A_1 on särmiön sivutahkojen yhteenlaskettu pinta-ala ja A_2 on pohjaneliön pinta-ala. Kummassa maitotölkissä on enemmän pakkausmateriaalia suhteessa maidon määrään? (8 p.)
| Suuremman maitotölkin pohjan ala on \frac{1\mathrm{,}75 \text{ dm}^3}{2\text{ dm}} =0\mathrm{,}875\, \textrm{dm}^2, | 1 p. |
| joten sen pohjaneliön sivun pituus on \sqrt{0\mathrm{,}875\text{ dm}^2}=0{,}935414\ldots \text{ dm} \approx 0\mathrm{,}94\, \textrm{dm}=9{,}4\, \textrm{cm}. | 1 p. |
| Pienemmän maitotölkin pohjan ala on \frac{1 \text{ dm}^3}{2\text{ dm}} =0\mathrm{,}5\, \textrm{dm}^2, | 1 p. |
| joten sen pohjaneliön sivun pituus on \sqrt{0\mathrm{,}5 \text{ dm}^2}=0{,}707107\ldots \text{ dm}\approx 0\mathrm{,}71 \text{ dm}= 7{,}1\, \textrm{cm}. | 1 p. |
| TAI | |
| Muodostettu oikeat yhtälöt, joissa yksiköt jotenkin huomioitu (esimerkiksi 1000 = x^2 \cdot 20, 1=x^2\cdot2 tai 1 \textrm{l}= x^2 \cdot 20 \textrm{ cm} ja niin edelleen.) | 2 p. |
| Ratkaistu yhtälöistä oikeat sivunpituudet (käsin tai ohjelmistolla). | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Vastauksessa kelpaa 1, 2 tai 3 numeron tarkkuus. | |
| Yksikönmuunnosvirhe TAI yksiköt huomioimatta: -1 p./tölkki | |
| Alkupiste: Yhteensopiva yksikkömuunnos, esimerkiksi korkeus 2 dm ja tilavuus 1 dm^3 tai korkeus 20 cm ja tilavuus 1000 cm^3. | 1 p. |
| Arvattu vastaus ainakin kahden merkitsevän numeron tarkkuudella oikein ja tarkistettu: 1 p./tölkki | max 2 p. |
| Laskettu jommankumman tölkin sivutahkon pinta-ala | (1 p.) |
| Suuremman tölkin sivujen ala yhteensä 4\cdot 2\cdot 0\mathrm{,}935\ldots \, \textrm{dm}^2=7{,}483... \text{ dm}^2. | 1 p. |
| Materiaalia tarvitaan siis (4\mathrm{,}5\cdot 0\mathrm{,}875+4\cdot 2\cdot 0\mathrm{,}935 \ldots )\, \textrm{dm}^2=11{,}420\ldots \text{ dm}^2. | 1 p. |
| Suhde on \frac{(4\mathrm{,}5\cdot0\mathrm{,}875+4\cdot 2\cdot 0\mathrm{,}935\ldots )\, \textrm{dm}^2}{1\mathrm{,}75\mathrm{l}}\approx 6\mathrm{,}526\ldots \, \frac{\textrm{dm}^2}{\mathrm{l}}. | 1 p. |
| Vastaavasti pienemmän tölkin sivujen ala yhteensä 4\cdot 2\cdot 0\mathrm{,}707\ldots \, \textrm{dm}^2=5{,}656... \text{ dm}^2. | 1 p. |
| Materiaalia tarvitaan siis (4\mathrm{,}5\cdot0\mathrm{,}5+4\cdot 2\cdot 0\mathrm{,}707\ldots )\, \textrm{dm}^2=7{,}906\ldots \text{ dm}^2. | 1 p. |
| Suhde on \frac{(4\mathrm{,}5\cdot0\mathrm{,}5+4\cdot 2\cdot 0\mathrm{,}707 \ldots )\, \textrm{dm}^2}{1\mathrm{l}}\approx 7\mathrm{,}906\ldots \, \frac{\textrm{dm}^2}{\mathrm{l}}. | 1 p. |
| Rivien 4 ja 7 Johtopäätöksenä Pienemmässä tölkissä on enemmän materiaalia suhteessa maidon määrään. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Osatehtävästä 1 periytyvä virhe | max 8 p. |
| Rivien 4 ja 7 pisteet voi saada laskemalla mitkä tahansa suhteet, joista loppupäätelmän voi tehdä. | |
| Jos unohtaa kertoa sivutahkon pinta-alan neljällä, vähennetään 1 p./tölkki (rivit 2 ja 5), mutta pisteitä voi vielä saada alemmista riveistä. | |
| Systemaattinen pieni virhe, joka toistuu kummallakin tölkillä: vähennys vain toisesta tölkistä. | |
| Välivaiheet vähintään kahden merkitsevän numeron tarkkuudella. Muuten -1 p. koko osatehtävästä. |
12. Todennäköisyyslaskennan alkuperä 12 p.
Todennäköisyyslaskenta sai alkunsa 1600-luvun Ranskasta, jossa eräissä piireissä harjoitettiin uhkapeliä. Antoine Gombaud oli ranskalainen kirjailija ja peluri, joka huomasi, että voiton todennäköisyys oli eri kahdessa noppapelissä, mutta hän ei pystynyt perustelemaan tätä matemaattisesti. Koska Gombaud käytti myös nimeä Chevalier de Méré, tätä kutsutaan de Mérén ongelmaksi. Pelien periaatteet ovat seuraavat:
Kummassakin pelissä haastaja pelasi de Méréä vastaan. Sekä haastaja että de Méré laittoivat pottiin saman verran rahaa, ja voittaja sai koko potin.
Ensimmäisessä pelissä de Méré heitti yhtä noppaa neljä kertaa. Jos hän sai vähintään yhden kuutosen, hän voitti, muussa tapauksessa hän hävisi. Kokemus osoitti, että tämä oli de Mérélle tuottoisa peli.
Toisessa pelissä de Méré heitti kahta noppaa yhtä aikaa 24 kertaa. Jos hän sai vähintään yhden kuutosparin, hän voitti, muussa tapauksessa hän hävisi. Tämä peli osoittautui kuitenkin tappiolliseksi de Mérélle.
Vastatakseen de Mérén ongelmaan kaksi aikalaismatemaatikkoa, Blaise Pascal ja Pierre de Fermat, kehittivät todennäköisyyslaskennan teorian alkeet ja osoittivat, että pitkällä aikavälillä de Méré voittaa ensimmäisessä pelissä ja häviää toisessa. Osoita tämä todennäköisyyslaskennan keinoin.
| 1. peli | |
| Todennäköisyys, ettei saada yhtään kuutosta neljällä heitolla, on \left(\frac{5}{6}\right)^4 (lauseke muotoa x^y, missä x on todennäköisyys ja y >1, y\in \mathbb{N}; \frac{5}{6}; potenssi 4), | 1+1+1 p. |
| joten de Mérén voittotodennäköisyys ensimmäisessä pelissä on komplementtitodennäköisyyden perusteella 1-\left(\frac{5}{6}\right)^4=\frac{671}{1296}\approx 0\mathrm{,}52. (Idea komplementista (1 p.). Toinen piste vain, jos ensimmäiseltä riviltä vähintään 2 p.) | 2 p. |
| Täten melko täsmälleen 0\mathrm{,}52>0\mathrm{,}5 TAI johtopäätös sanallisesti. | 1 p. |
| TAI Binomikertoimien avulla | |
| Lasketaan todennäköisyydet P(1\ \text{kertaa}\ 6), P(2\ \text{kertaa}\ 6),\ P(3\ \text{kertaa}\ 6),\ P(4\ \text{kertaa}\ 6) esimerkiksi kombinaatioiden avulla: \binom{4}{1} \left( \frac{1}{6} \right)\left(\frac{5}{6}\right)^3,\ \binom{4}{2} \left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^2,\ \binom{4}{3} \left(\frac{1}{6}\right)^3\left(\frac{5}{6}\right),\ \binom{4}{4} \left(\frac{1}{6}\right)^4\left(\frac{5}{6}\right)^0. | |
| (tunnistettava binomitodennäköisyyden lauseke 1 p., yksi termi oikein 2 p., kolme termiä oikein 3 p., neljä termiä oikein, eikä ylimääräisiä 4 p.) | 4 p. |
| Lasketaan 2–4 todennäköisyyden summa, ja näistä vähintään kaksi on oikein. Tulos on välillä (0, 1). (\frac{671}{1296}\approx 0\mathrm{,}52) | 1 p. |
| Täten melko täsmälleen 0\mathrm{,}52>0\mathrm{,}5 TAI johtopäätös sanallisesti. | 1 p. |
| TAI Binomijakaumatyökalulla | |
| Käytetään binomityökalua tai vastaavia komentoja. | 1 p. |
| Johtopäätöksenä Sijoitettu n= 4 ja p=\frac16 (likiarvo käy) binomityökaluun. | 1+1 p. |
| Valittu binomityökaluun oikea väli (1\le X) tai alaraja. | 1 p. |
| Saatu todennäköisyys 0{,}52. | 1 p. |
| Täten melko täsmälleen 0\mathrm{,}52>0\mathrm{,}5 TAI johtopäätös sanallisesti. | 1 p. |
| 2. peli | |
| Todennäköisyys, ettei saada yhtään kuutosparia 24 heitolla, on \left(\frac{35}{36}\right)^{24}, sillä erilaisia heittopareja on 36 kappaletta. (osoittaja 35, nimittäjä 36, potenssi 24) | 1+1+1 p. |
| Siten de Mérén voittotodennäköisyys toisessa pelissä on komplementtitodennäköisyyden perusteella 1-\left(\frac{35}{36}\right)^{24}\approx 0\mathrm{,}49. (Idea komplementistä (1 p.). Toinen piste vain jos ensimmäiseltä riviltä vähintään 2 p.) | 2 p. |
| Täten melko täsmälleen 0\mathrm{,}49<0\mathrm{,}5 TAI johtopäätös sanallisesti. | 1 p. |
| TAI Binomijakaumatyökalulla | |
| Käytetään binomityökalua tai vastaavia komentoja. | 1 p. |
| Johtopäätöksenä Sijoitettu n= 24 ja p=\frac1{36} (likiarvo käy) binomityökaluun. | 1+1 p. |
| Valittu binomityökaluun oikea väli (1\le X) ja saatu todennäköisyys 0{,} 49. | 2 p. |
| Täten melko täsmälleen 0\mathrm{,}49<0\mathrm{,}5 TAI johtopäätös sanallisesti. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Kaikki tarkkuudet, joilla voi tehdä vertailun, hyväksytään. | |
| Puutteelliset selitykset -1 p./peli, kummankin pelin toisesta pisteestä alkaen. Myös binomityökaluratkaisut tai muut vastaavat vaativat selityksen. Tällöin selityksen tulee sitoa kuvakaappaus ja tehtävän tilanne yhteen. | |
| Sulkeet puuttuvat murtolukupotenssista, mutta laskettu oikein: Yleisvähennys huonoista merkinnöistä -1 p. koko tehtävästä. |
13. Derivoiva avaruusluotain 12 p.
Avaruusluotain mittaa planeetan lämpötilaa. Sen piti lähettää tietoa lämpötilasta funktiona T(t) aikavälillä 0 <= t <= 9. Ohjelmistovirheen takia saatiin kuitenkin vain tieto, että funktion derivaatta T’(t) on negatiivinen, kun t < 2, positiivinen, kun 2 < t < 4, ja jälleen negatiivinen, kun t > 4. Tutkijat miettivät, mitä tämän perusteella voidaan sanoa lämpötilasta T.
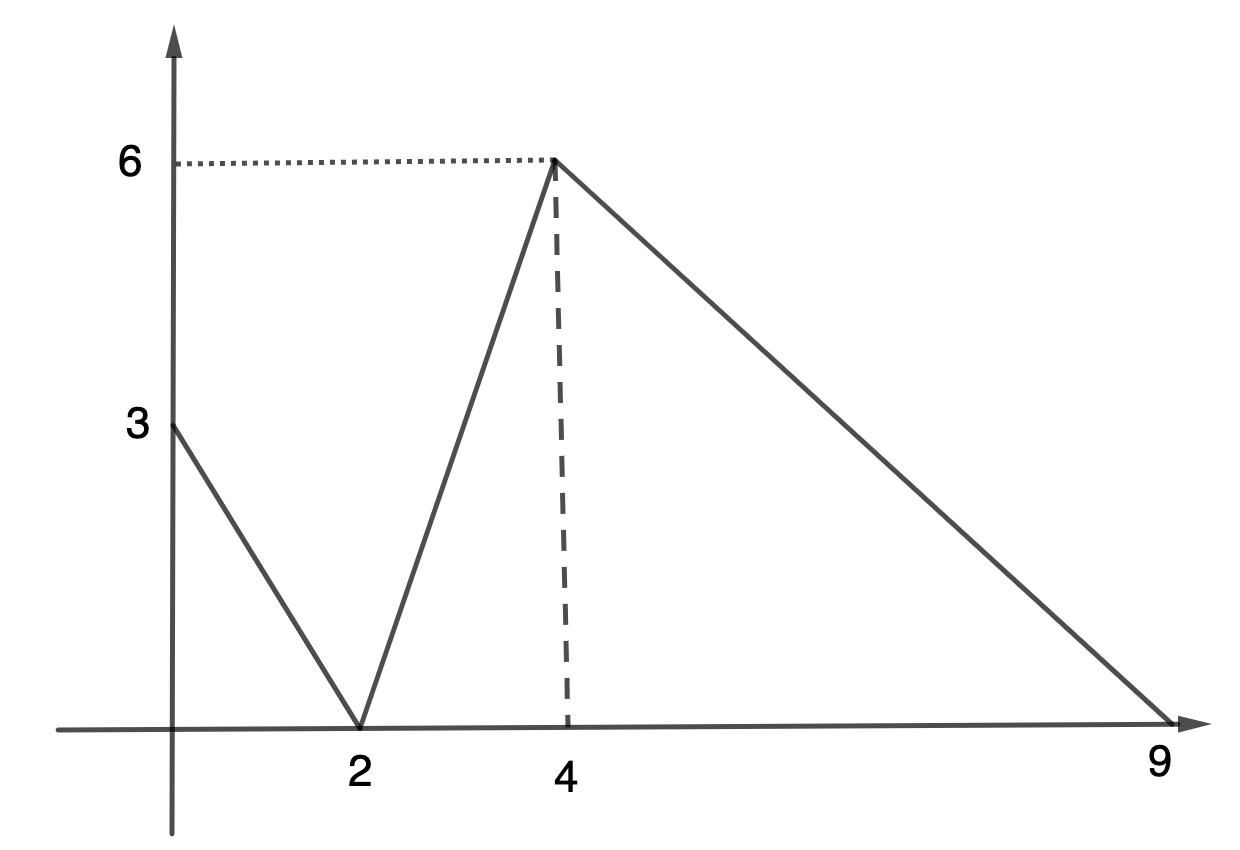
Hahmottele esimerkki lämpötilafunktion T kuvaajasta, jolla on lisäksi se ominaisuus, että lämpötilan suurin arvo saavutetaan hetkellä t =4. (6 p.)
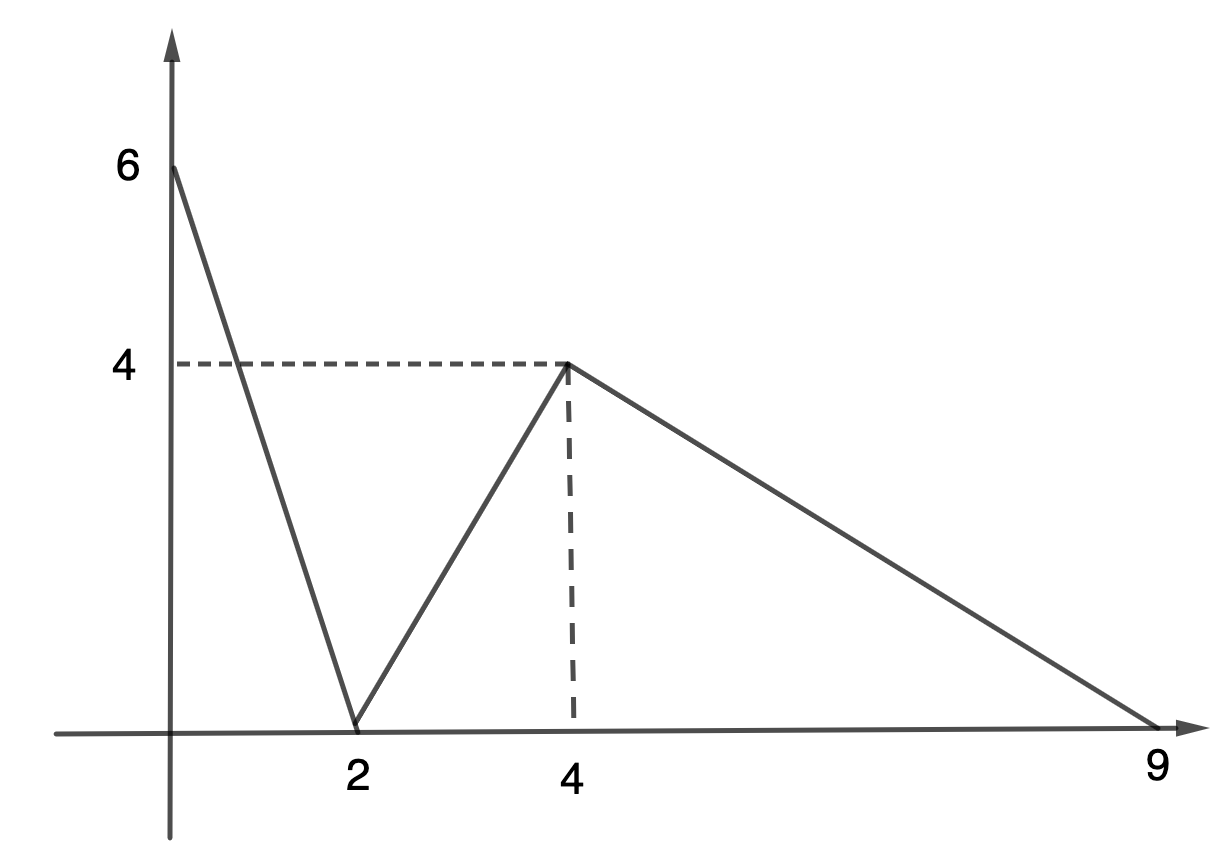
Hahmottele esimerkki lämpötilafunktion T kuvaajasta, jolla on lisäksi se ominaisuus, että lämpötilan suurinta arvoa ei saavuteta hetkellä t =4. (6 p.)
Selitä kummassakin tapauksessa sanallisesti, miten vaaditut lämpötilafunktion ominaisuudet näkyvät kuvaajassa.
| Kuva | |
| Kuvaaja on jatkuva ja piirtotarkkuuden rajoissa "derivoituvan näköinen", mahdollisesti ajanhetkiä t=0, 2, 4, 9 lukuun ottamatta. | |
| STOP: Alla olevia pisteitä voi saada vain, jos yllä olevat ehdot toteutuvat. | |
| Monotoninen oikealla tavalla oikeilla lukuväleillä. | 1 p. |
| Edellisen täyttyessä: suurin arvo on hetkellä t=4. | 3 p. |
| Sanallinen selitys: derivaatan yhteys vähenevyyteen/kasvavuuteen + huomattu, että globaali maksimi kohdassa t=4. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kuvaaja ei ole oikealla välillä, mutta ainakin välillä [1,5] | –1 p. |
| Jos kuvaaja on piirretty laajemmalle välille, niin edellisen kohdan mukainen -1 p., ja muuten arvioinnissa tarkastellaan vain väliä [0,9]. | |
| Sanallisista selityksistä saa pisteitä vain, jos selitetyt asiat näkyvät myös kuvassa. Huomaa, että esimerkiksi paraabeli, jolla on huippu pisteessä t=4, voi antaa mahdollisuuden yhteen selityspisteeseen, mutta ei yhteenkään kuvapisteeseen. | |
| Kulkukaavio yksinään ei anna pisteitä, mutta kulkukaavio kuvan yhteydessä voi antaa selityspisteen. | |
| Esimerkki kuvaajasta: |
| Kuva | |
| Kuvaaja jatkuva ja piirtotarkkuuden rajoissa "derivoituvan näköinen", mahdollisesti ajanhetkiä t=0, 2, 4, 9 lukuun ottamatta. | |
| STOP: Alla olevia pisteitä voi saada vain, jos yllä olevat ehdot toteutuvat. | |
| Monotoninen oikealla tavalla oikeilla lukuväleillä. | 1 p. |
| Edellisen täyttyessä: Maksimi ei ole kohdassa t=4. | 3 p. |
| Sanallinen selitys: derivaatan yhteys vähenevyyteen/kasvavuuteen (voi viitata edelliseen kohtaan) + huomattu globaali maksimi ei ole kohdassa t=4. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kuvaaja ei ole oikealla välillä, mutta ainakin välillä [1,5] | –1 p. |
| Jos kuvaaja on piirretty laajemmalle välille, niin edellisen kohdan mukainen -1 p, ja muuten arvioinnissa tarkastellaan vain väliä [0,9]. | |
| Sanallisista selityksistä saa pisteitä vain, jos selitetyt asiat näkyvät myös kuvassa. | |
| Kulkukaavio yksinään ei anna pisteitä, mutta kulkukaavio kuvan yhteydessä voi antaa selityspisteen. | |
| Esimerkki kuvaajasta: |