Beskrivningar av goda svar: SV – Matematik, kort lärokurs
20.3.2024
Slutgiltiga beskrivningar av goda svar 14.5.2024
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal i den högra kolumnen för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i parentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- Om inget annat anges, godkänns även en gällande siffra fler eller färre än i anvisningarna.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Ordet STOP betyder att raden beskriver villkor som måste uppfyllas för att kunna få poäng för den fortsatta lösningen.
- Terminologi
- ''Svar räcker'' betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- ''Startpoäng'' betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- ''maxN'' betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- ''Svaret endast som närmevärde'' betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (t.ex. noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (t.ex. e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (t.ex. e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (t.ex. x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (t.ex. parenteser som fattas men korrekt beräknat; =-tecknet använt ''i kedja'', m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Del A
1. Basuppgifter 12 p.
Välj det alternativ som är korrekt. Svaren behöver inte motiveras. Korrekt svar 2 p., fel svar 0 p., inget svar 0 p.
1.1 Vilken är lösningen till ekvationen 3 x -8 =34? 2 p.
- x =14 (2 p.)
1.2 Vilken är den positiva lösningen till ekvationen x^2 -100 =0? 2 p.
- x =10 (2 p.)
1.3 Bestäm den punkt där linjen y=3x+12 skär x-axeln. 2 p.
- x =-4 (2 p.)
1.4 Bestäm den punkt där linjen y +2 x -6 =0 skär y-axeln. 2 p.
- y =6 (2 p.)
1.5 Vad är värdet av funktionen f(x) =3 x^8 -68 i punkten x =2? 2 p.
- f(2) =700 (2 p.)
1.6 Vilken är lösningen till ekvationen x^3 +2197 =0? 2 p.
- x =-13 (2 p.)
2. Vinkeljakt 12 p.
Bestäm de sex obekanta vinklar som är betecknade i figurerna med en grads noggrannhet.
I den här uppgiften ska du endast skriva in de slutliga resultaten av uträkningarna utan mellansteg och motiveringar i svarsfälten. Svaret på varje deluppgift är ett heltal.
2.1 Bestäm vinkeln \alpha. 2 p.
- 60 (2 p.)
2.2 Bestäm vinkeln \beta. 2 p.
- 25 (2 p.)
2.3 Bestäm vinkeln \gamma. 2 p.
- 51 (2 p.)
2.4 Bestäm vinkeln \delta. 2 p.
- 47 (2 p.)
- –47 (1 p.)
- 43 (1 p.)
2.5 Bestäm vinkeln \epsilon. 2 p.
- 24 (2 p.)
2.6 Bestäm vinkeln \zeta. 2 p.
- 62 (2 p.)
3. Ett lån 12 p.
Paul har tagit ett lån på 135 000, vars fasta årsränta är 4,5 procent. Lånets återbetalningstid är 12 år, och det amorteras varje månad. Beräkna Pauls 13:e betalningsrat då det är fråga om ett
annuitetslån. (6 p.)
lån med jämn amortering. (6 p.)
| Månadsräntan 0{,}375\, \% bestämd (möjligen samtidigt som räntekoefficienten bestämts). | 1 p. |
| Räntekoefficienten 1<q<2 beräknad eller angiven, och svarar mot den egna räntan. Denna kan även framgå implicit i annuitetsformeln. | 1 p. |
| Antalet amorteringsrater är 144. Detta kan även framgå implicit. | 1 p. |
| Annuitetsformeln A=Kq^n \frac{1-q}{1-q^n} använd med egen räntekoefficient (1<q<2) och tillhörande antal amorteringar. (rätt antal för månadsbetalningar: q=1\mathrm{,}00375 och n=144 och för årsbetalningar q=1\mathrm{,}045 och n=12). (Antingen 0 p. eller 2 p., bara standardavdrag.) | 2 p. |
| Numeriskt värde och bara denna noggrannhet godkänns exakt 1215,01. | 1 p. |
| Bestämt amorteringsdelen av betalningsraten 135\,000/144 = 937{,}50 (euro). | 2 p. |
| Bestämt den återstående skulden 135\,000-12\cdot 937\mathrm{,}50=123\, 750. (13 amorteringar, 1 p.) | 2 p. |
| Korrekt bestämt betalningsratens ränteandel med de egna numeriska värdena (123\,750\cdot 0\mathrm{,}00375=464\mathrm{,}06). | 1 p. |
| Numeriskt värde och bara denna noggrannhet godkänns exakt 1401,56. | 1 p. |
| Specifika anvisningar för uppgiften | |
| Obs: Om första deluppgiften saknas eller inte innehåller ens försök till att bestämma månadsräntan och antal amorteringar, kan man ge poäng för att ha bestämt månadsräntan och antal amorteringar (1 + 1) baserat på svaret i deluppgift 2, om dessa tal är explicit angivna i deluppgift 2. |
4. Exponentiella grafer 12 p.
Figur består av grafen till funktionen u(x)=a\,b^x. Bestäm konstanterna a och b. (6 p.)
Figur består av graferna f, g och h. Två av dessa utgör inte grafen till en funktion i formen v(x)=c\,d^x oberoende av värdena på konstanterna c och d. Motivera vilka två. (6 p.)
| Två av följande ekvationer: ab^{-1}=0{,}75, ab^0=1{,}5, ab^1=3 och ab^2=6. | 1+1 p. |
| Bestämt a eller b antingen direkt eller genom att kombinera två av ekvationerna. | 2 p. |
| Bestämt det andra värdet. | 2 p. |
| ELLER | |
| Noterat att funktionsvärdet fördubblas då x växer med ett (1 p.) och härur slutit sig till att b=2 (2 p.). | 3 p. |
| Bestämt via skärningen med y-axeln, att a=1{,}5. | 3 p. |
| Specifika anvisningar för deluppgiften | |
| Alla korrekta ekvationer godkänns, om litet fel så -1 p. | |
| Ett av värdena (möjligtvis felaktigt) uppkommit från ingenstans, en ekvation bildats, och det andra värdet beräknats därur eller på annat riktigt sätt. | max 3 p. |
| Gissningslösning: Både a och b rätt (1 p.) + kontroll i en punkt (2 p.) + kontroll i andra punkten (2 p.). | max 5 p. |
| Fel värden och kontroll i en punkt. | 1 p. |
| Om man sätter in värdet a=1{,}5 i ekvationen 6=ab^2 behöver man inte förklara varför b inte kan vara den negativa roten. | |
| Förtydligande: För att få den första radens poäng bör studenten ha läst av motsvarande punkt(er) i koordinatsystemet från kurvan och kombinerat dessa med kurvans ekvation. Att kombinera en punkt med ekvationen ger en poäng och att kombinera två punkter med ekvationen ger två poäng. |
| Grundprincipen är motivering (2 p.) + svar (1 p.). Svarspoängen kräver åtminstone någorlunda god motivering, så 0+1 är inte möjligt. | |
| Exempel på motiveringar för två poäng: | 2 p. |
| Går igenom origo ELLER har ett nollställe ELLER f(x) = 0 ELLER skär x-axeln | |
| Får negativa och positiva värden | |
| h(x) = x + 1 | |
| Jämförelse mellan kvoter (Till exempel \frac{h(1)}{h(0)}=\frac{2}{1}=2 och \frac{h(2)}{h(1)}=\frac{3}{2}\ne 2, så de är inte samma.) | |
| Exempel på motiveringar för ett poäng: | 1 p. |
| Är en linje ELLER linjär ELLER affin | |
| h(x) = ax + b | |
| Grafen går under nollan. | |
| Exempel på motivering som inte ger poäng: | 0 p. |
| Får negativa värden |
| Specifika anvisningar för deluppgiften | |
| Startpoäng: Endast försökt förklara varför g är exponentiell. (Notera att grafen inte räcker för att fastställa detta.) | max 2 p. |
| Endast rätta svar. | 0 p. |
Del B1
5. Utbildningsdag 12 p.
Ett programvaruföretag ordnar en utbildningsdag där hyran för lokalen är 1 000 euro. Deltagaravgiften är 30 euro och den inkluderar en måltid som avslutning på utbildningsdagen. Att arrangera måltiden kostar programvaruföretaget 11,50 euro för varje matgäst, men arrangörerna uppskattar att hälften av deltagarna åker hem direkt efter utbildningen och inte deltar i måltiden. Hur många deltagare borde man få till utbildningsdagen för att den inte ska orsaka en förlust för programvaruföretaget? Besvara frågan genom att bilda en ekvation eller olikhet som beskriver problemet och genom att lösa den. I uppgiften beaktas inte skatter.
| Variabeln (x) tydligt introducerad. | 1 p. |
| Idé: Inkomsterna är 30 gånger deltagarantalet. | (1 p.) |
| Inkomsterna är 30x euro. Kan framgå först i ekvationen. | 1 p. |
| Idé: Bara hälften deltar i måltiden. | (1 p.) |
| Måltiden kostar 11\mathrm{,}5 gånger x/2 euro ELLER 5\mathrm{,}75 gånger x. Kan framgå först i ekvationen. | 2 p. |
| Idé: Lokalhyra och måltider betraktade som utgifter, deltagaravgifter betraktade som inkomster. De två senare beror på antalet deltagare. | (1 p.) |
| En olikhet eller ekvation bildad som svarar mot idén på föregående rad: 1000+11\mathrm{,}50\cdot \frac{x}{2}=30x. (Helt rätt idé: 2 p., någorlunda rätt idé: 1 p.) | 2 p. |
| Som slutsats: Löst en ekvation eller olikhet som svarar mot uppgiftsbeskrivningen, x \approx 41{,}2. | 2 p. |
| oberoende Lösningen till ekvationen avrundad uppåt. | 1 p. |
| Specifika anvisningar för uppgiften | |
| Alla äter: max 1+1+1+0+0+1+1+0+1 = 6. | 6 p. |
| Utan olikhet eller ekvation, hälften äter: max 0+1+0+1+0+1+0+0+0 = 3. | 3 p. |
| Utan olikhet eller ekvation, alla äter: max 0+1+0+0+0+1+0+0+0 = 2. | 2 p. |
| Teckenfel i ekvationen (Gäller ej om det av förklaringar eller andra steg uppenbart framgår att teckenfelet är ett tryckfel): 1+1+1+1+2+0+0+0+1 | max 7 p. |
| Variabeln introducerad, endast ekvation utan förklaring samt svar. Standardavdrag för bristande förklaring tillämpas. -1 p. | max 11 p. |
| Lösningen antar att vinsten måste vara minst en euro, eller liknande, -1 p. från rad 7. | |
| Rad 6 innehåller inte rätt idé om måltidskostnaden är en konstant 11,5. | |
| Löst både fallet ''alla äter'' och ''hälften äter'' och förklarat vilka situationer dessa beskriver: Poäng ges för ''hälften äter'' -lösningen, men 1 poäng dras av för överflödig text. |
6. Virkespriser 12 p.
I tabell presenteras medelvärden av det betalda kubikpriset för råvirke i samband med beståndsvårdande avverkning på olika områden i slutet av år 2022.
Mikael har en skogsparcell i södra Finland där det växer tall och Maj har en parcell i Kajanaland där det växer gran. På Mikaels parcell avverkades cirka 110 kubikmeter virke i en gallring, av vilket 40 % var timmer och 60 % massaved. På Majs parcell avverkades cirka 120 kubikmeter virke i en gallring, av vilket 70 % var timmer och 30 % massaved. Hur mycket pengar fick Mikael och Maj för avverkningarna, då virkesköparen förutom virkespriset betalade mervärdesskatten 24 %?
| Från Mikaels parcell fick man 0\mathrm{,}4\cdot 110=44 kubikmeter timmer | 1 p. |
| och 0\mathrm{,}6\cdot 110=66 kubikmeter massaved. | 1 p. |
| Mikaels skattefria inkomst från försäljningen är 44\cdot 64\mathrm{,}16+66\cdot 20\mathrm{,}63=2823{,}04+1361{,}58=4184{,}62 (strukturen på beräkningen rätt (1 p.) och talen rätt (1 p.) (inget avdrag för fortplantade fel)). | 2 p. |
| Mikael fick alltså 1\mathrm{,}24\cdot 4184{,}62\approx 5188\mathrm{,}93\approx 5200 (euro) (moms 1 p., avrundning 1 p.) | 2 p. |
| Från Majs parcell fick man 0\mathrm{,}7\cdot 120=84 kubikmeter timmer | 1 p. |
| och 0\mathrm{,}3\cdot 120=36 kubikmeter massaved. | 1 p. |
| Majs skattefria inkomst från försäljningen är 84\cdot 54\mathrm{,}48+36\cdot 17\mathrm{,}61=4576{,}32+633{,}96=5210{,}28 (strukturen på beräkningen rätt (1 p.) och talen rätt (1 p.) (inget avdrag för fortplantade fel)). | 2 p. |
| Maj fick alltså 1\mathrm{,}24\cdot 5210{,}28\approx 6460\mathrm{,}75\approx 6500 (euro) (moms 1 p., avrundning 1 p.) | 2 p. |
| Specifika anvisningar för uppgiften | |
| Svar med två eller tre gällande siffrors noggrannhet godkänns, alltså även 5190 euro och 6460 euro. | |
| Båda svaren angivna med fel noggrannhet, totalt | –1 p. |
| Räknat ihop summorna i slutet. | –0 p. |
| I slutet dragit bort momsen, alltså dividerat med 1\mathrm{,}24. | max 12 p. |
| Moms inte behandlad alls: 1+1+2+1+1+1+2+1. | max 10 p. |
| Talen 44, 66, 84, 36 uppstått utan härledning: Standardavdrag för bristfällig förklaring. |
7. Ett timglas 12 p.
Ett timglas består av två likadana delar som placerats mot varandra; se exempel i figur . En del har höjden 18 cm. Timglaset innehåller en vätska som sakta rinner från den övre delen till den nedre delen. Det finns så mycket vätska att timglasets nedre del är fylld med vätska då den övre delen har tömts.
Timglaset vänds då all vätska är i den nedre delen. Den tid t som gått i minuter från det att timglaset vänts kan beräknas med formeln
t=120\left(1-\left(1-\frac{h}{18}\right)^3\right),
där h är höjden på vätskans yta i centimeter mätt från bottnen i (den nya) nedre delen.
På vilken höjd ligger ytan på vätskan på timglasets botten då det gått exakt en timme från att timglaset vänts? (4 p.)
Då det förflutit 13 minuter finns det 1,0 deciliter vätska på timglasets botten. Vi vet att mängden vätska på timglasets botten är direkt proportionell mot den tid som gått sedan vändningen. Hur mycket vätska finns det totalt i timglaset? (8 p.)
| Ekvationen 60=120\left(1-\left(1-\frac{h}{18}\right)^3\right) korrekt bildad. | 2 p. |
| (Korrekt löst egen ekvation med rätt form, och fått exempelvis) h\approx 3\mathrm{,}7\ (\textrm{cm}). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Ingen ekvation bildad, gissat h\approx 3\mathrm{,}7 (eller noggrannare) och kontrollerat (antingen 0 eller 2 poäng), samt avrundat till åtminstone en gällande siffra svagare noggrannhet och fått svar 4 eller 3\mathrm{,}7 eller 3\mathrm{,}71 (1 p.). | max 3 p. |
| Konstaterat 1h = 60 min. | + 0 p. |
| Om ekvationslösningen är felaktig men med god riktning, så ger andra raden | 1 p. |
| Timglaset är helt tömt då h=18. | (1 p.) |
| Värdet för parametern h insatt i uttrycket för tiden och beräknat tiden 120 min: 120\left(1-\left(1-\frac{18}{18}\right)^3\right)=120 | 2 p. |
| Bildat en korrekt proportionalitetsekvation \frac{13}{1}=\frac{120}{V} ELLER ekvation 13V=120 ELLER (\frac{120}{13} (2 p.) och förklaring (1 p.)). | 3 p. |
| Fått svaret V\approx 9{,}2 (dl) (svar och avrundning). (Om svaret ges i deciliter behövs ingen enhet.) | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Om värdet 120 min på tidsparametern inte alls förklarats, och h inte alls förekommer i uträkningarna, så ger de två första raderna i deluppgift 2 (0+1) poäng. | 1 p. |
| Om tiden beräknats med ett felaktigt värde på h, så ger de två första raderna i deluppgift 2 (0+1) poäng. | 1 p. |
| Om proportionalitetsekvationen är felaktig, ges inga poäng från de två sista raderna. | |
| Proportionalitetsekvationen i rad 3 är rätt om den har bildats med rätt logik, men möjligen med felaktiga värden hämtade från de två föregående raderna. Ekvationen är däremot felaktig om den exempelvis har formen \frac{13}{1}=\frac{V}{120}, eller om studenten exempelvis har antagit att tiden är direkt proportionell mot vätskans höjd. |
8. Vitaminhalt 12 p.
Ett företag tillverkar D3-vitaminkapslar. Enligt förpackningen innehåller en kapsel 50 mikrogram D3-vitamin. Företaget anlitar ett forskningsinstitut för att göra en kvalitetskontroll av kapslarna. Institutets mikrobiolog fastställer att mängden D3-vitamin i en kapsel är normalfördelad med väntevärdet 54,1 mikrogram och standardavvikelsen 8,4 mikrogram.
En vitaminkonsument tar på måfå en kapsel ur en förpackning. Med vilken sannolikhet innehåller kapseln minst 50 mikrogram D3-vitamin? (5 p.)
Företaget vill säkerställa att 95 % av kapslarna innehåller minst 50 mikrogram D3-vitamin. För vilket väntevärde på D3-vitaminmängden uppnås det här kravet i kvalitetskontrollen? Vi antar att ökningen av mängden vitamin inte påverkar standardavvikelsen. (7 p.)
| Använt kommando för normalfördelning. | 1 p. |
| Följande poäng kan man bara få om normalfördelningen använts. | |
| Satt in medelvärde 54{,}1 och standardavvikelse 8{,}4. | 1+1 p. |
| Valt rätt intervall X \ge 50. | 1 p. |
| Hämtat svaret exakt 68,7 %. | 1 p. |
| Löst genom test (en bild räcker). | |
| Testat ett värde i intervallet 63{,}5–64{,}0 och fått sannolikhet 0{,}95 med två gällande siffrors noggrannhet. | 2 p. |
| Hämtat svaret. | 1 p. |
| Tillräckligt noggrannt test: Fått värdet 63{,}82 eller noggrannare ELLER konstaterat att värdet 63{,}8 ger en sannolikhet under 0{,}95 och att värdet 63{,}9 ger en sannolikhet över 0{,}95 ELLER att intervallet med sannolikhet 0{,}95 för värdet 63{,}8 ger en gräns under 50, och för värdet 63{,}9 ger en gräns över 50 (endast 0 eller 2 poäng). | 2 p. |
| Svar exakt 63,8 ELLER med förklaring exakt 63,9. | 1 p. |
| Förklarat varför det inte finns andra lösningar. | 1 p. |
| Specifika anvisningar för denna lösning | |
| Intervall i fel riktning (X \leqslant 50): väntevärdet inom intervallet 36–36{,}5, exakt värde 36{,}18: (1+1+2+0+1) | max 5 p. |
| Samma felaktiga standardavvikelse i del 1 och 2: (2, om sannolikhetsvillkoret gäller +1+0+0+1) | max 4 p. |
| ELLER löst med direkt räkning | |
| Beräknat P(40{,}28323) = 0{,}95. | 1 p. |
| Beräknat avvikelsen från medelvärdet 50-40{,}28323 = 9{,}7168. | 3 p. |
| Flyttat medelvärdet till 54{,}1 + 9{,}7168 (\approx 63{,}8). | 2 p. |
| Svar exakt 63,8 ELLER med förklaring exakt 63,9. | 1 p. |
| ELLER löst med ekvation | |
| Ekvationen bildad med rätt idé. | 2 p. |
| Satt in värdena (8{,}4, 50, 0{,}95) korrekt. | 3 p. |
| Löst ekvationen. | 1 p. |
| Svar exakt 63,8 ELLER med förklaring exakt 63,9. | 1 p. |
| Specifika anvisningar för uppgiften | |
| Om normalfördelningstabell har används i lösningen, så räcker det att göra kontrollräkningar upp till tabellens noggrannhet. |
9. Förändringshastigheten för en funktion 12 p.
Vi undersöker polynomfunktionen p(x)=x^3+2x^2-11x-1.
Visa med en uträkning att den genomsnittliga förändringshastigheten för funktionen p i intervallet 0\le x\le 3 är 4. (4 p.)
Bestäm alla sådana punkter i intervallet 0\le x\le 3 där den momentana förändringshastigheten för funktionen p är lika stor som den genomsnittliga förändringshastigheten 4. (8 p.)
| Eftersom p(3)=11 och p(0)=-1, | 2 p. |
| är den genomsnittliga förändringshastigheten \frac{p(3)-p(0)}{3-0}=\frac{11-(-1)}{3-0}=4. | 2 p. |
| p'(x)=3x^2+4x-11 (en term rätt 1 p., bara en term fel 2 p.). | 3 p. |
| Den momentana förändringshastigheten är det samma som derivatan. | (1 p.) |
| STOP: Följande poäng endast om derivatan är ett andragradspolynom. | |
| Löst ekvationen p'(x)=4 med egen derivatafunktion ELLER löst ut när tangentens riktningskoefficient är 4. | 1 p. |
| (Exempelvis Solve-kommandot ger rötterna) x=-3 eller x=\frac{5}{3} (närmevärde godkänns). | 2 p. |
| Av dessa är x= exakt \frac{5}{3} i det givna intervallet. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Derivatan kan ha beräknats i deluppgift 1. | |
| Med programvara testat när tangentens riktningskoefficient är fyra, och fått: (x\approx 1{,}67 och testat i intervallet [0,3]) ELLER (x=-3 och x\approx 1{,}67) (0+1+1+2+0) | max 4 p. |
| Inga poäng från den näst sista raden om man löst någon annan ekvation än p'(x)=4 (bortsett från uppenbara tryckfel). | |
| Startpoäng: Förstått att derivatan är användbar i denna uppgift. | 1 p. |
Del B2
10. En elevs lösningsmetod 12 p.
En elev berättar att hen har kommit på ett enkelt sätt att utföra en division av bråk: "Jag dividerar täljarna med varandra och nämnarna med varandra, vilket gör att jag får svaret direkt i bråkform." Som exempel nämner hen
\frac3{20}:\frac14 = \frac{3:1}{20:4}=\frac35.
Är slutresultatet av exempeluträkningen korrekt? (2 p.)
Beräkna \frac6{35} : \frac35 med elevens metod. (4 p.)
Ta fram ett exempel där beräkningsmetoden som slutresultat ger ett bråk som inte är i förenklad form. (6 p.)
Här är ett bråk en beteckning i formen \frac nm eller -\frac nm, där n är ett naturligt tal och m ett positivt heltal.
| \frac{3}{20} : \frac{1}{4} = \frac{3}{20} \cdot \frac{4}{1} ELLER \frac{3}{20} : \frac{1}{4} = \frac{12}{20} ELLER med räknare \frac{3}{20} : \frac{1}{4} = 0{,}6 \left(= \frac{3}{5}\right) | 1 p. |
| = \frac{12}{20}, så resultatet är rätt ELLER = \frac{3}{5} (, så resultatet är rätt). | 1 p. |
| \left(\frac{6}{35} : \frac{3}{5} =\right) \frac{6:3}{35:5}, täljare 1 p. + nämnare 1 p. (med egna bråktal) | 2 p. |
| exakt = \frac{2}{7} | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Inte använt den angivna lösningsmetoden (eller lösningsmetoden framgår inte). | 0 p. |
| Kopieringsfel (2+0). | max 2 p. |
| Med division av bråk menas beteckningen \pm \frac{n_1}{m_1} : \pm\frac{n_2}{m_2} (eller motsvarande), där n_1 är ett naturligt tal och n_2, m_1 och m_2 är positiva heltal. En division av bråk är fungerande (med avseende på denna uppgift), om n_1/n_2=a är ett heltal, m_1/m_2=b är ett heltal, och heltalen a och b har gemensamma delare. |
| Givit en division av bråk, enligt uppgiftens definition, som inte är samma som i uppgiftstexten. | 1 p. |
| oberoende Påpekat eller visat att resultatet av uträkningen inte är i förenklad form, eller förenklat bråket. (Denna poäng gäller slutresultatet av uträkningarna, även om de framkommit efter felaktiga uträkningar, så länge de ursprungliga talens täljare och nämnare är heltal.) | 1 p. |
| STOP: Följande poäng kan bara fås om det givna exemplet är en fungerande division av bråk. | |
| Det givna exemplet är en fungerande division av bråk. | 1 p. |
| Som slutsats: = \pm \frac{n_1: n_2}{m_1 : m_2} | (1+1 p.) |
| Som slutsats: = \pm \frac{a}{b} (genomfört divisionerna) | 1 p. |
| Specifika anvisningar för deluppgiften | |
| En täljare eller nämnare i de givna exempeltalen är ett negativt heltal (0+1+1+2+1). | max 5 p. |
| Divisionen inte genomförd med lösningsmetoden i uppgiften, men det givna paret är fungerande. (1+1+1+0+0). | max 3 p. |
| Exempel: Inte förenklad form: \frac{8}{4}, \frac{0}{2}. Förenklad form: \frac{3}{4}, \frac{3}{1}, \frac{1}{1} och \frac{0}{1}. |
11. En mjölkförpackning 12 p.
Vi gör en modell av en mjölkförpackning som utgörs av ett rätblock och en övre del ovanpå det. Vi antar att mjölken i en full mjölkförpackning exakt fyller rätblocksdelen av mjölkförpackningen.
För både en mjölkförpackning på 1 liter och en på 1,75 liter gäller det att bottnen är en kvadrat och att rätblocksdelens höjd är 20 cm. Bestäm längden på bottenkvadratens sida i båda fallen. (4 p.)
Vi uppskattar mängden material för förpackningen med formeln A_1+4{,}5\cdot A_2, där A_1 är den sammanlagda arean av rätblockets sidoytor och A_2 bottenkvadratens area. I vilken mjölkförpackning finns det mera förpackningsmaterial i förhållande till mängden mjölk? (8 p.)
| Bottenarean av den större mjölkförpackningen är \frac{1\mathrm{,}75 \text{ dm}^3}{2\text{ dm}} =0\mathrm{,}875\, \textrm{dm}^2, | 1 p. |
| så sidlängden av dess bottenyta är \sqrt{0\mathrm{,}875\text{ dm}^2}=0{,}935414\ldots \text{ dm} \approx 0\mathrm{,}94\, \textrm{dm}=9{,}4\, \textrm{cm}. | 1 p. |
| Bottenarean av den mindre mjölkförpackningen är \frac{1 \text{ dm}^3}{2\text{ dm}} =0\mathrm{,}5\, \textrm{dm}^2, | 1 p. |
| så sidlängden av dess bottenyta är \sqrt{0\mathrm{,}5 \text{ dm}^2}=0{,}707107\ldots \text{ dm}\approx 0\mathrm{,}71 \text{ dm}= 7{,}1\, \textrm{cm}. | 1 p. |
| ELLER | |
| Bildat rätt ekvationer, med enheter iakttagna på något sätt (till exempel 1000 = x^2 \cdot 20, 1=x^2\cdot2 eller 1 \textrm{l}= x^2 \cdot 20 \textrm{ cm} och så vidare.) | 2 p. |
| Rätt sidlängder lösta från ekvationen (för hand eller med programvara). | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Svaret får ges med 1, 2 eller 3 gällande siffrors noggrannhet. | |
| Fel enhetsomvandling ELLER ingen hänsyn tagen till enheter: -1 p./förpackning | |
| Startpoäng: Kompatibel enhetsomvandling, till exempel höjd 2 dm och volym 1 dm^3 eller höjd 20 cm och volym 1000 cm^3. | 1 p. |
| Gissat svar med minst två gällande siffrors noggrannhet och kontrollerat: 1 p./förpackning | max 2 p. |
| Beräknat arean av en sidoyta av någon av förpackningarna | (1 p.) |
| Totala arean av den större förpackningens sidoytor 4\cdot 2\cdot 0\mathrm{,}935\ldots \, \textrm{dm}^2=7{,}483... \text{ dm}^2. | 1 p. |
| Materialåtgången för den större förpackningen är alltså (4\mathrm{,}5\cdot 0\mathrm{,}875+4\cdot 2\cdot 0\mathrm{,}935 \ldots )\, \textrm{dm}^2=11{,}420\ldots \text{ dm}^2. | 1 p. |
| Förhållandet är \frac{(4\mathrm{,}5\cdot0\mathrm{,}875+4\cdot 2\cdot 0\mathrm{,}935\ldots )\, \textrm{dm}^2}{1\mathrm{,}75\mathrm{l}}\approx 6\mathrm{,}526\ldots \, \frac{\textrm{dm}^2}{\mathrm{l}}. | 1 p. |
| På samma sätt är den totala arean av den mindre förpackningens sidoytor 4\cdot 2\cdot 0\mathrm{,}707\ldots \, \textrm{dm}^2=5{,}656... \text{ dm}^2. | 1 p. |
| Materialåtgången för den mindre förpackningen är alltså (4\mathrm{,}5\cdot0\mathrm{,}5+4\cdot 2\cdot 0\mathrm{,}707\ldots )\, \textrm{dm}^2=7{,}906\ldots \text{ dm}^2. | 1 p. |
| Förhållandet är \frac{(4\mathrm{,}5\cdot0\mathrm{,}5+4\cdot 2\cdot 0\mathrm{,}707 \ldots )\, \textrm{dm}^2}{1\mathrm{l}}\approx 7\mathrm{,}906\ldots \, \frac{\textrm{dm}^2}{\mathrm{l}}. | 1 p. |
| Som slutsats av rad 4 och 7: Den mindre förpackningen använder mer material i förhållande till mängden mjölk. | 1 p. |
| Specifika anvisningar för deluppgiften | |
| Fortplantat fel från deluppgift 1. | max 8 p. |
| Poängen från rad 4 och 7 kan fås genom att beräkna vilket förhållande som helst, från vilken slutsatsen kan dras. | |
| Om sidoytans area inte multiplicerats med fyra, dras av 1 p./förpackning (rad 2 och 5), men de nedre raderna kan fortfarande ge poäng. | |
| Ett systematiskt mindre fel, som upprepas för båda förpackningarna: poängavdrag bara för den ena förpackningen. | |
| Mellanstegen bör ha minst två gällande siffror. Annars -1 p. för hela deluppgiften. |
12. Sannolikhetslärans ursprung 12 p.
Sannolikhetsläran har sitt ursprung i 1600-talets Frankrike, där man i vissa kretsar sysslade med hasardspel. Antoine Gombaud var en fransk författare och hasardspelare som märkte att sannolikheten att vinna var olika i två tärningsspel, men han kunde inte motivera detta matematiskt. Eftersom Gombaud också använde namnet Chevalier de Méré kallas detta de Mérés problem. Spelens principer är följande:
I båda spelen spelade en utmanare mot de Méré. Utmanaren och de Méré lade lika mycket pengar i potten och vinnaren fick hela potten.
I det första spelet kastade de Méré en tärning fyra gånger. Om han fick minst en sexa vann hann, annars förlorade han. Erfarenheten visade att det här var ett lönsamt spel för de Méré.
I det andra spelet kastade de Méré två tärningar samtidigt 24 gånger. Om han fick minst en dubbelsexa vann han, annars förlorade han. Det här spelet visade sig emellertid vara förlustbringande för de Méré.
För att besvara de Mérés problem utvecklade två samtida matematiker, Blaise Pascal och Pierre de Fermat, grunderna för sannolikhetsteori och visade att de Méré på lång sikt vinner i det första spelet och förlorar i det andra. Visa detta med sannolikhetslärans metoder.
| Spel 1 | |
| Sannolikheten för att inte få någon sexa på fyra kast är \left(\frac{5}{6}\right)^4 (uttryck på formen x^y, där x är en sannolikhet och y >1, y\in \mathbb{N}; \frac{5}{6}; exponent 4), | 1+1+1 p. |
| så de Mérés vinstsannolikhet i det första spelet är enligt komplementsannolikheten 1-\left(\frac{5}{6}\right)^4=\frac{671}{1296}\approx 0\mathrm{,}52. (Idé om komplementhändelsen (1 p.). Andra poängen ges endast om första raden gett minst 2 p.) | 2 p. |
| Vi har ganska exakt 0\mathrm{,}52>0\mathrm{,}5 ELLER slutsats i text. | 1 p. |
| ELLER med binomialkoefficienter | |
| Beräknat sannolikheterna P(1\ \text{sexa}), P(2\ \text{sexor}),\ P(3\ \text{sexor}),\ P(4\ \text{sexor}) exempelvis via kombinationer: \binom{4}{1} \left( \frac{1}{6} \right)\left(\frac{5}{6}\right)^3,\ \binom{4}{2} \left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^2,\ \binom{4}{3} \left(\frac{1}{6}\right)^3\left(\frac{5}{6}\right),\ \binom{4}{4} \left(\frac{1}{6}\right)^4\left(\frac{5}{6}\right)^0. | |
| (igenkännlig formel för binomialsannolikheter 1 p., en term rätt 2 p., tre termer rätt 3 p., fyra termer rätt och inga överflödiga termer 4 p.) | 4 p. |
| Beräknat en summa av 2–4 sannolikheter, varav minst två är korrekta. Resultatet är i intervallet (0, 1). (\frac{671}{1296}\approx 0\mathrm{,}52) | 1 p. |
| Vi har ganska exakt 0\mathrm{,}52>0\mathrm{,}5 ELLER slutsats i text. | 1 p. |
| ELLER med programvara för binomialfördelning | |
| Använt kommando eller programvara för binomialfördelning. | 1 p. |
| Som slutsats: Satt in parametrarna n= 4 och p=\frac16 (närmevärde godkänns) i programvaran. | 1+1 p. |
| Valt rätt intervall (1\le X) eller nedre gräns. | 1 p. |
| Fått sannolikheten 0{,}52. | 1 p. |
| Vi har ganska exakt 0\mathrm{,}52>0\mathrm{,}5 ELLER slutsats i text. | 1 p. |
| Spel 2 | |
| Sannolikheten för att inte få något par av sexor på 24 kast är \left(\frac{35}{36}\right)^{24}, för det finns 36 par av utfall. (täljare 35, nämnare 36, exponent 24) | 1+1+1 p. |
| så de Mérés vinstsannolikhet i det första spelet är enligt komplementsannolikheten 1-\left(\frac{35}{36}\right)^{24}\approx 0\mathrm{,}49. (Idé om komplementhändelsen (1 p.). Andra poängen ges endast om första raden gett minst 2 p.) | 2 p. |
| Vi har ganska exakt 0\mathrm{,}49<0\mathrm{,}5 ELLER slutsats i text. | 1 p. |
| ELLER med programvara för binomialfördelning | |
| Använt kommando eller programvara för binomialfördelning. | 1 p. |
| Som slutsats: Satt in parametrarna n= 24 och p=\frac1{36} (närmevärde godkänns) i programvaran. | 1+1 p. |
| Valt rätt intervall (1\le X) och fått sannolikheten 0{,} 49. | 2 p. |
| Vi har ganska exakt 0\mathrm{,}49<0\mathrm{,}5 ELLER slutsats i text. | 1 p. |
| Specifika anvisningar för uppgiften | |
| Alla noggrannheter, som räcker för att göra jämförelsen, godkänns. | |
| Bristande förklaringar -1 p./spel, med början från den andra poängen av vardera spelet. Programvarulösningar och liknande kräver också förklaring. Här bör förklaringen koppla samman skärmdumpen med situationen i uppgiften. | |
| Parenterser saknas i bråkpotensen, men uträkningarna korrekta: Standardavdrag för dålig notation -1 p. för hela uppgiften. |
13. En deriverande rymdsond 12 p.
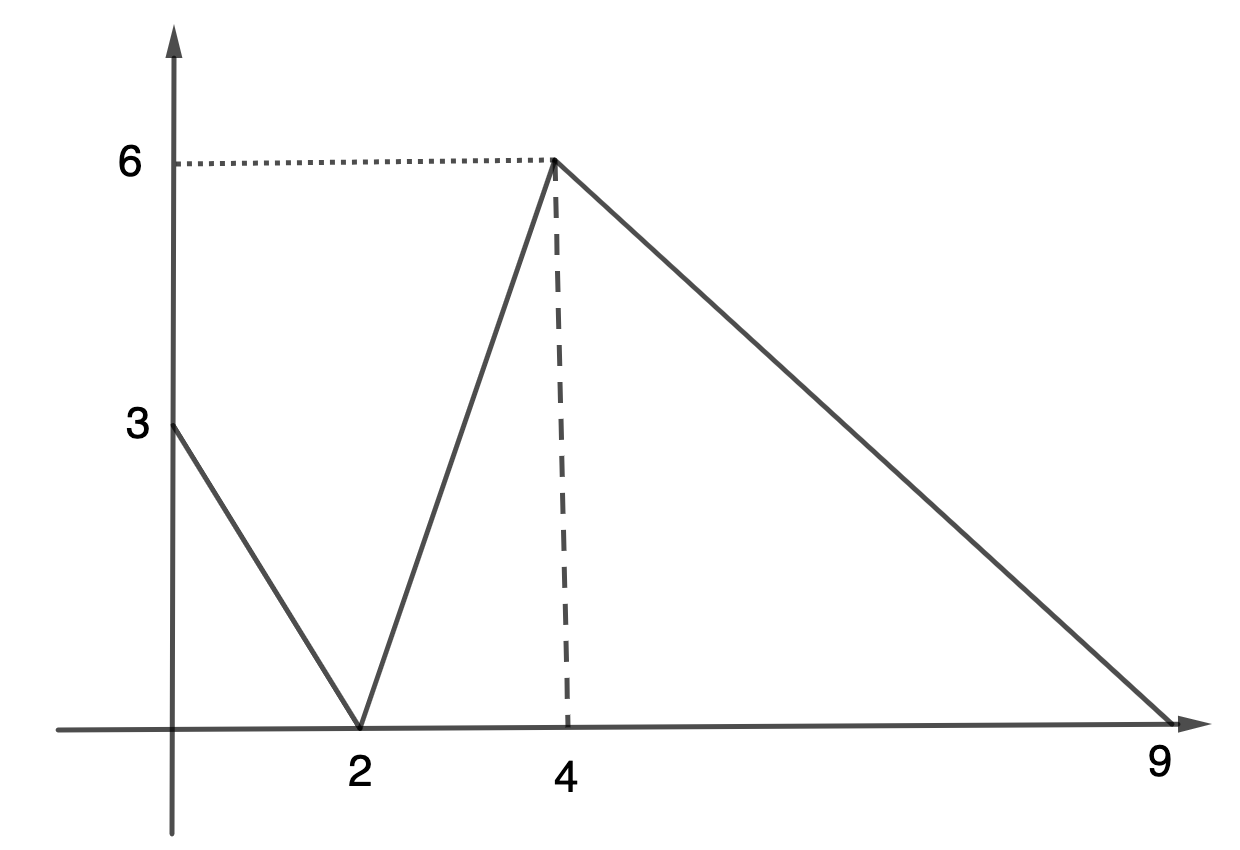
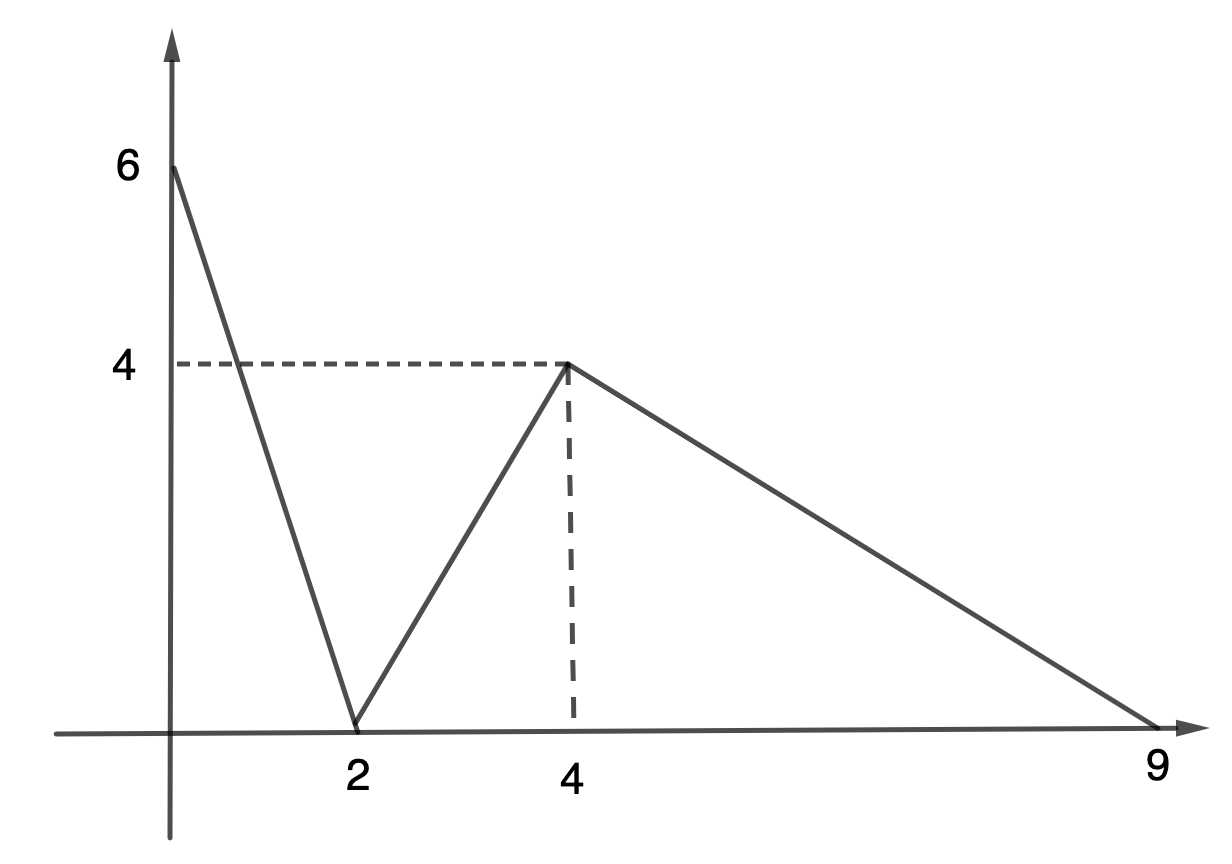
En rymdsond mäter temperaturen på en planet. Den skulle skicka data om temperaturen som en funktion T(t) i tidsintervallet 0\le t\le 9. På grund av ett programvarufel fick man bara uppgiften att funktionens derivata T'(t) är negativ då t<2, positiv då 2<t<4, och åter negativ då t>4. Forskarna funderade på vad man utifrån detta kan säga om temperaturen T.
Utforma ett exempel på grafen av temperaturfunktionen T, som dessutom har den egenskapen att temperaturens största värde uppnås vid tidpunkten t=4. (6 p.)
Utforma ett exempel på grafen av temperaturfunktionen T, som dessutom har den egenskapen att temperaturens största värde inte uppnås vid tidpunkten t=4. (6 p.)
Förklara i vardera fallet i ord hur de efterfrågade egenskaperna hos temperaturfunktionen syns i grafen.
| Bild | |
| Grafen kontinuerlig och ''ser deriverbar ut'' upp till den noggrannhet som bilden tillåter, möjligen bortsett från vid tidpunkterna t=0, 2, 4, 9. | |
| STOP: Följande poäng kan endast fås om villkoren ovan är uppfyllda. | |
| Monoton på rätt sätt i rätt intervall. | 1 p. |
| Om föregående är uppfyllt: det största värdet uppnås då t=4. | 3 p. |
| Förklaring i text: sambandet mellan derivata och avtagande / växande + noterat att det största värdet uppnås då t=4. | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Grafen definierad på ett felaktigt intervall, som dock innehåller åtminstone [1,5] | –1 p. |
| Om grafen ritad på ett större intervall så ges -1 p., enligt föregående punkt, och bedömningen tar bara hänsyn till intervallet [0,9]. | |
| Förklaringar i text ger bara poäng om det som förklaras också syns i bilden. Notera att exempelvis en parabel med topp i punkten t=4 ger möjlighet till en förklaringspoäng, men ingen bildpoäng. | |
| Ett teckenschema ger inte ensamt poäng, men kan i kombination med en bild ge förklaringspoäng. | |
| Exempel på graf: |
| Bild | |
| Grafen kontinuerlig och ''ser deriverbar ut'' upp till den noggrannhet som bilden tillåter, möjligen bortsett från vid tidpunkterna t=0, 2, 4, 9. | |
| STOP: Följande poäng kan endast fås om villkoren ovan är uppfyllda. | |
| Monoton på rätt sätt i rätt intervall. | 1 p. |
| Om föregående är uppfyllt: det största värdet uppnås inte då t=4. | 3 p. |
| Förklaring i text: sambandet mellan derivata och avtagande / växande (kan hänvisa till föregående deluppgift) + noterat att det största värdet inte är i t=4. | 2 p. |
| Specifika anvisningar för deluppgiften | |
| Grafen definierad på fel intervall, men som innehåller åtminstone [1,5] | –1 p. |
| Om grafen ritad på ett större intervall så ges -1 p, enligt föregående punkt, och bedömningen tar bara hänsyn till intervallet [0,9]. | |
| Förklaringar i text ger bara poäng om det som förklaras också syns i bilden. | |
| Ett teckenschema ger inte ensamt poäng, men kan i kombination med en bild ge förklaringspoäng. | |
| Exempel på graf: |