Hyvän vastauksen piirteet: FI – Fysiikka
27.3.2024
Lopulliset hyvän vastauksen piirteet 14.5.2024
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
15.5.2024 klo 15.30 korjattu lukuarvo osatehtävässä 2.3, täsmennetty sanamuotoja osatehtävissä 5.2 ja 5.3 sekä lisätty yksi esimerkki tyypillisistä virheistä tehtävään 4.
Osa 1: 20 pisteen tehtävä
1. Monivalintatehtäviä fysiikan eri osa-alueilta 20 p.
Valitse jokaisessa osatehtävässä parhaiten soveltuva vaihtoehto. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 Kahdeksasluokkalainen mittaa 60 metrin juoksuun kuluvan ajan älypuhelimen ajanottotoiminnolla. Millä tarkkuudella tulos on mielekästä ilmoittaa? 2 p.
- 0,1 s (2 p.)
1.2 Missä seuraavista mittaustuloksista on suurin suhteellinen virhe? 2 p.
- 2,2 kg ± 0,2 kg (2 p.)
1.3 Mikä on kodin sähkösaunan energiankulutuksen suuruusluokka yhdellä saunomiskerralla? 2 p.
- 8 kWh (2 p.)
1.4 Mikä seuraavista matkustusmuodoista kuluttaa eniten energiaa yhtä henkilöä ja yhtä kilometriä kohti? 2 p.
- Lentokone (2 p.)
1.5 Miten ilmakehän kasvihuonekaasut lämmittävät maapalloa? 2 p.
- Ne absorboivat maapallon pinnan säteilyä, joten ilmakehä lämpenee ja maapallon lämpötila nousee. (2 p.)
1.6 Millä voimalaitostyypillä Suomessa tuotetun sähköenergian määrä on kasvanut eniten 2020-luvulla? 2 p.
- Tuulivoimalaitokset (2 p.)
1.7 Mikä perusvuorovaikutuksista on voimakkain hyvin pienillä etäisyyksillä (< 1 fm)? 2 p.
- Vahva vuorovaikutus (2 p.)
1.8 Kuinka suuri osa maailmankaikkeuden koostumuksesta on tuntemaamme tavallista ainetta? 2 p.
- 5 % (2 p.)
1.9 Kuulakärkikynän kierrejousta puristetaan kokoon 2,5 N:n voimalla, jolloin se lyhenee 0,1 cm. Voidaanko tämän perusteella päätellä, että 2 500 N:n voimalla venytettäessä kyseisen jousen pituus kasvaa 100 cm? 2 p.
- Ei, koska jousta ei voi venyttää niin pitkäksi. (2 p.)
1.10 Havaitusta uudesta fysikaalisesta ilmiöstä luotiin malli, jonka pätevyyttä testattiin kokeellisesti. Mallin mukainen ennuste ja kokeellinen tulos olivat ristiriidassa. Miten tutkimuksen tulee edetä tästä? 2 p.
- Jos kokeen suorituksesta ei löydy ilmeistä virhettä, luotua mallia on muutettava. (2 p.)
Osa 2: 15 pisteen tehtävät
2. Omenamehupuristin 15 p.
Omenamehupuristimella (kuva ) tehdään omenoista tuoremehua. Omenat murskataan ja pannaan suodatinpussiin ja edelleen kuvassa näkyvään metalliastiaan. Metalliastian seinät ovat täynnä reikiä, jotta mehu pääsee valumaan ulos. Puristimen kampea pyörittämällä mäntä painuu alaspäin ja puristaa omenamurskaa.
Puristimen kampea kierrettiin yksi kierros kerrallaan ja ulos valuneen mehun tilavuus mitattiin. Mittaustulokset on esitetty aineistossa .
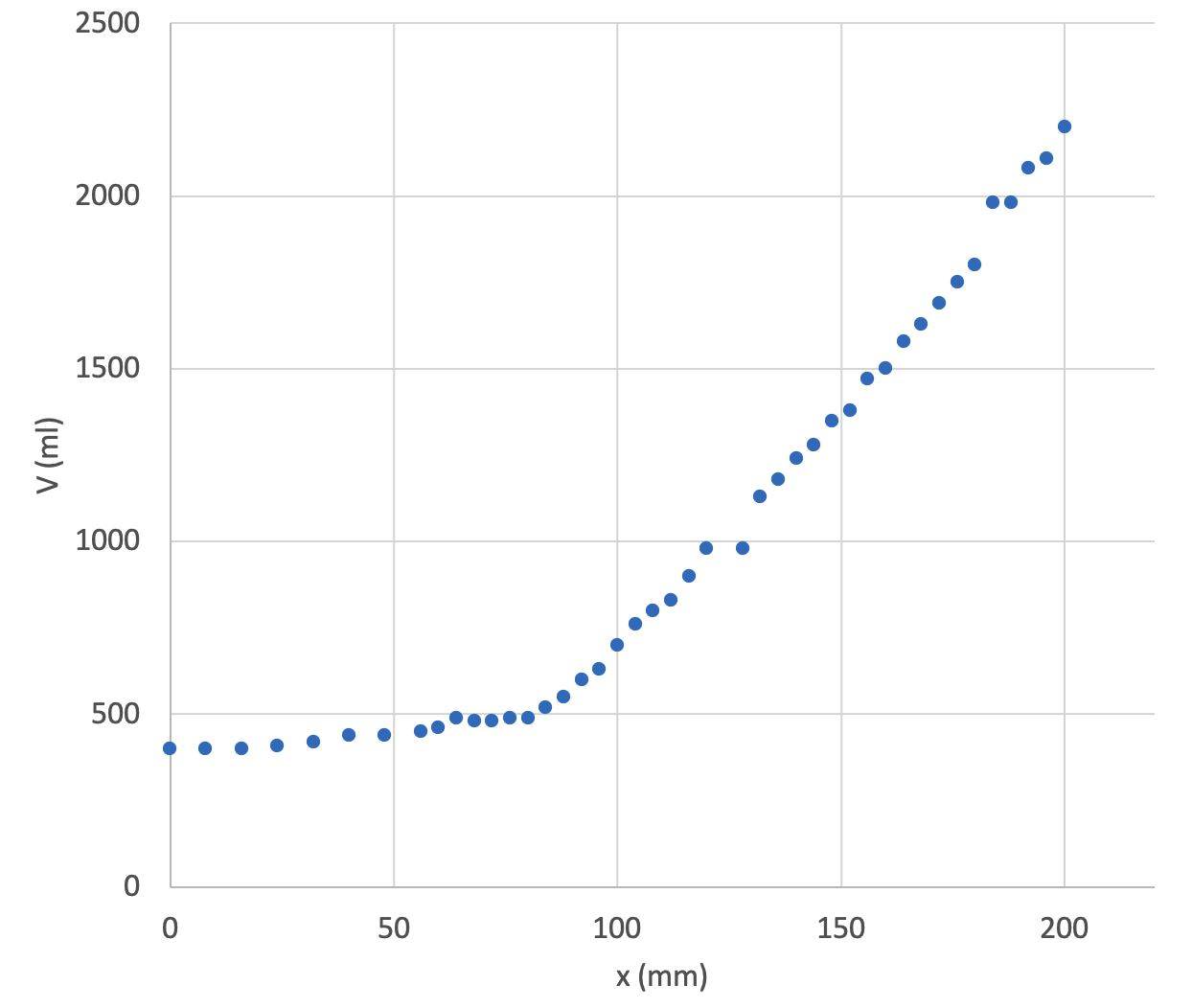
2.1 Esitä graafisesti mehun tilavuus männän ylimmästä asemastaan liikkuman matkan funktiona. Yksi kammen kierros vastaa 4,0 mm:n pystysuoraa liikettä. Esityksessä tulee näkyä mittaustuloksia vastaavat pisteet, mutta ei pisteitä yhdistäviä viivoja. 5 p.
Taulukkolaskennan avulla luodaan uusi taulukko, jossa sarakkeina on männän yläasennosta kulkema matka ja mehun tilavuus. Piirretään kuvaaja.
Pisteytys:
Tyypillinen virhe:
On esitetty kuvaaja, jossa mitatut tilavuuden arvot männän liikkuman matkan funktiona näkyvät erillisinä mittauspisteinä. (5 p.).
Jos tilavuus on piirretty kierrosten funktiona, vähennetään kolme pistettä.
Jos mittauspisteet eivät näy tai niitä puuttuu, vähennetään kaksi pistettä.
Jos pisteet on yhdistetty murtoviivalla, vähennetään yksi piste.
Jos akselin lukuarvot ovat väärin tai puuttuvat tai akselit ovat väärin päin, vähennetään kaksi pistettä.
Jos suureen tunnus puuttuu tai yksikkö puuttuu, vähennetään kustakin virheestä yksi piste.
On piirretty kuvaajaan sovite. Tämän virheen takia ei vähennetty kuvaajasta annettavia pisteitä.
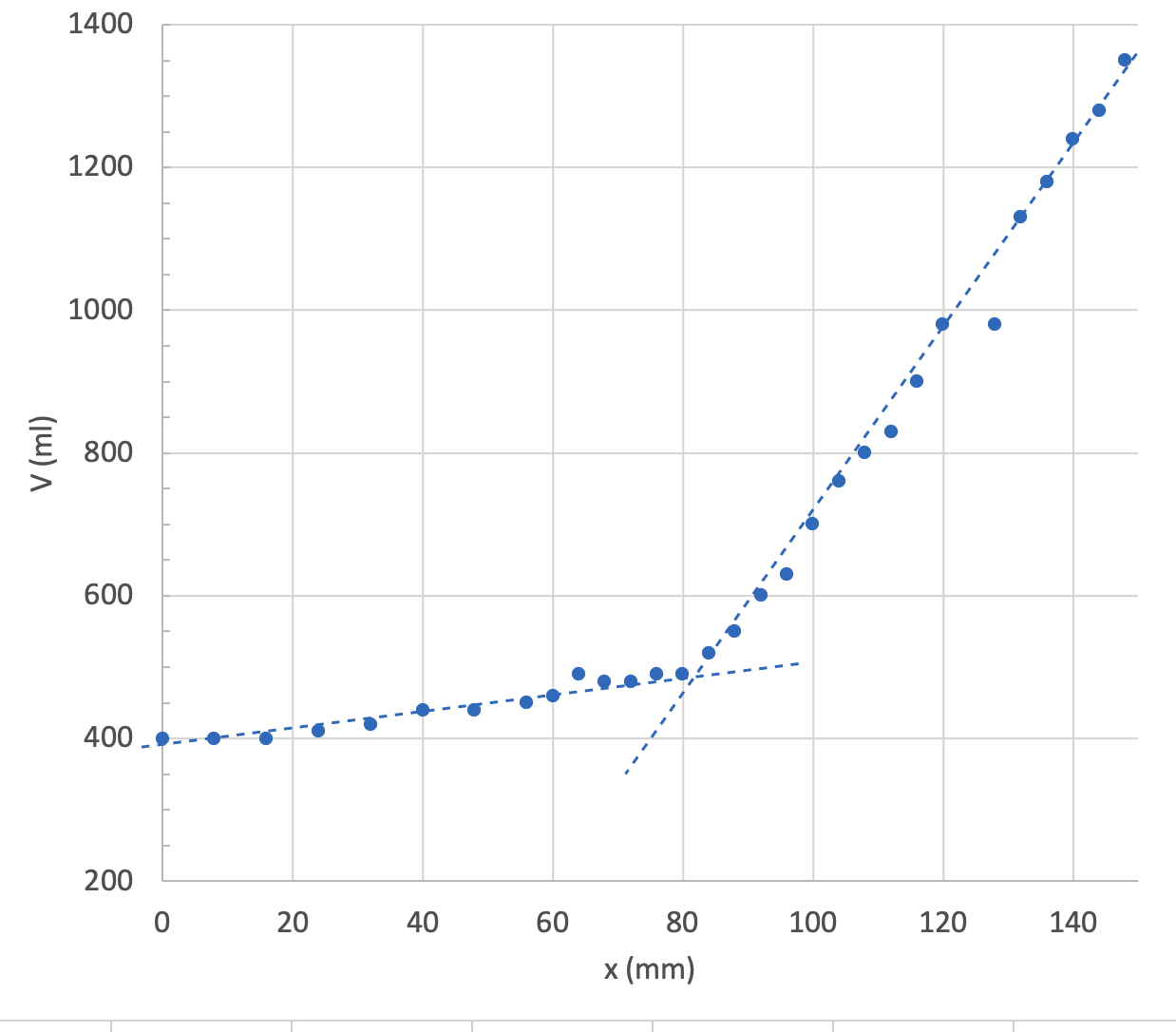
2.2 Kuten kuvasta näkyy, kampea pitää kiertää useita kierroksia ennen kuin mäntä saavuttaa omenamurskeen. Määritä osatehtävässä 2.1 piirtämääsi kuvaajaa pohjana käyttäen, kuinka paljon mehua omenoista saatiin ennen kuin mäntä saavutti murskeen. 4 p.
Graafisessa esityksessä näkyy kaksi osaa, joita kumpaakin voi approksimoida suoralla. Suorien leikkauspiste asettuu noin 500 ml:n kohdalle.
Mehua saadaan puristamatta noin 0,5 litraa.
Pisteytys:
Annettu vastauksena 1–2 merkitsevän numeron tarkkuudella mehun tilavuus välillä 490 ml – 500 ml (2 p.). Muusta tarkkuudesta vähennetään yksi piste.
Jos vastauksessa on kerrottu oletus, että mehua oli astiassa aluksi 400 ml ja sitä käyttäen annettu vastaukseksi 90 ml -100 ml, vastaus luetaan oikeaksi.
Mehun määrä on perusteltu viittaamalla graafisen esityksen kohtaan x= 80 mm (2 p.).
Tyypillinen virhe:
On annettu vastaus ilman kuvaajaa tai jätetty viittaamatta osatehtävässä 2.1 piirrettyyn kuvaajaan.
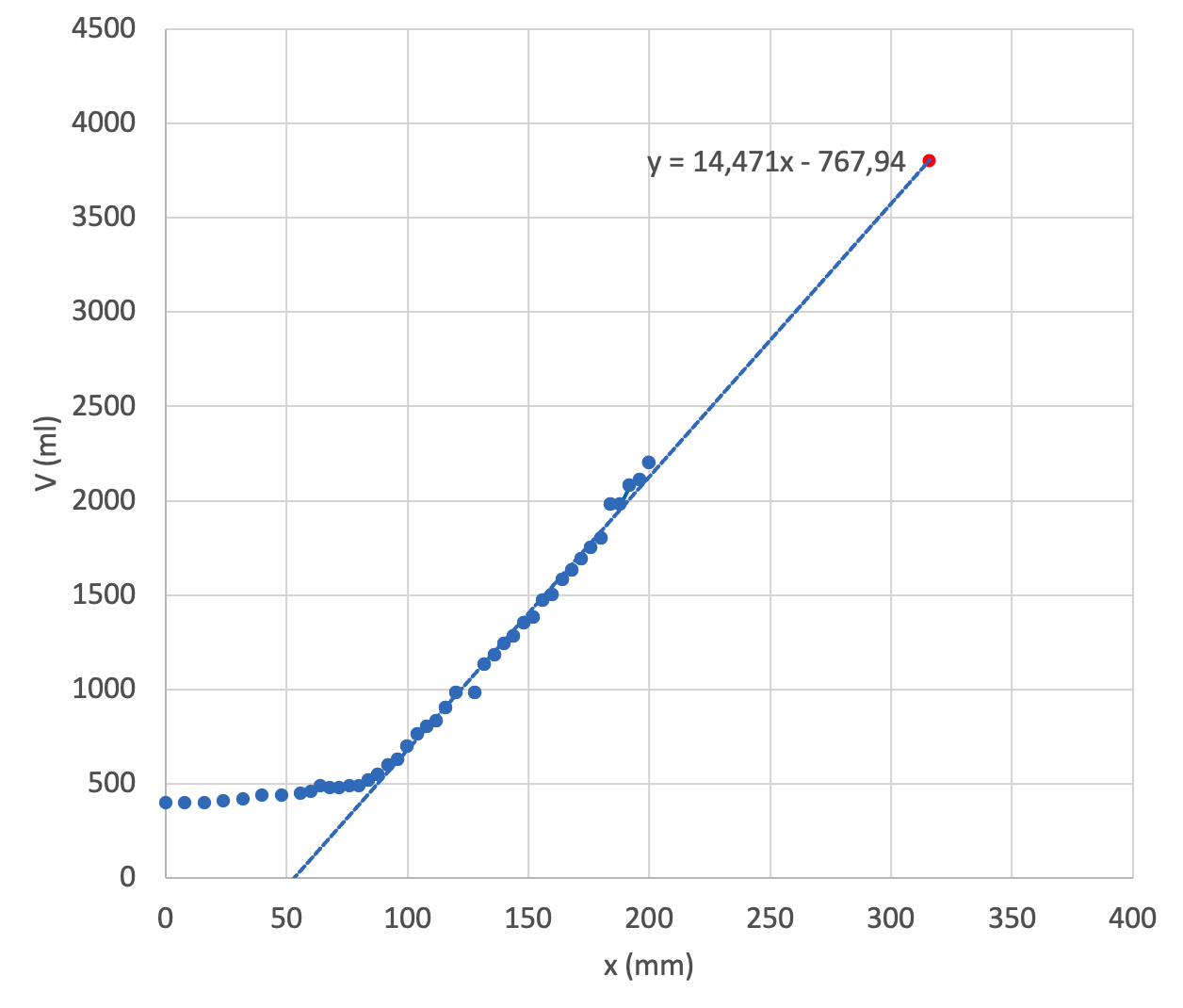
2.3 Omenoiden puristusta jatkettiin siihen asti, että kampea oli kierretty yhteensä 79 kierrosta. Mehua saatiin samassa suhteessa tilavuuden pienenemiseen verrattuna. Arvioi graafista esitystä käyttäen, kuinka paljon mehua omenoista kokonaisuudessaan saatiin. 6 p.
Sovitetaan mittauspisteistön loppuosaan suora, josta luetaan 316 mm:n kohdalta saadun mehun määräksi 3,8 litraa.
Vaihtoehtoisesti graafisesta esityksestä saadaan suoran yhtälöksi V(x) = 14,5 l/m · x – 0,768 l. Tästä saadaan arvolla x = 316 mm 3,8 litraa.
Pisteytys:
Ratkaisussa on kerrottu tai siihen piirretystä kuvaajasta näkyy, että ekstrapoloidaan arvoon 316 mm tai 79 kierrosta. (2 p.)
Ratkaisussa on annettu oikea vastaus 2–3 merkitsevän numeron tarkkuudella välillä 3,8 L – 4,1 L ja näytetty joko ekstrapolaatio kuvaajassa tai käytetty suoran yhtälöä lopputuloksen laskemiseen (4 p.). Muusta tarkkuudesta vähennetään yksi piste.
Tyypillinen virhe:
On piirretty kuvaajaan jokin muu sovite kuin suora, jolloin lopputulos on selvästi väärin.
3. Uudenvuodentinojen valaminen 15 p.
3.1 Osoita, että kidesokerin sulattamiseen tarvitaan 8,2 kJ energiaa, jos huoneenlämpöistä (21°C) sokeria otetaan kaksi ruokalusikallista (30 ml). 7 p.
Sokerin sulattamiseen tarvittava energiamäärä kuluu sen lämmittämiseen ja sulattamiseen: Q = cm\Delta T + sm , missä c on sokerin ominaislämpökapasiteetti ja s sokerin ominaissulamislämpö.
Aineistossa on annettu molaarinen lämpökapasiteetti c’ ja molaarinen sulamislämpö s’. Näiden avulla yhtälö tulee kirjoittaa
Q = c’ n \Delta T + s’ n.Sokerin massa on m=\rho V =30\,{\rm ml}\cdot (80\,{\rm g})/(100\,{\rm ml})=24\,{\rm g}.
Sokerin ainemäärä on n = \frac{m}{M} = \frac{24\,{\rm g}}{342,3\,{\rm g/mol} } = 0,070 {\rm mol}.
Sokerin lämpötilan muutos huoneenlämpötilasta sulamispisteeseen on \Delta T=462\,{\rm K} - (273,15+21)\, {\rm K}=167,85\,{\rm K}.
Tarvittava energia on Q = 0,4225\,{\rm kJ/(mol \cdot K)} \cdot 0,070 {\rm mol} \cdot 167,85\,{\rm K} + 46,2\,{\rm kJ/mol} \cdot 0,070 {\rm mol} = 8,198 {\rm kJ}.
Pisteytys:
On esitetty lämmittämisen tarvitseman energian suureyhtälö (2 p.) ja sulamisen tarvitseman energian suureyhtälö (2 p.).
On laskettu oikea vastaus ja todettu sen olevan 2–3 merkitsevän numeron tarkkuudella 8,2 kJ (3 p.). Muusta tarkkuudesta vähennetään yksi piste.
Jos ratkaisussa on tulkittu sokerin tilavuudeksi 60 ml, laskettu sen avulla tarvittavaksi energiaksi 16,4 kJ ja kommentoitu saatua tulosta järkevästi, ratkaisu luetaan oikeaksi.
3.2 Osatehtävän 3.1 sokerimäärä sulatetaan levyllä, jonka teho on 1 200 W. Sulaminen kestää 2,5 minuuttia. Määritä sulattamisen hyötysuhde. 4 p.
Kohdan 3.1 perusteella sokerin sulattaminen vaatii Q=8\,212\,{\rm J} energiaa. Sähkölieden levyn teho on P=1\,200\,{\rm W}, joten lieden tuottama energia on E=Pt. Hyötysuhde on
\eta=\frac{Q}{Pt}=\frac{8212\,{\rm J}}{1200\,{\rm W}\cdot 2,5\cdot 60\,{\rm s}}=0,046.
Hyötysuhde on siis 4,6 %.
Pisteytys:
On esitetty hyötysuhteelle ratkaistu oikea suureyhtälö (2 p).
On annettu oikea vastaus 2–3 merkitsevän numeron tarkkuudella välillä 4,4 % – 4,7 % (2 p). Muusta tarkkuudesta vähennetään yksi piste.
3.3 Video esittää rinnakkain lyijyn ja sokerin kuumentamista liedellä samoissa olosuhteissa. Lyijykimpale sulaa kokonaan lyhyen ajan kuluessa, mutta sokerikekoa sulatettaessa osa sokerista ei sula pitkään aikaan. Mistä ero johtuu? 4 p.
Videoiden alkuhetkellä kummankin aineen sulaminen alkaa. Tästä voidaan päätellä, että pannua koskettava materiaali on saavuttanut sulamispisteensä. Lyijykappale sulaa nopeasti, sillä hyvän lämmönjohtavuuden takia kappaleessa ei ole merkittäviä lämpötilaeroja. Sokerikeko sulaa ensin reunalta, ja sulaminen edistyy hitaasti. Tämän aiheuttaa lämmön heikko siirtyminen pannua koskettavasta sokerista kauemmas. Sulamispisteitä vertaamalla havaitaan, että lyijyä sulattavassa pannussa on korkeampi lämpötila kuin sokeripannussa. Pannusta ympäristöön siirtyvän hukkalämmön teho on suurempi lyijypannulla, joten aikayksikössä sokeriin siirtyy suurempi lämpömäärä.
Ero johtuu siis eroista aineiden lämmönjohtavuudessa. Metalli johtaa lämpöä paremmin kuin sokeri. Lisäksi lämpö johtuu kappaleesta toiseen, eli sokerikiteestä toiseen, huomattavasti heikommin kuin yhtenäisen metallikappaleen sisällä.
Pisteytys:
On kerrottu, että lyijyn lämmönjohtavuus on suurempi kuin sokerin (2 p.).
On kerrottu, että lämmönsiirto yhtenäisessä metallikappaleessa tapahtuu tehokkaammin kuin rakeisessa aineessa (2 p.).
Tyypillinen virhe:
On perusteltu eroa aineiden sulamispisteillä, ominaislämpökapasiteeteilla tai lämpökapasiteeteilla.
4. Voimat 15 p.
4.1 Ilmassa lentävä nuoli. 4 p.
- C
- \vec{F}_4 painovoima
- \vec{F}_2 ilmanvastus
4.2 Heiton jälkeen jään pinnalla liukuva curling-kivi. 5 p.
- A
- \vec{F}_3 kitka
- \vec{F}_5 jään tukivoima
- \vec{F}_6 painovoima
4.3 Uimarin selkään hihnalla kiinnitetty, vedessä liikkuva uimapoiju. 6 p.
- C
- \vec{F}_1 hihnan jännitysvoima
- \vec{F}_3 veden vastusvoima
- \vec{F}_4 noste
- \vec{F}_5 painovoima
Pisteytys:
Oikean kuvion valinta (2 p.).
Jokainen oikein nimetty voiman symboli (1 p.) riippumatta voimakuvion valinnasta.
Tyypillisiä virheitä:
Osatehtävässä 4.3 on nimetty hihnan vetovoima uimarin aiheuttamaksi voimaksi.
On väitetty painovoiman olevan nuolen, kiven tai poijun painovoima, vaikka kyseessä on Maan painovoima.
5. Eksoplaneetan kiertoaika 15 p.
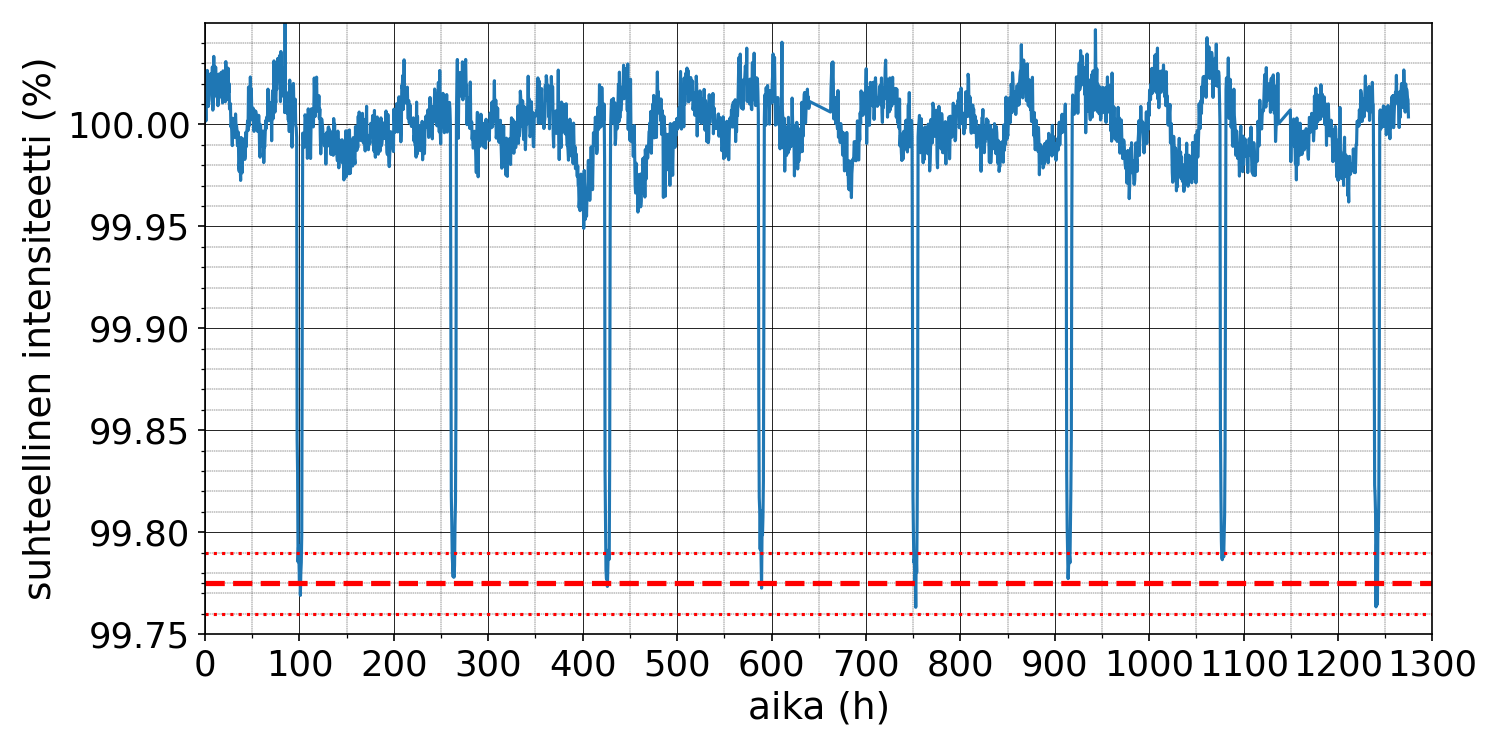
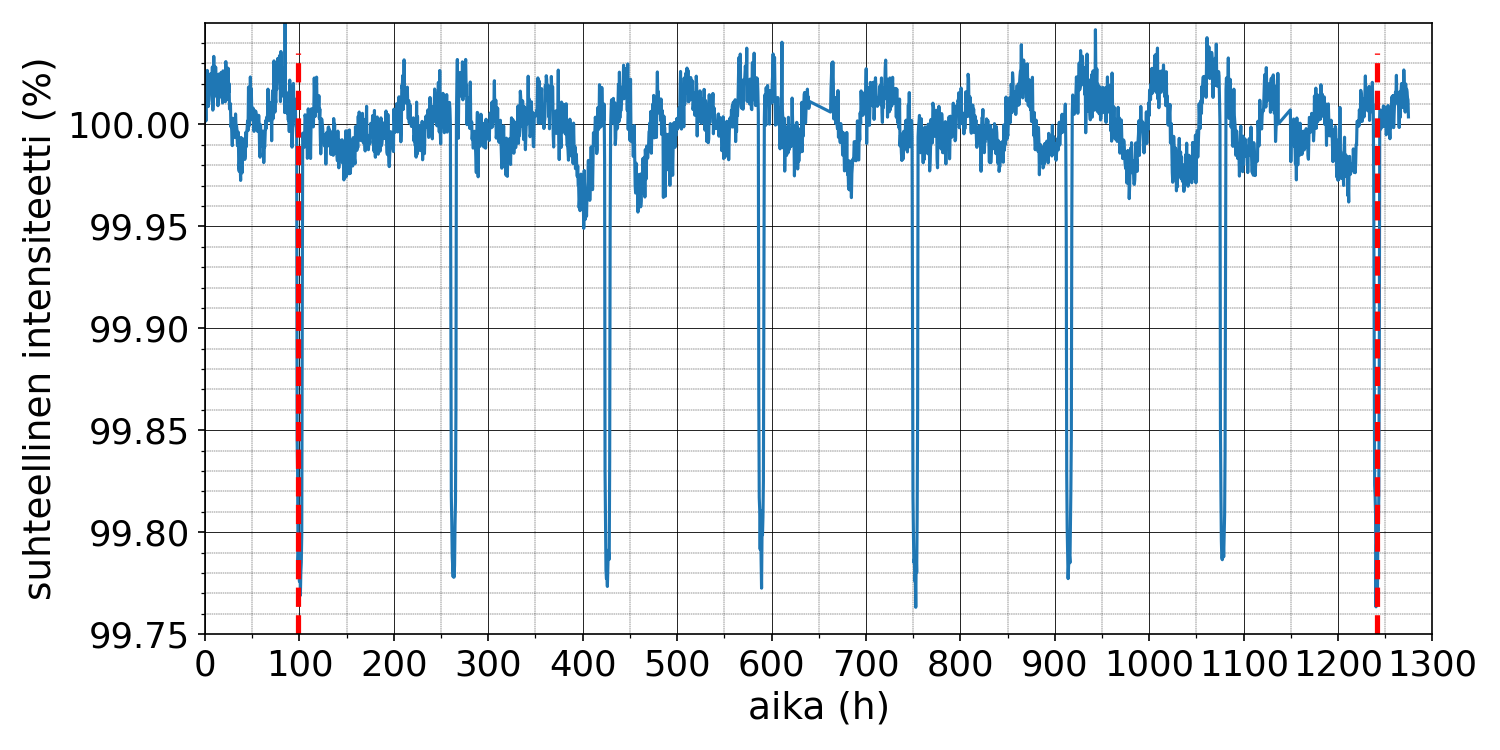
5.1 Kuvassa on esitetty erään tähden valon suhteellisen intensiteetin ajallinen vaihtelu Kepler-satelliitin mittaamana. Kuinka monta prosenttia tähden pinta-alasta planeetta enimmillään peittää? 3 p.
Pisteytys:
On annettu oikea vastaus 2–3 merkitsevän numeron tarkkuudella välillä 0,210 % - 0,245 % (3 p.).
Muusta tarkkuudesta vähennetään yksi piste.
5.2 Määritä kuvan avulla tähteä kiertävän eksoplaneetan kiertoaika. 4 p.
Pisteytys:
Ratkaisussa kiertoaika on määritetty käyttämällä useampaa kuin kahta peräkkäistä peittotapahtumaa (2 p.).
On annettu 2–3 merkitsevän numeron tarkkuudella oikea vastaus välillä 160 h – 164 h (2 p.).
Muusta tarkkuudesta vähennetään yksi piste.
Tyypillisiä virheitä:
Kiertoaika on määritetty vain kahta vierekkäistä peittotapahtumaa käyttäen.
Kiertoajan laskussa on useaan kiertoon kulunut aika jaettu piikkien lukumäärällä sen sijaan, että olisi jaettu välien lukumäärällä.
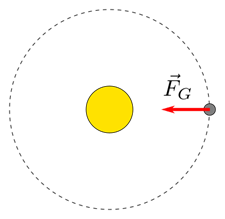
5.3 Täydennä eksoplaneetan voimakuvio kuvaan tai vastaavaan itse piirtämääsi kuvaan. Liitä kuvakaappaus vastaukseesi. Eksoplaneetan kiertorata on likimain ympyrä. Laske ympyräradan säde, kun tähden massa on 1,52 kertaa Auringon massa. 8 p.
Ympyräradalla kulkevaan eksoplaneettaan vaikuttaa vain tähden gravitaatiovoima \vec{F}_G
Newtonin II lain mukainen liikeyhtälö on voimakuvion perusteella
\frac{GMm}{r^2}=\frac{mv^2}{r}jossa M on tähden massa, m on planeetan massa, r on radan säde, G on gravitaatiovakio ja v on ratanopeus.
Planeetan ratanopeus kiertoajan T avulla lausuttuna on v=2\pi r/T, jonka sijoittaminen liikeyhtälöön tuottaa radan säteen lausekkeeksi
r=\sqrt[3]{\frac{GMT^2}{4\pi^2}}ja radan säteeksi r = 1,21\cdot 10^{10}\,{\rm m}.
Pisteytys:
Voimakuviossa eksoplaneettaan on piirretty vain gravitaatiovoimaksi nimetty voimavektori, joka osoittaa emotähden suuntaan (2 p.).
Jos voimavektori on irti eksoplaneetasta tai eksoplaneettaan on piirretty kiinni muita vektoreita, voimakuviosta annetaan 0 p.
On esitetty eksoplaneetan oikea liikeyhtälö (2 p.).
On esitetty radan säteelle ratkaistu oikea suureyhtälö (2 p.).
On annettu radan säteelle 2-3 merkitsevän numeron tarkkuudella oikea vastaus välillä 1,19 \cdot 10^{10} {\rm m} – 1,22 \cdot 10^{10} {\rm m} (2 p.). Väärästä tarkkuudesta vähennetään yksi piste.
Tyypillisiä virheitä:
Voimakuviossa eksoplaneettaan on piirretty kiinni kiihtyvyys- tai nopeusvektori.
On piirretty tähteen vaikuttava gravitaatiovoima.
6. Pölyhiukkanen kondensaattorissa 15 p.
6.1 Kuinka suuri on sähkökentän voimakkuus levyjen välissä, ja minkä suuntainen se on? 4 p.
Pisteytys:
On esitetty oikea sähkökentän suunta (2 p.).
On annettu sähkökentän voimakkuudelle 2–3 merkitsevän numeron tarkkuudella oikea vastaus 13,8 {\rm kV/m} (2 p.). Väärästä tarkkuudesta vähennetään yksi piste.
6.2 Kuinka suuri on pölyhiukkaseen kohdistuva sähköinen voima? 3 p.
Pisteytys:
On esitetty hiukkaseen vaikuttavan voiman suureyhtälö (2 p.).
On annettu voiman suuruudelle 2–3 merkitsevän numeron tarkkuudella oikea vastaus 78,9 {\rm nN} (1 p.). Väärästä tarkkuudesta vähennetään yksi piste.
6.3 Tarkastellaan vain hiukkaseen vaikuttavaa sähköistä voimaa. Millaista hiukkasen liike on? Kuinka pitkä aika hiukkaselta kuluu matkaan kondensaattorin negatiivisesti varautuneelle levylle, kun hiukkanen lähtee levosta? 8 p.
Sähkökenttä on homogeeninen, joten hiukkaseen kohdistuu vakiovoima ja hiukkasen liike on Newtonin II lain nojalla tasaisesti kiihtyvää.
Hiukkasen kiihtyvyys on a=F/m=QE/m=QU/(dm) ja sen ajassa t kulkema matka on d=\tfrac{1}{2}at^2. Ratkaisemalla yhtälöstä aika saadaan t=\sqrt{2d/a}=\sqrt{2d^2 m/(QU)} = 0,466290575\,{\rm s} \approx 0,47\,{\rm s}.
Pisteytys:
On tunnistettu, että hiukkanen on tasaisesti kiihtyvässä liikkeessä (2 p.).
Tasaisesti kiihtyvä liike on perusteltu sillä, että hiukkaseen vaikuttava voima on vakio (2 p.).
On esitetty oikea suureyhtälö ajalle (2 p.).
On annettu ajalle 2-3 merkitsevän numeron tarkkuudella oikea vastaus 0,466\,{\rm s} (2 p.). Väärästä tarkkuudesta vähennetään yksi piste.
Tyypillisiä virheitä:
Jätetään mainitsematta, että hiukkasen kiihtyvä liike on tasaisesti kiihtyvää.
Ratkaisussa ei perustella, että hiukkaseen vaikuttaa vakiovoima.
7. Leijulauta 15 p.
Vuonna 1989 ilmestyneessä Paluu tulevaisuuteen II -elokuvassa päähenkilö Marty McFly matkustaa aikakoneella tulevaisuuteen vuoteen 2015. Marty käyttää tulevaisuuden kaupungissa liikkumiseen leijulautaa.
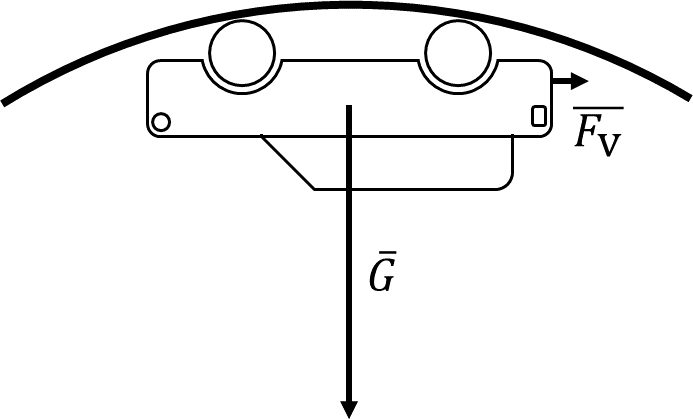
Vuonna 2015 esiteltiin leijulaudan prototyyppi, jolla voi leijailla kuparilattian päällä (kuva ). Leijulaudan sisällä olevat moottorit pyörittävät kestomagneetteja.
7.1 Miksi leijulaudan pyörivät magneetit mahdollistavat leijumisen kuparilattian päällä? 6 p.
Pisteytys:
Ratkaisussa on tunnistettu muuttuva magneettivuo (2 p.).
Esitetty, että kuparilattiaan indusoituu pyörrevirtoja (2 p.).
Ratkaisussa on perusteltu, että pyörrevirtojen synnyttämän magneettikentän ja laudan magneettien välinen vuorovaikutus on hylkivä (2 p.).
Tyypillinen virhe:
Ratkaisussa käsitelty magneettisen vuorovaikutuksen sijasta sähköstaattista vuorovaikutusta.
7.2 Miksi leijuminen ei onnistu asfaltin päällä? 3 p.
Pisteytys:
On perusteltu, ettei pyörrevirtoja muodostu, sillä ettei asfaltti ei ole sähkönjohde (3 p.).
7.3 Mitä voimia lautaan vaikuttaa kuvan tilanteessa? 3 p.
Pisteytys:
Jokaisesta oikein nimetystä voimasta annetaan yksi piste.
Tyypillinen virhe:
On esitetty, että lautailijan paino kohdistuu leijulautaan tai ei ole eritelty laudan ja lautailijan painoa.
7.4 Miksi lattia lämpenee, vaikka lauta ei kosketa lattiaa? 3 p.
Pisteytys:
On perusteltu, että kuparin resistiivisyyden takia pyörrevirrat aiheuttavat lattian lämpenemisen (3 p.).
Tyypillinen virhe:
Väitetty pyörrevirtojen lämmittävän lattiaa mainitsematta materiaalin resistiivisyyttä.
8. Ydinvoimalaitos Olkiluoto 3 15 p.
Olkiluoto 3 on ydinvoimalaitos Suomen länsirannikolla. Se tuottaa sähköä 1 600 MW:n teholla, ja sähköntuotannon hyötysuhde on 0,375. Käyttösuunnitelman mukaan laitos käy täydellä teholla yhtämittaisesti 330 vuorokautta vuodessa. Noin kuukauden kestävän käyttökatkon aikana laitosta huolletaan ja 32 tonnia käytettyä polttoainetta korvataan tuoreella polttoaineella seuraavaa käyttöjaksoa varten.
Ydinvoimalaitoksen energiantuotanto perustuu uraanin fissioreaktioon, jossa uraaniydin halkeaa kahdeksi keskiraskaaksi ytimeksi. Kussakin fissioreaktiossa vapautuu keskimäärin 0,20 GeV energiaa, jolla tuotetaan höyryä. Höyry pyörittää turbiinia ja turbiini generaattoria, joka tuottaa sähköenergiaa.
8.1 Kuinka monta fissioreaktiota tapahtuu sekunnissa Olkiluoto 3 -ydinvoimalaitoksessa, kun se käy täydellä teholla? 4 p.
Fissiot tuottavat lämpötehoa, joka saadaan tunnetusta sähkötehosta hyötysuhteen avulla: \eta=P_{\rm e}/ P_{\rm th}\Rightarrow P_{\rm th}= P_{\rm e}/\eta.
Fissioiden lukumäärä sekunnissa saadaan jakamalla lämpöteho yhdessä fissiossa vapautuvalla energialla:
x = Pth / Efissio = Pe / (η Efissio) = 1600 MW / (0,375 · 0,20 GeV · 1,6021765 · 10-19 J/eV) = 1,3315 · 1020 / s ≈ 1,33 · 1020 / s.
Pisteytys:
Ratkaisussa on esitetty idea reaktorin tehon jakamisesta yhdessä reaktiossa vapautuvan energian määrällä (2 p.).
On annettu fissioreaktioiden lukumäärän oikea vastaus 2–3 merkitsevän numeron tarkkuudella (2 p.). Väärästä tarkkuudesta vähennetään yksi piste.
Tyypillinen virhe:
Ratkaisussa on jätetty voimalan hyötysuhteen vaikutus huomiotta.
8.2 Kuinka paljon polttoaineen massaa katoaa fissioreaktioiden takia vuodessa, kun laitos toimii käyttösuunnitelman mukaisesti? 4 p.
Energian ja massakadon yhteys on: E = mc2, josta m = E/c2.
Vuoden aikana fissioiden tuottama lämpöenergia saadaan kertomalla teho käyttöajalla:
E = Pth T = Pe T / η.
Näin ollen massan muutos vuoden aikana on
m = Pe T / (η c2) = 1600 MW · 330 d · 24 h/d · 3600 s/h / (0,375 · (3 · 108 m/s)2) = 1,3517 kg ≈ 1,4 kg.
Pisteytys:
Ratkaisussa on käsitelty oikein massakadon ja energian välinen yhteys (2 p.).
On annettu massalle 2-3 merkitsevän numeron tarkkuudella oikea arvo 1,35\,{\rm kg} (2 p.). Väärästä tarkkuudesta vähennetään yksi piste.
Tyypillisiä virheitä:
Ratkaisussa on jätetty voimalaitoksen hyötysuhde huomiotta.
Ratkaisussa on oletettu voimalaitoksen olevan toiminnassa 365 päivää vuodessa tehtävänannossa annetun 330 päivän sijaan.
8.3 Jos saman sähkötehon tuottamiseen käytetään kivihiilivoimalaitosta, tarvittavan kivihiilen massa on 100 000-kertainen uraanipolttoaineen massaan verrattuna. Mistä tämä ero johtuu? 4 p.
Kivihiilen polttamisen yhteydessä energiaa vapautuu hiiliatomin yhtyessä happeen, kun taas uraanin fissiossa energiaa vapautuu atomiytimen haljetessa. Palamisreaktiossa vapautuva energia liittyy molekyylien sidosten katkeamisiin ja muodostumisiin (sähkömagneettinen vuorovaikutus) ja se on reaktiota kohti eV-luokkaa. Fissioreaktiossa energiaa vapautuu nukleonien uudelleenjärjestymisestä (vahva vuorovaikutus) ja se on reaktiota kohti MeV-luokkaa. Uraanipolttoaineen ytimistä tyypillisesti vain muutama prosentti fissioituu käytön aikana, mutta siitä huolimatta palamisreaktioita ja hiilipolttoainetta tarvitaan 5–6 suuruusluokkaa enemmän kuin ydinreaktioita ja ydinpolttoainetta.
Pisteytys:
On tunnistettu, että palamisreaktiossa on kyse sähkömagneettisesta vuorovaikutuksesta tai kemiallisen energian vapautumisesta ja fissioreaktiossa on kyse vahvasta vuorovaikutuksesta tai nukleonien sidosenergian vapautumisesta (2 p.).
On perusteltu, että yhdessä ydinreaktiossa vapautuvan energian määrä on paljon suurempi kuin yhdessä kemiallisessa reaktiossa vapautuvan energian määrä. (2 p.).
8.4 Hiilivoima ja ydinvoima aiheuttavat käytön aikana ympäristölle haittoja ja riskejä. Kuvaile kolme merkittävää eroa hiilivoimalan ja ydinvoimalan välillä käytön aikaisissa haitoissa ja riskeissä. 3 p.
Merkittävimmät erot hiilivoiman ja ydinvoiman haittojen ja riskien välillä laitosten käytön aikana:
- Hiilidioksidi: Hiilivoimalaitos tuottaa käytön aikana hiilidioksidia, ydinvoimalaitos ei juurikaan.
- Pienhiukkaset: Hiilivoimalaitos tuottaa käytön aikana pienhiukkasia, ydinvoimalaitos ei.
- Onnettomuusriski: Ydinvoimalaitoksessa on käytön aikana suuria määriä radioaktiivisia aineita, jotka aiheuttavat säteilyonnettomuuden riskin. Hiilivoimalaitoksessa ei käytetä radioaktiivisia aineita.
Pisteytys:
Jokaisesta oikeasta eroavaisuudesta, jossa on käsitelty molempia voimaloita ja esitetty oikein niiden ero (1 p.).
Tyypillisiä virheitä:
Vastauksessa on käsitelty vain yhtä voimalatyyppiä vertaamatta sitä toiseen.
On vertailtu muita kuin käytön aikaisia erovaisuuksia.
Osa 3: 20 pisteen tehtävät
9. Aurinkovoimala 20 p.
9.1 Aurinkopaneelien energiantuotanto riippuu kellonajasta. Ilmeisin tähän vaikuttava asia on se, että elokuussa aurinko nousee kello 5:n aikoihin ja laskee kello 22:n aikoihin. Mainitse kolme muuta asiaa, jotka vaikuttavat siihen, että energiantuotanto muuttuu vuorokauden mittaan. 3 p.
- Pilvet varjostavat paneeleita, ja auringon valo absorboituu pilviin tai siroaa niistä muualle. Tämä näkyy tuotannon nopeina muutoksina.
- Auringon ja paneeleiden välinen kulma muuttuu vuorokaudenajan mukaan. Maksimin paikka ei ole kello 13, joten paneelit on suunnattu länteen. Tällöin auringon säteily osuu paneeleihin paremmin vasta iltapäivällä.
- Puut ja rakennukset varjostavat paneeleita, joten ne ovat varjossa tiettyihin aikoihin päivässä. Esimerkiksi kello 14.30–15.00 kaikissa käyrissä on hetkellinen minimi, joka saattaa syntyä tällaisesta varjosta.
- Auringon paistaessa pitkään paneelien lämpötila nousee ja tuotanto laskee. Paneelien hyötysuhde heikkenee lämpötilan kasvaessa noin 4 % kymmentä Kelviniä kohti.
Pisteytys:
Jokainen oikea asia (1 p.).
Tyypillinen virhe:
Esitetty energiantuotantoon liittyviä väitteitä, jotka eivät vastaa kysymykseen tuotannon muuttumisesta vuorokauden mittaan.
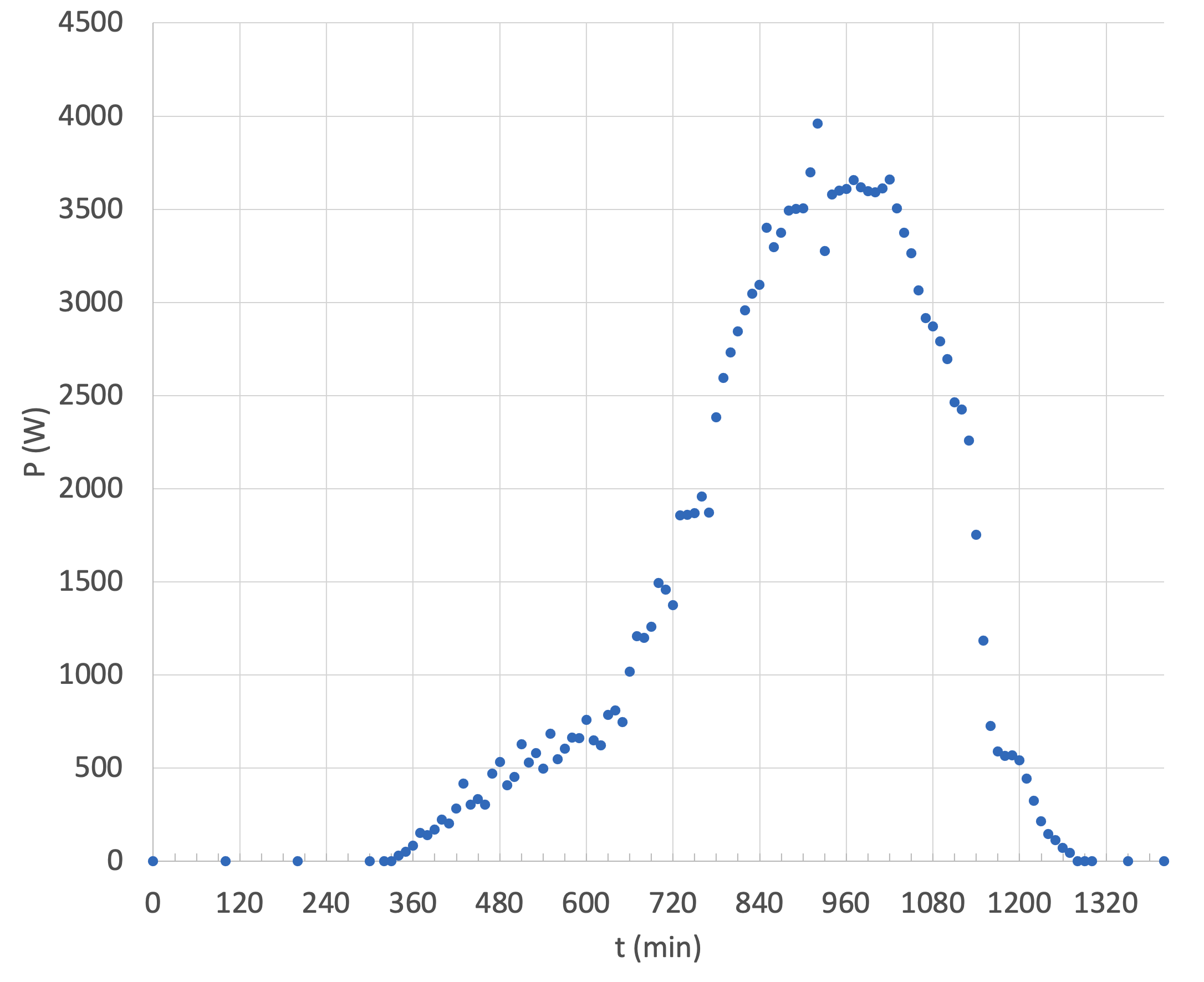
9.2 Kuinka paljon energiaa tällä pienvoimalalla pystyisi enimmillään tuottamaan yhdessä vuorokaudessa elokuun alussa? Laadi taulukon perusteella sopiva graafinen esitys, josta määrität enimmillään tuotettavissa olevan energian. 9 p.
Valitaan mittausaineistosta kunkin ajankohdan suurin mitattu teho ja muodostetaan näistä oma sarake tiedostoon. Piirretään näin saatu aika-tehokuvaaja. Se vastaa pilvettömän päivän energiantuottoa.
Vuorokaudessa tuotettua energiaa kuvaa käyrän alle jäävä pinta-ala, joka on 1 550 000 W · min tai 25,9 kWh tai 93,2 MJ.
Pisteytys:
Ratkaisusta käy ilmi, että käytetään kunkin ajankohdan suurinta tehoa (2 p.).
On esitetty kuvaaja, jossa näkyy maksimiteho kellonajan tai keskiyöstä mitatun ajan funktiona. (3 p.).
Ratkaisusta käy selvästi ilmi, että energia saadaan käyrän alle jäävästä pinta-alasta (2 p.).
On annettu vastauksena 1–3 merkitsevän numeron tarkkuudella energia 25 kWh – 28 kWh tai 90 MJ – 100 MJ (2 p.). Muusta tarkkuudesta vähennetään 1 piste.
Tyypillinen virhe:
Käytetään vain yhden päivän kuvaajaa tai viiden päivän keskiarvoa.
9.3 Mihin aikaan päivästä ja kuinka pitkällä aikavälillä paneelien energiantuotanto olisi suurimmillaan osatehtävän 9.2 mukaisessa ideaalitilanteessa? 4 p.
Käytetään osion 9.2 graafista esitystä tai piirretään mittausaineisto kultakin päivältä samaan kuvaan. Niistä voidaan päätellä, että suurin teho saavutetaan noin 90 minuutin ajan iltapäivällä 940 minuuttia keskiyöstä eli noin kello 15.00–16.30. Käyrän maksimin alue on mahdollisesti tätäkin laajempi.
Pisteytys:
On annettu vastauksena suurimman tehon ajankohta väliltä 14.10 – 17.30 (2 p.).
On annettu vastauksena graafisen esityksen avulla perusteltu aikavälin pituus väliltä 60 min – 200 min (2 p.).
Tyypillinen virhe:
Jätetty graafinen esitys näyttämättä tai jätetty viittaamatta siihen millään tavalla
9.4 Valmistajan antamien tietojen mukaan aurinkopaneelit pystyvät muuttamaan 19 % niihin osuvasta auringon säteilyenergiasta sähköenergiaksi. Mainitse kaksi seikkaa, jotka vaikuttavat siihen, että kaikkea paneeleihin osuvaa säteilyenergiaa ei voida muuttaa sähköenergiaksi. 4 p.
- Osa tulevasta säteilystä heijastuu paneelin pinnasta.
- Jotta paneeli pystyisi tuottamaan säteilystä sähköä, säteilykvantin energian tulee ylittää paneelin puolijohdemateriaalin kynnysenergia. Kynnysenergiaa vastaavaa aallonpituutta pitkäaaltoisempi säteily ei absorboidu paneeleihin eikä siten tuota sähköä. Auringosta tulevasta säteilystä merkittävä osa (noin neljäsosa) on infrapunasäteilyn alueella, eikä näiden kvanttien energia riitä sähkön tuottamiseen.
- Energian luovuttaminen on kahden hiukkasen välinen prosessi. Kennoon absorboituva fotoni luovuttaa energiansa yhdelle elektronille. Kun fotonin energia on suurempi kuin kynnysenergia, kenno ei pysty käyttämään hyväkseen fotonin koko energiaa vaan ainoastaan tarvitsemansa kynnysenergian. Näin lyhytaaltoisemman säteilyn kaikkea energiaa ei pystytä käyttämään hyväksi. Auringosta tulevasta säteilystä merkittävä osa (noin neljäsosa) on ultraviolettialueella, ja näiden kvanttien energiasta merkittävä osa jää ylimääräiseksi.
Pisteytys:
Ratkaisussa on tunnistettu heijastuminen (2 p.) tai kerrottu kvantin tarvitsemasta minimienergiasta (2 p.) tai kerrottu osan kvantin energiasta menevän hukkaan (2 p.), kuitenkin niin, että yhteensä annetaan vain neljä pistettä.
Tyypillinen virhe:
Väitetty energian heijastuvan.
10. Autorata 20 p.
10.1 Auto kulkee autoradan korkeimmassa kohdassa ylösalaisin mutta pysyy radalla. Mikä on sen pienin mahdollinen nopeus tässä kohdassa? 6 p.
Newton II lain mukaan y-suuntaisille voimille radan korkeimmassa kohdassa pätee G-N = ma_{\rm n}, jossa a_{\rm n}, auton normaalikiihtyvyys on suurimman silmukan keskipistettä kohti. Nopeus on pienimmillään rajatapauksessa, jossa N = 0 jolloin G = m a_{\rm n}.
Normaalikiihtyvyys on a_{\rm n} = v^2/r ja auton paino G = mg, joten mg = m v^2/r, josta saadaan pienin mahdollinen nopeus v=\sqrt{gr}=\sqrt{9,81\,\frac{\rm m}{{\rm s}^2}\cdot \frac{0,51}{2}\,{\rm m}}=1,581629\,{\rm m/s} \approx 1,6\,{\rm m/s}.
Pisteytys:
Ratkaisussa on mainittu normaalivoiman häviävän rajatapauksessa (2 p.),
kirjoitettu auton liikeyhtälö suuresymboleilla (2 p.) ja annettu 2–3 merkitsevän numeron tarkkuudella oikea vastaus (2 p.). Muusta tarkkuudesta vähennetään yksi piste.
Tyypillinen virhe:
Ei kerrota normaalivoiman olevan rajatapauksessa nolla.
10.2 Auto lähetetään radalle nopeudella 3,1 m/s. Radan läpi kulkenut auto lennähtää hyppyristä 32 cm:n korkeuteen ja laskeutuu takaisin radan tasolle 15 cm:n etäisyydelle lentoradan korkeimmasta kohdasta (kuva ). Autoon ilmalennon aikana kohdistuvat vastusvoimat voidaan olettaa merkityksettömiksi, joten hypyn aikana auton nopeuden vaakasuora komponentti pysyy vakiona, mutta pystysuora komponentti muuttuu tasaisesti. Kuinka suuri oli autoon kohdistuvien vastusvoimien tekemä työ koko radan matkalla? 7 p.
Mekaniikan energiaperiaatteen mukaan E_{p1}+ E_{k1}+W= E_{p2}+ E_{k2}, jossa W on vastusvoimien tekemä työ. Auton mekaaninen energia on alussa E_{p1}=0 ja E_{k1}=\tfrac{1}{2}mv_0^2 ja lopussa E_{p2}=mgh ja E_{k2}=\tfrac{1}{2}mv^2, joten energiaperiaatteesta saadaan yhtälö \tfrac{1}{2}mv_0^2-W = mgh+\tfrac{1}{2}mv^2, jolloin W=m(\tfrac{1}{2}v_0^2-gh-\tfrac{1}{2}v^2).
Auton nopeus hypyn aikana voidaan laskea auton putoamisliikkeen avulla. Auto putoaa pystysuoran matkan h samalla kun se etenee vaakasuoran matkan x. Lakipisteessä y-suuntainen nopeus on nolla, jolloin h=\tfrac{1}{2}gt^2, josta saadaan auton putoamiseen kuluva aika t=\sqrt{2h/g}. Lakipisteestä auto etenee vaakasuuntaan x=vt, jolloin auton nopeus v = x/\sqrt{2h/g} = 0,15\,{\rm m}/\sqrt{2\cdot 0,32\,{\rm m}/(9,81\,{\rm m/s}^2)} = 0,587267\,{\rm m/s}. Vastusvoimien tekemä työ on tällöin W=m(\tfrac{1}{2}v_0^2-gh-\tfrac{1}{2}v^2) = 0,037\,{\rm kg}\cdot \Bigl( \tfrac{1}{2}\cdot\bigl( 3,1\,\tfrac{\rm m}{\rm s}\bigr)^2 -9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot 0,32\,{\rm m} -\tfrac{1}{2}\cdot \bigl( 0,587267\,\tfrac{\rm m}{\rm s}\bigr)^2\Bigr) = 0,0552543\,{\rm J} \approx 0,055\,{\rm J}.
Pisteytys:
Ratkaisu on sanallisesti perusteltu mekaniikan energiaperiaatteella (1 p.).
On kirjoitettu oikea suureyhtälö auton nopeudelle joko hypyn lakipisteessä tai lopussa, tai ratkaistu kyseinen nopeus oikein (2 p.).
On kirjoitettu oikea suureyhtälö vastusvoimien tekemälle työlle (2 p.) ja annettu 1–3 merkitsevän numeron tarkkuudella oikea vastaus (2 p.) joko positiivisena tai negatiivisena. Muusta tarkkuudesta vähennetään yksi piste.
Tyypillinen virhe:
Unohdettu auton liike-energia lakipisteessä.
10.3 Eri leikkiautot toimivat radalla hieman eri tavalla. Valitaan leikkiauto, jonka alkuvauhti ja vastusvoimat ovat sellaiset, että auto ohittaa ensimmäisen ja toisen silmukan korkeimmat kohdat pienimmillä mahdollisilla nopeuksilla. Pääseekö leikkiauto myös kolmannen silmukan läpi? Voit olettaa, että autoon vaikuttavat vastusvoimat ovat keskimäärin yhtä suuria radan kaikissa silmukoissa. 7 p.
Radan ja auton välinen tukivoima on nolla, jos auto liikkuu pienimmillä mahdollisella nopeudella, jolloin y-suuntaiset voimat kahden ensimmäisten silmukan korkeimmissa kohdissa noudattavat samaa ehtoa kuin osatehtävässä 10.1, eli G=ma_n. Tästä saadaan v_n=\sqrt{gr_n}.
Mekaaninen kokonaisenergia eri silmukoiden lakipisteissä on tällöin
- ensimmäisen silmukan kohdalla mgd_1+\tfrac{1}{2}mv_1^2=mgd_1+\tfrac{1}{2}mgr_1=E_1,
- toisen silmukan kohdalla mgd_2+\tfrac{1}{2}mv_2^2=mgd_2+\tfrac{1}{2}mgr_2=E_2.
Auton mekaaninen kokonaisenergia ensimmäisen silmukan lakipisteessä on E_1=mgd_1+\tfrac{1}{2}mgr_1=0,037\,{\rm kg}\cdot 9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot (0,51\,{\rm m}+\tfrac{1}{2}\cdot \tfrac{0,51\,{\rm m}}{2}) = 0,23139338\,{\rm J}.
Toisen silmukan lakipisteessä kokonaisenergia on vähentynyt vastusvoimien tekemän työn verran, W=-F\Delta x_1, jolloin E_2=mgd_2+\tfrac{1}{2}mgr_2=E_1-F\Delta x_1, jossa radan pituus ensimmäisen ja toisen silmukan lakipisteiden välillä on \Delta x_1 = \tfrac{1}{2}2\pi r_1+\tfrac{1}{2}2\pi r_2=\tfrac{1}{2}\pi(d_1+d_2) = \tfrac{1}{2}\pi(0,51\,{\rm m}+0,38\,{\rm m})=1,3980087\,{\rm m}.
Keskimääräiseksi vastusvoimaksi saadaan F=\frac{1}{\Delta x_1}(E_1-mgd_2-\tfrac{1}{2}mgr_2)=0,042190455\,{\rm N}.
Kolmannen silmukan kohdalla energia on edelleen vähentynyt vastusvoimien matkalla \Delta x_2 tekemällä työllä, eli kokonaisenergia kolmannen silmukan lakipisteessä on E_3=E_1-F\Delta x_1-F\Delta x_2=E_1-F(\Delta x_1+\Delta x_2), jossa etäisyys toisen ja kolmannen silmukan lakipisteiden välillä on \Delta x_2=\tfrac{1}{2}2\pi r_2+\tfrac{1}{2}2\pi r_3=\tfrac{1}{2}\pi(d_2+d_3) = \tfrac{1}{2}\pi(0,38\,{\rm m}+0,25\,{\rm m})=0,98960169\,{\rm m}.
Mekaaninen kokonaisenergia on tällöin E_3=E_1-F(\Delta x_1+\Delta x_2)=0,13065900\,{\rm J}.
Leikkiauto pääsee kolmannenkin silmukan läpi, jos sen nopeus lakipisteessä ylittää pienimmän mahdollisen nopeuden, eli v_n=\sqrt{gr_n}. Siten mekaanisen kokonaisenergian pitää olla vähintään E_{\rm min}=mgd_3+\tfrac{1}{2}mgr_3=0,037\,{\rm kg}\cdot 9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot \bigl(0,25\,{\rm m}+\tfrac{1}{2}\cdot \tfrac{0,25\,{\rm m}}{2}\bigr)=0,11342813\,{\rm J}.
Tässä tapauksessa energia ylittää vähimmäisenergian, eli E_3 > E_{\rm min}, joten leikkiauto pääsee läpi kolmannestakin silmukasta.
Pisteytys:
On ilmaistu, että tarvitaan mekaanisten energioiden (E_{\rm 1}) ja (E_{\rm 2}) erotus silmukoiden 1 ja 2 korkeimmassa kohdassa (1 p.).
On kirjoitettu oikeat suureyhtälöt energioille E_{\rm 1} ja E_{\rm 2} tai laskettu niiden suuruudet (1 p.).
On kirjoitettu oikea suureyhtälö keskimääräiselle vastusvoimalle tai laskettu sen suuruus (2 p.).
On kirjoitettu oikea suureyhtälö mekaaniselle energialle E_{\rm 3} tai sitä vastaavalle nopeudelle kolmannen silmukan korkeimmassa kohdassa (1 p.).
On annettu oikein perusteltu vastaus, että auto selviää silmukasta (2 p.).
Tyypillisiä virheitä:
Unohdettu auton liike-energia tai potentiaalienergia silmukan lakipisteessä.
On oletettu, että vastusvoimien tekemä työ on yhtä suuri jokaisessa silmukassa.
11. Röntgendiffraktio ja elektronidiffraktio 20 p.
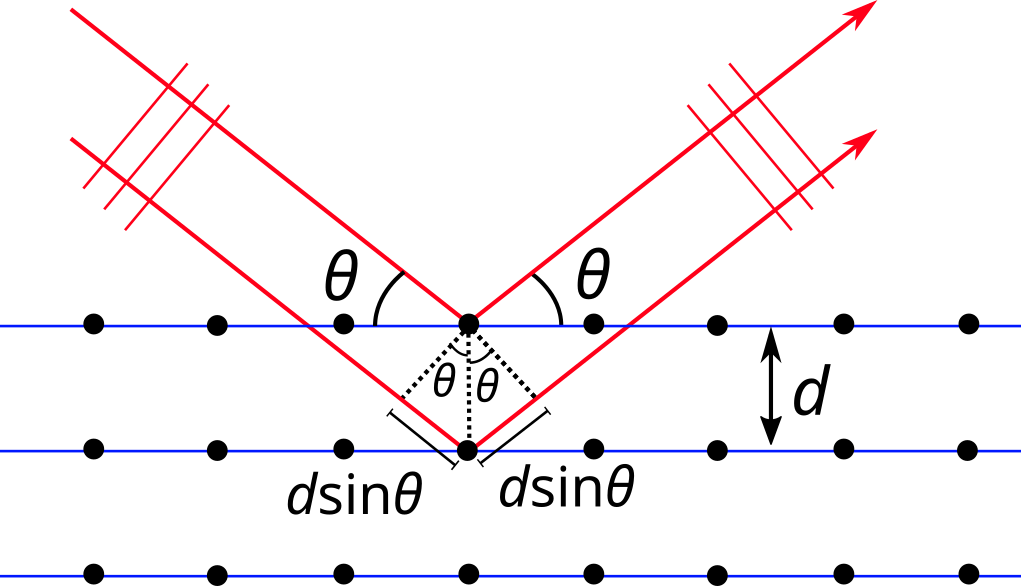
11.1 Johda aineiston kuvaa apuna käyttäen Braggin laki 2d sin θ = nλ, jossa θ on säteilyn ja atomitason välinen kulma, λ on säteilyn aallonpituus ja n on diffraktion kertaluku. 5 p.
Tutkitaan kahdesta allekkaisesta tasosta sironneita säteitä. Alemmasta tasosta sironnut säde on kulkenut pidemmän matkan kuin ylemmästä tasosta sironnut säde. Matkaero havaitaan kuvasta, kun siihen lisätään aaltorintamat sopiviin kohtiin, jolloin kahdesta suorakulmaisesta kolmiosta voidaan lukea matkaeroksi 2d sin θ. Jotta säteet (oikeastaan aaltorintamat) olisivat samassa vaiheessa, kun ne osuvat detektoriin, matkaeron tulee olla aallonpituuden monikerta, eli vaaditaan, että 2d sin θ = nλ, joka on Braggin laki.
Pisteytys:
On kuvan avulla oikein selittäen määritetty säteiden matkaero (3 p.).
On perusteltu konstruktiivisen interferenssin avulla matkaeron olevan aallonpituuden monikerta (2 p.).
Tyypillinen virhe:
Jätetty viittaamatta kuvaan tai laskettu sen avulla matkaero väärin.
11.2 Kuvassa on raudasta mitattu röntgendiffraktiokuvaaja, jossa näkyy kolme ensimmäisen kertaluvun (n = 1) intensiteettimaksimia. Mittaus tehtiin säteilyllä, jonka aallonpituus oli λ = 0,15406 nm. Mikä intensiteettimaksimeista (a, b, c) vastaa pienintä atomitasojen välistä etäisyyttä? Määritä kyseinen etäisyys. 5 p.
Braggin laista nähdään, että mitä suurempi on diffraktiokulma, sitä pienempi on d:n arvo. Pienintä atomitasojen välistä etäisyyttä vastaa intensiteettimaksimi c. Luetaan kuvan 11.B spektristä kulma θ piikille c: θ = 41,0º. Kirjoitetaan Braggin laki muotoon d = λ / (2 sin θ), kun n = 1. Sijoitetaan kulma ja aallonpituuden arvo λ = 0,15406 nm, joista saadaan tasojen väliseksi etäisyydeksi d = 0,117 nm.
Pisteytys:
On valittu perustellen maksimi c (3 p.).
On annettu 2–3 merkitsevän numeron tarkkuudella oikea vastaus (2 p.) käyttämällä kulmaa välillä 40,5˚ – 41,5˚. Muusta tarkkuudesta vähennetään 1 piste.
11.3 Eräässä röntgendiffraktiokokeessa käytetään molybdeenin niin sanottua Kα-röntgensäteilyä, jonka energia on 17,48 keV. Toisessa diffraktiokokeessa käytetään röntgensäteilyn sijasta elektroneja. Määritä elektronien nopeus prosentteina valon nopeudesta, kun elektronien de Broglien aallonpituus on yhtä suuri kuin röntgensäteilyn aallonpituus. 6 p.
Muodostetaan lauseke Kα-säteilyn aallonpituudelle. Kyseessä on fotoni, joten E = hf = hc/λ. Tästä saadaan λ = hc/E.
De Broglien aallonpituudelle pätee λ = h/p, jossa p = mv on elektronin liikemäärä. Vaaditaan, että aallonpituudet ovat samat, joten hc/E = h/(mv). Ratkaistaan nopeudeksi v = E/(mc).
Vastaus pyydettiin c:n murto-osana v/c = E/(mc²). Jos käytetään elektronin lepoenergiaa eli 511 keV, saadaan v/c = 17,48 keV / 511 keV = 0,03421 eli 3,4 % valon nopeudesta.
Tai: v/c = (17,48 · 103 · 1,6022 · 10-19 J) / (9,109 · 10-31 kg (2,998 · 108 m/s)2) = 0,03421, joten nopeus on 3,4 % valon nopeudesta.
Pisteytys:
On annettu sähkömagneettisen säteilyn aallonpituudelle oikea suureyhtälö tai lukuarvo (2 p.).
On ratkaistu nopeudelle v tai suhteelle v/c oikea suureyhtälö (2 p.).
On annettu 2–5 merkitsevän numeron tarkkuudella oikea vastaus (2 p.). Muusta tarkkuudesta vähennetään yksi piste.
Tyypillinen virhe:
Sekoitettu sähkömagneettisen säteilyn aallonpituus ja elektronin aallonpituus.
11.4 Kuinka suuri kiihdytysjännite tarvitaan elektronien kiihdyttämiseksi osatehtävässä 11.3 kysyttyyn nopeuteen? 4 p.
Elektronien nopeus on noin 3 % valonnopeudesta, joten suhteellisuusteorian mukaista tarkastelua ei tarvita. Kineettinen energia Ek = mv²/2. Elektronit kiihdytetään jännitteen U yli, jolloin ne saavat energian Ek = eU, jossa e on alkeisvaraus. Näistä saadaan eU = mv²/2, josta
U=\tfrac{mv^2}{2e}=\tfrac{E_k^2}{2emc^2}\approx 298,9\,{\rm V}.
Pisteytys:
On annettu oikea suureyhtälö kiihdytysjännitteelle (2 p.).
On annettu 1–5 merkitsevän numeron tarkkuudella oikea vastaus (2 p.). Muusta tarkkuudesta vähennetään yksi piste.