Beskrivningar av goda svar: SV – Fysik
27.3.2024
Slutgiltiga beskrivningar av goda svar 14.5.2024
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
15.5.2024 kl. 15.30 korrigerat talvärde i deluppgift 2.3, preciserat ordalydelser i deluppgifterna 5.2 och 5.3 samt tillagt ett exempel på typiska fel i uppgift 4.
Del 1: 20-poängsuppgift
1. Flervalsuppgifter från olika delområden i fysiken 20 p.
Välj det alternativ som passar bäst för varje situation i deluppgifterna. Rätt svar ger 2 p., fel svar 0 p. och inget svar 0 p.
1.1 En åttondeklassare använder mobilens tidtagarfunktion för att mäta tiden det tar att springa ett 60-meterslopp. Med vilken noggrannhet är det meningsfullt att ange slutresultatet? 2 p.
- 0,1 s (2 p.)
1.2 I vilket av följande mätresultat är det relativa felet störst? 2 p.
- 2,2 kg ± 0,2 kg (2 p.)
1.3 Vilken är storleksordningen för energiförbrukningen vid ett bastubad i en elbastu i en privat bostad? 2 p.
- 8 kWh (2 p.)
1.4 Vilket av följande färdsätt förbrukar mest energi per person och per kilometer? 2 p.
- Flygplan (2 p.)
1.5 På vilket sätt värmer atmosfärens växthusgaser jorden? 2 p.
- De absorberar strålningen från jordens yta så att atmosfären värms upp och jordens temperatur stiger. (2 p.)
1.6 För vilken typ av kraftverk har mängden elektrisk energi som produceras i Finland ökat mest under 2020-talet? 2 p.
- Vindkraftverk (2 p.)
1.7 Vilken grundväxelverkan är starkast på mycket små avstånd (< 1 fm)? 2 p.
- Stark växelverkan (2 p.)
1.8 Hur stor del av universums sammansättning består av vanlig materia som vi känner till? 2 p.
- 5 % (2 p.)
1.9 Spiralfjädern från en kulspetspenna pressas samman med en kraft på 2,5 N, varvid den blir 0,1 cm kortare. Kan man utgående från det här dra slutsatsen att den här fjäderns längd ökar med 100 cm om den dras ut med en kraft på 2 500 N? 2 p.
- Nej, eftersom fjädern inte kan dras ut så långt. (2 p.)
1.10 För att förklara observationen av ett nytt fysikaliskt fenomen skapades en modell, och modellens giltighet undersöktes experimentellt. Modellens prognos och det experimentella resultatet var motsägelsefulla. Hur bör undersökningen då framskrida? 2 p.
- Om inga uppenbara fel i utförandet av experimentet uppdagas måste den skapade modellen ändras. (2 p.)
Del 2: 15-poängsuppgifter
2. En äppeljuicepress 15 p.
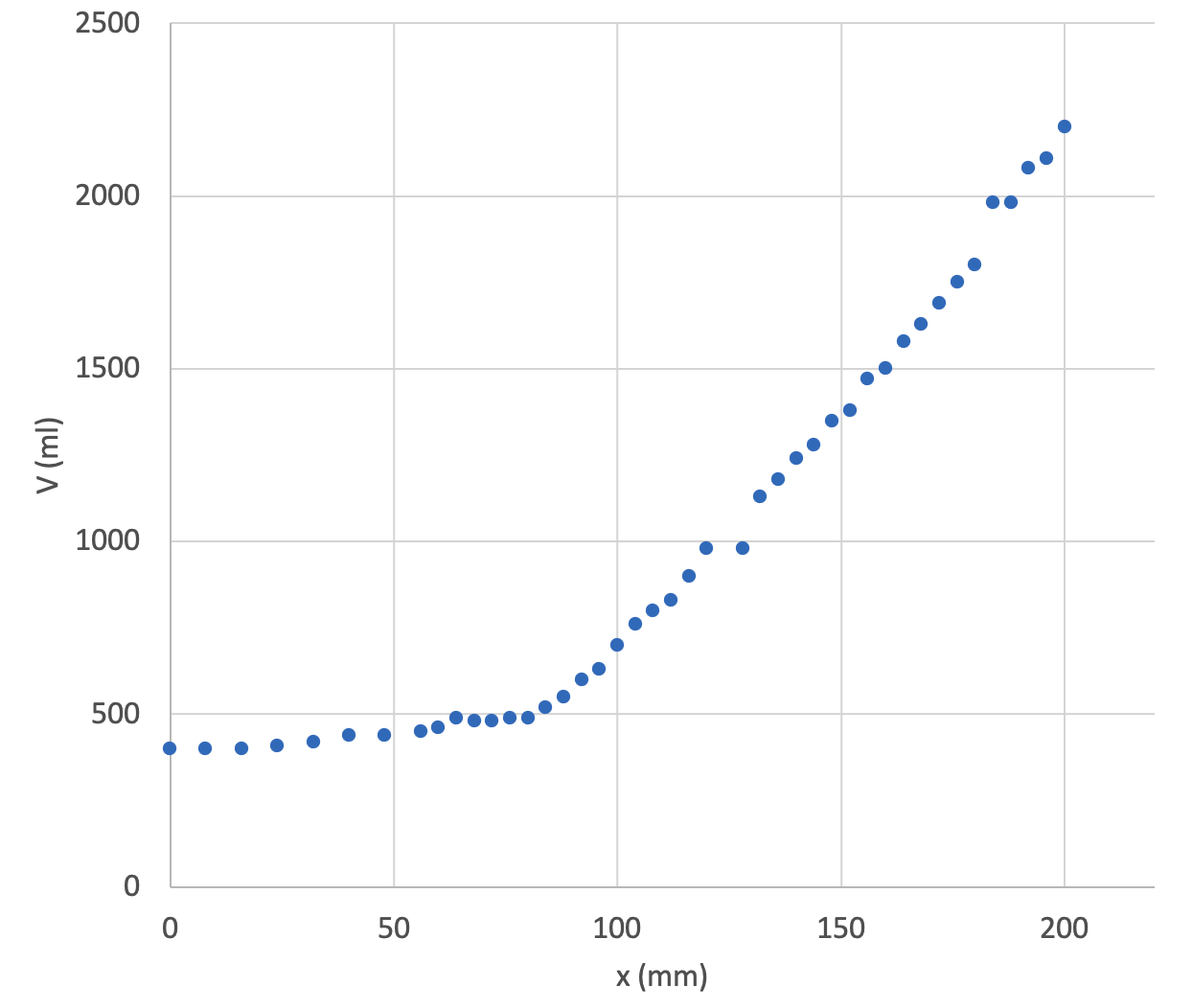
Med en äppeljuicepress (bild ) gör man juice av äpplen. Äpplena krossas och läggs i en filterpåse som placeras i metallkärlet som syns i bilden. Metallkärlets väggar är fulla av hål som juicen kan rinna ut genom. När man vrider på pressens vev trycks kolven neråt och äppelkrosset pressas.
Pressens vev vreds ett varv åt gången och volymen av juicen som rann ut mättes. Mätresultaten presenteras i material .
2.1 Presentera grafiskt volymen av juicen som funktion av sträckan kolven rört sig från sin högsta position. Ett varv med veven motsvarar en lodrät sträcka på 4,0 mm. I presentationen ska punkter som motsvarar mätresultaten synas, men inte linjer som sammanbinder punkterna. 5 p.
Med hjälp av tabellberäkning skapar vi en ny tabell där kolumnerna är sträckan som kolven rört sig från sin högsta position och juicens volym. Vi ritar en graf.
Poängsättning:
Typiskt fel:
Det har presenterats en graf där de uppmätta värdena för volymen som funktion av sträckan som kolven rört sig syns som enskilda mätpunkter. (5 p.)
Ifall att volymen har ritats som funktion av antalet varv är avdraget tre poäng.
Om mätpunkterna inte syns eller saknas är avdraget två poäng.
Om mätpunkterna är sammanlänkade med en bruten linje är avdraget en poäng.
Om endera axelns siffervärden är felaktiga eller saknas, eller om axlarna är omvända, är avdraget två poäng.
Om storhetens beteckning eller enhet saknas från endera axeln är avdraget för varje fel en poäng.
En anpassning har ritats i grafen. Det här felet har inte föranlett avdrag från poängen för grafen.
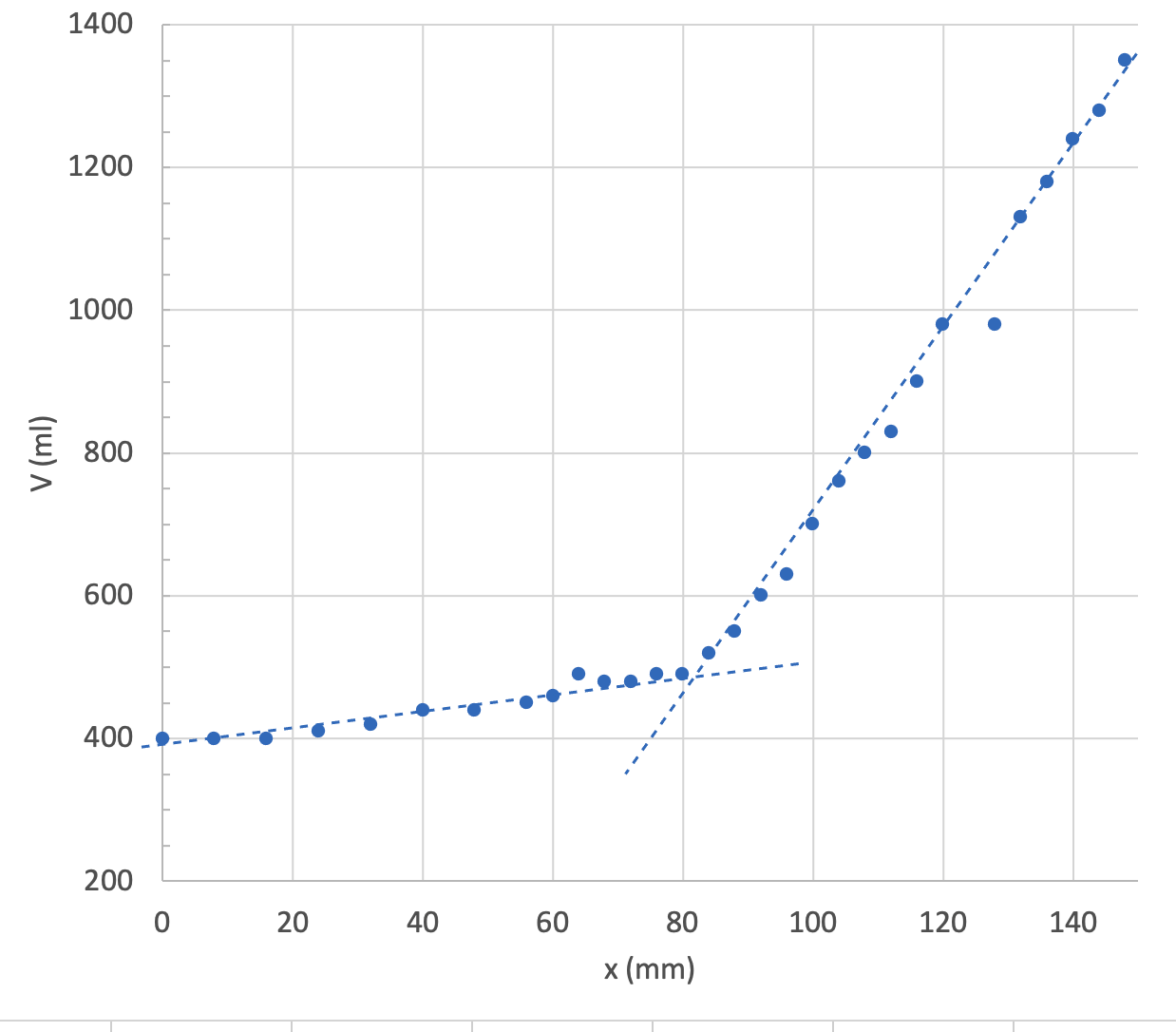
2.2 Som visat i bild måste veven vridas flera varv innan kolven når äppelkrosset. Bestäm utgående från grafen du ritade i deluppgift 2.1 hur mycket juice man fick ur äpplena innan kolven nådde ner till krosset. 4 p.
I den grafiska presentationen ser vi två delar som båda kan approximeras med en rät linje. Linjernas skärningspunkt befinner sig ungefär vid 500 ml.
Utan att pressa får vi alltså ungefär 0,5 liter juice.
Poängsättning:
Med 1–2 gällande siffrors noggrannhet har ett svar för juicens volym givits inom intervallet 490 ml – 500 ml. (2 p.) För övrig noggrannhet är avdraget en poäng.
Ifall det berättats att det gjorts ett antagande om att det ursprungligen fanns 400 ml juice i kärlet, och det har använts för att få ett svar på 90 ml -100 ml, räknas svaret som korrekt.
Mängden juice har motiverats genom att hänvisa till punkten x= 80 mm i den grafiska presentationen. (2 p.)
Typiskt fel:
Svaret har givits utan graf eller utan att hänvisa till grafen ritad i deluppgift 2.1.
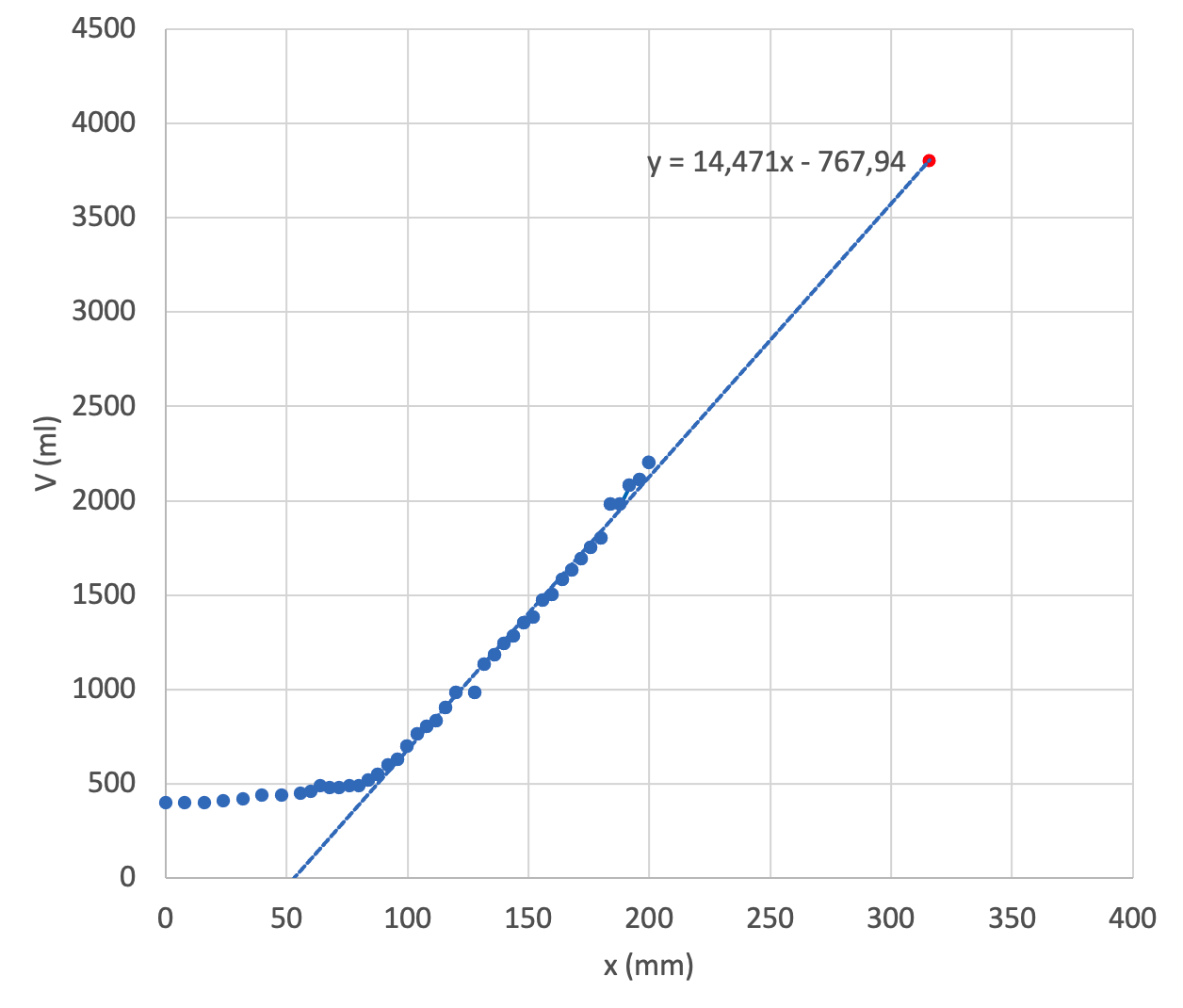
2.3 Äpplena fortsattes pressas tills veven hade vridits totalt 79 varv. Juice erhölls i samma förhållande jämfört med minskningen av volymen. Bedöm med hjälp av grafen hur mycket juice man totalt fick ur äpplena. 6 p.
Vi anpassar en rät linje till slutdelen av mätdata och avläser vid 316 mm att volymen av juicen som man får är 3,8 liter.
Alternativt får vi ekvationen V(x) = 14,5 l/m · x - 0,768 l för den räta linjen i den grafiska presentationen. Vid värdet x = 316 mm får vi svaret 3,8 liter ur ekvationen.
Poängsättning:
Det har berättats eller det syns i en graf i svaret att en extrapolering görs till värdet 316 mm eller 79 varv. (2 p.)
I lösningen har svaret givits med 2-3 gällande siffrors noggrannhet inom intervallet 3,8 L – 4,1 L och antingen syns en extrapolering i grafen eller så har den räta linjens ekvation använts för att beräkna slutresultatet. (4 p.) För övrig noggrannhet är avdrageten poäng.
Typiskt fel:
Någon annan anpassning än en rät linje har ritats i grafen, varvid slutresultatet är uppenbart fel.
3. Stöpning av nyårslyckor 15 p.
3.1 Visa att det behövs 8,2 kJ energi för att smälta sockret om man tar två matskedar (30 ml) strösocker som är vid rumstemperatur (21°C). 7 p.
Energimängden som behövs för att smälta sockret går åt till uppvärmningen och smältningen: Q = cm\Delta T + sm , där c är sockrets specifika värmekapacitet och s är sockrets specifika smältvärme.
I materialet har den molära värmekapaciteten c’ och det molära smältvärmet s’ givits. Med hjälp av dessa ska ekvationen skrivas
Q = c’ n \Delta T + s’ n.Sockrets massa är m=\rho V =30\,{\rm ml}\cdot (80\,{\rm g})/(100\,{\rm ml})=24\,{\rm g}.
Sockrets substansmängd är n = \frac{m}{M} = \frac{24\,{\rm g}}{342,3\,{\rm g/mol} } = 0,070 {\rm mol}.
Förändringen i sockrets temperatur från rumstemperatur till smältpunkten är \Delta T=462\,{\rm K} - (273,15+21)\, {\rm K}=167,85\,{\rm K}.
Energin som behövs är: Q = 0,4225\,{\rm kJ/(mol \cdot K)} \cdot 0,070 {\rm mol} \cdot 167,85\,{\rm K} + 46,2\,{\rm kJ/mol} \cdot 0,070 {\rm mol} = 8,198 {\rm kJ}.
Poängsättning:
Det har visats storhetsekvationer för energin som behövs vid uppvärmning (2 p.) och för energin som behövs vid smältning (2 p.).
Rätt svar har beräknats och det har konstaterats att det med 2–3 gällande siffrors noggrannhet är 8,2 kJ. (3 p.) För övrig noggrannhet är avdraget en poäng.
Om sockrets volym har tolkats som 60 ml i lösningen, och med hjälp av det har energibehovet beräknats till 16,4 kJ, räknas svaret som korrekt ifall att slutresultatet kommenterats på ett rationellt sätt.
3.2 Samma mängd socker som i deluppgift 3.1 smälts på en platta vars effekt är 1 200 W. Smältningen tar 2,5 minuter. Bestäm verkningsgraden för smältningen. 4 p.
Enligt deluppgift 3.1 behövs det Q=8\,212\,{\rm J} energi för att smälta sockret. Den elektriska spisens effekt är P=1\,200\,{\rm W}, alltså är energin spisen avger E=Pt. Verkningsgraden är
\eta=\frac{Q}{Pt}=\frac{8212\,{\rm J}}{1200\,{\rm W}\cdot 2,5\cdot 60\,{\rm s}}=0,046.
Verkningsgraden är alltså 4,6 %.
Poängsättning:
En korrekt löst storhetsekvation för verkningsgraden har presenterats. (2 p.)
Rätt svar har givits med 2–3 gällande siffrors noggrannhet inom intervallet 4,4 % – 4,7 % (2 p.). För övrig noggrannhet är avdraget en poäng.
3.3 Video visar parallellt uppvärmning av bly och socker vid samma förhållanden på en spis. Blystycket smälter helt och hållet efter en kort stund, men när sockerhögen smälts förblir en stor del av sockret osmält under en lång tid. Vad beror skillnaden på? 4 p.
Båda ämnen börjar smält i början av videon. Utgående från det här kan man konstatera att materialet som rör stekpannan har uppnått smältpunkten. Blystycket smälter snabbt eftersom den goda värmeledningsförmågan gör att temperaturskillnaderna i stycket är obetydliga. Sockerhögen smälter först vid kanterna och smältningen framskrider långsamt. Det här orsakas av den svaga överföringen av värme vidare från sockret som rör stekpannan. Genom att jämföra smältpunkter kan man märka att stekpannan i vilken blyet smälter är vid en högre temperatur än stekpannan med sockret. Effekten för spillvärmen som överförs från stekpannan till omgivningen är större för stekpannan med bly, alltså överförs en större värmemängd till sockret per tidsenhet.
Skillnaden beror alltså på materialens värmeledningsförmåga. Metall leder värme bättre än socker. Dessutom är värmeledning från ett föremål till ett annat, alltså från ett sockerkorn till ett annat, betydligt sämre än inuti det enhetliga metallstycket.
Poängsättning:
Det har berättats att blyets värmeledningsförmåga är större än sockrets. (2 p.)
Det har berättats att värmeöverföring i ett enhetligt stycke sker effektivare än i ett ämne som består av korn. (2 p.)
Typiskt fel:
Skillnaden har förklarats utgående från ämnenas smältpunkter, specifika värmekapaciteter eller värmekapaciteter.
4. Krafter 15 p.
4.1 En pil som flyger i luften. 4 p.
- C
- \vec{F}_4 tyngdkraft
- \vec{F}_2 luftmotstånd
4.2 En curlingsten som glider på isen efter att den skjutits iväg. 5 p.
- A
- \vec{F}_3 friktionskraft
- \vec{F}_5 isens stödkraft
- \vec{F}_6 tyngdkraft
4.3 En simboj som rör sig i vattnet, fäst med en rem vid simmarens rygg. 6 p.
- C
- \vec{F}_1 remmens spännkraft
- \vec{F}_3 vattnets motståndskraft
- \vec{F}_4 lyftkraft
- \vec{F}_5 tyngdkraft
Poängsättning:
Val av korrekt figur. (2 p.)
Varje korrekt namngivna kraftsymbol (1 p.) oberoende av vilken kraftfigur som valts.
Typiska fel:
I deluppgift 4.3 har remmens dragkraft namngetts som en kraft orsakad av simmaren.
Det har påståtts att tyngdkraften är pilens, stenens eller bojens tyngdkraft, trots att det är fråga om jordens tyngdkraft.
5. Omloppstiden för en exoplanet 15 p.
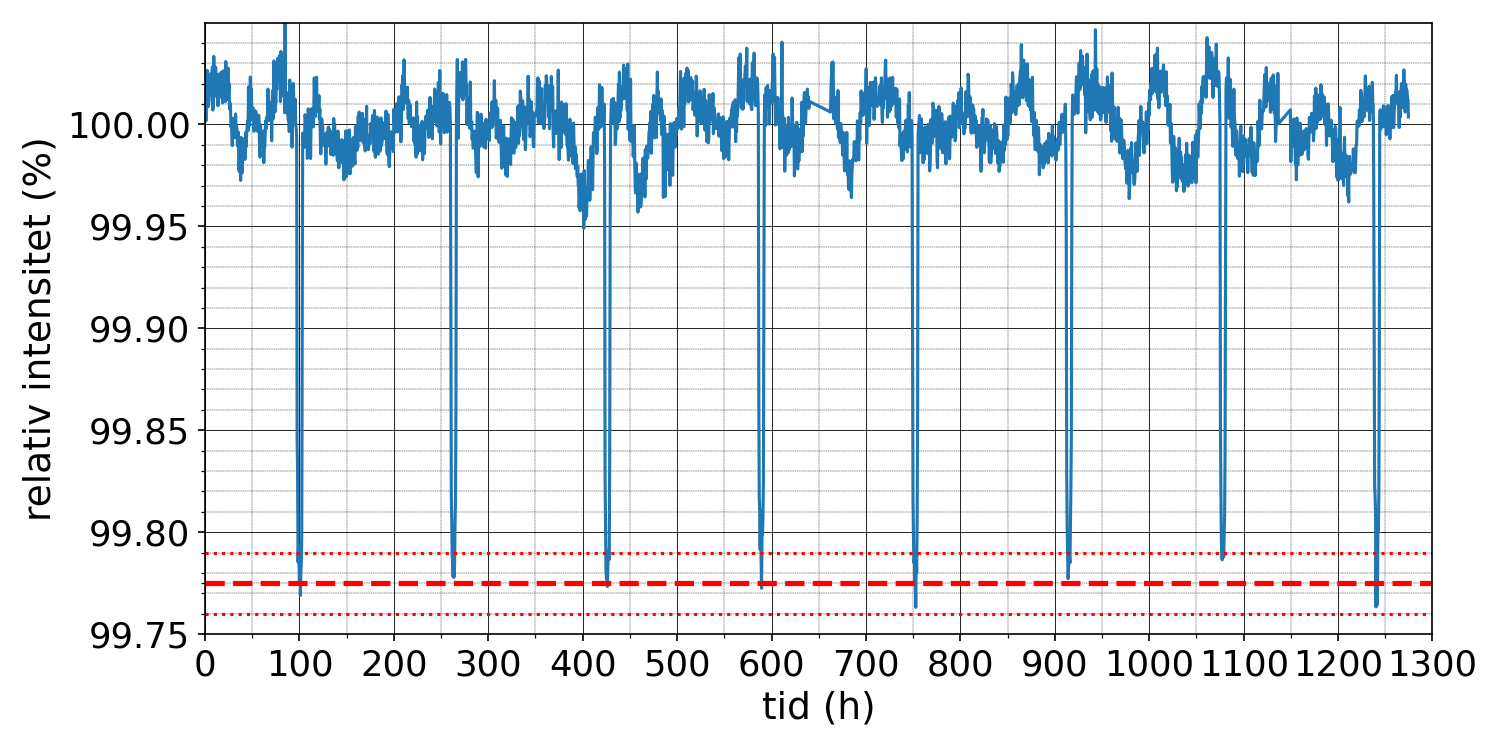
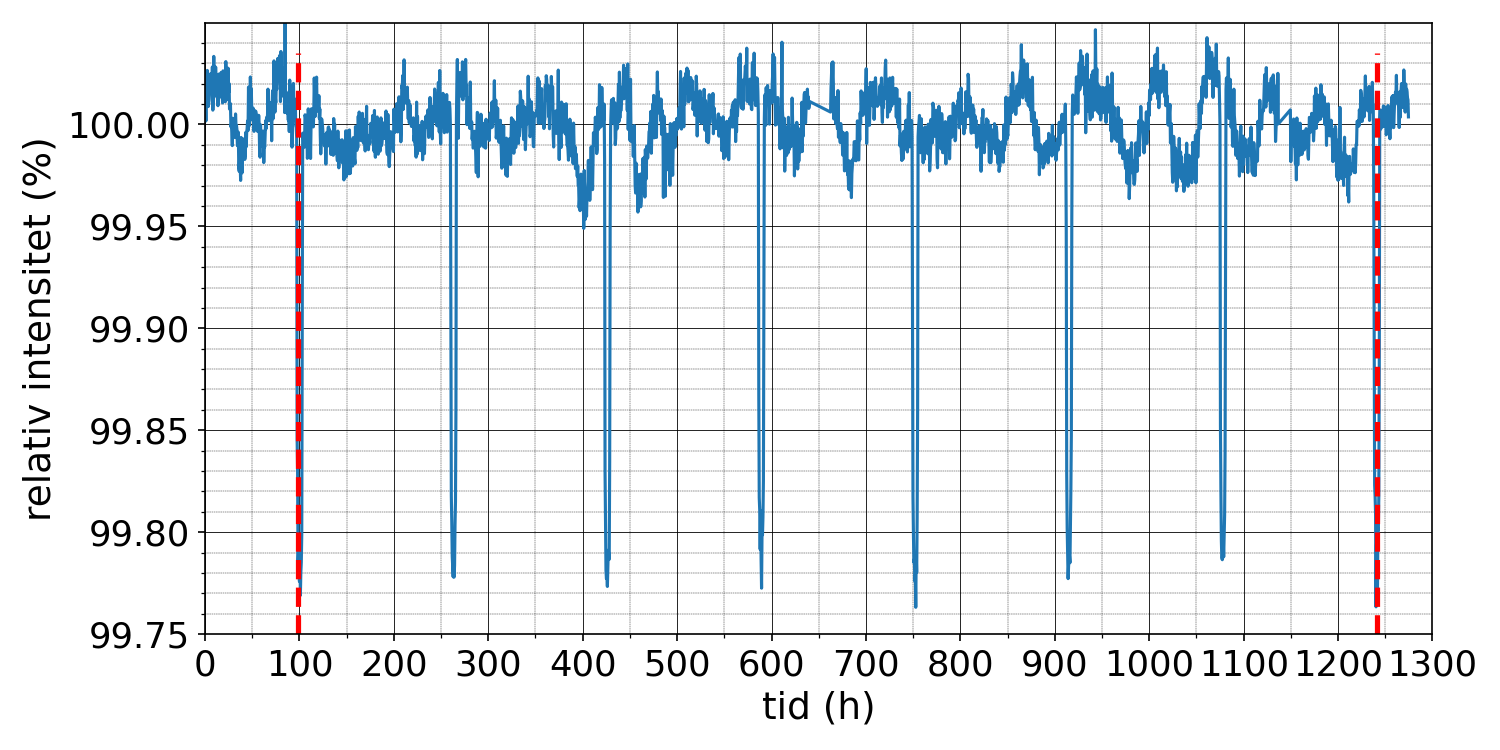
5.1 Bild visar Keplersatellitens mätningar av hur den relativa intensiteten för ljuset från en viss stjärna varierar med tiden. Hur många procent av stjärnans yta täcker planeten som mest? 3 p.
Poängsättning:
Rätt svar har givits med 2–3 gällande siffrors noggrannhet inom intervallet 0,210 % - 0,245 % (3 p.).
För övrig noggrannhet är avdraget en poäng.
5.2 Bestäm exoplanetens omloppstid runt stjärnan med hjälp av bild . 4 p.
Poängsättning:
I svaret har omloppstiden bestämts genom att använda fler än två efterföljande täckningshändelser. (2 p.)
Rätt svar har givits med 2–3 gällande siffrors noggrannhet inom intervallet 160 h – 164 h. (2 p.)
För övrig noggrannhet är avdraget en poäng.
Typiska fel:
Omloppstiden har bestämts med hjälp av endast två intilliggande täckningshändelser.
Vid beräkningen av omloppstiden har tiden för flera omlopp delats med topparnas antal i stället för intervallens antal.
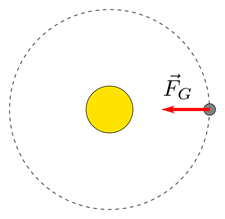
5.3 Fullborda exoplanetens kraftfigur i bild eller i någon motsvarande bild som du själv ritar. Lägg till en skärmdump i ditt svar. Exoplanetens omloppsbana är ungefär en cirkel. Beräkna cirkelbanans radie då stjärnans massa är 1,52 gånger så stor som solens massa. 8 p.
Exoplaneten som färdas i cirkelbanan påverkas endast av stjärnans gravitationskraft \vec{F}_G
Utgående från kraftfiguren är rörelseekvationen enligt Newtons II lag
\frac{GMm}{r^2}=\frac{mv^2}{r}där M är stjärnans massa, m är planetens massa, r är banans radie, G är gravitationskonstanten och v är banhastigheten.
Planetens banhastighet, uttryckt med hjälp av omloppstiden T, är v=2\pi r/T, och genom att substituerar det här i rörelseekvationen får vi för banans radie uttrycket
r=\sqrt[3]{\frac{GMT^2}{4\pi^2}}och som banans radie r = 1,21\cdot 10^{10}\,{\rm m}.
Poängsättning:
I kraftfiguren har endast en kraftvektor, namngiven som gravitationskraft, ritats från exoplaneten, och den är riktad mot moderstjärnan. (2 p.)
Ifall att kraftvektorn inte rör exoplaneten eller om andra krafter ritats fast i exoplaneten ger kraftfiguren 0 p.
En korrekt rörelseekvation för exoplaneten har presenterats. (2 p.)
En storhetsekvation som lösts korrekt för banans radie har presenterats. (2 p.)
Rätt svar för banans radie har gvits med 2-3 gällande siffrors noggrannhet inom intervallet 1,19 \cdot 10^{10} {\rm m} – 1,22 \cdot 10^{10} {\rm m}. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiska fel:
I kraftfiguren har accelerations- eller hastighetsvektorer ritats fast i exoplaneten.
Gravitationskraften som påverkar stjärnan har ritats.
6. En dammpartikel i en kondensator 15 p.
6.1 Hur stor är den elektriska fältstyrkan mellan skivorna, och vilken riktning har den? 4 p.
Poängsättning:
Rätt riktning för det elektriska fältet har presenterats. (2 p.)
Rätt svar för den elektriska fältstyrkan har givits med 2–3 gällande siffrors noggrannhet som 13,8 {\rm kV/m}. (2 p.) För övrig noggrannhet är avdraget en poäng.
6.2 Hur stor är den elektriska kraften som påverkar dammpartikeln, och vilken riktning har den? 3 p.
Poängsättning:
En storhetsekvation för kraften som påverkar partikeln har presenterats. (2 p.)
Rätt svar för kraftens storlek har givits med 2–3 gällande siffrors noggrannhet som 78,9 {\rm nN}. (1 p.) För övrig noggrannhet är avdraget en poäng.
6.3 Vi undersöker endast den elektriska kraften som påverkar partikeln. Hurdan rörelse har partikeln? Hur lång tid tar det för partikeln att färdas till kondensatorns negativt laddade skiva då partikeln startar från vila? 8 p.
Det elektriska fältet är homogent, alltså påverkas partikeln av en konstant kraft, och enligt Newtons II lag är partikelns rörelse likformigt accelererad.
Partikelns acceleration är a=F/m=QE/m=QU/(dm) och sträckan som den färdas på tiden t är d=\tfrac{1}{2}at^2. Om vi löser för tiden får vi t=\sqrt{2d/a}=\sqrt{2d^2 m/(QU)} = 0,466290575\,{\rm s} \approx 0,47\,{\rm s}.
Poängsättning:
Det har konstaterats att partikeln är i en likformigt accelererad rörelse. (2 p.)
Den likformigt accelererade rörelsen är motiverad med att kraften som påverkar partikeln är konstant. (2 p.)
En korrekt storhetsekvation för tiden har presenterats. (2 p.)
Med 2-3 gällande siffrors noggrannhet ar rätt svar för tiden givits som 0,466\,{\rm s}. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiska fel:
Det har inte nämnts att partikelns accelererade rörelse är likformigt accelererad.
I lösningen har det inte motiverats att partikeln påverkas av en konstant kraft.
7. En hoverboard 15 p.
I filmen Tillbaka till framtiden II som utkom år 1989 färdas huvudpersonen Marty McFly framåt i tiden med en tidsmaskin till år 2015. Marty använder en hoverboard för att röra sig i en framtida stad.
År 2015 presenterades en prototyp för en hoverboard som kan sväva ovanför ett koppargolv (bild ). Motorer inuti hoverboarden roterar på permanentmagneter.
7.1 Varför möjliggör hoverboardens roterande magneter att den kan sväva ovanför ett koppargolv? 6 p.
Poängsättning:
Ett föränderligt magnetiskt flöde har uppmärksammats i lösningen. (2 p.)
Det har berättats att virvelströmmar uppstå i koppargolvet. (2 p.)
Lösningen har motiverats med att växelverkan mellan det magnetiska fältet som uppstår på grund av virvelströmmarna och hoverboardens magneter är repellerande. (2 p.)
Typiska fel:
I lösningen har en elektrostatisk växelverkan behandlats istället för en magnetisk växelverkan.
7.2 Varför går det inte att sväva ovanför asfalt? 3 p.
Poängsättning:
Det har givits som motivering att virvelströmmarna inte uppstår på grund av att asfalten inte är en elektrisk ledare. (3 p.).
7.3 Vilka krafter påverkar hoverboarden i situationen i bild ? 3 p.
Poängsättning:
Varje korrekt namngivna kraft ger en poäng.
Typiskt fel:
Det har föreslagits att åkarens tyngd angriper boarden, eller så har boardens och åkarens tyngder inte särskilts.
7.4 Varför blir golvet varmt trots att hoverboarden inte rör det? 3 p.
Poängsättning:
Det har givits som motivering att virvelströmmarna orsakar uppvärmningen av golvet på grund av kopparns resistivitet. (3 p.)
Typiskt fel:
Det har påståtts att virvelströmmarna värmer golvet utan att nämna materialets resistivitet.
8. Kärnkraftverket Olkiluoto 3 15 p.
Olkiluoto 3 är ett kärnkraftverk på Finlands västkust. Det producerar elektricitet med en effekt på 1600 MW och elproduktionens verkningsgrad är 0,375. Enligt driftsplanen går kraftverket oavbrutet på full effekt 330 dygn om året. Vid ett serviceuppehåll som tar ungefär en månad görs underhåll på kraftverket och 32 ton använt bränsle byts ut mot färskt bränsle för nästa driftperiod.
Energiproduktionen i kärnkraftverket grundar sig i fissionsreaktionen av uran där urankärnan klyvs i två medeltunga kärnor. Vid varje fissionsreaktion frigörs i medeltal 0,20 GeV energi med vilket vattenånga produceras. Vattenångan roterar en turbin och turbinen roterar en generator som producerar elenergi.
8.1 Hur många fissionsreaktioner sker det per sekund i kärnkraftverket Olkiluoto 3 när det går på full effekt? 4 p.
Fissionsreaktionerna producerar värmeeffekt som kan beräknas från den kända elektriska effekten med hjälp av verkningsgraden: \eta=P_{\rm e}/ P_{\rm th}\Rightarrow P_{\rm th}= P_{\rm e}/\eta.
Antal fissioner per sekund kan man beräkna genom att dividera värmeeffekten med energimängden som frigörs vid en fissionsreaktion:
x = Pth / Efission = Pe / (η Efission) = 1600 MW / (0,375 · 0,20 GeV · 1,6021765 · 10-19 J/eV) = 1,3315 · 1020 / s ≈ 1,33 · 1020 / s.
Poängsättning:
I lösningen har det framförts en idé om att dela effekten från reaktorn med energimängden som frigörs vid en reaktion. (2 p.)
Rätt svar för fissionsreaktionernas antal har givits med 2–3 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiskt fel:
Kraftverkets verkningsgrad har inte tagits i beaktande i lösningen.
8.2 Hur mycket av bränslets massa försvinner på grund av fissionsreaktionerna under ett år, om kraftverket går enligt driftsplanen? 4 p.
Förhållandet mellan energin och massdefekten: E = mc2, ur vilket vi får m = E/c2.
Värmeenergin som produceras genom fissionsreaktionerna på ett år får vi genom att multiplicera effekten med brukstiden:
E = Pth T = Pe T / η.
Förändringen i massan under ett år är därmed:
m = Pe T / (η c2) = 1600 MW · 330 d · 24 h/d · 3600 s/h / (0,375 · (3 · 108 m/s)2) = 1,3517 kg ≈ 1,4 kg.
Poängsättning:
Sambandet mellan massdefekten och energin har behandlats korrekt i lösningen. (2 p.)
Rätt värde för massan har givits med 2-3 gällande siffrors noggrannhet som 1,35\,{\rm kg}. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiska fel:
Kraftverkets verkningsgrad har inte tagits i beaktande i lösningen.
I lösningen har det antagits att kraftverket är i bruk 365 dagar i året istället för de 330 dagar som givits i uppgiften.
8.3 Om ett kolkraftverk används för att producera samma elektriska effekt behövs en mängd stenkol som är 100 000 gånger så stor som uranbränslets massa. Vad beror den här skillnaden på? 4 p.
Vid förbränning av stenkol frigörs energi då en kolatom binds till syre, medan energi frigörs då atomkärnan klyvs vid fission av uran. Energin som frigörs vid förbränningen härrör sig från atomernas och molekylernas bindningskrafter (en elektromagnetisk växelverkan), och för varje reaktion är den i storleksordningen eV. Vid en fissionsreaktion frigörs energi på grund av nukleonernas omorganisering (en stark växelverkan) och för varje reaktion är den i storleksordningen MeV. Av uranbränslets kärnor är det typiskt endast några procent som fissioneras under användningen, men trots det behövs det 5–6 storleksordningar fler förbränningsreaktioner och kolbränsle än vad det behövs kärnreaktioner och kärnbränsle.
Poängsättning:
Det har uppmärksammats att det vid en förbränningsreaktion är fråga om den elektromagnetiska växelverkan eller frigörandet av kemisk energi och att det vid en fissionsreaktion är fråga om den starka växelverkan eller frigörandet av nukleonernas bindningsenergi. (2 p.)
Det har utgåtts från att mängden frigjord energi vid en kärnreaktion är mycket större än den frigjorda energin vid en kemisk reaktion. (2 p.)
8.4 Kolkraftverk och kärnkraftverk förorsakar under användningen skador och risker för miljön. Beskriv tre betydande skillnader mellan kolkraftverk och kärnkraftverk då det gäller skador och risker under deras brukstid. 3 p.
De mest betydande skillnaderna mellan skadorna och riskerna för kolkraftverk och kärnkraftverk under brukstiden:
- Koldioxid: Kolkraftverk producerar koldioxid vid användningen, till skillnad från kärnkraftverk.
- Luftburna partiklar: Kolkraftverk producerar luftburna partiklar vid användningen, vilket kärnkraftverk inte gör.
- Olycksrisk: I kärnkraftverk finns vid användning stora mängder radioaktiva ämnen som föranleder en risk för strålningsolyckor. Radioaktiva ämnen används inte i kolkraftverk.
Poängsättning:
För varje korrekt skillnad, där båda kraftverkstyper behandlats och deras skillnader presenterats korrekt. (1 p.)
Typiska fel:
I svaret har endast den ena kraftverkstypen behandlats utan att jämföra med en andra.
Övriga skillnader än de som gäller brukstiden har jämförts.
Del 3: 20-poängsuppgifter
9. Ett solkraftverk 20 p.
9.1 Solpanelernas energiproduktion beror på klockslaget. Den mest uppenbara orsaken till det här är att solen i augusti går upp vid 5-tiden och ner vid 22-tiden. Nämn tre andra saker som påverkar hur energiproduktionen varierar under dagens lopp. 3 p.
- Moln kastar skuggor på panelerna, och solens ljus absorberas eller sprids bort från molnen. Det här märks som snabba förändringar i produktionen.
- Vinkeln mellan solen och panelerna förändras i takt med tiden på dygnet. Positionen för maximet är inte klockan 13, alltså är panelerna riktade mot väst. Därmed träffar solens strålning panelerna bäst först på eftermiddagen.
- Träd och byggnader kastar skuggor på panelerna, alltså är de i skuggan vid olika tider på dygnet. Exempelvis klockan 14.30–15.00 finns det ett tillfälligt minimum i alla kurvor som kan vara orsakat av en sådan skugga.
- Då solen länge lyser på panelen stiger panelens temperatur och produktionen sjunker. Panelernas verkningsgrad försämras med ungefär 4 % för varje Kelvin då temperaturen stiger.
Poängsättning:
Varje rätt sak. (1 p.)
Typiskt fel:
Det har förevisats påståenden gällande energiproduktionen som inte besvarar frågan om produktionens förändringar under loppet av en dag.
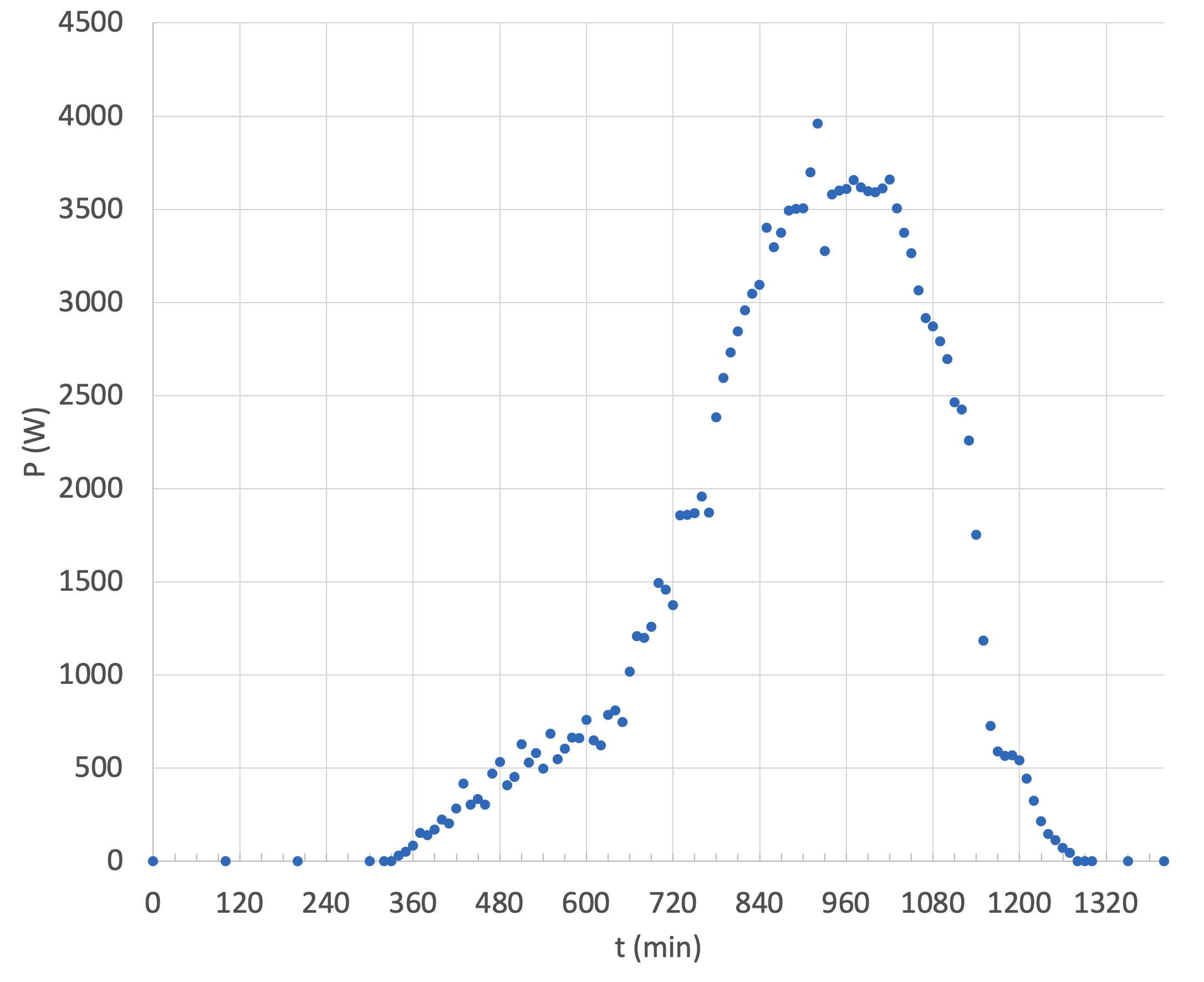
9.2 Hur mycket energi skulle det här lilla kraftverket kunna producera som mest under ett dygn i början på augusti? Gör en lämplig grafisk presentation utgående från tabell , och bestäm med hjälp av den energin som maximalt kan produceras. 9 p.
Från mätdata väljer vi den största uppmätta effekten vid varje tidpunkt och gör en egen kolumn med värdena i filen. Vi ritar en tid-effekt-graf med värdena. Det här motsvarar energiproduktionen under en molnfri dag.
Arean under grafen motsvarar energin som är producerad under ett dygn, vilken är 1550000 W·min eller 25,9 kWh eller 93,2 MJ.
Poängsättning:
I svaret framgår det att den maximala effekten för varje tidpunkt har använts. (2 p.)
Det har presenterats en graf i vilken den maximala effekten syns som funktion av tidpunkten eller tiden från midnatt. (3 p.)
I lösningen framgår det tydligt att energin erhålls från ytan under kurvan i grafen. (2 p.)
Rätt svar för energin har givits med 1–3 gällande siffrors noggrannhet inom 25 kWh – 28 kWh eller 90 MJ – 100 MJ. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiska fel:
En graf för endast en dag eller fem dagars medeltal har använts.
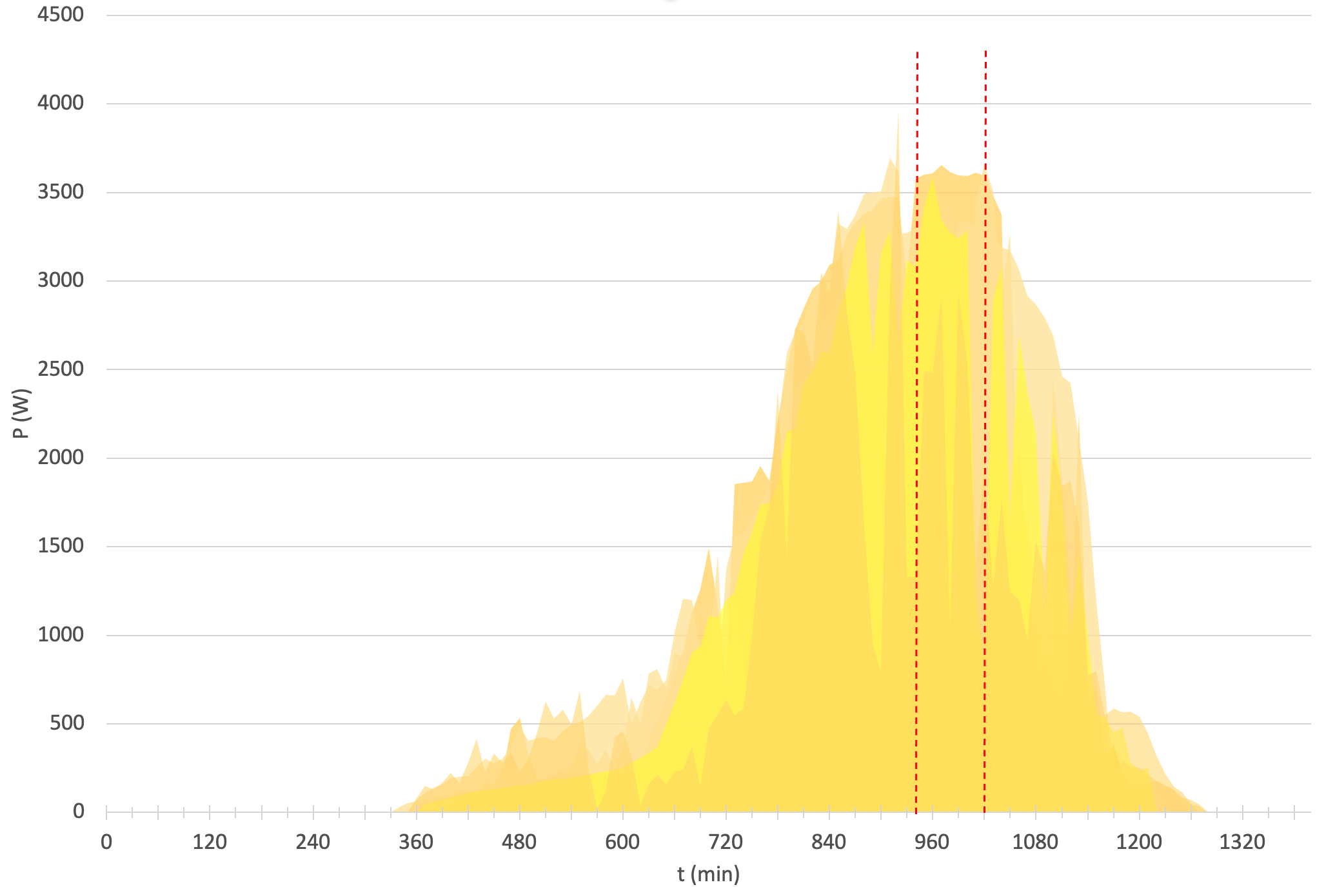
9.3 Vid vilken tid på dygnet och under en hur lång tid är panelernas energiproduktion som störst enligt idealsituationen i deluppgift 9.2? 4 p.
Vi använder den grafiska presentationen från deluppgift 9.2 eller ritar mätdata från varje dag i samma graf. Ur de här kan man dra slutsatsen att den största effekten uppnås under en 90 minuter lång period på eftermiddagen 940 minuter från midnatt, eller ungefär klockan 15.00–16.30. Grafens maximiområde är möjligtvis lite bredare än det här.
Poängsättning:
Som svar har tidpunkten för den största effekten givits inom intervallet 14.10 – 17.30. (2 p.)
Som svar har det med hjälp av den grafiska presentationen bedömts att tidsintervallets längd är inom intervallet 60 min – 200 min. (2 p.)
Typiskt fel:
Den grafiska presentationen har inte visats eller det har inte hänvisats till den på något sätt.
9.4 Enligt tillverkarens information kan solpanelerna omvandla 19 % av den strålningsenergi från solen som faller på dem till elektrisk energi. Nämn två saker som bidrar till att all strålningsenergi som faller på panelerna inte kan omvandlas till elektrisk energi. 4 p.
- En del av den inkommande strålningen reflekteras bort från panelens yta.
- Energin för strålningskvantumet måste överskrida halvledarmaterialets tröskelenergi för att panelen ska kunna producera elektricitet från strålningen. Strålning med längre våglängder än våglängden som motsvarar tröskelenergin absorberas inte av panelen så att elektricitet produceras. En betydande del (ungefär en fjärdedel) av strålningen från solen ligger i området för infraröd strålning, och energin för de här kvantumen räcker inte till för att producera elektricitet.
- Överlåtande av energi är en process mellan två partiklar. En foton som absorberas av solcellen överlåter sin energi till en elektron. Då fotonens energi är större än tröskelenergin kan cellen inte ta till vara hela fotonens energi utan endast den tröskelenergi som behövs. Därför kan all energi från strålning med kortare våglängder inte användas. En betydande del (ungefär en fjärdedel) av strålningen från solen ligger i området för ultraviolett strålning, och en betydande del av energin från de här kvantumen blir överlopps.
Poängsättning:
Reflektion (2 p.) har identifierats i lösning, eller det har berättats att det krävs en minimienergi för kvantumet (2 p.), eller det har berättats att en del av kvantumets energi går till spillo (2 p.), men endast så att de totala poängen för ett svar inte överskrider fyra poäng.
Typiskt fel:
Det har påståtts att energin reflekteras.
10. En bilbana 20 p.
10.1 Bilen färdas upp och nedvänd i bilbanans högsta punkt men hålls ändå på banan. Vad är dess lägsta möjliga hastighet vid den här punkten? 6 p.
Enligt Newtons II lag gäller för krafterna i y-riktningen vid banans högsta punkt att G-N = ma_{\rm n}, där bilens normalacceleration a_{\rm n} är mot mittpunkten för den största loopen. Hastigheten är som minst vid gränsfallet där N = 0 varvid G = m a_{\rm n}.
Normalaccelerationen är a_{\rm n} = v^2/r och bilens tyngd är G = mg. Alltså blir mg = m v^2/r, ur vilket vi får bilens lägsta möjliga hastighet: v=\sqrt{gr}=\sqrt{9,81\,\frac{\rm m}{{\rm s}^2}\cdot \frac{0,51}{2}\,{\rm m}}=1,581629\,{\rm m/s} \approx 1,6\,{\rm m/s}.
Poängsättning:
I lösningen har det omnämnts att normalkraften försvinner vid gränsfallet (2 p.),
bilens rörelseekvation har skrivits med storhetssymboler (2 p.) och rätt svar har givits med 2–3 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiskt fel:
Det har inte berättats att normalkraften är noll vid gränsfallet.
10.2 Bilen skjuts iväg på banan med hastigheten 3,1 m/s. Efter att ha kört genom banan flyger bilen från rampen till en höjd på 32 cm och landar sedan på banans nivå vid ett avstånd av 15 cm från flygbanans högsta punkt (bild ). Du kan anta att motståndskrafterna som påverkar bilen under flygturen är obetydliga, alltså hålls den vågräta komponenten av bilens hastighet konstant under flygturen, medan den lodräta komponenten ändrar likformigt. Hur stort arbete utförde motståndskrafterna som påverkade bilen under hela banans sträcka? 7 p.
Enligt mekanikens energiprincip är E_{p1}+ E_{k1}+W= E_{p2}+ E_{k2}, där W är arbetet som motståndskrafterna utför. Bilens mekaniska energi är i början E_{p1}=0 och E_{k1}=\tfrac{1}{2}mv_0^2 och i slutet E_{p2}=mgh och E_{k2}=\tfrac{1}{2}mv^2, alltså får vi ur energiprincipen ekvationen \tfrac{1}{2}mv_0^2-W = mgh+\tfrac{1}{2}mv^2, varvid W=m(\tfrac{1}{2}v_0^2-gh-\tfrac{1}{2}v^2).
Bilens hastighet under hoppet kan beräknas med hjälp av bilens fallrörelse. Bilen faller den lodräta sträckan h samtidigt som den färdas den vågräta sträckan x. I den högsta punkten är hastigheten i y-riktningen noll, varvid h=\tfrac{1}{2}gt^2, ur vilket vi får tiden som det tar för bilen att falla t=\sqrt{2h/g}. Från den högsta punkten färdas bilen den vågräta sträckan x=vt, vilket ger oss bilens hastighet v = x/\sqrt{2h/g} = 0,15\,{\rm m}/\sqrt{2\cdot 0,32\,{\rm m}/(9,81\,{\rm m/s}^2)} = 0,587267\,{\rm m/s}. Arbetet som motståndskrafterna utför är då: W=m(\tfrac{1}{2}v_0^2-gh-\tfrac{1}{2}v^2) = 0,037\,{\rm kg}\cdot \Bigl( \tfrac{1}{2}\cdot\bigl( 3,1\,\tfrac{\rm m}{\rm s}\bigr)^2 -9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot 0,32\,{\rm m} -\tfrac{1}{2}\cdot \bigl( 0,587267\,\tfrac{\rm m}{\rm s}\bigr)^2\Bigr) = 0,0552543\,{\rm J} \approx 0,055\,{\rm J}.
Poängsättning:
Lösningen har med ord motiverats genom mekanikens energiprincip. (1 p.)
Rätt storhetsekvation har skrivits för bilens hastighet antingen vid hoppets krön eller vid hoppets slut, eller hastigheten i fråga har lösts korrekt. (2 p.)
Rätt storhetsekvation har skrivits för arbetet som motståndskrafterna utför (2 p.) och rätt svar har givits som antingen positivt eller negativt med 1–3 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiskt fel:
Bilens rörelseenergi vid krönet har glömts.
10.3 Olika leksaksbilar fungerar på lite olika sätt på banan. Vi väljer en leksaksbil vars begynnelsehastighet och motståndskrafter är sådana att bilen passerar de högsta punkterna på den första och den andra loopen med de lägsta möjliga hastigheterna. Kan bilen då även passera genom den tredje loopen? Du kan anta att motståndskrafterna som påverkar bilen i medeltal är lika stora i alla av banans loopar. 7 p.
Stödkraften mellan banan och bilen är noll om bilen rör sig med den lägsta möjliga hastigheten. Då gäller samma villkor för krafterna i y-riktningen i de högsta punkterna på de två första looparna som användes i deluppgift 10.1, alltså G=ma_n. Från det här får vi v_n=\sqrt{gr_n}.
Den totala mekaniska energin i looparnas högsta punkter är då:
- vid första loopen: mgd_1+\tfrac{1}{2}mv_1^2=mgd_1+\tfrac{1}{2}mgr_1=E_1,
- vid andra loopen: mgd_2+\tfrac{1}{2}mv_2^2=mgd_2+\tfrac{1}{2}mgr_2=E_2.
Bilens totala mekaniska energi i den högsta punkten på första loopen är E_1=mgd_1+\tfrac{1}{2}mgr_1=0,037\,{\rm kg}\cdot 9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot (0,51\,{\rm m}+\tfrac{1}{2}\cdot \tfrac{0,51\,{\rm m}}{2}) = 0,23139338\,{\rm J}.
I den andra loopens högsta punkt har den totala energin minskat med en mängd som motsvarar arbetet som motståndskrafterna utför, W=-F\Delta x_1, varvid E_2=mgd_2+\tfrac{1}{2}mgr_2=E_1-F\Delta x_1, där avståndet längs med banan mellan de högsta punkterna på första och andra loopen är \Delta x_1 = \tfrac{1}{2}2\pi r_1+\tfrac{1}{2}2\pi r_2=\tfrac{1}{2}\pi(d_1+d_2) = \tfrac{1}{2}\pi(0,51\,{\rm m}+0,38\,{\rm m})=1,3980087\,{\rm m}.
Vi får den genomsnittliga motståndskraften F=\frac{1}{\Delta x_1}(E_1-mgd_2-\tfrac{1}{2}mgr_2)=0,042190455\,{\rm N}.
Vid den tredje loopen har energin ytterligare minskat med arbetet som motståndskrafterna utför på sträckan \Delta x_2, alltså är den totala energin i den högsta punkten på tredje loopen E_3=E_1-F\Delta x_1-F\Delta x_2=E_1-F(\Delta x_1+\Delta x_2), där avståndet längs med banan mellan de högsta punkterna på andra och tredje loopen är \Delta x_2=\tfrac{1}{2}2\pi r_2+\tfrac{1}{2}2\pi r_3=\tfrac{1}{2}\pi(d_2+d_3) = \tfrac{1}{2}\pi(0,38\,{\rm m}+0,25\,{\rm m})=0,98960169\,{\rm m}.
Den totala mekaniska energin är då E_3=E_1-F(\Delta x_1+\Delta x_2)=0,13065900\,{\rm J}.
Leksaksbilen kommer att passera även den tredje loopen om dess hastighet vid den högsta punkten är högre än den lägsta möjliga hastigheten, alltså v_n=\sqrt{gr_n}. Då måste den totala mekaniska energin som minst vara E_{\rm min}=mgd_3+\tfrac{1}{2}mgr_3=0,037\,{\rm kg}\cdot 9,81\,\tfrac{\rm m}{{\rm s}^2}\cdot \bigl(0,25\,{\rm m}+\tfrac{1}{2}\cdot \tfrac{0,25\,{\rm m}}{2}\bigr)=0,11342813\,{\rm J}.
I det fallet är energin större än den minsta möjliga energin, alltså E_3 > E_{\rm min}, och därmed passerar leksaksbilen även den tredje loopen.
Poängsättning:
Det har uttryckts att skillnaden mellan de mekaniska energierna (E_{\rm 1}) ja (E_{\rm 2}) i de högsta punkterna i looparna 1 och 2 behövs. (1 p.)
De korrekta storhetsekvationerna har skrivits för energierna E_{\rm 1} och E_{\rm 2} eller deras korrekta värden har beräknats. (1 p.)
En korrekt storhetsekvation för den genomsnittliga motståndskraften har skrivits eller dess värde har beräknats rätt. (2 p.)
En korrekt storhetsekvation har skrivits för den mekaniska energin E_{\rm 3} eller för den motsvarande hastigheten vid högsta punkten i den tredje loopen. (1 p.)
Det har givits ett korrekt motiverat svar om att bilen passerar den tredje. (2 p.)
Typiska fel:
Bilens rörelseenergi eller potentiell energi vid loopens högsta punkt har glömts.
Det har antagits att arbetet som motståndskrafterna utför är lika stort i varje loop.
11. Röntgendiffraktion och elektrondiffraktion 20 p.
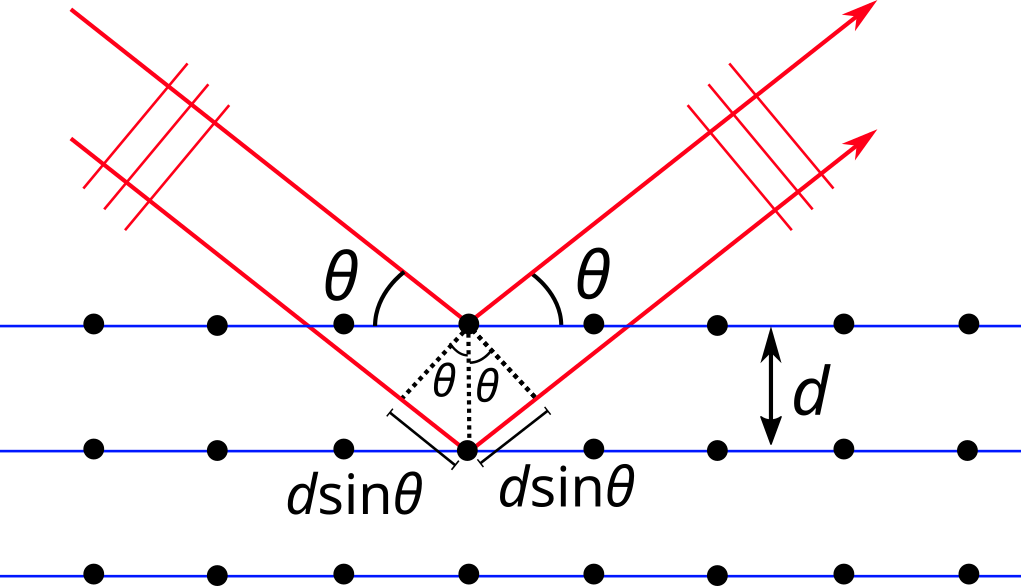
11.1 Använd bilden i material för att härleda Braggs lag 2d sin θ = nλ, där θ är vinkeln mellan strålningen och atomplanen, λ är strålningens våglängd och n är ordningstalet för diffraktionen. 5 p.
Vi undersöker strålar som har spridits från två plan som ligger ovanpå varandra. En stråle som sprids från det nedre planet har färdats en längre sträcka än en stråle som sprids från det övre planet. Skillnaden i sträckorna som strålarna färdats, vägskillnaden, kan observeras i bilden då vågfronter läggs till på lämpliga ställen. Från de två rätvinkliga trianglarna kan vi avläsa vägskillnaden som 2d sin θ. För att strålarna (egentligen vågfronterna) ska vara i samma fas när de träffar detektorn måste vägskillnaden vara en multipel av våglängden, alltså kräver vi att 2d sin θ = nλ, vilket är Braggs lag.
Poängsättning:
Med hjälp av bilden har vägskillnaden mellan strålarnas förklarats korrekt. (3 p.)
Utgående från konstruktiv interferens har det motiverats att vägskillnaden ska vara en multipel av våglängden. (2 p.)
Typiskt fel:
En hänvisning till bilden har inte gjorts, eller vägskillnaden har beräknats fel utgående från den.
11.2 Bild visar en röntgendiffraktionsgraf uppmätt från järn, där tre intensitetsmaximum av första ordningen (n = 1) syns. Mätningen gjordes med strålning vars våglängd var λ = 0,15406 nm. Vilket av intensitetsmaximumen (a, b, c) motsvarar det minsta avståndet mellan atomplanen? Bestäm avståndet. 5 p.
Från Braggs lag ser vi att ju större diffraktionsvinkel, desto mindre är värdet på d. Det minsta avståndet mellan atomplanen motsvaras av intensitetsmaximum c. Ur spektrumet i bild 11.B avläser vi vinkeln θ för pik c: θ = 41,0º. Vi omskriver Braggs lag i formen d = λ / (2 sin θ), då n = 1. Genom att substituera för vinkeln och våglängdens värde λ = 0,15406 nm får vi som avstånd mellan planen d = 0,117 nm.
Poängsättning:
Maximum c har valts med motiveringar. (3 p.)
Rätt svar har givits med 2–3 gällande siffrors noggrannhet (2 p.) genom att använda en vinkel mellan 40,5˚ – 41,5˚. För övrig noggrannhet är avdraget en poäng.
11.3 I ett visst röntgendiffraktionsexperiment användes den så kallade Kα-röntgenstrålningen från molybden, vars energi är 17,48 keV. I ett annat diffraktionsexperiment användes elektroner i stället för röntgenstrålning. Bestäm elektronernas hastighet som procent av ljusets hastighet då elektronernas de Broglie-våglängd är lika stor som röntgenstrålningens våglängd. 6 p.
Vi bildar ett uttryck för Kα-strålningens våglängd. Det är fråga om en foton, alltså är E = hf = hc/λ. Ur det här får vi λ = hc/E.
För de Broglie-våglängden gäller λ = h/p, där p = mv är elektronens rörelsemängd. Vi kräver att våglängderna ska vara lika, alltså är hc/E = h/(mv). Vi löser för hastigheten v = E/(mc).
Svaret begärdes som en bråkdel av c, alltså v/c = E/(mc²). Om vi använder elektronens viloenergi, alltså 511 keV, får vi v/c = 17,48 keV / 511 keV = 0,03421, alltså 3,4 % av ljusets hastighet.
Eller: v/c = (17,48 · 103 · 1,6022 · 10-19 J) / (9,109 · 10-31 kg (2,998 · 108 m/s)2) = 0,03421, alltså är hastigheten 3,4 % av ljusets hastighet.
Poängsättning:
En korrekt storhetsekvation eller korrekt värde har givits för den elektromagnetiska strålningens våglängd. (2 p.)
Korrekt storhetsekvation har lösts för v eller förhållandet v/c. (2 p.)
Rätt svar har givits med 2–5 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget en poäng.
Typiskt fel:
Den elektromagnetiska strålningens våglängd har förväxlats med elektronens våglängd.
11.4 Hur stor accelerationsspänning behövs för att accelerera elektronerna till hastigheten som efterfrågades i deluppgift 11.3? 4 p.
Elektronernas hastighet är ungefär 3 % av ljusets hastighet, alltså är det inte nödvändigt att beakta relativitetsteorin. Den kinetiska energin är Ek = mv²/2. Elektronerna accelereras över spänningen U, varvid de får energin Ek = eU, där e är elementarladdningen. Från det här får vi eU = mv²/2, och vidare
U=\tfrac{mv^2}{2e}=\tfrac{E_k^2}{2emc^2}\approx 298,9\,{\rm V}.
Poängsättning:
Korrekt storhetsekvation för accelerationsspänningen har givits. (2 p.)
Rätt svar har givits med 1–5 gällande siffrors noggrannhet. (2 p.) För övrig noggrannhet är avdraget en poäng.