Hyvän vastauksen piirteet: FI – Fysiikka
24.9.2024
Lopulliset hyvän vastauksen piirteet 14.11.2024
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
Yleisinä pisteytyksen linjauksina ovat:
- Jos vastauksessa annettujen merkitsevien numeroiden määrä poikkeaa HVP:ssa kirjatusta, vähennetään jokaisen vastauksen kohdalla yksi piste.
- Jos lopputuloksen yksikkö on väärin tai puuttuu, tulos on väärin.
Osa 1: 20 pisteen tehtävä
1. Monivalintatehtäviä fysiikan eri osa-alueilta 20 p.
Valitse jokaisessa osatehtävässä parhaiten soveltuva vaihtoehto. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
1.1 Kun jääpala sulaa vesilasissa, 2 p.
- veden pinnan korkeus ei muutu. (2 p.)
1.2 Jäätiköiden sulamisesta puhutaan paljon. Kun jäätikkö sulaa, 2 p.
- se sitoo lämpöä ilmakehästä ja laskee ympärillään olevan ilman lämpötilaa. (2 p.)
1.3 Kun kitaran kieli värähtelee, 2 p.
- kielen molemmissa päissä on solmu. (2 p.)
1.4 Päistään kiinnitetty kitaran kieli värähtelee vapaana ja siitä syntyy ilmassa etenevä aalto. Kun kitaran kielen värähtelytaajuus kasvatetaan kaksinkertaiseksi, 2 p.
- äänen nopeus ilmassa ei muutu. (2 p.)
1.5 Kun pariston napoihin on kytketty vastus, vastuksessa 2 p.
- sähkövirran suunta ja elektronien kulkusuunta ovat vastakkaiset siten, että elektronit kulkevat pariston negatiiviselta navalta positiiviselle navalle. (2 p.)
1.6 Kun 1,5 kΩ:n vastus on kytketty 1,5 V:n pariston napojen väliin, vastuksen napojen välinen jännite on 1,5 V. Pidetään ensimmäinen vastus paikallaan ja kytketään saman pariston napojen väliin lisäksi kaksi keskenään sarjaan kytkettyä 1,5 kΩ:n vastusta. Tällöin ensimmäisen vastuksen napojen välinen jännite on 2 p.
- 3,0 V. (2 p.)
- 0,75 V. (2 p.)
- 0,375 V. (2 p.)
- 1,5 V. (2 p.)
1.7 Valitse oikea vaihtoehto. 2 p.
- Kitkavoima on vektorisuure ja kitkakerroin on skalaarisuure. (2 p.)
1.8 Valitse oikea vaihtoehto. 2 p.
- Liike-energia on skalaarisuure ja liikemäärä on vektorisuure. (2 p.)
1.9 Atomiytimen alfahajoamisessa ydin emittoi 2 p.
- heliumytimen. (2 p.)
1.10 Parinmuodostuksessa 2 p.
- fotoni vuorovaikuttaa atomiytimen kanssa ja syntyy elektroni ja positroni. (2 p.)
Osa 2: 15 pisteen tehtävät
2. Aitajuoksu 15 p.
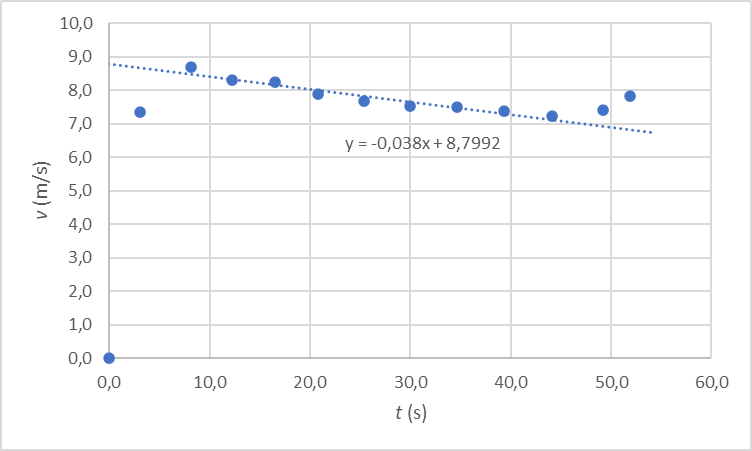
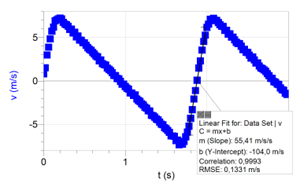
2.1 Laadi graafinen esitys McLaughlinin vauhdista ajan funktiona. Juoksun keskivaiheilla vauhdin voidaan havaita muuttuvan tasaisesti. Määritä kiihtyvyyden suuruus aikavälillä 8,0 s – 45 s. 7 p.
Lineaarinen sovite kysytylle alueelle antaa McLauglinille kiihtyvyyden a = −0,03796 m/s2 ≈ −0,038 m/s2. McLaughlinin vauhti siis hidastui noin 0,038 m/s2 matkan keskivaiheilla.
Pisteytys:
On esitetty kuvaaja, jossa mitatut McLaughlinin vauhdin arvot ajan funktiona näkyvät erillisinä mittauspisteinä. (3 p.)
-
Jos mittauspisteet eivät näy tai niitä puuttuu, vähennetään kaksi pistettä.
-
Jos akselin lukuarvot ovat väärin tai puuttuvat, vähennetään kaksi pistettä.
-
Jos kuvaajassa näkyy kaksi erilaista sovitetta tai sovite ja murtoviiva, vähennetään yksi piste.
-
Jos suureen tunnus puuttuu tai suureen yksikkö puuttuu tai akselit ovat väärin päin, vähennetään kustakin virheestä yksi piste.
On esitetty lineaarinen sovite graafisessa esityksessä ja käytetty sen antamaa kulmakerrointa. (2p.)
On annettu vastauksena 2 – 3 merkitsevän numeron tarkkuudella kiihtyvyys, jonka itseisarvo on välillä 0,037 \rm m/s^2 - 0,039 \rm m/s^2. (2 p.)
Tyypillisiä virheitä:
-
Kuvaajana on annettu pelkkä murtoviiva, jolloin yksittäiset mittauspisteet eivät erotu.
-
Määritetty keskikiihtyvyys kahden \left(v{,}t\right) -pisteen avulla.
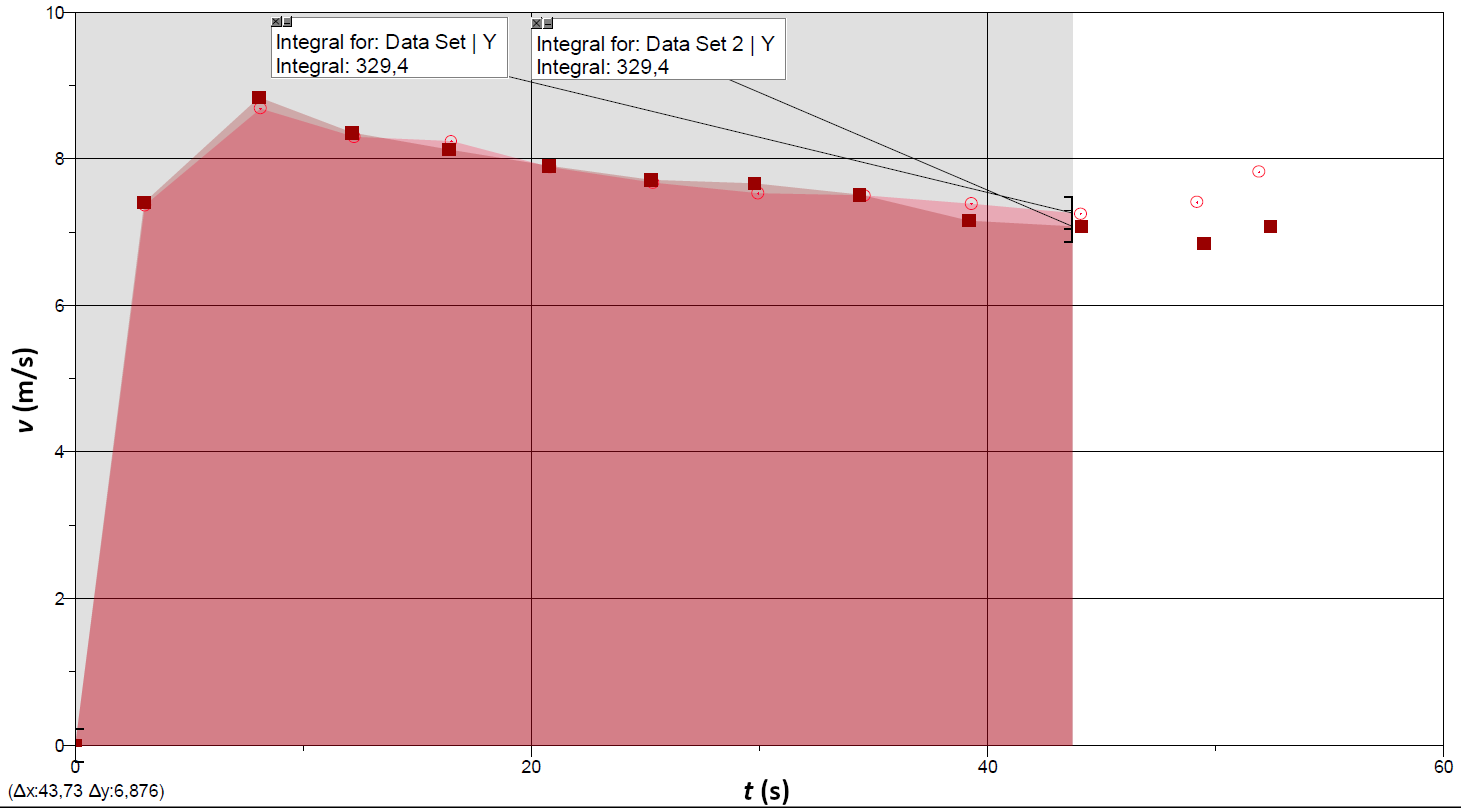
2.2 Juoksun keskivaiheilla McLaughlin pystyi kirimään Muhammadin etumatkan kiinni. Määritä graafisen esityksen avulla molempien juoksema matka aikavälillä 0–26 s. Kumpi johti kilpailua, kun matkaa oli juostu 26 sekuntia? 5 p.
Graafisella tai numeerisella integroinnilla on mahdollista määrittää molempien juoksijoiden kulkema matka tietyllä ajan hetkellä. Muhammadin kunkin ajan hetken vauhti lisätään samaan kuvaan McLaughlinin vastaavan vauhdin kanssa, jolloin saadaan seuraava kuva ja integraalit:
Integraaleista nähdään, että McLaughlin oli 26 sekunnissa juossut matkan 197,3 m, kun taas Muhammad oli samassa ajassa juossut 198,1 m.
Näin ollen Muhammadin johto oli x = 198,1 m – 197,3 m = 0,8 m, kun matkasta oli juostu 26 s.
Pisteytys:
On esitetty kuvaaja ja kerrottu siinä käyrän alle jäävän pinta-alan kuvaavan juostua matkaa. (2 p.)
On annettu vastauksena 3 – 4 merkitsevän numeron tarkkuudella oikealla periaatteella lasketut molempien kulkemat matkat. Matkojen tulee olla noin 200 m ja Muhammadin kulkeman matkan tulee olla hiukan suurempi. (2 p.)
On vastattu, että Muhammad johtaa. (1 p.)
Tyypillisiä virheitä: On laskettu kuljettu matka kertomalla nopeus ja aikasarakkeet keskenään ikäänkuin nopeus olisi vakio.
2.3 Kuinka pitkän juoksumatkan jälkeen McLaughlin ohitti Muhammadin? 3 p.
Graafisella tai numeerisella integroinnilla on mahdollista verrata molempien juoksijoiden samassa ajassa juoksemia matkoja myöhempinäkin ajankohtina.
Vertailemalla molempien käyrien alla olevia pinta-aloja huomataan, että molemmat kilpailijat olivat juosseet samassa ajassa yhtä pitkän matkan, kun noin 329 metriä kokonaismatkasta oli takana. (3 p.) Aikaisemmissa ajankohdissa Muhammad oli juossut pidemmän matkan, kun taas myöhemmissä ajankohdissa McLaughlin oli selvässä johdossa. Näin ollen McLaughlin ohitti Muhammadin, kun matkasta oli juostu x = 329 m.
Pisteytys: On annettu graafisen tai numeerisen integroinnin avulla laskettu oikea matka 2 – 4 merkitsevän numeron tarkkuudella välillä 320 \rm{m} - 340 \rm{m} (3 p).
Tyypillisiä virheitä:
-
On laskettu kuljettu matka kertomalla nopeus ja aikasarakkeet keskenään ikäänkuin nopeus olisi vakio.
-
On vastattu ohittamisen ajanhetki matkan sijaan.
3. Ilmalämpöpumppu 15 p.
Taloa jäähdytetään kuumana kesäpäivänä ilmalämpöpumpulla, joka siirtää lämpöä talon sisältä ulkoilmaan. Jäähdytyksen ansiosta talon sisälämpötila on 21 ˚C, kun ulkoilman lämpötila on 25 ˚C. Taloa jäähdyttävän ilmalämpöpumpun suorituskyky on 3,2. Lämpöpumppu kuluttaa tunnin aikana 1,6 kWh sähköenergiaa.
Ilmalämpöpumpussa on sisäyksikkö ja ulkoyksikkö. Talon ulkoseinään kiinnitetty ulkoyksikkö tekee työn lämmön siirtämiseen sisältä ulos. Ilmalämpöpumpun energiavirrat on esitetty kuvassa . Ilmalämpöpumpun suorituskyky jäähdytyksessä on talosta lämpönä pois siirretyn energian suhde pumpun tarvitsemaan sähköenergiaan.
3.1 Kuinka paljon lämpöä (yksikkönä kWh) siirtyy pois talosta tunnissa? 5 p.
Suorituskyky \varepsilon on määritelmän mukaan talosta pois siirtyneen lämmön suhde lämpöpumpun tekemään työhön
\varepsilon=\frac{Q_0}{W},
joten Q_0=\varepsilon W = 3{,}2 \cdot 1{,}6 \rm{ kWh} = 5,12 kWh ≈ 5,1 kWh.
Pisteytys:
On esitetty lämmölle ratkaistu oikea suureyhtälö. (2 p.)
On annettu itseisarvoltaan oikea vastaus 2 – 3 merkitsevän numeron tarkkuudella. (3 p.)
Tyypillisiä virheitä:
-
Ratkaistu suureyhtälö puuttuu.
-
Ei ole käytetty hyväksi annettua kuvaa ilmalämpöpumpun energiavirtakaaviosta.
3.2 Kuinka paljon lämpöä (yksikkönä kWh) siirtyy ulkoilmaan tunnissa? 5 p.
Lämpöopin ensimmäisen pääsäännön mukaan talosta ulkoilmaan siirtynyt lämpö on
Q_1=W+Q_0,
joten Q_1 = W + \varepsilon W = 1,6 kWh + 5,12 kWh = 6,72 kWh ≈ 6,7 kWh.
Pisteytys:
On perusteltu ulkoilmaan siirtyneen lämmön määrä lämpöopin ensimmäisen pääsäännön, energian säilymisen tai aineiston kuvan avulla. ( 2p.)
On esitetty lämmölle ratkaistu oikea suureyhtälö. (2 p.)
On annettu itseisarvoltaan oikea vastaus 2 – 3 merkitsevän numeron tarkkuudella. (1 p.)
Tyypillisiä virheitä:
-
Ei ole tunnistettu eroa talosta pois siirtyvän ja ulkoilmaan siirtyvän lämmön välillä.
-
Annettu vastauksena 3,5 kWh.
3.3 Ulkoilman lämpötila nousee 32 ˚C:een. Kuinka suuri lämpöpumpun sähkötehon tulee olla, jos talon sisälämpötilana halutaan edelleen pitää 21 ˚C? Voit olettaa, että lämpöpumpun suorituskyky ei riipu lämpötilasta. Voit olettaa myös, että lämpöä siirtyy taloon ulkoilmasta vain johtumalla ja johtumisen teho on verrannollinen lämpötilaeroon. 5 p.
Jotta talon sisälämpötila ei muuttuisi, tulee pumpun siirtää lämpöä talosta yhtä suurella teholla kuin sitä johtuu ulkoa sisään. Lämmönjohtumisen teho talon ja ulkoilman välillä on suoraan verrannollinen lämpötilaeroon P=UA\Delta T , missä U on lämmönläpäisykerroin ja A johtumisen pinta-ala. Kun lämpötilaero \Delta T kasvaa 4 ⁰C:sta 11 ⁰C:een, tarve siirtää lämpöä pois talosta kasvaa lämpötilaerojen suhteessa. Tähän tarvittava sähköteho kasvaa samassa suhteessa eli
P_{\rm uusi}=P\frac{\Delta T_{\rm uusi}}{\Delta T}=1,6\,{\rm kW}\,\frac{11\, ^\circ{\rm C}}{4\, ^\circ{\rm C}}=4,4\,{\rm kW}.
Pisteytys:
On esitetty kysytylle teholle tai tunnissa tehtävällä työlle ratkaistu suureyhtälö, josta näkyy oikea riippuvuus lämpötilaeroista. (2 p.)
On annettu itseisarvoltaan oikea vastaus teholle 2 – 3 merkitsevän numeron tarkkuudella. (3 p.)
Tyypillisiä virheitä: On ratkaistu tehtävä ilman suureyhtälöitä.
4. Maanvyöry 15 p.
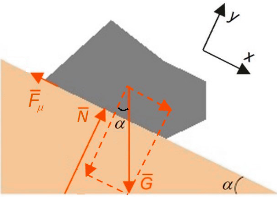
4.1 Määritä lohkareen kiihtyvyys. 8 p.
Lohkareen massa on m=2200\,{\rm kg} ja kallionrinteen kaltevuuskulma \alpha=28^\circ. Lohkareen kiihtyvyys on a. Lohkareeseen vaikuttavat painovoima \bar G, pinnan tukivoima \bar N ja kitkavoima \bar F_\mu. Kirjoitetaan Newtonin II laki komponenttimuodossa:
x-suunta:
ma=G\sin\alpha-F_\mu
y-suunta:
N-G\cos\alpha=0.
Painovoima on G=mg, jossa g=9,81\,{\rm m/s}^2 on putoamiskiihtyvyys. Liukukitkaa kuvataan yksinkertaisella kitkakerroinmallilla, F_\mu=\mu N, jossa \mu=0,40 on lohkareen ja kalliorinteen välinen liukukitkakerroin. Koska y-suunnan liikeyhtälön mukaan N=G\cos\alpha=mg\cos\alpha, saadaan kitkavoimaksi F_\mu=\mu mg\cos\alpha. Nyt x-suunnan liikeyhtälöstä voidaan määrittää lohkareen kiihtyvyys:
a=g(\sin\alpha-\mu\cos\alpha)=1,141\,{\rm m/s}^2\approx 1,1\,{\rm m/s}^2.
Pisteytys:
On esitetty lohkareen voimakuvio, jossa näkyy vain kolme oikeaan suuntaan olevaa, nimettyä voimanuolta. (2 p.)
-
Pieni ilmanvastusta oikein kuvaava nuoli sallitaan.
-
Jos voimanuoli on irti lohkareesta tai lohkareeseen on piirretty kiinni muita nuolia, voimakuviosta annetaan 0 p.
-
Jos voimien nimeäminen puuttuu tai ei ole yksikäsitteinen, voimakuviosta annetaan 0 p.
On esitetty lohkareelle oikea rinteen suuntainen liikeyhtälö muodossa ma=G_{\rm x} \ldots, ma = G \sin{\alpha} \ldots tai ma = mg \sin{\alpha} \ldots (2 p.)
On esitetty lohkareelle oikea liikeyhtälö tai tasapainoyhtälö rinnettä vastaan kohtisuorassa suunnassa. (2 p.)
Liikeyhtälöt voi kirjoittaa myös vektoreiden avulla.
On annettu kiihtyvyyden suhteen ratkaistu oikea suureyhtälö ja oikea kiihtyvyyden arvo 2 – 3 merkitsevän numeron tarkkuudella. (2 p.)
Tyypillisiä virheitä:
-
Piirretään nopeutta tai kiihtyvyyttä kuvaava voimanuoli kiinni kappaleeseen.
-
Käytetään väärää trigonometristä funktiota jaettaessa voimia komponentteihin.
-
Kirjoitetaan liikeyhtälö vektoreiden avulla väärin, esimerkiksi m \vec{a} = \vec{G}_{\rm x} - \vec{F}_{\mu} tai ma = \vec{G}_{\rm x} + \vec{F}_{\mu}.
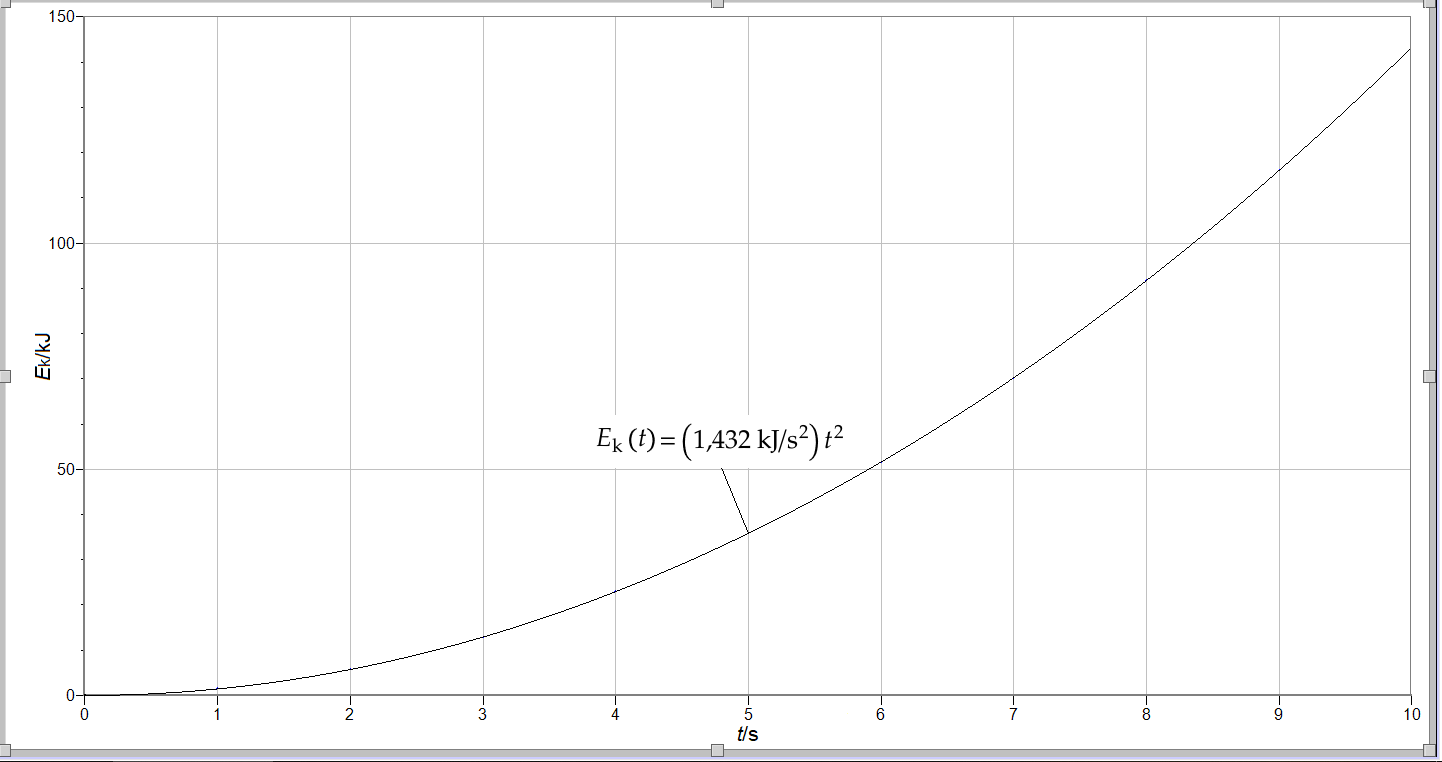
4.2 Johda lauseke, joka esittää lohkareen liike-energiaa ajan funktiona. Laadi johtamasi lausekkeen avulla graafinen esitys liike-energiasta ajan funktiona välillä 0–10 s. 7 p.
Lohkareen liike on tasaisesti muuttuvaa. Lohkareen nopeus on siis v(t)=v_0+at, jossa alkunopeus on v_0=0. Lohkareen liike-energiaksi saadaan E_k(t)=\tfrac{1}{2}m[v(t)]^2=\tfrac{1}{2}m(at)^2=\tfrac{1}{2}ma^2t^2=(1432\,{\rm kg\,m}^2/{\rm s}^4)t^2=({\rm 1,432}\,{\rm kJ/s}^2)t^2.
Kuvaaja:
Pisteytys:
On esitetty liike-energian suureyhtälö ajan ja kiihtyvyyden avulla joko käyttäen suuresymboleja tai lukuarvoa oikeilla yksiköillä. (2 p.)
On esitetty kuvaaja liike-energiasta ajan funktiona. Liike-energian arvon tulee olla luettavissa oikein kaikkina ajanhetkinä. Kuvaajan tulee vastata johdettua lauseketta. (5 p.)
-
Jos funktiona on jokin muu kuin paraabeli, kuvasta ei saa pisteitä.
-
Jos funktiota kuvaava yhtenäinen viiva puuttuu tai se näkyy liian karkeana murtoviivana, vähennetään kolme pistettä.
-
Jos kuvaaja on piirretty ajan neliön funktiona, vähennetään kolme pistettä.
-
Jos akselin lukuarvot ovat väärin tai puuttuvat, vähennetään kaksi pistettä.
-
Jos esitetty kuvaaja on piirretty muulle kuin kysytylle aikavälille, vähennetään kaksi pistettä.
-
Jos suureen lukuarvot tai tunnus puuttuu tai on väärin vähennetään kaksi pistettä.
-
Jos suureen yksikkö puuttuu tai akselit ovat väärin päin, vähennetään kummastakin virheestä yksi piste.
Tyypillisiä virheitä:
-
Tehdään virhe liike-energian suureyhtälössä tai se yksiköissä tai jätetään se kirjoittamatta kiihtyvyyden ja ajan avulla.
-
Piirretään kuvaajaa negatiiviselle ajalle.
5. Mars ja sen kuut 15 p.
5.1 Laske Phobosin ja Deimosin välisen voiman suuruus, kun ne ovat lähimpänä toisiaan. Laske myös Mars-planeetan ja Deimosin välisen voiman suuruus. Mikä on voimien suuruuksien suhde? 6 p.
Lyhin etäisyys Phobosin ja Deimosin välillä on R = rD - rP, missä rD on Deimosin kiertoradan säde ja rP Phobosin kiertoradan säde. Tällä etäisyydellä ne vetävät toisiaan puoleensa voimalla G_{\rm DP}=\gamma m_{\rm D}m_{\rm P}/R^2, kun m_\rm P = 1,08 \cdot 10^{16} \rm{kg} ja m_\rm D = 1,80 \cdot 10^{15} \rm{kg} ovat Phoboksen ja Deimoksen massat.
Mars ja Deimos ovat jatkuvasti etäisyydellä rD toisistaan ja vetävät toisiaan puoleensa voimalla G_{\rm DM}=\gamma m_{\rm D}m_{\rm M}/r_{\rm D}^2, kun m_\rm M = 6{,}417 \cdot 10^{23} \rm{kg} on Marsin massa.
Sijoittamalla lukuarvot aineistosta 5.A ja gravitaatiovakio (\gamma = 6,67428\cdot 10^{-11}\,{\rm Nm}^2/{\rm kg}^2) saadaan lukuarvot G_{\rm DP}=6,53921\cdot 10^{6}\,{\rm N}\approx 6{,}54\cdot 10^{6}\,\mathrm{N} ja G_{\rm DM}=1{,}40037\cdot 10^{14}\,{\rm N}\approx 1{,}40\cdot 10^{14}\,\mathrm{N}. Voimien suuruuksien suhteeksi saadaan G_{\rm DM}/G_{\rm DP}=2,14\cdot 10^7 tai sen käänteisluku 4,67\cdot 10^{-8}.
Pisteytys:
On esitetty suureyhtälö gravitaatiovoimalle ja hyödynnetty sitä ratkaisussa. (2 p.)
On annettu oikea vastaus Phoboksen ja Deimoksen väliselle voimalle 2 – 3 merkitsevän numeron tarkkuudella. (2 p.)
On annettu oikea vastaus Marsin ja Deimoksen väliselle voimalle 2 – 3 merkitsevän numeron tarkkuudella. (1 p. )
On annettu oikea vastaus voimien suhteelle 2 – 3 merkitsevän numeron tarkkuudella. (1 p.)
Tyypillinen virhe: Ei ole huomattu, että Phoboksen ja Deimoksen massat on annettu vain kolmen merkitsevän numeron tarkkuudella ja on käytetty vastauksissa liikaa merkitseviä numeroita.
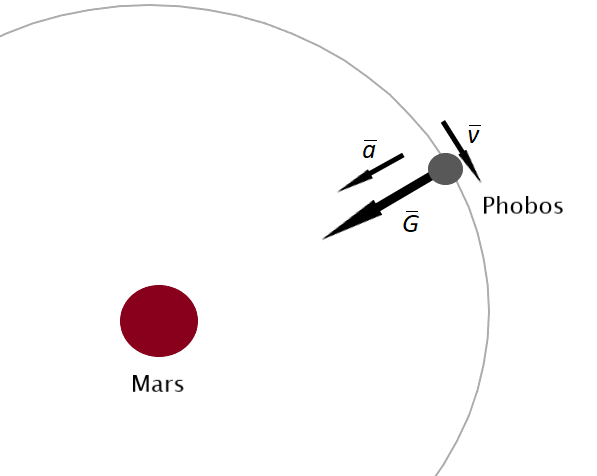
5.2 Piirrä Phobosin voimakuvio ja määritä Marsin massa Phobosin kiertoradan ominaisuuksien perusteella. Määritä sitten Marsin massa Deimosin kiertoradan ominaisuuksien perusteella. Miten tarkasti voit saamiesi tulosten perusteella ilmoittaa Marsin massan? 9 p.
Phobokseen kohdistuu vain Marsin aiheuttama painovoima G. Deimoksen aiheuttama painovoima GDP on häviävän pieni osatehtävän 5.1 perusteella ja sen suunta muuttuu koko ajan kuiden kiertäessä Marsia.
Mars ja Phobos vetävät toisiaan voimalla G_{\rm PM}=\gamma m_{\rm P}m_{\rm M}/r_{\rm P}^2.
Tämä voima aiheuttaa Phobosille keskeiskiihtyvyyden an, koska se on ainoa Phobosiin kohdistuva voima. Newtonin II lain mukaisesti G_{\rm PM}=m_{\rm P}a_n.
Toisaalta ympyräliikkeen keskeiskiihtyvyys saadaan kaavasta a_n=v^2/r_{\rm P}.
Kiertoaika TP on vakio, joten ratanopeus v = 2 \pi r_{\rm P} / T_{\rm P} on vakio ja keskeiskiihtyvyydeksi saadaan a= 4 \pi^2 r_{\rm P} /T_{\rm P}^2 . Kirjoittamalla liikeyhtälö tämän avulla muotoon m_{\rm P} 4 \pi^2 r_{\rm P} /T_{\rm P}^2 =\gamma m_{\rm P}m_{\rm M}/r_{\rm P}^2 voidaan ratkaista Marsin massan yhtälöksi m_{\rm M}=4\pi^2 r_{\rm P}^3/(\gamma T_{\rm P}^2). Sijoittamalla lukuarvot saadaan Marsin massalle arvio m_{\rm M}=6,4205\cdot 10^{23}\,{\rm kg.}
Tekemällä vastaava lasku käyttäen Deimosin ratasädettä ja kiertoaikaa saadaan Marsin massan suureyhtälöksi m_{\rm M}=4\pi^2 r_{\rm D}^3/(\gamma T_{\rm D}^2) ja massalle arvio m_{\rm M}=6,4163\cdot 10^{23}\,{\rm kg.}
Kahden saadun arvion nähdään täsmäävän kolmen numeron tarkkuudella, joten Marsin massaksi voidaan ilmoittaa m_{\rm M}=6,42\cdot 10^{23}\,{\rm kg.} Luku täsmää aineiston ja MAOL-taulukon kanssa.
Pisteytys:
On esitetty voimakuvio, jossa Phobokseen on piirretty vain gravitaatioksi nimetty voimanuoli, joka osoittaa Marsin suuntaan (2 p.)
-
Jos voimanuoli on irti Phoboksesta tai Phobokseen on piirretty kiinni muita nuolia, voimakuviosta ei anneta pisteitä.
-
Jos kuvasta ei käy ilmi missä suunnassa radan keskipiste tai Mars sijaitsee, voimakuviosta ei anneta pisteitä.
On perusteltu ratkaisu mainitsemalla Newtonin II laki ja kirjoitettu sen mukainen liikeyhtälö gravitaatiovoimaa käyttäen (2 p).
On esitetty oikea suureyhtälö Phoboksen ratanopeudelle (1 p.)
On esitetty suureyhtälö Marsin massalle ja sen perusteella laskettu Marsin massa (2 p.)
On vastattu kysymykseen "Miten tarkasti" joko ilmoittamalla merkitsevien numeroiden lukumäärä tai massaväli (2 p.)
Tyypillisiä virheitä:
-
Piirretään nopeutta tai kiihtyvyyttä kuvaava voimanuoli kiinni Phobokseen.
-
Tehdään vertailua pelkästään Marsin massan kirjallisuusarvoon.
6. Millikanin koetta mukaillen 15 p.
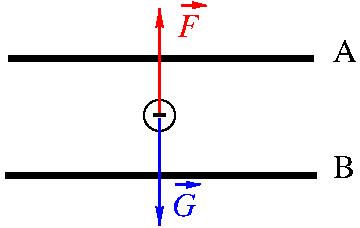
6.1 Piirrä pisaran voimakuvio. Kumpi levy, A vai B, on negatiivisesti varautunut? Perustele. 5 p.
Pisara on tasapainossa. Paino \vec{G} osoittaa alaspäin. Sähköisen voiman \vec{F} täytyy siis osoittaa ylöspäin. Koska pisara on negatiivisesti varautunut, alemman levyn B tulee olla negatiivinen ja ylemmän positiivinen, jotta pisaraan kohdistuva sähköinen voima osoittaisi ylöspäin.
Vastaus: B
Pisteytys:
On esitetty voimakuvio, jossa pisaraan on piirretty kaksi nimettyä voimanuolta oikeisiin suuntiin. (2 p.)
-
Sähköisen voiman voi kuvata myös kummankin levyn aiheuttamalla voimalla, jos asian selittää tekstissä.
-
Jos voimanuoli on irti pisarasta tai pisaraan on piirretty kiinni muita nuolia, voimakuviosta ei anneta pisteitä.
-
Jos voimakuvioon on piirretty nopeutta tai kiihtyvyyttä kuvaava nuoli, kuvasta ei anneta pisteitä.
-
Jos voimanuolet ovat selvästi eri pituisia, vähennetään yksi piste.
On annettu oikeana vastauksena levy B (1 p.) ja perusteltu vastaus oikein (2 p.).
Tyypillisiä virheitä:
-
Pisaraan piirretyt voimanuolet eivät tuota tasapainotilannetta.
-
On tarkasteltu vain toisen levyn ja pisaran välistä vuorovaikutusta.
-
Ei ole mainittu ylöspäin olevan voiman olevan sähköinen voima.
6.2 Kuinka monta ylimääräistä elektronia öljypisarassa on? 10 p.
Pisara on pallon muotoinen, joten sen massa m=\tfrac{4}{3}\pi r^3\rho, jossa r on pisaran säde ja ρ sen tiheys. Pisaran paino on näin ollen \vec G=m \vec g=\tfrac{4}{3}\pi r^3\rho \vec g.
Koska pisarassa on varaus, siihen vaikuttaa sähköinen voima \vec F=q\vec E, jossa q on pisaran nettovaraus ja E on alaspäin osoittavan sähkökentän voimakkuus.
Pisaran leijuessa ovat voimat yhtä suuret, \vec F+\vec G=0.
Kondensaattorilevyjen välissä olevalle sähkökentälle pätee E= \frac{U}{d} , jossa U on jännite ja d levyjen välinen etäisyys.
Tasapainotilanteessa painovoima ja sähköinen voima ovat yhtäsuuret ja vastakkaissuuntaiset, joten\frac{qU}{d}=\frac{4}{3}\pi r^3\rho g. Ratkaistaan varaus: q=\frac{4d\pi r^3\rho g}{3U}.
Sijoittamalla lukuarvot saadaan varauksen itseisarvolle │q│= 1,631057 · 10-18 C.
Pisara on edellisen kohdan mukaan negatiivisesti varautunut, joten q = -1,631057 · 10-18 C. Pisaran varauksen suhde yhden elektronin varaukseen on \frac{q}{-e}\approx10{,}18.
Pyöristetään lähimpään kokonaislukuun, koska varauksen on oltava alkeisvarauksen e=1{,}60\cdot10^{-19} \rm C monikerta.
Vastaus: 10 elektronia.
Pisteytys:
On esitetty pisaralle oikea tasapainoyhtälö tai liikeyhtälö. (2 p.)
On esitetty pisaran painon tai massan suureyhtälö tiheyden avulla tai määritetty massa tai paino oikein. (2 p.)
On esitetty sähköisen voiman suureyhtälö potentiaalieron ja levyjen välimatkan avulla. (2 p.)
On esitetty oikea suureyhtälö pisaran varaukselle tai pisarassa olevin elektronien lukumäärälle. (2 p.)
On annettu oikea vastaus kokonaislukuna. (2 p.)
Tyypillisiä virheitä: Annetaan vastaus desimaalilukuna.
7. Sähkölukko 15 p.
Ovessa oleva sähkölukko avataan viemällä kulkutunniste lähelle lukulaitetta (kuva ). Lukulaite luo ympärilleen magneettikentän, jossa tunniste aktivoituu ja oikean tunnisteen tapauksessa lukulaite avaa lukon.
Tunnisteen sijasta lukulaitteen pinnalle asetettiin käämi. Sen johtimien päiden välille oli kytketty vastus, jonka resistanssi oli 330 Ω kuvan mukaisesti. Tällöin oskilloskoopin avulla mitattiin vastuksen napojen välillä korkeataajuinen sinimuotoinen vaihtojännite, jonka amplitudi oli 1,2 V. Käämin oma resistanssi oli pieni, eikä käämi liikkunut mittauksen aikana.
7.1 Selitä miten vastuksen napojen välinen jännite syntyy. 4 p.
Lukulaite luo ajassa muuttuvan magneettikentän. Käämin läpäisevä magneettivuo muuttuu ajassa ja induktiolain mukaan käämiin indusoituu jännite, joka havaitaan vastuksen päiden välillä.
Pisteytys:
On tunnistettu, että lukulaite synnyttää muuttuvan magneettikentän. (2 p.)
On kerrottu, että vastuksen napojen välinen jännite johtuu käämiin indusoituvasta jännitteestä. (2 p.)
Tyypillinen virhe: On väitetty, että käämiin indusoituu sähkövirta, joka saa aikaan jännitteen. Tämä vastaus ei tuota pisteitä jännitteen syntymisestä.
7.2 Käämiin kytketty vastus korvattiin toisella vastuksella, jonka resistanssi oli 1,0 kΩ. Kuinka suuri oli vaihtojännitteen amplitudi tämän vastuksen napojen välillä? Perustele vastauksesi. 4 p.
Indusoitunut jännite riippuu induktiolain mukaan vain käämin ja kentän ominaisuuksista. Jännitteen amplitudi ei muutu, vaan se on edelleen 1,2 V.
Pisteytys: On kerrottu perusteluna jännitteen riippuvan vain kentän ja käämin ominaisuuksista (2 p.) ja sen takia jännitteen pysyvän ennallaan (2 p.)
Tyypillisiä virheitä: Ajatellaan käämiin indusoituvan virran pysyvän vakiona ja jännitteen kasvavan 3,6 V:iin.
7.3 Käämiä siirrettiin kauemmaksi lukulaitteesta. Miksi mitatun jännitteen amplitudi pienenee? 4 p.
Magneettivuon tiheys on pienempi kauempana lukulaitteesta. Tällöin käämin läpäisevä magneettivuokin on pienempi ja siten sen muutosnopeus on pienempi. Induktiolain mukaisesti, indusoitunut jännite on pienempi.
Pisteytys: On mainittu, että magneettivuon tiheys pienenee, kun etäisyys lukulaitteesta kasvaa (2 p.), ja tämän seurauksena käämin läpäisevän magneettivuon muutokset ovat pienempiä ja aiheuttavat pienemmän induktiojännitteen. (2 p.)
Tyypillisiä virheitä:
-
Väitetään, että käämin paikka vaikuttaa siihen, kuinka suuren kentän lukulaite synnyttää.
-
Väitetään lukulaitteen synnyttämän magneettivuon tiheyden noudattavan suoran virtajohtimen magneettivuon tiheyden suureyhtälöä B = \mu_o I / 2 \pi r. Todellinen etäisyysriippuvuus ei ole näin yksinkertainen. Virheestä ei vähennetä pisteitä, jos vaaditut asiat on kerrottu oikein.
7.4 Kuvissa on esitetty kuusi mahdollista kuvaajaa magneettivuon tiheydelle B (paksu yhtenäinen viiva). Jokaiseen kuvaajaan on piirretty myös vastuksen napojen välinen jännite V (katkoviiva) vertailun helpottamiseksi. Mikä kuvaajista vastaa parhaiten magneettivuon tiheyttä ajan funktiona käämin kohdalla? 3 p.
-
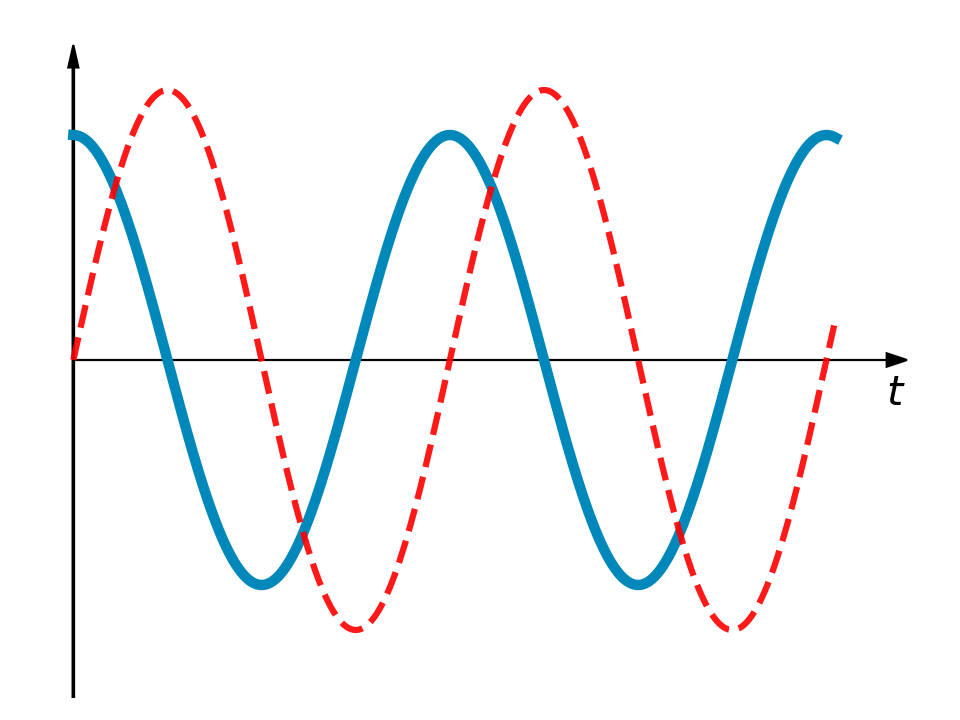 (3 p.)
(3 p.)
8. Ydinreaktioita varhaisessa maailmankaikkeudessa 15 p.
8.1 Laske, mikä oli neutronien osuus nukleoneista (R), kun maailmankaikkeuden lämpötila oli T=1,0\cdot 10^{10}\,{\rm K}. 5 p.
Tehtävässä tarvitaan tiedot
m_{\rm n}=1,67492747\cdot 10^{-27}\,{\rm kg} m_{\rm p}=1,67261898\cdot 10^{-27}\,{\rm kg} c=3,0\cdot 10^8\,{\rm m/s} k=1,380649\cdot 10^{-23}\,{\rm J/K} T=1,0\cdot 10^{10}\,{\rm K}
sekä neutronin ja protonin massojen erotus
\Delta m=m_{\rm n}-m_{\rm p}>0.
Käytetään aineistossa annettua yhtälöä
\frac{N_{\rm n}}{N_{\rm p}}=\exp\Bigl[-\frac{(m_{\rm n}-m_{\rm p})c^2}{kT}\Bigr]=0,2225\approx 0,22.
Näistä saadaan
R=\frac{N_{\rm n}}{N_{\rm n}+N_{\rm p}}=\frac{\frac{N_{\rm n}}{N_{\rm p}}}{\frac{N_{\rm n}}{N_{\rm p}}+1}=0,1820\approx 0,18.
Pisteytys:
On annettu kahden tai kolmen numeron tarkkuudella oikea lopputulos. (5 p.)
Jos lopputulos on väärin neutronien ja protonien suhteen oikeasta lukuarvosta saa kaksi pistettä.
Tyypillisiä virheitä: Annettu vastauksena neutronien ja protonien suhde tai protonien osuus nukleoneista.
8.2 Kirjoita reaktioyhtälö reaktiolle, jossa neutroni muuttuu protoniksi. 2 p.
Kysytty reaktio on {\rm n}+\nu_{\rm e}\to {\rm p}+{\rm e} tai {\rm n}\to {\rm p}+{\rm e}+\bar\nu_{\rm e}.
Pisteytys:
On kirjoitettu toinen oikeista reaktioyhtälöistä. (2 p.)
-
Neutriino saa puuttua tai sekoittua sen antihiukkaseen.
-
Protonia voi merkitä vedyn symbolilla.
Tyypillisiä virheitä: Merkitty vety-ytimelle jokin väärä massaluku.
8.3 Kirjoita reaktioiden ketju, jossa protoneista ja neutroneista lopulta syntyy helium-4-ydin. Ketjun tulee olla sellainen, että kussakin reaktioyhtälössä vasemmalla puolella on vain kaksi hiukkasta tai ydintä. 3 p.
Helium-4:n tuottaminen onnistuu esimerkiksi seuraavasti: ensin tuotetaan kaksi deuteronia D kahdella reaktiolla {\rm p}+{\rm n}\to {\rm D} ja sitten niistä heliumydin reaktiolla {\rm D}+{\rm D}\to {\rm ^4He}.
Pisteytys:
On kirjoitettu oikein ensimmäinen reaktioyhtälö (1 p.) ja loput tarvittavat reaktioyhtälöt (1 p.) sekä ilmoitettu, mikäli jotain reaktioista tarvitaan useampia kuin yksi. (1 p.)
-
Jos ensimmäinen reaktioyhtälö on väärin, osatehtävästä ei voi saada pisteitä.
-
Jos reaktioyhtälön vasemmalla puolella on yksi tai enemmän kuin kaksi hiukkasta, reaktioyhtälöstä ei saa pisteitä.
-
Myös muut kuin yllä mainittu protoneista ja neutroneista lähtevät reaktioketjut, jotka tuottavat \rm{^4He}-ytimen, antavat oikean vastauksen pisteet.
Tyypillisiä virheitä: Merkitty vety-ytimille jokin väärä massaluku.
8.4 Tarkastele aineiston kuvaa. Mitä voidaan kuvan perusteella päätellä sen esittämästä teoreettisesta mallista suhteessa havaintoihin? Arvioi karkeasti heliumin ja vedyn massaosuuksien suhde kuvan havaintoja vastaavasta kohdasta. 5 p.
Aineiston kuvaaja esittää kevyiden ydinten massaosuuksia S tiheyden D funktiona. Kumpikin akseli on suhteellinen. Pystysuoran viivan ja käyrien leikkauspisteet kuvaavat WMAP-satelliitin havaintoja. Kuvaajasta nähdään, että alkuräjähdysteoriaan perustuva teoreettinen malli ennustaa kevyiden isotooppien havaitut suhteelliset osuudet avaruudessa hyvin.
Jos M_1 on vedyn massaosuus ja M_2 on heliumin massaosuus, niin kuvan perusteella ^4He-käyrältä luettu leikkauspiste antaa suoraan kysytyn massaosuuksien suhteen käänteisluvun, sillä massaosuudet on normitettu vety-ydinten massaosuuteen S_{\rm 0}. \frac{M_1}{M_2}\approx \frac{1}{0,2}=5.
Pisteytys:
On kerrottu, että malli ennustaa hyvin kevyiden isotooppien osuudet avaruudessa. (3 p.)
On annettu vastauksena yhden tai kahden merkitsevän numeron tarkkuudella oikea massaosuuksien suhde. (2 p.)
Tyypillisiä virheitä: Selitetty kuvasta isotooppien massaosuuksien muutosta ajan tai tiheyden funktiona.
Osa 3: 20 pisteen tehtävät
9. Trampoliini 20 p.
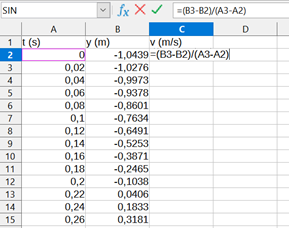
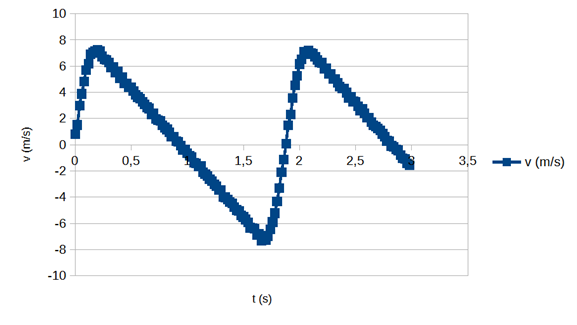
9.1 Selitä, miten taulukon perusteella voidaan laskea fyysikon nopeus. Piirrä kuvaaja, joka esittää fyysikon nopeutta kaikilla taulukon ajan hetkillä. 6 p.
Paikan mittaus on tehty tasaisella aikavälillä \Delta t=20\,{\rm ms}. Lasketaan keskinopeus v=\frac{\Delta y}{\Delta t} jokaiselle aikavälille. Vaihtoehtoisesti paikkadata voidaan derivoida ajan suhteen esimerkiksi LoggerPro-ohjelmalla.
Piirretään näin saatu nopeusdata ajan funktiona.
Kuvaaja:
Pisteytys:
On kerrottu, että nopeus saadaan kunkin aikavälin keskinopeutena tai derivoimalla paikan aikariippuvuutta tai näytetty mittausaineiston derivointi graafisesti tai taulukossa. (2 p.)
On esitetty kuvaaja fyysikon nopeudesta ajan funktiona. (4 p.)
-
Jos kuvaaja ei esitä oikeaa nopeutta, kuvaajasta ei anneta pisteitä.
-
Jos suureiden symbolit tai nimet tai yksiköt puuttuvat tai ovat väärin, vähennetään yksi piste.
Tyypillisiä virheitä:
-
Mittauspisteisiin on sovitettu harmoninen funktio.
-
On laskettu paikka- ja aikasarakkeiden suhde \frac{v}{t} tai tulo v\cdot t ja käytetty tätä nopeutena.
9.2 Mikä liikkeen malli kuvaa fyysikon liikettä ajan hetkellä t = 0,1\,{\rm s}? 1 p.
- harmoninen värähdysliike (1 p.)
9.3 Mikä liikkeen malli kuvaa fyysikon liikettä ajan hetkellä t = 0,5\,{\rm s}? 1 p.
- tasaisesti kiihtyvä liike (1 p.)
9.4 Millä ajan hetkellä liikkeen tyyppi muuttuu seuraavan kerran ajanhetken t = 0,5\,{\rm s} jälkeen? 1 p.
- 1,7 s (1 p.)
9.5 Määritä fyysikon suurin kiihtyvyys. 4 p.
Fyysikon suurin kiihtyvyys saavutetaan pisteessä, jossa nopeuden kulmakerroin on suurin. Kiihtyvyys saadaan kuvaajan tangentista tällaisessa pisteessä. Vaihtoehtoisesti voidaan derivoida data toistamiseen ajan suhteen ja lukea uudesta kuvaajasta maksimikiihtyvyys. Fyysikon suurin kiihtyvyys on 55–58 m/s2.
Pisteytys:
On kerrottu, että kiihtyvyys saadaan derivoimalla nopeuden aikariippuvuutta tai näytetty mittausaineiston derivointi graafisesti tai käytetty nopeuskuvaajan tangenttia. (2 p.)
On annettu vastauksena kahden tai kolmen merkitsevän numeron tarkkuudella oikea kiihtyvyys välillä 55 \rm{m/s^2} — 60 \rm{m/s^2} (2 p.)
Tyypillisiä virheitä:
-
On piirretty nopeutena paikka- ja aikasarakkeiden suhde ja etsitty tästä suurinta kiihtyvyyttä.
-
On piirretty paikan aikariippuvuus ja käytetty tähän piirretyn tangentin kulmakerrointa suurimman kiihtyvyyden arvona.
9.6 Johda lauseke suurimmalle amplitudille A jolla fyysikon jalat eivät irtoa trampoliinilta. Käytä apunasi tekstiä . Mikä on suurin mahdollinen amplitudi, jolla jalat eivät irtoa trampoliinilta, jos fyysikon massa on 68 kg ja trampoliinin "jousivakio" on 4 600 N/m? 7 p.
Suurin amplitudi voidaan ratkaista joko paikasta tai voimien avulla. Värähdysliikkeessä paikka on tekstin 9.B mukaisesti
y(t)=-\frac{mg}{k}-A\cos 2\pi ft.
Koska trampoliini ei kohdista hypääjään voimaa alaspäin, harmonisessa liikkeessä paikka voi olla korkeintaan kuormittamattoman trampoliinin taso y = 0. Siten
-\frac{mg}{k}-A\cos2\pi ft \leq 0.
Paikan suurin arvo saavutetaan sellaisella ajanhetkellä t kun \cos\left(2\pi ft\right)=-1. Tällöin -\frac{mg}{k}+A\ =\ 0, joten amplitudiksi saadaan
A=\frac{mg}{k}.
Vaihtoehtoisesti voidaan todeta, että tasapainoasemassa
\Sigma F=-ky_0-mg=0.
Tällöin tasapainoasema on
y_0=-\frac{mg}{k}.
Hyppijä irtoaa trampoliinista, kun \cos(2\pi f t)=-1 jolloin jousivoima
F_j=-ky=0.
Tästä syystä suurin mahdollinen amplitudi on tasapainoaseman etäisyys kuormittamattoman trampoliinin nollatasosta
A=|y_0|=\frac{mg}{k}.
Annetulla massan ja "jousivakion" k arvolla,
A=\frac{68\,{\rm kg}\cdot 9,81\,{\rm m}/{{\rm s}^2}}{4600\,{\rm N/m}}=0,15\,{\rm m}.
Pisteytys:
On perusteltu ratkaisu oikein käyttäen joko voimatarkastelua tai värähdysliikettä ja tasapainoasemaa. (3 p.)
On kirjoitettu ratkaistu suureyhtälö amplitudille (2 p.) ja annettu kahden tai kolmen merkitsevän numeron tarkkuudella oikea amplitudi välillä 0,14 m – 0,15 m. (2 p.)
Tyypillisiä virheitä: On ratkaistu aineistossa annetusta värähdysliikkeen paikan yhtälöstä A ja sijoitettu siihen tavalla tai toisella pääteltyjä lukuarvoja.
10. Vesipullo 20 p.
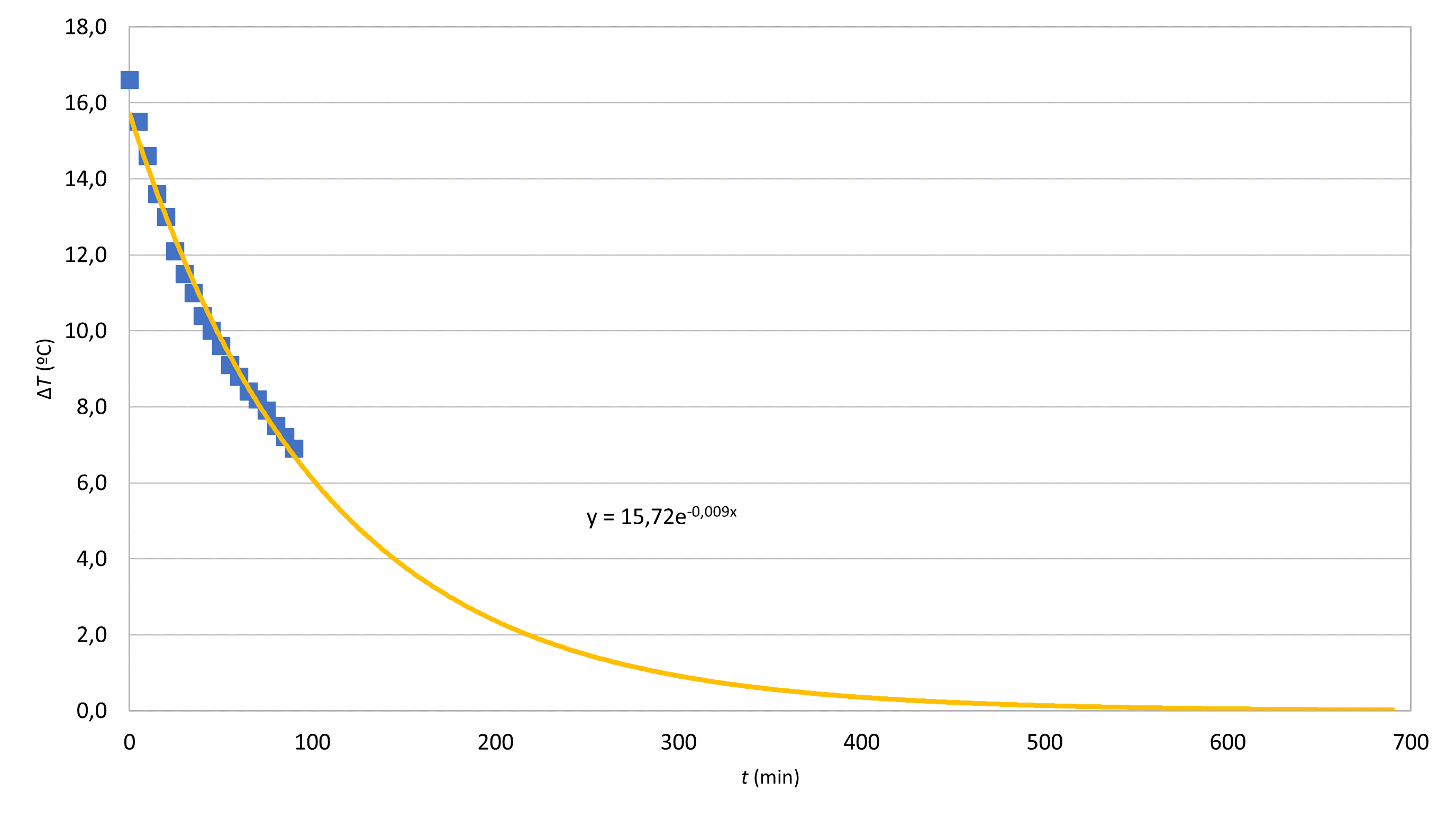
10.1 Laadi graafinen esitys, josta ilmenee veden (taulukko ) ja huoneen lämpötilaero ajan funktiona. Kuinka pitkän ajan kuluessa veden lämpötila olisi mittaustarkkuuden rajoissa saavuttanut huoneen lämpötilan? 7 p.
Ekstrapoloimalla (tai sovitetusta funktiosta) todetaan, että sovitusfunktion arvo pienenee alle 0,05 °C noin 580–610 minuutissa. Lämpötilaero siis saavuttaa nollan lämpömittarin 0,1 °C:n tarkkuudella noin 580–610 minuutin jälkeen.
Pisteytys:
On esitetty kuvaaja, jossa lämpötilaeroa ajan funktiona kuvaavat pisteet näkyvät erillisinä mittauspisteinä. (3 p.)
-
Jos kuvaajassa on piirretty lämpötila lämpötilaeron sijaan, kuvaajasta ei saa pisteitä.
-
Jos mittauspisteet eivät erotu, vähennetään yksi piste.
-
Jos kuvaajassa näkyy kaksi erilaista sovitetta tai sovite ja murtoviiva, vähennetään yksi piste.
-
Jos suureen tunnus puuttuu tai yksikkö puuttuu tai akselit ovat väärin päin, vähennetään kustakin virheestä yksi piste.
On esitetty sovitefunktiona eksponenttifunktio ja näytetty sen lauseke. (2p.)
On annettu vastauksena 1 – 3 merkitsevän numeron tarkkuudella aika välillä 580 min – 610 min. (2 p.)
Tyypillinen virhe: Väärän sovitefunktion käyttäminen.
10.2 Vesipullo laitettiin takaisin jääkaappiin 1,5 tunnin jälkeen. Jääkaappi jäähdytti ideaalisella suorituskyvyllä, eli \varepsilon_{\rm max}=\frac{Q}{W}=\frac{1}{\eta_{\rm max}}-1, jossa Q on siirtynyt lämpömäärä, W on työ ja \eta_{\rm max} on ideaalinen hyötysuhde. Kuinka paljon ylimääräistä sähköenergiaa kului, kun vesi jäähtyi takaisin jääkaapin lämpötilaan? 5 p.
Mittausaineistosta: \Delta T_{\rm 90\,min}=15,0\,^\circ{\rm C}-5,3\,^\circ{\rm C}=9,7\,^\circ{\rm C}.
1,5 tunnin aikana vesi on lämmennyt 9,7\,^\circ{\rm C}, eli vesi on vastaanottanut lämpömäärän Q=cm\Delta T=20,04288\,{\rm kJ}\approx 20\,{\rm kJ}, jossa veden ominaislämpökapasiteetti c = 4,1819 kJ/(kg·K) ja massa m=\rho V=998,20\,\frac{\rm kg}{{\rm m}^3}\cdot 0,5\,{\rm dm}^3. Suorituskyky saadaan määritettyä ideaalisesta hyötysuhteesta: \varepsilon_{\rm max}=\frac{Q}{W}=\frac{1}{\eta_{\rm max}}-1=\frac{T_2}{T_1-T_2}\approx 16,77410, jossa T_1=273,15\,{\rm K}+21,9\,{\rm K} ja T_2=273,15\,{\rm K}+5,3\,{\rm K}.
Jääkaapin kuluttama sähköenergia on W=\frac{Q}{\varepsilon_{\rm max}}=cm\Delta T \frac{T_1-T_2}{T_2}=1,19487\,{\rm kJ}\approx 1,19\,{\rm kJ}.
Pisteytys:
On annettu vastauksena 2 – 3 merkitsevän numeron tarkkuudella sähköenergia välillä 1190 J – 1230 J. (5 p.) Jos vastaus väärin, annetaan oikein lasketusta vedestä pois siirtyneenlämpömäärän arvosta Q = 20 kJ kaksi pistettä ja oikein lasketusta suorituskyvyn arvosta \varepsilon = 16{,}8 kaksi pistettä.
Tyypillisiä virheitä:
-
Väärien lämpötilojen käyttäminen veteen siirtyneen lämmön laskemisessa.
-
Väärien lämpötilojen tai Celsius-asteiden käyttäminen suorituskykyä laskiessa.
10.3 Samanlainen tyhjä pullo laitettiin jääkaappiin huoneenlämpöisenä ja odotettiin, kunnes se saavutti jääkaapin lämpötilan. Pullo alkoi jäähtyessään rutistua kasaan, kun pullon ja ulkoisen ilman paine-ero kasvoi 2,0 millibaariin (kuva ). Määritä pullossa olevan ilman tilavuuden muutoksessa tehty työ, kun paine-ero pysyi vakiona muutoksen aikana. Selitä, miten pullon rutistuminen vaikutti pullossa olevan ilman jäähtymiseen verrattuna siihen, että pullo ei rutistuisi. 8 p.
Pullossa olevan ilman voidaan olettaa käyttäytyvän kuten ideaalikaasu, eli voidaan käyttää ideaalikaasun tilanyhtälöä: pV=nRT.
Ainemäärä n säilyy, joten \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}, josta saadaan lopullinen tilavuusero: \Delta V = V_1-\frac{p_1V_1T_2}{T_1p_2}=V_1\Bigl(1-\frac{p_1T_2}{T_1(p_1-\Delta p)}\Bigr)
Alkuperäinen tilavuus oli V_1=0,5\,{\rm dm}^3 , paine p_1=101325\,{\rm Pa} , paine-ero \Delta p=2,0\,{\rm mbar}=200\,{\rm Pa} ja lämpötilat olivat T_1=21,9\,{^\circ}{\rm C}=295,05\,{\rm K} ja T_2=5,3\,{^\circ}{\rm C}=278,45\,{\rm K} , jolloin \Delta V=0,0271976\,{\rm dm}^3 eli noin 5,4 % alkuperäisestä tilavuudesta.
Paine pysyy muuttamattomana koko puristuksen aikana, jolloin työ on W=p_2\Delta V=(p_1-\Delta p)\Delta V=(p_1-\Delta p)V_1\Bigl(1-\frac{p_1T_2}{T_1(p_1-\Delta p)}\Bigr)=V_1\Bigl((p_1-\Delta p)-p_1\frac{T_2}{T_1}\Bigr). W=2,750356\,{\rm J}\approx 2,75\,{\rm J}.
Pullossa olevaan ilmaan tehdään työtä. Lämpöopin ensimmäisen pääsäännön mukaan työ kasvattaa pullossa olevan ilman sisäenergiaa, jota ilman jäähtyminen samaan aikaan vähentää. Tästä syystä pullossa olevasta ilmasta täytyy sen jäähtyessä siirtyä pois suurempi lämpömäärä. Jäähtymiseen kuluu enemmän aikaa kuin tilanteessa, jossa ilma olisi vakiotilavuudessa.
Pisteytys:
Ideaalikaasun tilanyhtälö on mainittu ja sitä on käytetty ratkaisussa. (2 p.)
Ainemäärän säilyminen on mainittu tai ainemäärän symboli näkyy ja ainemäärän säilymistä on käytetty ratkaisussa. (2 p.)
On annettu vastauksena 2 – 3 merkitsevän numeron tarkkuudella oikein ratkaistu työ. (2 p.)
On vastattu käyttäen termodynamiikan 1. pääsääntöä tai lämmön ja työn käsitteitä ilman ristiriitaa joko jäähdyttämiseen tarvittavan ajan kasvaminen tai tarve siirtää suurempi lämpömäärä pois pullosta. (2 p.)
Tyypillisiä virheitä: Jätetty paineen muutos huomiotta laskettaessa pullon tilavuuden muutosta tai rutistystyötä.
11. Työselostus 20 p.
Lukiolaiset tekivät kokeellista tutkimusta jousivoimasta ja tuottivat tekemästään työstä työselostuksen (aineisto ).
Arvioidessaan työselostusta opettaja jakoi sen katkoviivoin viiteen numeroituun osaan. Jokaisessa osassa on yksi tai useampia virheitä. Tehtäväsi on löytää jokaisesta osasta sen fysikaalisesti merkittävin yksittäinen virhe ja kertoa, miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein. Huomaa, että jokaisen osatehtävän vastauksessa tulee olla mainittuna vain yksi virhe.
Jokaisen osatehtävän vastauksessa saa olla mainittuna vain yksi virhe. Ehdotetun korjauksen tulee koskea tätä virhettä.
Kaikki osatehtävät pisteytettiin seuraavan ohjeen mukaisesti:
Vastauksessa on tunnistettu oikea virhe. (2 p.)
Jos vastauksessa on mainittu useampi kuin yksi virhe, virheen tunnistamisesta ei anneta pisteitä, ellei vastauksesta yksikäsitteisesti käy ilmi, mitä virheistä pidetään merkittävimpänä.
Vastauksessa on kuvattu oikea menettely virheen korjaamiseksi. (2 p.)
Jos vastauksessa on kuvattu muiden virheiden korjaukseen liittyviä toimenpiteitä, pisteitä ei anneta.
Kaikkiin osatehtäviin liittyi kaksi tyypillistä virhettä: (i) Mainitaan useampi kuin yksi virhe. (ii) On kuvattu virhe, mutta ei vastata kysymykseen "Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein?"
11.1 Mikä on työselostuksen osan 1 merkittävin virhe? Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein? 4 p.
Merkittävin virhe: Mittaukset suoritettiin (taulu)viivaimella, joka on lukematarkkuudeltaan turhan karkea.
Oikea menettely: Mittaukset tehdään mitalla, jota voi lukea 1 mm:n tarkkuudella, esimerkiksi rullamitalla tai viivoittimella.
Tyypillinen virhe: Väitetään merkittävimmäksi virheeksi kuminauhan lepopituuden väärää arvoa.
11.2 Mikä on työselostuksen osan 2 merkittävin virhe? Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein? 4 p.
Merkittävin virhe: Katkennut kuminauha korvattiin toisella, mutta mittauksia ei aloitettu uudelleen alusta.
Oikea menettely: Mittaussarja aloitetaan uudelleen alusta kuminauhan katkettua, koska kuminauhoissa saattaa olla yksilöllisiä eroja / koko mittaussarjassa käytetään samaa kuminauhaa.
Tyypillinen virhe: Väitetään merkittävimmäksi statiivin kaatumista tai puristimen irtoamista.
11.3 Mikä on työselostuksen osan 3 merkittävin virhe? Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein? 4 p.
Merkittävin virhe: Kuvaajassa on piirretty origoon ylimääräinen mittauspiste, jota ei vastaa mikään todellinen mittaustulos / on ajateltu, että kuminauhan pituus ilman venyttävää voimaa on nolla.
Oikea menettely: Kuvaajaan ei lisätä ylimääräistä pistettä, vaan esitetään vain todelliset mittauspisteet. Kuvaaja olisi parempi piirtää kuminauhan venymästä kuin sen pituudesta, mutta tämä ei ole sinänsä virhe, sillä jousivakio on määritettävissä kummallakin tavalla.
Tyypillinen virhe: Väitetään merkittävimmäksi virheeksi sitä, että graafissa vaaka-akselina on pituus venymän sijaan.
11.4 Mikä on työselostuksen osan 4 merkittävin virhe? Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein? 4 p.
Merkittävin virhe: Tulos (jousivakio) laskettiin yksittäisestä mittauspisteparista.
Oikea menettely: Mittausdataa hyödynnetään jousivakion määrittämisessä laajemmin, esimerkiksi kuvaajan kulmakertoimen avulla.
Tyypillinen virhe: Väitetään merkittävimmäksi virheeksi kuminauhan väristä puhumista.
11.5 Mikä on työselostuksen osan 5 merkittävin virhe? Miten virheen tekemisen sijasta toimitaan tai kuvataan toiminta työselostuksessa oikein? 4 p.
Merkittävin virhe: Tulokset yleistettiin koskemaan kaikkia venytyspituuksia.
Oikea menettely: Työselostuksessa ilmoitetaan, että tulos pätee vain rajallisella venymäalueella.
Tyypillinen virhe: Väitetään merkittävimmäksi virheeksi huonoa viittauskäytäntöä.