Beskrivningar av goda svar: SV – Fysik
24.9.2024
Slutgiltiga beskrivningar av goda svar 14.11.2024
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
De allmänna riktlinjerna för poängsättning är:
- Ifall att antalet gällande siffror som ges i svaret avviker från det som anges i BGS är avdraget en poäng för varje svar.
- Om enheten för slutresultatet är felaktig eller saknas är resultatet felaktigt.
Del 1: 20-poängsuppgift
1. Flervalsuppgifter från olika delområden i fysiken 20 p.
Välj det alternativ som passar bäst för varje situation i deluppgifterna. Rätt svar ger 2 p., fel svar 0 p. och inget svar 0 p.
1.1 Då en isbit smälter i ett glas vatten 2 p.
- förändras inte nivån på vattenytan. (2 p.)
1.2 Det talas mycket om smältande glaciärer. Då en glaciär smälter 2 p.
- binder den värme från atmosfären och sänker den omgivande luftens temperatur. (2 p.)
1.3 Då en gitarrsträng vibrerar 2 p.
- har den en nod i vardera ändan. (2 p.)
1.4 En gitarrsträng som är fäst i båda ändarna vibrerar fritt, och från den uppstår en ljudvåg som framskrider i luften. Då gitarrsträngens vibrationsfrekvens ökar till det dubbla 2 p.
- förändras inte ljudets hastighet i luften. (2 p.)
1.5 Då ett motstånd är kopplat till polerna på ett batteri gäller inuti motståndet att 2 p.
- den elektriska strömmens riktning är motsatt till elektronernas färdriktning, så att elektronerna färdas från batteriets negativa pol till dess positiva pol. (2 p.)
1.6 Då ett motstånd på 1,5 kΩ är kopplat till polerna på ett batteri på 1,5 V är spänningen mellan motståndets poler 1,5 V. Man håller kvar det första motståndet och kopplar sedan till polerna på samma batteri ytterligare två motstånd på 1,5 kΩ som sinsemellan är kopplade i serie. Spänningen mellan polerna på det första motståndet är då 2 p.
- 3,0 V. (2 p.)
- 0,75 V. (2 p.)
- 0,375 V. (2 p.)
- 1,5 V. (2 p.)
1.7 Välj rätt alternativ. 2 p.
- Friktionskraft är en vektorstorhet och friktionskoefficienten är en skalärstorhet. (2 p.)
1.8 Välj rätt alternativ. 2 p.
- Rörelseenergi är en skalärstorhet och rörelsemängd är en vektorstorhet. (2 p.)
1.9 Vid en atomkärnas alfasönderfall emitterar kärnan 2 p.
- en heliumkärna. (2 p.)
1.10 Vid parbildning 2 p.
- växelverkar en foton med en atomkärna varvid en elektron och en positron uppstår. (2 p.)
Del 2: 15-poängsuppgifter
2. Häcklöpning 15 p.
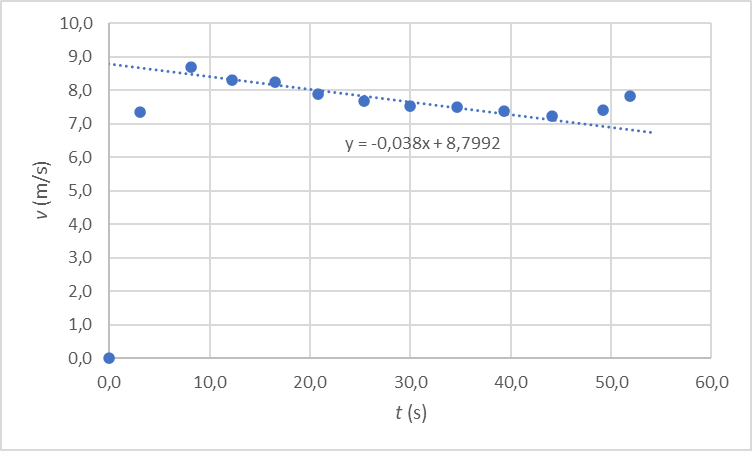
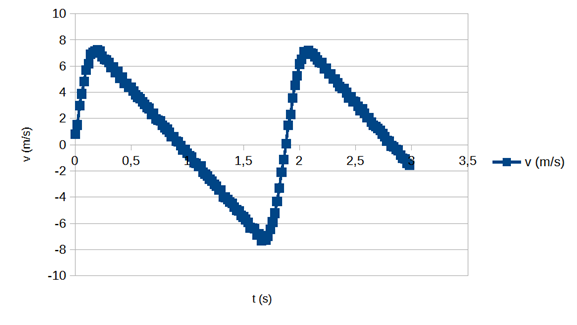
2.1 Gör en grafisk presentation av McLaughlins fart som funktion av tiden. I mitten av loppet kan man notera att farten ändras jämnt. Bestäm storleken av accelerationen under tidsintervallet 8,0–45 s. 7 p.
En linjär anpassning till det efterfrågade området ger McLaughlins acceleration som a = −0,03796 m/s2 ≈ −0,038 m/s2. McLaughlins fart minskade alltså med ungefär 0,038 m/s2 i sträckans mellanskede.
Poängsättning:
Det har presenterats en graf där de uppmätta värdena för McLaughlins fart som funktion av tiden syns som enskilda mätpunkter. (3 p.)
-
Om mätpunkterna inte syns eller om de saknas är avdraget två poäng.
-
Om endera axelns siffervärden är felaktiga eller saknas är avdraget två poäng.
-
Om två olika anpassningar, eller en anpassning och en bruten linje, syns i grafen är avdraget en poäng.
-
Om storhetens beteckning eller enhet saknas från endera axeln, eller om axlarna är omvända, är avdraget för varje fel en poäng.
En linjär anpassning har visats i en grafisk presentation och riktningskoefficienten för anpassningen har använts. (2p.)
Som svar har med 2 – 3 gällande siffrors noggrannhet givits en acceleration vars absolutbelopp är inom intervallet 0,037 \rm m/s^2 - 0,039 \rm m/s^2. (2 p.)
Typiska fel:
-
Endast en bruten linje har visats i grafen, i vilket fall de enskilda mätpunkterna inte syns.
-
Medelhastigheten har bestämts med hjälp av två \left(v{,}t\right) -punkter.
2.2 I mitten av loppet kunde McLaughlin ta in på Muhammads försprång. Bestäm med hjälp av den grafiska presentationen sträckan som vardera löparen sprang under tidsintervallet 0–26 s. Vem ledde efter att loppet hade pågått i 26 sekunder? 5 p.
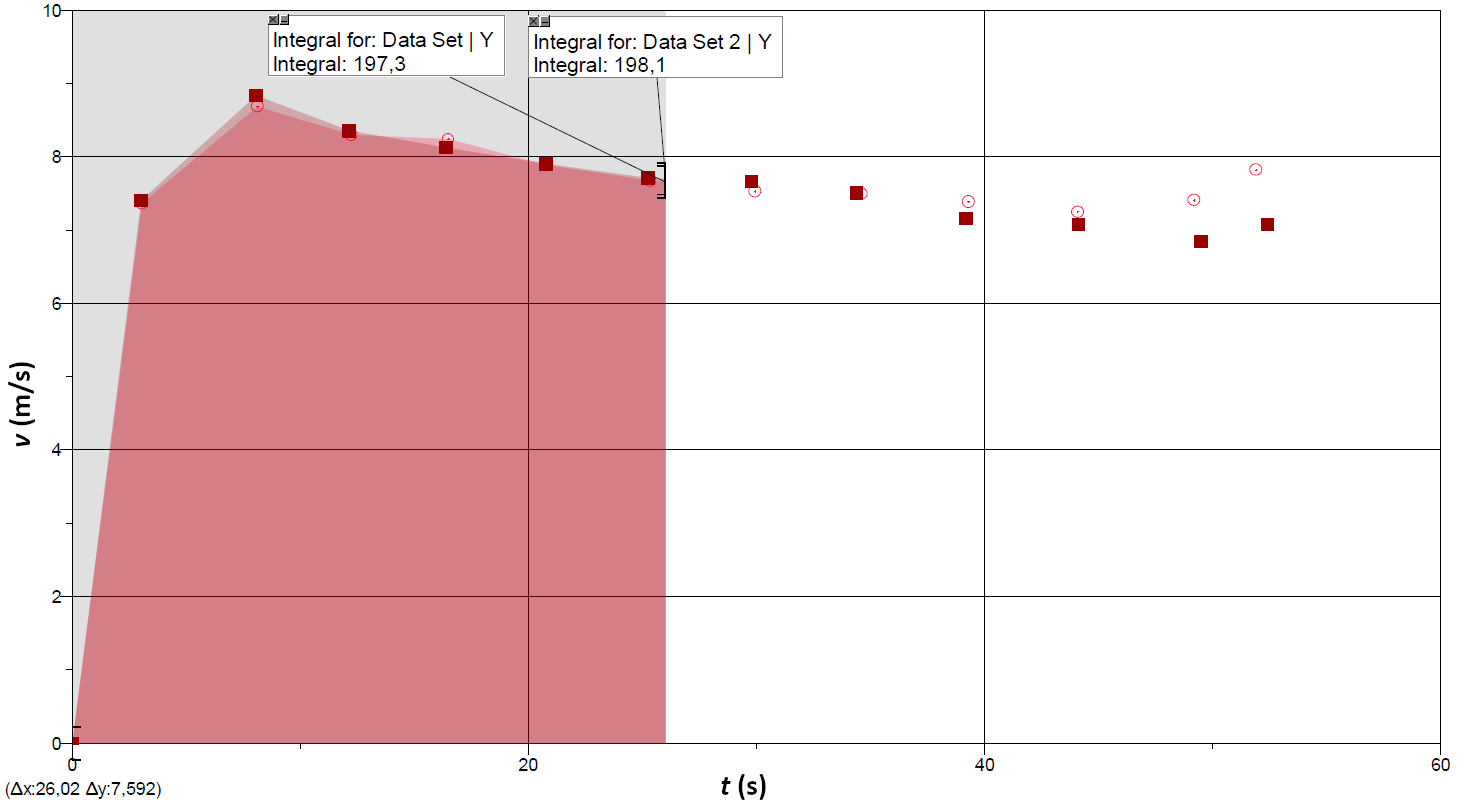
Genom grafisk eller numerisk integration är det möjligt att bestämma sträckan som båda löparna färdats vid en viss tidpunkt. Farten för Muhammad vid varje tidpunkt läggs till samma graf som McLaughlins fart, varvid följande graf och integral erhålls:
Från integralen ser vi att McLaughlin på 26 sekunder hade löpt sträckan 197,3 m, medan Muhammad hade löpt sträckan 198,1 m på samma tid.
Därmed var Muhammads ledning x = 198,1 m – 197,3 m = 0,8 m, när loppet hade pågått i 26 s.
Poängsättning:
Det har presenterats en graf och berättats att ytan under kurvan i grafen motsvarar den löpta sträckan. (2 p.)
Som svar har på korrekt sätt beräknats och med 3 – 4 gällande siffrors noggrannhet givits sträckorna som båda löparna har färdats. Sträckorna ska vara ungefär 200 m och sträckan som Muhammad har färdats ska vara en aning längre. (2 p.)
Det har svarats att Muhammad leder. (1 p.)
Typiska fel: Sträckan som färdats har beräknats genom att sinsemellan multiplicera hastighets- och tidskolumnerna, alldeles som om hastigheten skulle ha varit konstant.
2.3 Efter en hur lång löpsträcka passerade McLaughlin Muhammad? 3 p.
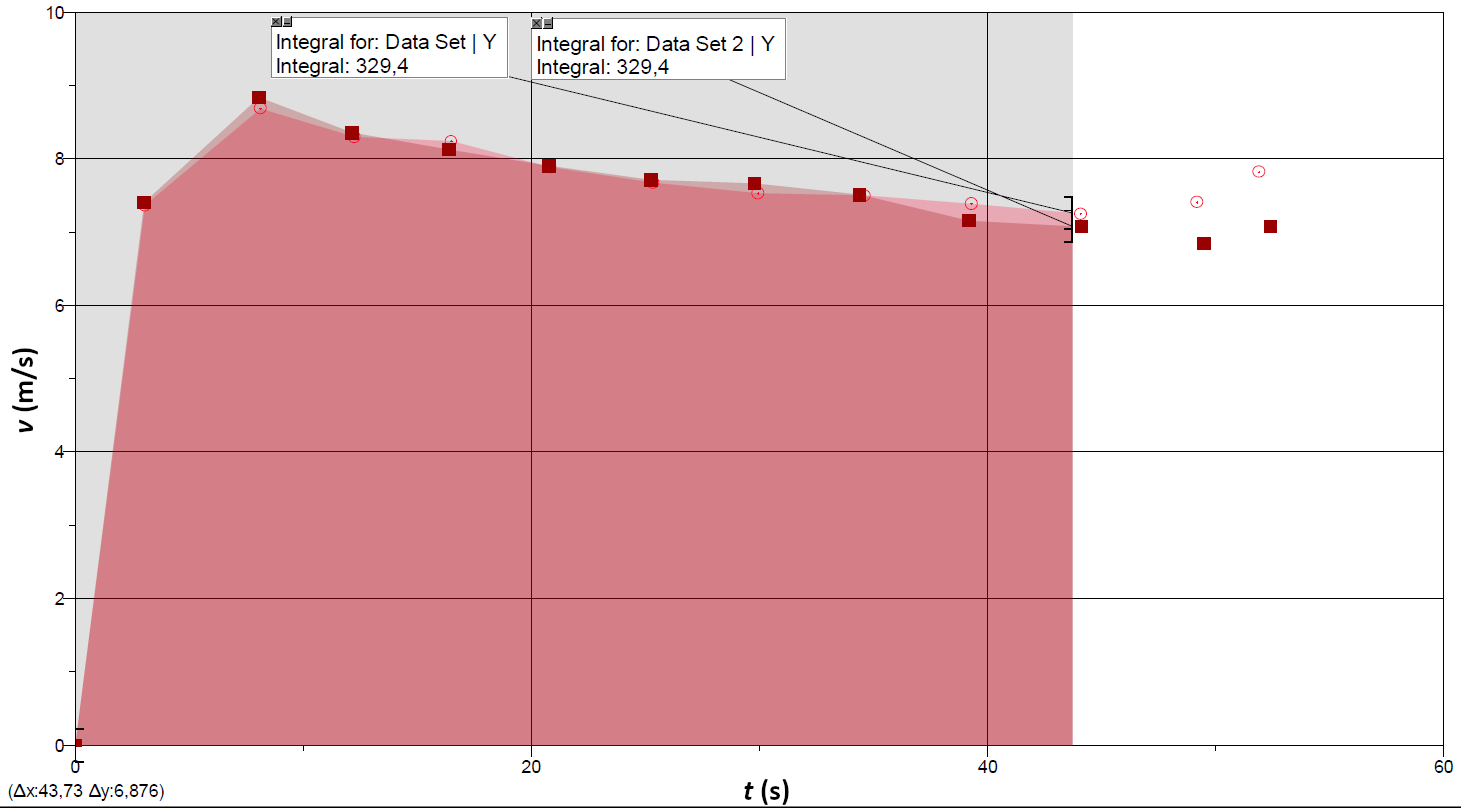
Genom grafisk eller numerisk integrering är det möjligt att jämföra sträckorna som båda löparna har löpt på samma tid också vid senare tidpunkter.
Genom att jämföra areorna under båda kurvorna märker vi att båda löparna hade löpt en lika lång sträcka på samma tid när ungefär 329 meter av den totala sträckan var bakom dem. (3 p.) Vid tidigare tidpunkter hade Muhammad löpt en längre sträcka, emedan McLaughlin var i en klar ledning vid senare tidpunkter. Därmed passerade McLaughlin Muhammadin när x = 329 m av den totala sträckan hade löpts.
Poängsättning: Med hjälp av grafisk eller numerisk integrering har rätt sträcka beräknats med 2 – 4 gällande siffrors noggrannhet inom intervallet 320 \rm{m} - 340 \rm{m} (3 p).
Typiska fel:
-
Sträckan som färdats har beräknats genom att sinsemellan multiplicera hastighets- och tidskolumnerna, alldeles som om hastigheten skulle ha varit konstant.
-
Tidpunkten för passeringen har givits i stället för sträckan.
3. En luftvärmepump 15 p.
En varm sommardag kyls ett hus ner med en luftvärmepump som överför värme inifrån huset till luften utanför. Tack vare kylningen är temperaturen inne i huset 21 ˚C då utomhusluftens temperatur är 25 ˚C. Värmefaktorn för luftvärmepumpen som kyler huset är 3,2. Luftvärmepumpen förbrukar 1,6 kWh elektrisk energi under en timmes tid.
Luftvärmepumpen har en inomhusenhet och en utomhusenhet. Utomhusenheten som är fäst på husets yttervägg utför arbetet för att överföra värme från insidan till utsidan av huset. Luftvärmepumpens energiflöden visas i bild . Luftvärmepumpens värmefaktor vid kylning är förhållandet mellan den energi som överförts från huset i form av värme och den elektriska energi som krävs för pumpen.
3.1 Hur mycket värme (i enheten kWh) överförs från huset på en timme? 5 p.
Värmefaktorn \varepsilon är enligt definitionen förhållandet mellan värmet som överförs från huset och arbetet som värmepumpen utför
\varepsilon=\frac{Q_0}{W},
alltså är Q_0=\varepsilon W = 3{,}2 \cdot 1{,}6 \rm{ kWh} = 5,12 kWh ≈ 5,1 kWh.
Poängsättning:
Det har presenterats en korrekt löst storhetsekvation för värmet. (2 p.)
Ett till absolutbeloppet korrekt svar har givits med 2 – 3 gällande siffrors noggrannhet. (3 p.)
Typiska fel:
-
En löst storhetsekvation saknas.
-
Den givna bilden av luftvärmepumpens energiflödesschema har inte utnyttjats.
3.2 Hur mycket värme (i enheten kWh) överförs till utomhusluften på en timme? 5 p.
Enligt termodynamikens första huvudsats är värmet som överförs från huset till luften utanför
Q_1=W+Q_0,
alltså är Q_1 = W + \varepsilon W = 1,6 kWh + 5,12 kWh = 6,72 kWh ≈ 6,7 kWh.
Poängsättning:
En motivering för värmemängden som överförs till luften utanför huset har givits med hjälp av termodynamikens första huvudsats, energins bevarande eller bilden i materialet. ( 2p.)
Det har presenterats en korrekt löst storhetsekvation för värmet. (2 p.)
Ett till absolutbeloppet korrekt svar har givits med 2 – 3 gällande siffrors noggrannhet. (1 p.)
Typiska fel:
-
Skillnaden mellan värmet som avges från huset och värmet som mottas av luften utanför har inte identifierats.
-
Som svar har givits 3,5 kWh.
3.3 Utomhusluftens temperatur stiger till 32 ˚C. Hur stor måste värmepumpens elektriska effekt vara om man fortfarande vill hålla husets inomhustemperatur vid 21 ˚C? Du kan anta att luftvärmepumpens värmefaktor inte är beroende av temperaturen. Du kan också anta att värme överförs från utomhusluften till huset endast genom ledning och att effekten för ledningen är proportionell mot temperaturskillnaden. 5 p.
Pumpen måste överföra värme från huset med lika stor effekt som värme leds in utifrån för att inomhustemperaturen inte ska stiga. Effekten för värmeledningen mellan huset och utomhusluften är direkt proportionell mot temperaturskillnaden P=UA\Delta T , där U är värmeöverföringskoefficienten och A är arean för ledningen. Då temperaturskillnaden \Delta T stiger från 4 ⁰C till 11 ⁰C ökar behovet att överföra värme från huset i samma förhållande som temperaturskillnaderna. Den elektriska effekten som behövs för det här ökar i samma förhållande, alltså:
P_{\rm ny}=P\frac{\Delta T_{\rm ny}}{\Delta T}=1,6\,{\rm kW}\,\frac{11\, ^\circ{\rm C}}{4\, ^\circ{\rm C}}=4,4\,{\rm kW}.
Poängsättning:
För den efterfrågade effekten eller arbetet som utförs på en timme har det lösts och presenterats en storhetsekvation där det korrekta beroende av temperaturskillnaderna framgår. (2 p.)
Ett till absolutbeloppet korrekt svar för effekten har givits med 2 – 3 gällande siffrors noggrannhet. (3 p.)
Typiska fel: Uppgiften har lösts utan storhetsekvationer.
4. Ett jordskred 15 p.
4.1 Bestäm stenblockets acceleration. 8 p.
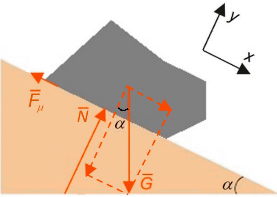
Stenblockets massa är m=2200\,{\rm kg} och sluttningens lutningsvinkel är \alpha=28^\circ. Stenblockets acceleration är a. Tyngdkraften som påverkar blocket är \bar G, ytans stödkraft \bar N och friktionskraften \bar F_\mu. Vi skriver Newtons andra lag i komponentform:
x-riktning:
ma=G\sin\alpha-F_\mu
y-riktning:
N-G\cos\alpha=0.
Tyngdkraften är G=mg, där g=9,81\,{\rm m/s}^2 är tyngdaccelerationen. Glidfriktionen beskrivs med en enkel friktionskoefficientmodell, F_\mu=\mu N, där \mu=0,40 är glidfriktionskoefficienten mellan blocket och sluttningen. Eftersom y-riktningens rörelseekvation ger oss N=G\cos\alpha=mg\cos\alpha, får vi som friktionskraft F_\mu=\mu mg\cos\alpha. Från x-riktningens rörelseekvation kan vi nu bestämma stenblockets acceleration:
a=g(\sin\alpha-\mu\cos\alpha)=1,141\,{\rm m/s}^2\approx 1,1\,{\rm m/s}^2.
Poängsättning:
För stenblocket har det presenterats en kraftfigur där det endast syns tre kraftvektorer som har rätt riktning och är namngivna. (2 p.)
-
En liten kraftvektor som korrekt beskriver luftmotståndet tillåts.
-
Ifall att en kraftvektor inte är fast i blocket eller om övriga kraftvektorer har ritats fast i stenblocket ger kraftfiguren 0 p.
-
Ifall att krafterna inte har namngivits eller att namngivningen inte är entydig ger kraftfiguren 0 p.
Det har presenterats en korrekt rörelseekvation för stenblocket i sluttningens riktning i formen ma=G_{\rm x} \ldots, ma = G \sin{\alpha} \ldots eller ma = mg \sin{\alpha} \ldots (2 p.)
Det har presenterats en korrekt rörelseekvation eller jämviktsekvation i riktningen vinkelrät mot sluttningen. (2 p.)
Rörelseekvationerna kan även skrivas med hjälp av vektorer.
En korrekt storhetsekvation löst för accelerationen har givits tillsammans med rätt värde för accelerationen med 2 – 3 gällande siffrors noggrannhet. (2 p.)
Typiska fel:
-
En pil som beskriver hastighet eller acceleration ritas fast i kroppen.
-
Fel trigonometriska funktioner används för att dela upp krafterna i komponenter.
-
Rörelseekvationerna har skrivits fel med hjälp av vektorer, exempelvis m \vec{a} = \vec{G}_{\rm x} - \vec{F}_{\mu} eller ma = \vec{G}_{\rm x} + \vec{F}_{\mu}.
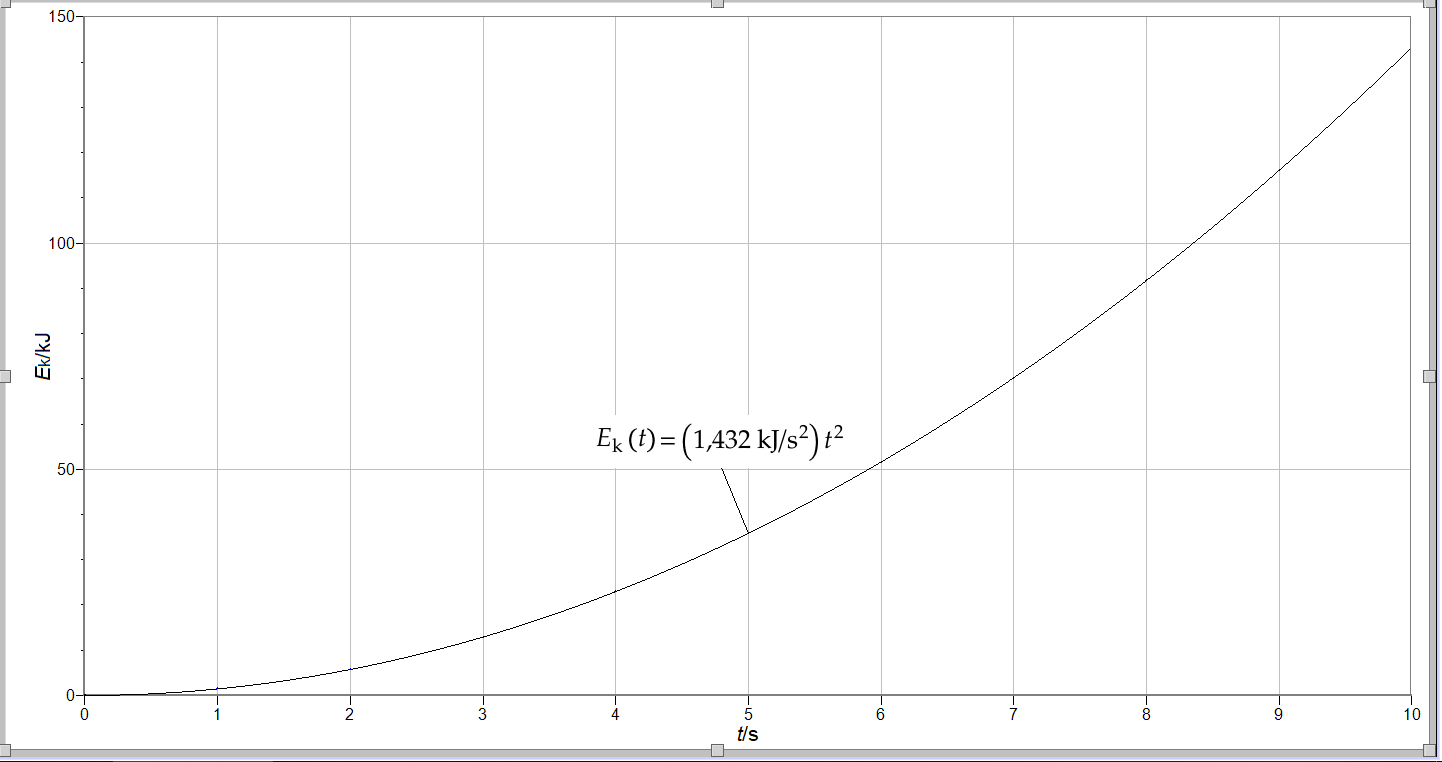
4.2 Härled ett uttryck för stenblockets rörelseenergi som funktion av tiden. Gör med hjälp av uttrycket du härlett en grafisk presentation av rörelseenergin som funktion av tiden inom intervallet 0–10 s. 7 p.
Stenblockets rörelse är likformigt accelererad. Blockets hastighet är alltså v(t)=v_0+at, där begynnelsehastigheten är v_0=0. Som stenblockets rörelseenergi får vi E_k(t)=\tfrac{1}{2}m[v(t)]^2=\tfrac{1}{2}m(at)^2=\tfrac{1}{2}ma^2t^2=(1432\,{\rm kg\,m}^2/{\rm s}^4)t^2=({\rm 1,432}\,{\rm kJ/s}^2)t^2.
Graf:
Poängsättning:
Rörelseenergins storhetsekvation har presenterats med hjälp av tiden och acceleration, antingen med storhetssymboler eller med de korrekta värdena med enheter. (2 p.)
Det har presenterats en graf över rörelseenergin som funktion av tiden. Ett korrekt värde för rörelseenergin ska kunna avläsas för varje tidpunkt. Grafen bör motsvara det härledda uttrycket. (5 p.)
-
Om funktionen är något annat än en parabel ges inga poäng för grafen.
-
Om det saknas en heldragen linje som beskriver funktionen eller om den syns som en alltför grov bruten linje är avdraget tre poäng.
-
Om grafen är ritad som funktion av tidens kvadrat är avdraget tre poäng.
-
Om en axels siffervärden är felaktiga eller saknas är avdraget två poäng.
-
Om den presenterade grafen är ritad för något annat än det efterfrågade tidsintervallet är avdraget två poäng.
-
Om värdena för en storhet eller storhetens beteckning saknas eller är felaktiga är avdraget två poäng.
-
Om storhetens enhet saknas eller om axlarna är omvända är avdraget för vardera fel en poäng.
Typiska fel:
-
Ett fel görs i rörelseenergins storhetsekvation eller i dess enheter, eller den lämnas oskriven med hjälp accelerationen och tiden.
-
Grafen ritas med en negativ tid.
5. Mars och dess månar 15 p.
5.1 Beräkna storleken av kraften mellan Phobos och Deimos då de befinner sig som närmast varandra. Beräkna också storleken av kraften mellan planeten Mars och Deimos. Vad är förhållandet mellan de här krafternas storlek? 6 p.
Det kortaste avståndet mellan Phobos och Deimos är R = rD – rP, där rD är radien för Deimos omloppsbana och rP är radien för Phobos omloppsbana. På det här avståndet attraherar de varandra med kraften G_{\rm DP}=\gamma m_{\rm D}m_{\rm P}/R^2, då m_\rm P = 1,08 \cdot 10^{16} \rm{kg} och m_\rm D = 1,80 \cdot 10^{15} \rm{kg} är massorna för Phobos och Deimos.
Mars och Deimos är konstant på avståndet rD från varandra och attraherar varandra med kraften G_{\rm DM}=\gamma m_{\rm D}m_{\rm M}/r_{\rm D}^2, då m_\rm M = 6{,}417 \cdot 10^{23} \rm{kg} är Mars massa.
Genom att substituera värdena från material 5.A och gravitationskonstanten (\gamma = 6,67428\cdot 10^{-11}\,{\rm Nm}^2/{\rm kg}^2) får vi värdena G_{\rm DP}=6,539\cdot 10^{6}\,{\rm N} och G_{\rm DM}=1,400\cdot 10^{14}\,{\rm N}. Som förhållande mellan krafterna får vi G_{\rm DM}/G_{\rm DP}=2,14\cdot 10^7 eller dess invers 4,67\cdot 10^{-8}.
Poängsättning:
En storhetsekvation för gravitationskraften har presenterats och använts i lösningen. (2 p.)
Korrekt svar för kraften mellan Phobos och Deimos har givits med 2 – 3 gällande siffrors noggrannhet. (2 p.)
Korrekt svar för kraften mellan Mars och Deimos har givits med 2 – 3 gällande siffrors noggrannhet. (1 p. )
Korrekt svar för förhållandet mellan krafterna har givits med 2 – 3 gällande siffrors noggrannhet. (1 p.)
Typiskt fel: Det har inte märkts att massorna för Phobos och Deimos endast har givits med tre gällande siffrors noggrannhet och det har använts för många gällande siffror i svaren.
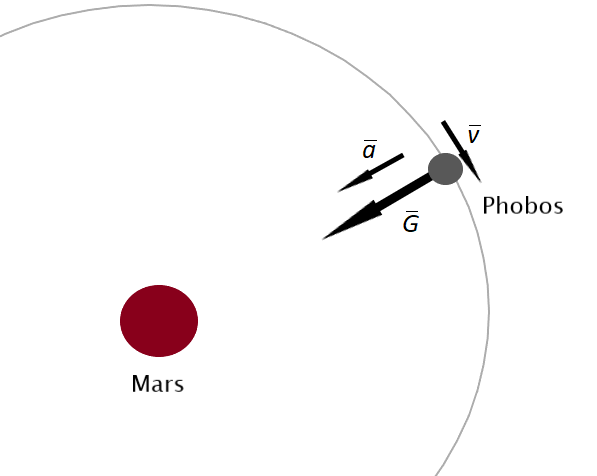
5.2 Rita en kraftfigur för Phobos och bestäm massan för Mars utgående från egenskaperna för Phobos omloppsbana. Bestäm sedan Mars massa utgående från egenskaperna för Deimos omloppsbana. Hur noggrant kan du ange Mars massa utgående från dina resultat? 9 p.
Phobos påverkas endast av gravitationskraften G förorsakade av Mars. Gravitationskraften GDP förorsakad av Deimos är försvinnande liten enligt deluppgift 5.1 och dess riktning ändras hela tiden då månarna kretsar kring Mars.
Mars och Phobos attraherar varandra med kraften G_{\rm PM}=\gamma m_{\rm P}m_{\rm M}/r_{\rm P}^2.
Den här kraften orsakar en centripetalacceleration an för Phobos, eftersom det är den enda kraften som påverkar Phobos. Enligt Newtons II lag är G_{\rm PM}=m_{\rm P}a_n.
Å andra sidan får vi centripetalaccelerationen för en cirkelrörelse ur ekvationen a_n=v^2/r_{\rm P}.
Omloppstiden TP är konstant, alltså är banhastigheten v = 2 \pi r_{\rm P} / T_{\rm P} konstant och som centripetalacceleration får vi a= 4 \pi^2 r_{\rm P} /T_{\rm P}^2 . Genom att med hjälp av det här skriva rörelseekvationen i formen m_{\rm P} 4 \pi^2 r_{\rm P} /T_{\rm P}^2 =\gamma m_{\rm P}m_{\rm M}/r_{\rm P}^2 kan vi för Mars massa lösa ut ekvationen m_{\rm M}=4\pi^2 r_{\rm P}^3/(\gamma T_{\rm P}^2). Genom att substituera med siffervärdena kan vi uppskatta Mars massa till värdet m_{\rm M}=6,4205\cdot 10^{23}\,{\rm kg.}
Om vi gör motsvarande beräkning med Deimos banradie och omloppstid får vi för Mars massa storhetsekvationen m_{\rm M}=4\pi^2 r_{\rm D}^3/(\gamma T_{\rm D}^2) och ett värde för massan m_{\rm M}=6,4163\cdot 10^{23}\,{\rm kg.}
Vi kan se att de två erhållna uppskattningarna motsvarar varandra med tre siffrors noggrannhet, alltså kan vi ange Mars massa som m_{\mathrm{M}}=6{,}42\cdot10^{23}\ \mathrm{kg}. Värdet stämmer överens med materialet och MAOL:s tabeller.
Poängsättning :
Det har presenterats en kraftfigur i vilken endast en kraftvektor namngiven som gravitation är ritad från Phobos i riktning mot Mars. (2 p.)
-
Om kraftvektorn inte rör i Phobos, eller om andra krafter har ritats fast i Phobos, ges inga poäng för kraftfiguren.
-
Om det inte framgår ur kraftfiguren i vilken riktning banans mittpunkt eller Mars befinner sig ges inga poäng för kraftfiguren.
Lösningen har motiverats genom att omnämna Newtons II lag och skriva en rörelseekvation i enlighet med den genom att använda en gravitationskraft. (2 p).
Det har presenterats en korrekt storhetsekvation för Phobos banhastighet. (1 p.)
Det har presenterats en storhetsekvation för Mars massa och utgående från den har Mars massa beräknats. (2 p.)
Det har svarats på frågan om ”Hur noggrant” antingen genom att meddela de gällande siffrornas antal eller med ett massintervall. (2 p.)
Typiska fel:
-
En kraftvektor som beskriver hastighet eller acceleration ritas fast i Phobos.
-
En jämförelse görs endast till litteraturvärdet för Mars massa.
6. I enlighet med Millikans experiment 15 p.
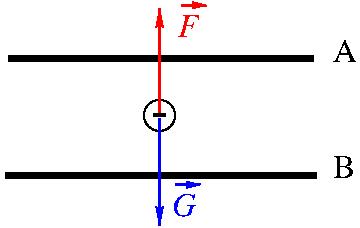
6.1 Rita droppens kraftfigur. Vilken skiva, A eller B, är negativ laddad? Motivera ditt svar. 5 p.
Droppen är i jämvikt. Tyngden \overrightarrow{G} är riktad neråt. Den elektriska kraften \overrightarrow{F} måste alltså vara riktad uppåt. Eftersom droppen är negativt laddad måste den nedre skivan B vara negativ och den övre skivan positiv för att den elektriska kraften som påverkar droppen ska riktas uppåt.
Svar: B
Poängsättning:
Det har presenterats en kraftfigur i vilken två namngivna kraftvektorer har ritats i de korrekta riktningarna från droppen. (2 p.)
-
Den elektriska kraften kan även beskrivas med kraften förorsakad av vardera skivan om det förklaras i texten.
-
Om kraftvektorn inte är fast i droppen eller om andra pilar har ritats fast i droppen ges inga poäng för kraftfiguren.
-
Om det i kraftfiguren har ritats en pil som beskriver hastighet eller acceleration ges inga poäng för kraftfiguren.
-
Om kraftvektorerna är klart av olika längd är avdraget en poäng.
Som rätt svar har getts skiva B (1 p.) och svaret har motiverats korrekt. (2 p.).
Typiska fel:
-
Kraftpilarna som ritats på droppen resulterar inte i ett jämviktstillstånd.
-
Endast växelverkan mellan den ena av skivorna och droppen har undersökts.
-
Det har inte nämnts att kraften som verkar uppåt är en elektrisk kraft.
6.2 Hur många överloppselektroner finns det i oljedroppen? 10 p.
Droppen har formen av ett klot, alltså är dess massa m=\tfrac{4}{3}\pi r^3\rho, där r är droppens radie och ρ är dess densitet. Droppens tyngd är därmed \vec G=m\vec g=\tfrac{4}{3}\pi r^3\rho\vec g.
Eftersom droppen har en laddning påverkas den av en elektrisk kraft \vec F=q\vec E, där q är droppens nettoladdning och E är styrkan av det elektriska fältet som är riktat neråt.
Då droppen svävar är krafterna lika stora, \vec F+\vec G=0.
För det elektriska fältet mellan kondensatorskivorna gäller E= \frac{U}{d} , där U är spänningen och d är avståndet mellan skivorna.
Vid jämviktsläge är tyngdkraften och den elektriska kraften lika stora och riktade mot varandra, alltså är\frac{qU}{d}=\frac{4}{3}\pi r^3\rho g. Vi löser för laddningen: q=\frac{4d\pi r^3\rho g}{3U}.
Genom att substituera med siffervärdena får vi absolutbeloppet av laddningen │q│= 1,631057 · 10-18 C.
Enligt den tidigare deluppgiften är droppen negativt laddad, alltså är q = -1,631057 · 10-18 C. Förhållandet mellan droppens laddning och laddningen hos en elektron är \frac{q}{-e}\approx10{,}18.
Vi avrundar till närmaste heltal, eftersom laddningen måste vara en heltalsmultipel av enhetsladdningen e=1{,}60\cdot10^{-19} \rm C .
Svar: 10 elektroner.
Poängsättning:
Det har presenterats en korrekt jämvikts- eller rörelseekvation för droppen. (2 p.)
En storhetsekvation för droppens massa har presenterats med hjälp av densiteten, eller så har massan eller tyngden bestämts korrekt. (2 p.)
En storhetsekvation för den elektriska kraften har presenterats med hjälp av potentialskillnaden och avståndet mellan skivorna. (2 p.)
Det har presenterats en korrekt storhetsekvation för droppens laddning eller för antalet elektroner på droppen. (2 p.)
Rätt svar har givits som ett heltal. (2 p.)
Typiska fel: Svaret ges som decimaltal.
7. Ett elektroniskt lås 15 p.
Ett elektroniskt lås på en dörr öppnas genom att man för en nyckelbricka nära en avläsare (bild ). Avläsaren skapar ett magnetiskt fält runt sig, inom vilket nyckelbrickan aktiveras. Om det är rätt bricka öppnar avläsaren låset.
I stället för nyckelbrickan placerades en spole på avläsaren. Mellan spolens poler kopplades ett motstånd vars resistans var 330 Ω i enlighet med bild . Mellan motståndets poler kunde man då med hjälp av ett oscilloskop mäta en högfrekvent sinusformad växelspänning med amplituden 1,2 V. Spolens egen resistans var liten och spolen rörde sig inte under mätningen.
7.1 Förklara hur spänningen mellan motståndets poler uppstår. 4 p.
Avläsaren skapar ett magnetfält som varierar med tiden. Det magnetiska flödet som går genom spolen varierar med tiden, och enligt induktionslagen induceras då i spolen en spänning som kan observeras mellan motståndets poler.
Poängsättning:
Det har identifierats att avläsaren skapar ett föränderligt magnetfält. (2 p.)
Det har berättats att spänningen mellan motståndets poler orsakas av spänningen som induceras i spolen. (2 p.)
Typiskt fel: Det har påståtts att det induceras en elektrisk ström i spolen som sedan orsakar en spänning. Det här svaret ger inga poäng för skapande av spänningen.
7.2 Motståndet som var kopplat till spolen byttes ut mot ett annat motstånd med resistansen 1,0 kΩ. Hur stor var amplituden för växelspänningen mellan det här motståndets poler? Motivera ditt svar. 4 p.
Enligt induktionslagen är den inducerade spänningen endast beroende av spolens och fältets egenskaper. Spänningens amplitud ändras inte, utan den är fortfarande 1,2 V.
Poängsättning: Det har med motiveringar berättats att spänningen endast beror på fältet och spolens egenskaper (2 p.) och att spänningen hålls oförändrad på grund av det. (2 p.)
Typiska fel: Det har tänkts att strömmen som induceras i spolen hålls konstant och att spänningen då växer till 3,6 V.
7.3 Spolen flyttades längre bort från avläsaren. Varför minskade amplituden på den uppmätta spänningen? 4 p.
Den magnetiska flödestätheten är mindre på längre avstånd från avläsaren. Då är även det magnetiska flödet som går genom spolen mindre, och därför är dess förändringshastighet också mindre. I enlighet med induktionslagen är den inducerade spänningen mindre.
Poängsättning: Det har omnämnts att den magnetiska flödestätheten minskar då avståndet från avläsaren ökar (2 p.) och att en följd av det här är att förändringarna i det magnetiska flödet som passerar genom spolen då är mindre och skapar en mindre induktionsspänning. (2 p.)
Typiska fel:
-
Det påstås att spolens position påverkar hur stort fält som avläsaren skapar.
-
Det påstås att den magnetiska flödestätheten som avläsaren skapar följer storhetsekvationen för den magnetiska flödestätheten från en rak ledare B = \mu_o I / 2 \pi r. Det verkliga avståndsberoendet är inte så här enkelt. Inga poäng dras av för felet om de eftersökta sakerna är korrekt beskrivna.
7.4 I bilderna presenteras sex möjliga grafer för den magnetiska flödestätheten B (tjock heldragen linje). I varje graf har också spänningen V mellan motståndets poler ritats (streckad linje) för att underlätta jämförelsen. Vilken av graferna motsvarar bäst den magnetiska flödestätheten som funktion av tiden vid spolens läge? 3 p.
-
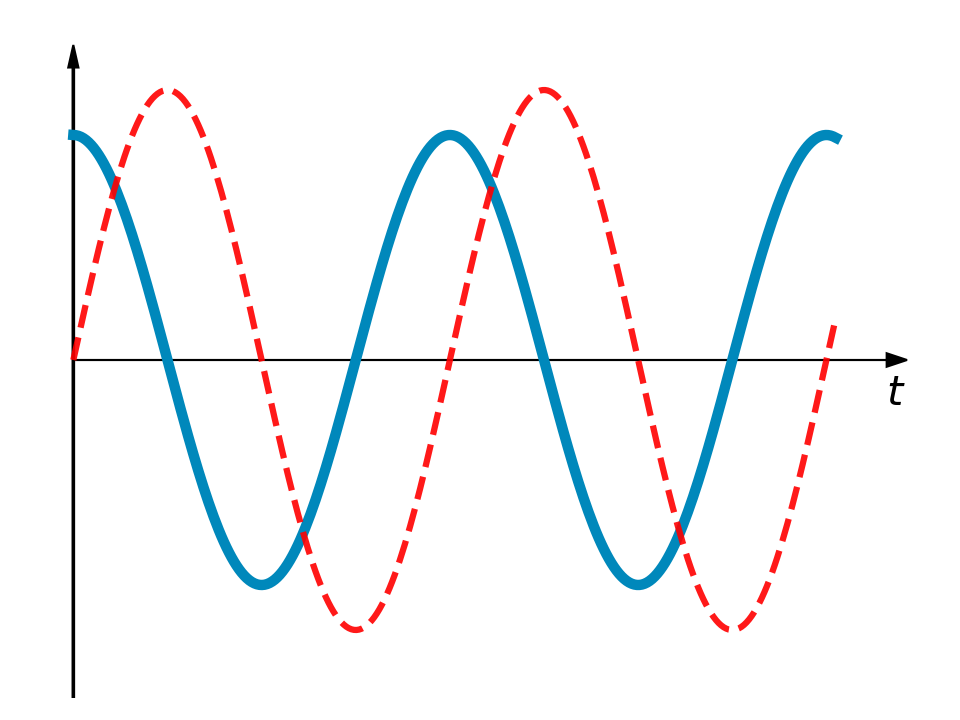 (3 p.)
(3 p.)
8. Kärnreaktioner i det tidiga universum 15 p.
8.1 Beräkna hur stor neutronernas andel var av nukleonerna (R) då universums temperatur var T=1,0\cdot 10^{10}\,{\rm K}. 5 p.
I uppgiften behövs följande information
m_{\rm n}=1,67492747\cdot 10^{-27}\,{\rm kg} m_{\rm p}=1,67261898\cdot 10^{-27}\,{\rm kg} c=3,0\cdot 10^8\,{\rm m/s} k=1,380649\cdot 10^{-23}\,{\rm J/K} T=1,0\cdot 10^{10}\,{\rm K}
och dessutom skillnaden mellan neutronens och protonens massor
\Delta m=m_{\rm n}-m_{\rm p}>0.
Vi använder ekvationen i materialet
\frac{N_{\rm n}}{N_{\rm p}}=\exp\Bigl[-\frac{(m_{\rm n}-m_{\rm p})c^2}{kT}\Bigr]=0,2225\approx 0,22.
Ur dessa får vi
R=\frac{N_{\rm n}}{N_{\rm n}+N_{\rm p}}=\frac{\frac{N_{\rm n}}{N_{\rm p}}}{\frac{N_{\rm n}}{N_{\rm p}}+1}=0,1820\approx 0,18.
Poängsättning:
Korrekt svar har givits med två eller tre gällande siffrors noggrannhet. (5 p.)
Ifall att slutresultatet är inkorrekt ger rätt värde för neutronernas och protonernas förhållande två poäng.
Typiska fel: Som svar har det givits neutronernas och protonernas förhållande eller protonernas andel av nukleonerna.
8.2 Skriv en reaktionslikhet för en reaktion där en neutron omvandlas till en proton. 2 p.
Den efterfrågade reaktionen är {\rm n}+\nu_{\rm e}\to {\rm p}+{\rm e} eller {\rm n}\to {\rm p}+{\rm e}+\bar\nu_{\rm e}.
Poängsättning:
Endera av de korrekta reaktionslikheterna har skrivits. (2 p.)
-
Neutrinon får saknas eller förväxlas med dess antipartikel.
-
Protonen kan betecknas med symbolen för väte.
Typiska fel: Vätekärnan har betecknats med något felaktigt masstal.
8.3 Skriv en reaktionskedja där en helium-4 kärna slutligen uppstår från protoner och neutroner. Kedjan ska vara sådan att det på vänster sida av varje reaktionslikhet endast finns två partiklar eller kärnor. 3 p.
Produktion av helium-4 lyckas exempelvis på följande sätt: först produceras två deuteroner med två reaktioner {\rm p}+{\rm n}\to {\rm D}, och sedan produceras en heliumkärna ur dem med reaktionen \mathrm{D}+\mathrm{D\ }\rightarrow\ ^4\mathrm{He}.
Poängsättning:
Det har korrekt skrivits den första reaktionslikheten (1 p.) och de övriga nödvändiga reaktionslikheterna (1 p.) samt meddelats ifall det för någon av reaktionerna behövs fler än en. (1 p.)
-
Ifall att den första reaktionslikheten är fel kan inga poäng fås för deluppgiften.
-
Ifall att det på reaktionslikhetens vänstra sida finns en eller flera än två partiklar ges inga poäng för reaktionslikheten.
-
Även andra reaktionskedjor än den ovan nämnda som utgår ifrån protoner och neutroner och producerar en \rm{^4He}-kärna ger poäng för korrekt svar.
Typiska fel: Vätekärnan har betecknats med något felaktigt masstal.
8.4 Studera bilden i material . Vad kan man utgående från bilden konstatera om den teoretiska modellen den presenterar i jämförelse med observationerna? Gör en grov bedömning av förhållandet mellan massandelarna för helium och väte vid positionen för observationerna i bilden. 5 p.
Grafen i materialet visar de lätta kärnornas massandelar S som funktion av densiteten D. Vardera axeln är relativ. Den lodräta linjen och kurvornas skärningspunkter beskriver WMAP-satellitens observationer. Ur grafen kan vi se att den teoretiska modellen som utgår från teorin om ursmällen är bra på att förutspå de observerade relativa andelarna av de lätta isotoperna i rymden.
Ifall M_1 är vätets massandel och M_2 är heliums massandel så kan vi enligt bilden direkt avläsa från ^4He -kurvans skärningspunkt inversen till det efterfrågade förhållandet mellan massandelarna, eftersom massandelarna är normaliserade med väte-kärnornas massandel S_0. \frac{M_1}{M_2}\approx \frac{1}{0,2}=5.
Poängsättning:
Det har berättats att modellen är bra på att förutspå de lätta isotopernas andelar i rymden. (3 p.)
Som svar har det korrekta förhållandet mellan massandelarna givits med en eller två gällande siffrors noggrannhet. (2 p.)
Typiska fel: Från bilden har det förklarats om förändringen av isotopernas massandelar som funktion av tiden eller densiteten.
Del 3: 20-poängsuppgifter
9. En studsmatta 20 p.
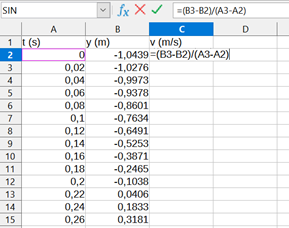
9.1 Förklara hur fysikerns hastighet kan beräknas utgående från tabell . Rita en graf som visar fysikerns hastighet vid alla tidpunkter i tabell . 6 p.
En mätning av positionen har gjorts vid jämna tidsintervall \Delta t=20\,{\rm ms}. Vi beräknar medelhastigheten v=\frac{\Delta y}{\Delta t} för varje tidsintervall. Alternativt kan positionsdata deriveras som funktion av tiden exempelvis med hjälp av LoggerPro-programmet.
Vi ritar det erhållna positionsdata som funktion av tiden.
Graf:
Poängsättning:
Det har berättats att hastigheten kan fås som medelhastigheten för varje tidsintervall eller genom att derivera positionen med hänsyn till tiden, eller en derivering av mätdata har visats antingen grafiskt eller i tabell. (2 p.)
Det har presenterats en graf över fysikerns hastighet som funktion av tiden. (4 p.)
-
Ifall att grafen inte visar den korrekta hastigheten ges inga poäng för grafen.
-
Ifall att storheternas symboler eller namn eller enheter saknas eller är felaktiga är avdraget en poäng.
Typiska fel:
-
En harmonisk funktion har anpassats till mätpunkterna.
-
Det har beräknats ett förhållande mellan positions- och tidskolumnerna \frac{v}{t} eller en produkt v\cdot t och det här har använts som hastighet.
9.2 Vilken rörelsemodell beskriver fysikerns rörelse vid tidpunkten t = 0,1\,{\rm s}? 1 p.
- harmonisk svängningsrörelse (1 p.)
9.3 Vilken rörelsemodell beskriver fysikerns rörelse vid tidpunkten t = 0,5\,{\rm s}? 1 p.
- likformigt accelererad rörelse (1 p.)
9.4 Vid vilken tidpunkt ändras typen av rörelse följande gång efter tidpunkten t = 0,5\,{\rm s}? 1 p.
- 1,7 s (1 p.)
9.5 Bestäm fysikerns största acceleration. 4 p.
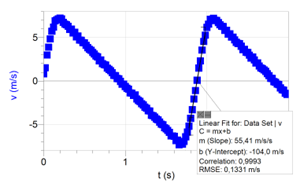
Fysikerns största acceleration har uppnåtts vid punkten där hastighetens lutningskoefficient är som störst. Accelerationen kan bestämmas från grafens tangent i den här punkten. Alternativt kan data deriveras på nytt som funktion av tiden och maximihastigheten kan avläsas ur den nya grafen. Fysikerns största acceleration är 55–58 m/s2.
Poängsättning:
Det har berättats att accelerationen kan erhållas genom att derivera hastigheten med hänsyn till tiden, eller en derivering av mätdata har visats grafiskt eller hastighetsgrafens tangent har använts. (2 p.)
Som svar har den korrekta accelerationen givits med två eller tre gällande siffrors noggrannhet inom intervallet 55 \rm{m/s^2} — 60 \rm{m/s^2} (2 p.)
Typiska fel:
-
Hastigheten har ritats som förhållandet mellan positions- och tidskolumnerna och ur detta har den största accelerationen sökts.
-
Positionen har ritats som funktion av tiden och riktningskoefficienten för en tangent i den grafen har använts som värdet på största accelerationen.
9.6 Härled ett uttryck för den största amplituden A vid vilken fysikerns fötter inte tappar kontakten med studsmattan. Använd text som hjälp. Vilken är den största möjliga amplituden vid vilken fötterna inte tappar kontakten med studsmattan om fysikerns massa är 68 kg och studsmattans "fjäderkonstant" är 4 600 N/m? 7 p.
Den största amplituden kan lösas med hjälp av antingen positionen eller krafterna. Enligt text 9.B är positionen vid en svängningsrörelse
y(t)=-\frac{mg}{k}-A\cos 2\pi ft.
Eftersom studsmattan inte påverkar hopparen med en kraft som är riktad neråt, kan positionen i en harmonisk rörelse som högst vara vid nivån för en obelastad studsmatta y=0. Därmed är
-\frac{mg}{k}-A\cos2\pi ft \leq 0.
Positionens största värde uppnås vid en sådan tidpunkt t då \cos\left(2\pi ft\right)=-1. Då blir -\frac{mg}{k}+A\ =\ 0, alltså får vi som amplitud
A=\frac{mg}{k}.
Alternativt kan vi konstatera att vid jämviktsläget gäller
\Sigma F=-ky_0-mg=0.
Därmed är jämviktsläget
y_0=-\frac{mg}{k}.
Hopparen tappar kontakten med studsmattan när \cos(2\pi f t)=-1 och då är fjäderkraften
F_j=-ky=0.
På grund av det här är den största möjliga amplituden lika med avståndet från jämviktsläget till den obelastade studsmattans nollnivå
A=|y_0|=\frac{mg}{k}.
Med den givna massan och värdet på "fjäderkonstanten" k får vi
A=\frac{68\,{\rm kg}\cdot 9,81\,{\rm m}/{{\rm s}^2}}{4600\,{\rm N/m}}=0,15\,{\rm m}.
Poängsättning:
Lösningen har motiverats på korrekt sätt med antingen en kraftundersökning eller svängningsrörelsen och jämviktspositionen. (3 p.)
En löst storhetsekvation för amplituden har skrivits (2 p.) och med två eller tre gällande siffrors noggrannhet har den korrekta amplituden givits inom intervallet 0,14 m – 0,15 m. (2 p.)
Typiska fel: Ur ekvationen för svängningsrörelsens position som givits i materialet har man löst för A och substituerat in värden som man på ett eller annat sätt kommit fram till.
10. En vattenflaska 20 p.
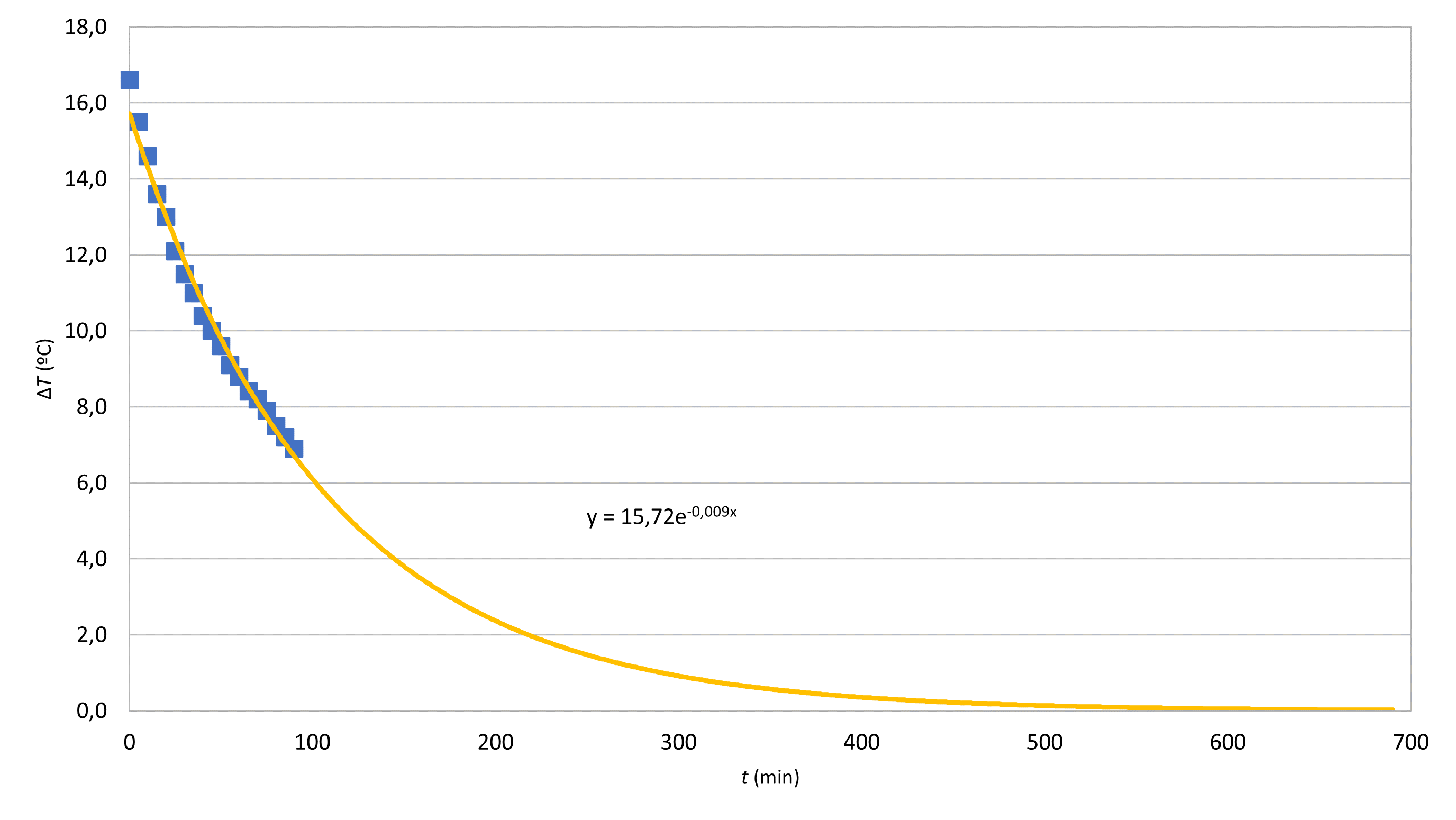
10.1 Gör en grafisk presentation som visar temperaturskillnaden mellan vattnet (tabell ) och rummet som funktion av tiden. Hur lång tid skulle det ta för vattentemperaturen att nå rumstemperaturen inom gränsen för mätnoggrannheten? 7 p.
Genom extrapolering (eller från den anpassade funktionen) kan vi konstatera att den anpassade funktionen minskar till mindre än 0,05 °C efter ungefär 580–610 minuter. Temperaturskillnaden uppnår alltså noll med termometerns noggrannhet på 0,1 °C efter ungefär 580–610 minuter.
Poängsättning:
Det har presenterats en graf där punkter som beskriver temperaturskillnaden som funktion av tiden syns som enskilda mätpunkter. (3 p.)
-
Om temperaturen har ritats i grafen i stället för temperaturskillnaden ges inga poäng för grafen.
-
Om mätpunkterna inte kan urskiljas är avdraget en poäng.
-
Om två olika anpassningar, eller en anpassning och en bruten linje, syns i grafen är avdraget en poäng.
-
Om beteckningen för en storhet eller en enhet saknas, eller om axlarna är omvända, är avdraget för varje fel en poäng.
En exponentialfunktion har presenterats som anpassning och dess uttryck har visats. (2p.)
Som svar har med 1 – 3 gällande siffrors noggrannhet givits en tid inom intervallet 580 min – 610 min. (2 p.)
Typiskt fel: Fel funktion har använts som anpassning.
10.2 Vattenflaskan ställdes tillbaka i kylskåpet efter 1,5 timmar. Kylskåpet kylde med en ideal köldfaktor, alltså \varepsilon_{\rm max}=\frac{Q}{W}=\frac{1}{\eta_{\rm max}}-1, där Q är den överförda värmemängden, W är arbetet och \eta_{\rm max} är den ideala verkningsgraden. Hur mycket extra elektrisk energi gick det åt då vattnet kyldes tillbaka ner till kylskåpets temperatur? 5 p.
Ur mätdata: \Delta T_{\rm 90\,min}=15,0\,^\circ{\rm C}-5,3\,^\circ{\rm C}=9,7\,^\circ{\rm C}.
På 1,5 timmar har vattnet värmts 9,7\,^\circ{\rm C}, alltså har vattnet mottagit värmemängden Q=cm\Delta T=20,04288\,{\rm kJ}\approx 20\,{\rm kJ}, där vattnets specifika värmekapacitet är c = 4,1819 kJ/(kg·K) och massan är m=\rho V=998,20\,\frac{\rm kg}{{\rm m}^3}\cdot 0,5\,{\rm dm}^3. Köldfaktorn kan bestämmas från den ideala verkningsgraden: \varepsilon_{\rm max}=\frac{Q}{W}=\frac{1}{\eta_{\rm max}}-1=\frac{T_2}{T_1-T_2}\approx 16,77410, där T_1=273,15\,{\rm K}+21,9\,{\rm K} och T_2=273,15\,{\rm K}+5,3\,{\rm K}.
Den elektriska energin som kylskåpet förbrukar är W=\frac{Q}{\varepsilon_{\rm max}}=cm\Delta T \frac{T_1-T_2}{T_2}=1,19487\,{\rm kJ}\approx 1,19\,{\rm kJ}.
Poängsättning:
Som svar har med 2 – 3 gällande siffrors noggrannhet givits en elektrisk energi inom intervallet 1190 J – 1230 J. (5 p.) Ifall att svaret är fel ges två poäng för en korrekt beräknad värmemängd som avges från vattnet Q = 20 kJ och två poäng för ett korrekt beräknat värde på verkningsgraden \varepsilon = 16{,}8.
Typiska fel:
-
Fel temperaturer har använts vid beräknande av värmemängden som överförs till vattnet.
-
Fel temperaturer eller grader Celsius har använts vid beräknande av verkningsgraden.
10.3 En likadan tom flaska placerades i kylskåpet som rumstempererad och sedan väntade man tills den hade nått kylskåpets temperatur. När flaskan svalnade började den skrynklas ihop när tryckskillnaden mellan flaskan och den yttre luften steg till 2,0 millibar (bild ). Bestäm arbetet som utfördes av luften inne i flaskan vid volymförändringen, då tryckskillnaden hölls konstant under hela förändringen. Förklara hur nerkylningen av luften i flaskan påverkades av att flaskan skrynklades ihop jämfört med om den inte alls hade skrynklat sig. 8 p.
Vi kan anta att luften i flaskan beter sig som en idealgas, alltså kan vi använda tillståndsekvationen för en idealgas: pV=nRT.
Substansmängden n bevaras, alltså får vi \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}, ur vilket vi får den slutliga skillnaden i volym: \Delta V = V_1-\frac{p_1V_1T_2}{T_1p_2}=V_1\Bigl(1-\frac{p_1T_2}{T_1(p_1-\Delta p)}\Bigr)
Den ursprungliga volymen var V_1=0,5\,{\rm dm}^3 , trycket p_1=101325\,{\rm Pa} , tryckskillnaden \Delta p=2,0\,{\rm mbar}=200\,{\rm Pa} och temperaturerna T_1=21,9\,{^\circ}{\rm C}=295,05\,{\rm K} och T_2=5,3\,{^\circ}{\rm C}=278,45\,{\rm K} varvid \Delta V=0,0271976\,{\rm dm}^3 , alltså ungefär 5,4 % av den ursprungliga volymen.
Trycket hölls konstant under hela hopskrynklingen, vilket ger oss arbetet W=p_2\Delta V=(p_1-\Delta p)\Delta V=(p_1-\Delta p)V_1\Bigl(1-\frac{p_1T_2}{T_1(p_1-\Delta p)}\Bigr)=V_1\Bigl((p_1-\Delta p)-p_1\frac{T_2}{T_1}\Bigr). W=2,750356\,{\rm J}\approx 2,75\,{\rm J}.
Ett arbete utförs på luften i flaskan. Enligt termodynamikens första huvudsats ökar arbete den inre energin hos luften i flaskan, samtidigt som nerkylningen minskar den. Av den här orsaken måste en större värmemängd överföras från luften i flaskan då den kyls ner. Nerkylningen tar längre tid än i fallet då luften skulle ha en konstant volym.
Poängsättning:
Tillståndsekvationen för en ideal gas har omnämnts och den har använts i en lösning. (2 p.)
Det har omnämnts att substansmängden bevaras eller substansmängdens symbol syns och substansmängdens bevarande har använts i lösningen. (2 p.)
Som svar har med 2 – 3 gällande siffrors noggrannhet givits ett korrekt beräknat arbete. (2 p.)
Genom att använda termodynamikens första huvudsats eller begreppen värme och arbete har det utan motsägelser svarats att tiden som krävs för nerkylningen måste ökas eller att en större värmemängd måste överföras från flaskan. (2 p.)
Typiska fel: Tryckets förändring har inte beaktats när flaskans volymförändring eller skrynklingsarbetet har beräknats.
11. En arbetsbeskrivning 20 p.
Några gymnasieelever gjorde en experimentell undersökning av fjäderkraft och producerade en arbetsbeskrivning utgående från undersökningen (material ).
Vid bedömningen av arbetsbeskrivningen delade läraren upp den i fem numrerade delar med streckade linjer. I varje del finns ett eller flera fel. Din uppgift är att hitta det fysikaliskt mest betydande enskilda felet i varje del. Berätta sedan hur man borde ha gått till väga, eller hur man borde ha beskrivit utförandet korrekt i arbetsbeskrivningen, i stället för att göra det här felet. Observera att endast ett fel ska nämnas i svaret för varje deluppgift.
För varje deluppgift får endast ett fel omnämnas. Den föreslagna korrigeringen ska beröra just det här felet.
Poängsättningen för alla deluppgifter gjordes enligt följande anvisningar:
Korrekt fel har identifierats i svaret. (2 p.)
Om fler än ett fel har omnämnts i svaret ges inga poäng för identifiering av svaret ifall att det inte entydigt framkommer ur svaret vilket av felen som är det mest betydande.
Det korrekta tillvägagångssättet för att korrigera felet har beskrivits i svaret. (2 p.)
Om svaret beskriver åtgärder relaterade till korrigeringen av andra fel ges inga poäng.
För alla deluppgifter fanns det två typiska fel: (i) Fler än ett fel har omnämnts. (ii) Ett fel har beskrivits, men det har inte svarats på frågan ”Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet?”
11.1 Vilket är det mest betydande felet i del 1 av arbetsbeskrivningen? Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet? 4 p.
Det mest betydande felet: Mätningarna utfördes med en (tavel)linjal, vars avläsningsnoggrannhet är onödigt grov.
Korrekt utförande: Mätningarna görs med ett mått som man kan avläsa med en noggrannhet av 1 mm, exempelvis ett rullmåttband eller en vanlig linjal.
Typiskt fel: Det påstås att det mest betydande felet är det inkorrekta värdet på gummibandets vilolängd.
11.2 Vilket är det mest betydande felet i del 2 av arbetsbeskrivningen? Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet? 4 p.
Det mest betydande felet: Det brustna gummibandet byttes ut mot ett nytt, men mätningarna startades inte om från början.
Korrekt utförande: Mätserien startas om från början när gummibandet brister, eftersom gummibanden kan ha individuella skillnader / hela mätserien utförs med samma gummiband.
Typiskt fel: Det påstås att det mest betydande felet är att stativet har fallit omkull eller att klämman har lossnat.
11.3 Vilket är det mest betydande felet i del 3 av arbetsbeskrivningen? Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet? 4 p.
Det mest betydande felet: I grafen har en överlopps mätpunkt som inte motsvarar ett riktigt mätresultat ritats i origo / det har tänkts att gummibandets längd utan en uttänjande kraft är noll.
Korrekt utförande: Överlopps punkter läggs inte till grafen, utan endast riktiga mätpunkter visas. Grafen skulle vara bättre om den ritats med gummibandets uttänjning i stället för längd, men det här är egentligen inte ett fel, eftersom fjäderkonstanten kan beräknas på båda sätten.
Typiskt fel: Det påstås att det mest betydande felet är att grafens vågräta axel visar längden i stället för uttöjningen.
11.4 Vilket är det mest betydande felet i del 4 av arbetsbeskrivningen? Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet? 4 p.
Det mest betydande felet: Resultatet (fjäderkonstanten) har beräknats från enskilda mätpunktspar.
Korrekt utförande: Mätdata används i bredare utsträckning för att bestämma fjäderkonstanten, exempelvis med hjälp av grafens lutningskoefficient.
Typiskt fel: Det påstås att det mest betydande felet är att gummibandets färg omnämns.
11.5 Vilket är det mest betydande felet i del 5 av arbetsbeskrivningen? Hur borde man ha gått till väga, eller hur borde man ha beskrivit utförandet korrekt, i stället för att göra det här felet? 4 p.
Det mest betydande felet: Resultaten generaliserades för att gälla alla uttänjningslängder.
Korrekt utförande: I arbetsbeskrivningen meddelas det att resultatet endast gäller för ett begränsat uttänjningsområde.
Typiskt fel: Det påstås att det mest betydande felet är en bristfällig användning av referenser.