Hyvän vastauksen piirteet: FI – Matematiikka, pitkä oppimäärä
26.9.2024
Lopulliset hyvän vastauksen piirteet 14.11.2024
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.
Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.
Miten pisteytysohjeita luetaan
- Ohjeen rakenne
- Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy oikeassa sarakkeessa olevaan pistemäärään.
- Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
- Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
- Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
- Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esim. derivaatan laskeminen osittain oikein).
- Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
- Suluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
- Jos erikseen ei mainita, niin vastauksen hyväksyttävä tarkkuus on yksi merkitsevä numero enemmän tai vähemmän kuin ohjeeseen kirjattu.
- Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
- Rivien riippuvuus toisistaan
- Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esim. laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
- Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
- Merkintä ylläolevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
- Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
- Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
- Teksti STOP tarkoittaa sitä, että sillä rivillä kerrotaan, minkä ehtojen pitää toteutua, jotta jatkosta tai siltä riviltä saa pisteitä.
- Terminologiaa
- ''Vastaus riittää'' tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
- ''Alkupisteitä'' tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
- ''maxN'' tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
- ''Vastaus vain likiarvona'' tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.
- Vastaus oikein, muttei pyydetyssä muodossa (esim. tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esim. e^1, ln(e) tai 4^0 -2 p.
- Vastaus sieventämättä muussa tehtävässä (esim. e^1, ln(e) tai 4^0 -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esim. x =2, y04, tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.
- Matemaattisesti puutteellinen merkintä (esim. puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
A-osa
1. Peruslaskuja 12 p.
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen osatehtävän vastaus on kokonaisluku.
1.1 Laske. 2 p.
1.1.1 1 p.
- 5 (1 p.)
1.1.2 1 p.
- 37 (1 p.)
1.2 Laske. 2 p.
- 2814 (2 p.)
1.3 Laske. 2 p.
- 7 (2 p.)
- -7 (1 p.)
- 401 (1 p.)
- 67 (1 p.)
- 19 (1 p.)
401: Ajateltu vedenkäyttö kuukausittain. (1 p.)
67: Laskettu vedenkäyttö oikein, mutta ajateltu 12 euroa kertasummana. (1 p.)
19: Yhdistetty tasauslasku ja viimeinen ennakkomaksu. (1 p.)
1.4 Laske. 2 p.
- 9 (2 p.)
1.5 Laske. 2 p.
- -2 (2 p.)
1.6 Laske. 2 p.
- 38 (2 p.)
2. Derivaattoja 12 p.
Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 3 p., väärä vastaus 0 p., ei vastausta 0 p.
Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.
2.1 Määritä luvun p’(1) tarkka arvo, kun p(x) =-2 x^5 +x^4 -2. 3 p.
- -6 (3 p.)
2.2 Määritä derivaatta f’(x), kun f(x) =x e^x. 3 p.
- (x +1) e^x (3 p.)
2.3 Määritä luvun g’(-1) tarkka arvo, kun g(x) =ln (2 x +3). 3 p.
- 2 (3 p.)
2.4 Määritä derivaatta h’(x), kun h(x) =sin x +cos (3 x). 3 p.
- cos (x) -3 sin (3 x) (3 p.)
3. Yhtälöt 12 p.
Ratkaise muuttujien x ja y tarkat arvot seuraavista yhtälöistä.
Yhtälö 4 *8^x =sqrt(2). (4 p.)
Yhtälö sin (6 y -~p /2) =1/2,, kun y in [0, ~p /2]. (8 p.)
| Yhtälö 4 *8^x =sqrt(2) voidaan kirjoittaa muodossa 2^2 *2^(3 x) =2^(1/2) (tai korotettu yhtälö puolittain toiseen potenssiin), | (1 p.) |
| joka yksinkertaistuu muotoon 2^(2 +3 x) =2^(1/2) (tai muu yhtälö, jossa samat kantaluvut molemmin puolin). | 1 p. |
| Eksponenttien vertailu: 3 x +2 =1/2 (tai muu vastaava yhtälö). | 1 p. |
| (Koska 3 x =-3/2,) saadaan melko täsmälleen x =-1/2 (tai x =-0,5). | 1 p. |
| Tähän ratkaisuun liittyvät erillisohjeet | |
| Pelkät laskut | max 4 p. |
| TAI | |
| 8^x =sqrt(2) /4 | 1 p. |
| x =log_8 (sqrt(2) /4) | 1 p. |
| =log_8 2^(-3 /2) =-3/2 log_8 2 (eli sievennetty ainakin vähän) | (1 p.) |
| melko täsmälleen x =-1/2 (tai x =-0,5). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Viimeisen pisteen saa, jos sievennys on ratkaisussa näkyvissä, vaikka vastausrivillä olisi annettu jokin muu oikea muoto. | |
| SpeedCrunch (tai ratkaisu, jossa monimutkainen lauseke ratkeaa ilman välivaiheita) | max 4 p. |
| Alussa paha laskuvirhe, esimerkiksi 4 *8^x =32^x. | max 0 p. |
| Pienempi laskuvirhe, esimerkiksi 8^x =sqrt(2) *4. (0+1+1+0) | max 2 p. |
| Ratkaisun voi aloittaa korottamalla toiseen potenssiin. Tällöin joko annetaan eksponenttimenetelmää käytettäessä 1. rivin piste, tai logaritmi-menetelmällä tästä annetaan 3. rivin piste. | |
| Vastaus sekä tarkistus, että annettu vastaus toteuttaa yhtälön (tarkoilla luvuilla eli ilman laskinta). | max 2 p. |
| Jos edellisen lisäksi perusteltu, että ei muita ratkaisuja. | max 4 p. |
| Vastaus sekä kokeilu laskimella. | max 1 p. |
| Pelkkä vastaus. | max 0 p. |
| Koska sin x =1/2, kun x =~p /6 +2 ~p k tai x =(5 ~p) /6 +2 ~p k jollain kokonaisluvulla k, (1 p., vaikka sekä suplementtikulma että 2 ~p k puuttuvat) | 1 + 1 p. |
| Sijoitetaan x =6 y -~p /2 yhtälöihin. (6 y -~p /2 =~p /6 +2 ~p k ja 6 y -~p /2 =(5 ~p) /6 +2 ~p k) | 1 p. |
| Ensimmäisestä saadaan y =~p /9 +(~p k) /3 ja toisesta y =(2 ~p) /9 +(~p k) /3. (Pisteen voi saada omilla luvuilla, mutta joko kaksi yhtälöä tai k pitää olla mukana) | 1 p. |
| Löydetty oman yhtälön oikeat k:n arvot (k in {0, 1} ensimmäisessä vaihtoehdossa ja k =0 toisessa). (1 p. per yhtälö, voi käydä ilmi implisiittisesti seuraavalta riviltä) | 2 p. |
| Ratkaisut ovat melko täsmälleen y =~p /9, y =(2 ~p) /9 ja y =~p /9 +~p /3 =(4 ~p) /9. (vähintään yksi oikea ratkaisu 1 p., kaikki oikein 2 p.) | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Voi laskea myös asteilla. | |
| Ei vaadita perusteluja sille, että ei muita vastauksia. | |
| k:t puuttuvat (eli ratkaisuina y =~p /9, y =(2 ~p) /9). (1+1+1+0+1) | max 4 p. |
| Suplementtikulma puuttuu (y =~p /9 ja y =(4 ~p) /9). (1+1+1+1+1) | max 5 p. |
| Sekä k:t että suplementtikulma puuttuvat (y =~p /9). (1+1+0+0+1) | max 3 p. |
| 2 ~p unohtunut jakaa 6:lla. (2+1+0+1+1) | max 5 p. |
| Jos ei sievennetty, vähennetään 1 p. viimeiseltä riviltä. |
4. Integraali 12 p.
Funktion f : [0, oo) -> [0, oo) arvo f(x) on luvun x kokonaislukuosa. Esimerkiksi f(1) =1, f(11/5) =2 ja f(~p) =3. Laske
int_0^10 f(x) dx.
| riippumaton Integraali mittaa funktion ja x-akselin väliin jäävän alueen pinta-alaa (voi käydä ilmi myös implisiittisesti) TAI integraali jaettu järkeviin osaväleihin. | 2 p. |
| Kyseessä on porrasfunktio, jonka arvo välillä [0, 1) on 0, välillä [1, 2) on 1, ja yleisesti välillä [k, k +1) arvo on k, kun k >= 0 on kokonaisluku. (porrasfunktio 1 p. + päätepisteet 1 p.) | 2 p. |
| Jokaisen tällaisen välin pituus on 1. (Tämä voi käydä ilmi implisiittisesti.) | (2 p.) |
| Funktion arvo puoliavoimen välin päätepisteissä ei vaikuta pinta-alaan/integraaliin. | (1 p.) |
| Laskettava pinta-ala koostuu siis suorakulmioista, joiden pinta-ala on 1 *k =k, kun k in {0, 1, 2, …, 9} TAI Laskettu jokainen väli integraalifunktion avulla. | 2 p. |
| Yhteenlaskettu ala tai integraali on siis 0 +1 +2 +3 +... +9 | 2 p. |
| = melko täsmälleen 45. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Funktio siirtynyt yhdellä portaalla, vastaus 55. (2+1+2+1+2+1+0) | max 9 p. |
| Funktio oikein, mutta pylväät/integraalit siirtyneet yhdellä portaalla, tai summassa ylimääräinen väli arvolla 10, vastaus 55. (2+2+2+1+1+1+0) | max 9 p. |
| Porraskuvio siirtynyt puolella portaalla (käytetty pyöristyssääntöä), vastaus 50. (2+1+2+1+2+1+0) | max 9 p. |
| Laskettu integraali int_0^10 x dx =50 | +0 p. |
| ''Funktio väleillä keskimäärin x -1/2, joten integraali on int_0^10 (x -1/2) dx =45'' antaa 2+1+2+1+2+2+1=11 pistettä, jos epäjatkuvuuskohtia ei ole huomioitu. Jos ne on huomioitu, voi saada enintään 12 pistettä. | max 12 p. |
| Seuraavassa numeerisella menetelmällä ei tarkoiteta suorakaidesääntöä keskipistettä käyttäen, välin pituudella 1 tai ekvivalenttia menetelmää, joka on ylläoleva oikeaoppinen ratkaisutapa. | |
| Laskettu numeerisella menetelmällä ja välien pituus korkeintaan 0,1. (2+2+2+0+1+2+0) | max 9 p. |
| Laskettu numeerisella menetelmällä ja välien pituus yli 0,1 mutta korkeintaan 1. (2+2+0+0+1+1+0) | max 6 p. |
| Laskettu numeerisella menetelmällä ja välien pituus yli 1. (2+2+0+0+0+0+0) | max 4 p. |
5. Summan arviointi 12 p.
Osoita, että (k -1) /(k 2^k +1) < 1 /2^k kaikilla positiivisilla kokonaisluvuilla k. (4 p.)
Osoita, että sum_(k =2)^n (k -1) /(k 2^k +1) < 1/2 kaikilla kokonaisluvuilla n >= 2. (8 p.)
| Järkevä avaus murtoepäyhtälön ratkaisemiseksi: muutetaan yhtäpitävään helpompaan muotoon esimerkiksi ristiinkertomalla tai laventamalla samannimisiksi. (Esimerkiksi (k -1) 2^k < k 2^k +1) | 1 p. |
| Epäyhtälön sieventäminen muotoon, josta totuusarvon voi perustella. (Esimerkiksi -2^k < 1) | 1 p. |
| Epäyhtälön totuuden perustelu (esimerkiksi huomattu, että toinen puoli on positiivinen ja toinen negatiivinen). | 2 p. |
| TAI | |
| Arvioidaan (k -1) /(k 2^k +1) < k /(k 2^k +1) < k /(k 2^k) =1 /2^k. | 4 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kokeilut | +0 p. |
| Laskuvirhe johtaa epäyhtälöön, josta oikeaa tulosta ei voi päätellä. | max 1 p. |
| Alustava työ: | |
| Vasemman puolen arviointi geometrisella summalla. | 2 p. |
| Alkutermin huomioiminen (summan alku 1/4 +1/8 +...) | 1 p. |
| Geometrisen summan laskeminen: | |
| Sovelletaan geometrisen summan kaavaa TAI geometrisen sarjan kaavaa: | |
| Oikea suhdeluku q =0,5. | 1 p. |
| Sijoitus geometrisen summan kaavaan: 1 /2^2 *(1 -1 /(2^(n-1))) /(1 -1/2) =1/2 (1 -1 /(2^(n -1))) | 2 p. |
| =1/2 -(1/2)^n | (1 p.) |
| Perusteltu, miksi geometrinen summa on alle 1/2 TAI Todettu, että äärellinen summa on pienempi kuin sarja. | 1 p. |
| TAI (toinen tapa geometrisen summan laskemiselle) | |
| Todettu, että jos oikeanpuolen summalauseke kerrotaan kahdella, saadaan geometrinen summa 1/2 +... +1 /(2^(n -1)). | 1 p. |
| Vähentämällä tästä alkuperäinen summalauseke todetaan alkuperäisen summalausekkeen arvon olevan 1/2 -(1/2)^n. | 3 p. |
| Päätelty lopputulos. | 1 p. |
| TAI (hyödyntämättä osatehtävää 5.1) | |
| Pyritty arvioimaan kahden peräkkäisen termin suhdetta. | 1 p. |
| Saatu toimivat q ja N, joilla a_(n +1) < q a_n, kun n >= N ja lisäksi q on riittävän pieni. Esimerkiksi q =2/3 ja N =2. | 3 p. |
| Laskettu geometrinen summa luvusta N alkaen (tehty sijoitukset). | 2 p. |
| Huomioitu summan alku ja viimeistelty. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Huomioitava, että tehtävä ei ratkea yrittämällä arvioida, että alkuperäisen summan seuraava termi on aina korkeintaan puolet edellisestä, koska se ei päde. Sen sijaan on mahdollista esimerkiksi arvioida kertoimella 2/3 toisesta termistä alkaen ja tämän jälkeen huomioida myös ensimmäinen termi. | |
| Kokeiltu joitakin luvun n arvoja ja tästä lopputulos. | +0 p. |
6. Veteen putoava kivi 12 p.
Mallinnetaan veteen pudonneen kiven aiheuttamia aaltoja funktiolla f: RR^2 -> RR, missä f(x, y) =sin (sqrt(x^2 +y^2)) /sqrt(x^2 +y^2), kun (x, y) !=(0, 0), ja f(0, 0) =1.
Etsi kaksi muuta pistettä, joissa funktion arvo on sama kuin pisteessä (3, 4). (6 p.)
Osoita, että jokaiselta xy-tason suoralta löytyy funktion nollakohta. (6 p.)
| f(3, 4) =sin sqrt(25) /sqrt(25) (=sin(5) /5) | 1 p. |
| ylläolevista riveistä riippumaton piste Löydetty pisteet (a, b) ja (c, d), joilla f(a, b) =f (c, d) =f(3, 4). | 1+1 p. |
| Osoitettu laskemalla, että f(a, b) =f(3, 4) | 2 p. |
| ja f(c, d) =f(3, 4). | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Arvojen vertailun voi tehdä loppuun asti sieventämättömilläkin tarkoilla arvoilla, esimerkiksi sin sqrt(25) /sqrt(25). | |
| Laskuissa riittää tarkastella pelkkiä neliöjuuren arvoja, jos yhteys tehtävään ilmenee. | |
| Laskettu ja vertailtu vain likiarvoja. (1+2+1+0) | max 4 p. |
| Tulkittu kulmien olevan asteissa. | –0 p. |
| Kun sqrt(x^2 +y^2) =k ~p ja k on positiivinen kokonaisluku, on f(x, y) =0. | 2 p. |
| Funktio saa siis arvon nolla kaikilla niillä origokeskisillä ympyröillä, joiden säde on ~p k, missä k on positiivinen kokonaisluku. | 2 p. |
| Mikä tahansa tason suora leikkaa väistämättä jotakin tällaista ympyrää, joten suoralta löytyy funktion nollakohta. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| k rajoittamatta positiivisiin kokonaislukuihin | –1 p. |
| Tarkempaa perustelua sille, miksi suora leikkaa nollakohtaympyröitä, ei vaadita. |
B1-osa
7. Geometrinen juoksuharjoittelu 12 p.
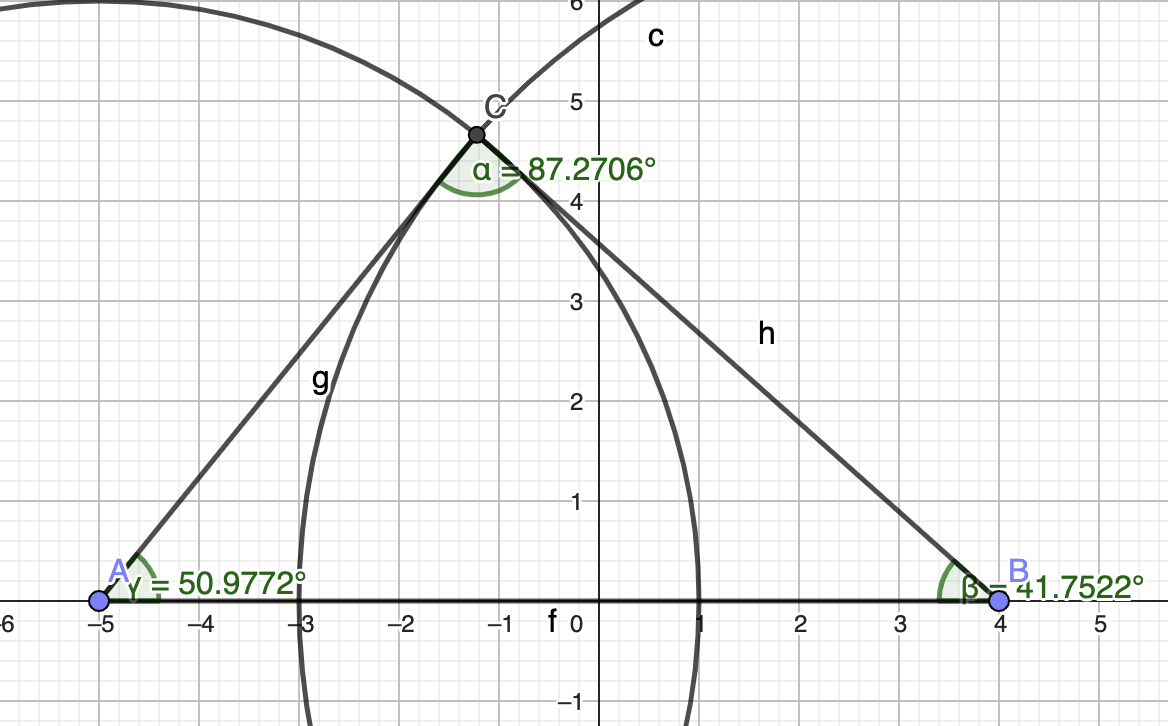
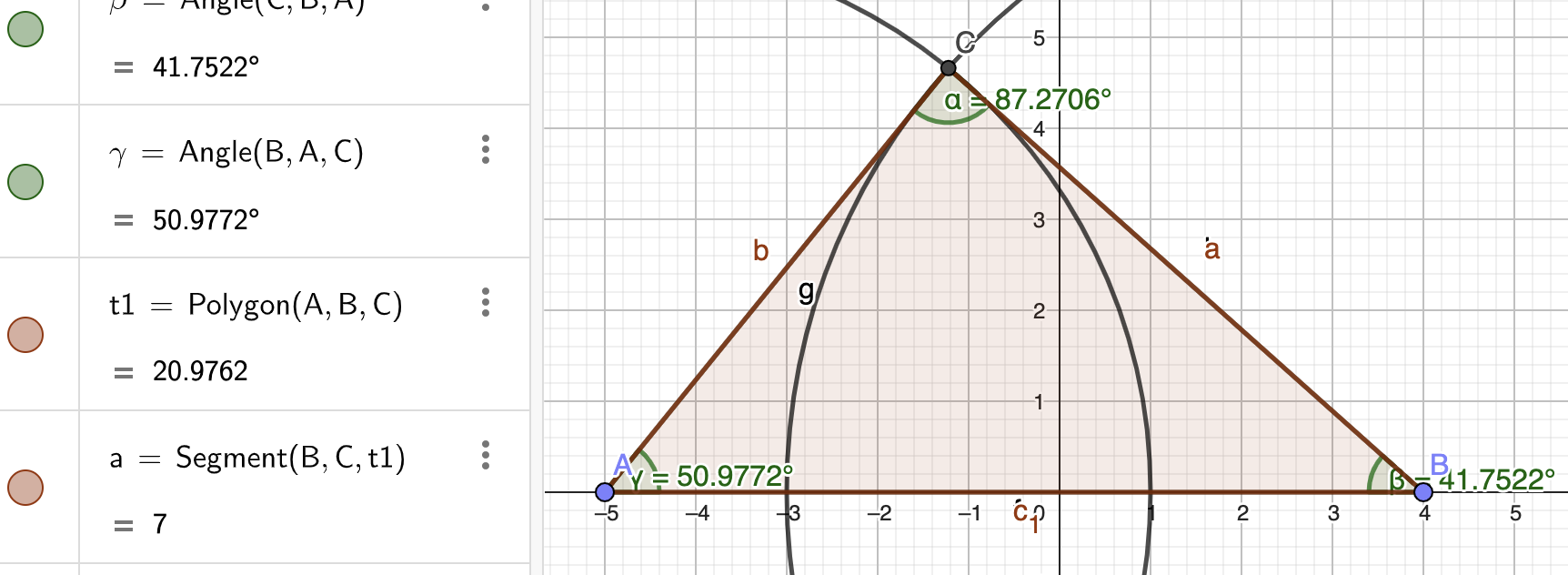
Matematiikan opettaja testasi älykelloaan juoksulenkillä. Tuloksena oli 5,85 kilometrin pituinen reitti, joka on esitetty kuvassa . Opettaja haluaa arvioida reitin sisälle jäävien kaupunginosien pinta-alaa. Hän mallintaa reittiä kolmiona, jonka sivujen pituuksien suhteet ovat 6 : 7 : 9 ja jonka piiri on 5,85 km.
Määritä mallikolmion suurin kulma asteina neljän merkitsevän numeron tarkkuudella. (6 p.)
Määritä mallikolmion pinta-ala hehtaareina. (6 p.)
| Valittu kolmion sivujen pituuksiksi 6, 7 ja 9 tai muut pituudet, joilla sivujen pituuksien suhteet ovat samat. | 1 p. |
| Kosinilauseella: Sivujen 6 ja 7 välinen kulma ~a toteuttaa ehdon 9^2 =6^2 +7^2 -2 *6 *7 *cos(~a). | 3 p. |
| SOLVE-komennolla saadaan ~a ~~87,27 ^@. (vastaus 1 p. + oikea tarkkuus 1 p.) | 2 p. |
| TAI | |
| Piirretty kuva kolmiosta, jossa sivujen pituudet (suhdeluvut tai kilometrit) likipitäen oikein. | 1 p. |
| Suurin kulma annettu neljän merkitsevän numeron tarkkuudella. | 1 p. |
| Kulma on 87,27 ^@. (2 p. tämä tarkkuus, 1 p. jos välillä 87 ^@ - 87,5 ^@-87\mathrm{,}5^{\circ}) | 2 p. |
| Perustelu, miksi kuvan kolmio on oikea, esimerkiksi komennot, joilla piirretty. (Jonkinlainen selitys 1 p., hyvä selitys 2 p.) | 2 p. |
| Muodostettu ohjelmistolla kolmio piirtämällä ensin jana, jonka pituus on 9. Piirretty sen yhteen päätepisteeseen 6-säteinen ympyrä ja toiseen päätepisteeseen 7-säteinen ympyrä. Ympyröiden leikkauspiste määrittää kolmion kolmannen kärkipisteen. Mitataan kulmat kulmanmittaustyökalulla. |
| Osatehtäväkohtaiset erillisohjeet | |
| Valittu väärä kulma. (1+2+1/1+0+1+2) | max 4 p. |
| Laskettu suorakulmaisella kolmiolla. | 0 p. |
| Tehty alussa sivuille mittakaavamuunnos väärin. (0+3+1/0+1+1+2) | max 4 p. |
| Käyttäen siniä: Koska kolmion sivujen summa on 6 +7 +9 =22 ja tämä vastaa 5,85 km lenkkiä, on yksi yksikkö kuvassa 5,85 /22 km luonnossa, | 1 p. |
| joten sivujen pituudet ovat 1,5955 sekä 1,8614 ja 2,3932. | (1 p.) |
| Sivujen 6 ja 7 välinen kulma on 87,27 ^@. Kolmion ala on siis 1/2 *6 *7 *sin(87,27 ^@) *(5,85 /22)^2 ~~1,48318 km^2. | 2 p. |
| ~~148 hehtaaria. | 2 p. |
| TAI (Käyttäen siniä ratkaisematta välissä olevaa kulmaa) | |
| Koska kolmion sivujen pituuksien summa on 6 +7 +9 =22 ja tämä vastaa 5,85 km lenkkiä, niin yksi yksikkö kuvassa vastaa 5,85 /22 kilometriä luonnossa, | 1 p. |
| joten sivujen pituudet ovat 1,5955 sekä 1,8614 ja 2,3932. | (1 p.) |
| Sivujen 6 ja 7 välisen kulman ~a kosini toteuttaa yhtälön 9^2 =6^2 +7^2 -2 *6 *7 *cos(~a) eli cos(~a) =1/21. Siispä sinin arvo on sqrt(440) /21. Kolmion ala on siis 1/2 *6 *7 *sqrt(440) /21 *(5,85/22)^2 ~~1,48318 km^2 | 2 p. |
| ~~148 hehtaaria. | 2 p. |
| TAI | |
| Mitattu kolmion pinta-ala ohjelmiston monikulmiotyökalulla. Saadaan pinta-alaksi 20,9762 yksikköä (komento tai selitys sekä vastaus). | 2 p. |
| Koska kolmion sivujen pituuksien summa on 6 +7 +9 =22 ja tämä vastaa 5,85 kilometrin lenkkiä, niin yksi yksikkö kuvassa vastaa 5,85 /22 kilometriä luonnossa. | 1 p. |
| Kolmion ala on siis 20,9762 *(5,85 /22)^2 ~~1,48318 km^2) | 1 p. |
| ~~148 hehtaaria. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Käytetty osatehtävässä 7.1 laskettua omaa kulman suuruutta, kulma ei suora. | max 6 p. |
| Käytetty suorakulmaista kolmiota. (1+1+0+2 / 1+1+0+2 / 0+1+1+2) | max 4 p. |
| Pinta-alan voi laskea myös Heronin kaavalla. | |
| Laskettu vain 1/2 *6 * 7 * sin(87,27 ^@) ~~20,9762. (0+0+2+0 / 0+0+2+0 / 2+0+0+0) | max 2 p. |
| Yksikkömuunnos väärin (1+1+2+0 / 1+1+2+0 / 2+1+1+0) | max 4 p. |
| Jos kolmion sivujen pituudet laskettu osatehtävässä 7.1, siitä annetaan pisteet tässä osatehtävässä. |
8. Tikanheitto 12 p.
Ympyränmuotoisen tikkataulun keskellä on 10 pisteen arvoinen keskiympyrä, jonka säde on 2 cm. Sen ympärillä on 9 pisteen arvoinen rengas, jonka leveys on 2 cm. Tämän renkaan ympärillä on samanlevyinen 8 pisteen rengas, sen ympärillä samanlevyinen 7 pisteen rengas ja niin edelleen uloimpaan 1 pisteen renkaaseen saakka. Tikkataulussa on siis yhteensä 10 aluetta ja koko taulun säde on 20 cm, katso kuva .
Osoita laskemalla, että parillisten pistemäärien alueiden yhteenlaskettu pinta-ala on 180 ~p cm^2. (4 p.)
Katri heittää tikkaa siten, että hän varmasti osuu tauluun, mutta voi osua mihin tahansa taulun kohtaan samalla todennäköisyydellä. Millä todennäköisyydellä Katrin tulos on parillinen, kun hän heittää kolme tikkaa ja niiden pisteet lasketaan yhteen? (8 p.)
| Renkaiden pinta-alan oikea laskuperiaate (vähennetään kahden ympyrän alat) | (1 p.) |
| Parillisia tuloksia vastaavien alueiden pinta-alat ovat neliösenttimetreinä: 10: ~p *2^2 =4 ~p 8: ~p ((3 *2)^2 -(2 *2)^2) =20 ~p 6: ~p ((5 *2)^2 -(4 *2)^2) =36 ~ 4: ~p ((7 *2)^2 -(6 *2)^2) =52 ~p 2: ~p ((9 *2)^2 -(8 *2)^2) =68 ~p (kaksi oikein 1 p., kaikki oikein 2 p.) | 2 p. |
| Näiden yhteenlaskettu pinta-ala on (4 +20 +36 +52 +68) ~p =180 ~p. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Välivaiheet vain likiarvoina (1+1+0) | max 2 p. |
| Katrin tulos on parillinen, jos hän saa kolme parillista tai kaksi paritonta ja yhden parillisen. | 1 p. |
| Koko taulun ala on ~p *20^2 =400 ~p ja parittoman alueen ala on 400 ~p -180 ~p =220 ~p. | 1 p. |
| Parittoman TAI parillisen alueen osuus laskettu. (220 ~p /(400 ~p) =11/20 =0,55 TAI 180 ~p /(400 ~p) tai 1 -220 ~p /(400 ~p) ( =9 /20 =0,45).) | (1 p.) |
| Todennäköisyys saada kolme parillista on siis (9/20)^3 =729/8000 ( =0,091125). | 1 p. |
| Todennäköisyys saada yksi parillinen ja kaksi paritonta on siis ((3), (1)) (11/20)^2 *9/20 =3267/8000 ( =0,408375). (binomikerroin + muut tulontekijät + binomitodennäköisyyden muoto.) | 3 p. |
| Yhteenlaskettu todennäköisyys on siis (3996/8000 =) melko täsmälleen 999/2000 TAI melko täsmälleen 0,4995 TAI melko täsmälleen ~~ 50 % TAI melko täsmälleen 0,5. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Komplementin ideasta ei anneta erillisiä pisteitä, välivaiheet antavat samat pisteet. | |
| Laskettu ainoastaan parittoman summan todennäköisyys 1+1+1+1+3+0. | max 7 p. |
| Väärä pinta-ala ensimmäisestä osatehtävästä. | max 7 p. |
9. Jaksollisuus 12 p.
Funktio f: RR -> RR on jaksollinen, jos on olemassa sellainen L > 0, että sen kuvaaja pysyy samana, kun sitä siirretään L yksikköä vaakasuorassa suunnassa. Tämä ominaisuus voidaan esittää myös ehdolla f(x +L) =f(x) kaikilla x in RR. Pienin tällainen luku L on funktion perusjakso.
Piirrä jokaisessa osatehtävässä funktion kuvaaja omaan koordinaatistoonsa. Anna vastauksena funktion perusjakso sekä kuvaaja, johon on merkitty perusjakson mittainen osa x-akselia.
f(x) =sin(2 ~p x) (4 p.)
g(x)=|\sin (\pi x)+\sin (2\pi x)| (4 p.)
Anna esimerkki jaksollisesta funktiosta h\colon \mathbf{R}\to\mathbf{R}, jonka perusjakso on 4. (4 p.)
| Piirretty kuvaaja, josta on vähintään kahden perusjakson mittainen osa näkyvillä ja merkitty perusjakson mittainen osa x-akselia. | 1+1 p. |
Perusjakso on 1. (1 p., jos likimäärin oikea tai annettu muu jakso kuin perusjakso) | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kuvakaappauksessa ei tarvitse näkyä komentoriviä tai funktion yhtälöä, jos se käy muuten selvästi ilmi ratkaisussa. |
| Piirretty kuvaaja, josta on vähintään kahden perusjakson mittainen osa näkyvillä ja merkitty perusjakson mittainen osa x-akselia. | 1+1 p. |
Perusjakso on 2. (1 p., jos likimäärin oikea tai annettu muu jakso kuin perusjakso) | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kuvaaja ilman itseisarvoja. (0+1+1+1) | max 3 p. |
| Kuvakaappauksessa ei tarvitse näkyä komentoriviä tai funktion yhtälöä, jos se käy muuten selvästi ilmi ratkaisusta. |
| Annettu funktio, jonka perusjakso on 4. | 2 p. |
| Piirretty funktion kuvaaja, josta on vähintään kahden perusjakson mittainen osa näkyvillä. | 1 p. |
| Merkitty funktion perusjakso. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Yllä oleva esimerkki on saatu skaalaamalla osatehtävän 9.2 esimerkki. Myös esimerkiksi \sin \left(\frac{\pi x}{2}\right) käy. | |
| Funktio, jolla väärä jakso. | 0 p. |
| Funktio, joka ei ole määritelty koko R:ssä (esimerkiksi \tan(\tfrac{\pi x}{4})). (1+1+1) | max 3 p. |
| Riittää merkitä perusjakso kuvaajaan, sitä ei tarvitse erikseen mainita. |
| Tehtäväkohtaiset erillisohjeet | |
| Jakson voi merkitä useilla erilaisilla tavoilla – yllä on esitelty kaksi mahdollista. | |
| Useita kuvaajia samassa koordinaatistossa: –1 p. funktiosta, joka ei ole omassa koordinaatistossa. (Jos esimerkiksi kaikki samassa, niin max 9.) | |
| Kuvaajan pituudessa on puutteita yhdessä tai useammassa kohdassa. Perustelujen niukkuudesta yhteensä | –1 p. |
10. Ohjelmakoodi ja tekijät 12 p.
Papu yritti selvittää positiivisen kokonaisluvun alkutekijät. Tähän tarkoitukseen hän kirjoitti Python-koodin, joka on esitetty tekstissä . Koodissa #-merkkiä seuraava teksti on kommentti, joka ei vaikuta ohjelman toimintaan. Papu ajoi ohjelman muuttujan n eri alkuarvoilla. Hän huomasi, että toisinaan ohjelma toimi virheettömästi ja tulosti luvun n alkutekijät, toisinaan se tulosti muitakin lukuja.
Osatehtävissä 10.1 ja 10.2 vastauksesta täytyy ilmetä käytetty alkuarvo ja ohjelman tuloste.
Anna esimerkki luvun n alkuarvosta, jolle ohjelma tulostaa listan, joka sisältää vain luvun n alkutekijöitä. (3 p.)
Anna esimerkki luvun n alkuarvosta, jolle ohjelma tulostaa muitakin kuin luvun n alkutekijöitä. (3 p.)
Selitä, miksi ohjelma ei aina toimi niin kuin Papu oli tarkoittanut. (6 p.)
Huomaa, että tehtävässä annettua ohjelmakoodia voi ajaa koeympäristön ohjeiden Ohjelmointi-välilehdellä. Siellä on myös Python-kielen käskyjen selityksiä.
| Ohjelma tuottaa oikean tulosteen esimerkiksi arvolla n =35, sillä tällöin se tulostaa luvut 5 ja 7. | 3 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Pelkkä kuvankaappaus tulosteesta | max 2 p. |
| Pelkkä vastaus | 0 p. |
| Alkulukusyöte | max 3 p. |
| Ohjelma ei tuota oikea tulostetta esimerkiksi arvolla n =16, sillä tällöin se tulostaa luvut 2, 4 ja 2. (Luku 4 ei ole luvun 16 alkutekijä.) | 3 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Riittää antaa vastaus ja tuloste, joten ei vähennyksiä mahdollisista ylimääräisistä virheellisistä selityksistä. | |
| Täysiin pisteisiin riittää kuvankaappaus tulosteista ja luvun n poiminta. | |
| Pelkkä vastaus | 0 p. |
| Pelkkä kuvankaappaus tulosteesta | max 2 p. |
| Jos syöte on liian suuri ja ohjelma jää jumiin, niin annetaan pisteitä, jos tulosteessa näkyy jaollisia lukuja, jotka on havaittu. | max 3 p. |
| riippumaton Oikean suuntainen selitys ongelmasta. (Esimerkiksi: Jos samaa alkutekijää löytyy useamman kerran, ohjelma voi tulostaa myös jaollisen luvun. TAI Konkreettinen esimerkki ja selitys siitä, miten koodi toimii sen kohdalla virheellisesti.) | 3 p. |
| riippumaton Toimiva korjausehdotus koodiin. TAI Ohjelma testaa kutakin luvun a arvoa vain kerran ja etenee sitten suurempaan lukuun. TAI Ohjelma ei testaa, ovatko tulosteet (tai luvut a) alkulukuja. | 3 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Aidosti virheelliset väitteet, yhteensä | –1 p. |
| Toimiva korjausehdotus koodiin ei ole vain virke ''Koodi pitäisi korjata niin, että se tulostaa vain alkutekijöitä.'', koska tämä on lähinnä tehtävänannon toistoa. Toimiva korjausehdotus sen sijaan on, jos käsketään tarkistamaan tulostettavista luvuista, ovatko ne alkulukuja. | |
| Toimimattomuuden perustelu sillä, että ohjelma jää jumiin suurilla luvuilla. | +0 p. |
| Väitetty ongelmaksi sitä, että sama alkuluku tulostuu useasti. | 0 p. |
| Täsmällinen kuvaus ongelmasta: Ohjelman for-rakenteen sisällä tulostetaan kaikki ne luvut a_1 < a_2 < … jotka toteuttavat ehdot n /a_1, n /(a_1 a_2), …, on kokonaisluku. Missään ei ole kontrollia sille, onko löydetty luku a_i alkuluku. Jos esimerkiksi n /a_1 on jaollinen jollain luvulla, joka on suurempi kuin a_1, mutta pienempi kuin seuraava alkuluku, jolla n /a_1 on jaollinen, niin a_2 ei ole alkuluku. |
| Tehtäväkohtaiset erillisohjeet | |
| Sekä osatehtävä 10.1 että osatehtävä 10.2: Epäkelpo n | max 0 p. |
| Kaikki osatehtävät: Koodi kopioitu virheellisesti ja tuottaa siksi vääriä tuloksia. | +0 p. |
B2-osa
11. Paraabelialueita 12 p.
Tarkastellaan tasojoukkoa P_0, jonka alareuna on x-akselin jana [-1, 1] ja yläreuna paraabelin kaari y =1 -x^2, -1 <= x <= 1. Arvoilla a > 0 määritellään uusi joukko P_a siirtämällä joukkoa P_0 vaakasuorassa suunnassa oikealle etäisyyden a verran. Olkoon L_a =P_0 nn P_a joukkojen P_0 ja P_a leikkaus eli yhteinen osa. Kuvassa on esimerkkinä tapaus a=0{,}75.
-
Määritä joukon L_0,75 pinta-ala. (4 p.)
Olkoon a sellainen parametrin arvo, että joukon L_a pinta-ala on puolet joukon P_0 pinta-alasta. Tämä arvo a on erään kolmannen asteen yhtälön ratkaisu. Määritä tämä yhtälö ja ratkaise siitä parametrin a likiarvo kolmen merkitsevän numeron tarkkuudella. (8 p.)
| Kun joukko siirtyy oikealle etäisyyden a verran, tarkastellaan paraabelia y =1 -(x -a)^2 TAI löydetty toisen paraabelin yhtälö. | 1 p. |
| Paraabelien leikkauspiste saadaan yhtälöstä 1 -(x -0,75)^2 =1 -x^2, josta x =0,375. | 1 p. |
| Paraabelien leikkausjoukko on symmetrinen, joten riittää laskea sen pinta-alasta puolet. Leikkauksen pinta-alaksi saadaan 2 int_-0,25^0,375 (1 -(x -0,75)^2) dx =475 /768 TAI ~~0,62. | 2 p. |
| TAI | |
| Symmetrian nojalla paraabelit leikkaavat pisteessä x =0,375. | 2 p. |
| Paraabelien leikkausjoukko on symmetrinen, joten riittää laskea sen pinta-alasta puolet. Leikkauksen pinta-alaksi saadaan 2 int_0,375^1 (1 -x^2) dx =475 /768 TAI ~~0,62. | 2 p. |
| TAI (integraalit laskettu monikulmiotyökalulla) | |
| Paraabelien leikkauksesta esitetty kuva, jossa on näkyvissä siirretyn paraabelin yhtälö. (Riittää, että kertoimet ovat kahden desimaalin tarkkuudella) | 1 p. |
| Tiheä monikulmiokonstruktio, jossa on mukana leikkauspiste (leikkauspisteen koordinaattien ei tarvitse olla näkyvissä). | 1 p. |
| Perustelut, miksi vastaus on riittävän tarkka (esimerkiksi pienempien ja suurempien monikulmioiden avulla). | 1 p. |
| Johtopäätöksenä: Vastaus 0,62 (vain, jos edellinen rivi on kunnossa). | 1 p. |
| Integroimalla saadaan P_0 =int_-1^1 (1 -x^2) dx =4/3. | 1 p. |
| Muodostettu paraabelin yhtälö. | 1 p. |
| Ratkaistaan ensin yhtälö 1 -x^2 =1 -(x -a)^2, jotta saadaan paraabelien leikkauspiste. Saadaan x^2 =(x -a)^2, joten x =a /2. | 1 p. |
| Jotta ehto toteutuu, halutaan määrittää sellainen a, että int_(a -1)^(a /2) (1 -(x -a)^2) dx =1/3. Tämä integraali antaa puolet alle jäävän alueen pinta-alasta. | 2 p. |
| Integraalin arvo on (a^3 -12 a +16) /24. | 1 p. |
| Saadaan yhtälö (a^3 -12 a +16) /24 =1/3, joka sievenee muotoon a^3 -12 a +8 =0. | 1 p. |
| Vaaditun ehdon toteuttavan ratkaisun a likiarvo on 0,695. | 1 p. |
| TAI | |
| Integroimalla saadaan P_0 =int_-1^1 (1 -x^2) dx =4/3. | 1 p. |
| Symmetrian nojalla paraabelit leikkaavat pisteessä x =a /2. | 2 p. |
| Jotta ehto toteutuu, halutaan määrittää sellainen a, että int_(a /2)^1 (1 -x^2) dx =1/3. | 2 p. |
| Integraalin arvo on (a^3 -12 a +16) /24. | 1 p. |
| Saadaan yhtälö (a^3 -12 a +16) /24 =1/3, joka sievenee muotoon a^3 -12 a +8 =0. | 1 p. |
| Vaaditun ehdon toteuttavan ratkaisun a likiarvo on 0,695. | 1 p. |
| Tehtäväkohtaiset erillisohjeet | |
| Alkupiste: Laskettu jokin pinta-ala, jonka paraabeli 1 -x^2 rajaa välillä, jonka toinen päätepiste on 1 tai -1 TAI Kuva, johon on merkitty oikea pinta-ala. | 1 p. |
12. Bézier-käyriä 12 p.
Bézier-käyriä käytetään tietokoneavusteisessa suunnittelussa (CAD), joka on vektorigrafiikan tärkeä sovelluskohde. Bézier-käyrä määritetään niin sanottujen ohjauspisteiden avulla, kuten tekstissä on kuvattu.
Eräs lineaarinen Bézier-käyrä koostuu pisteistä B(t) =(4 t, t +2), 0 <= t <= 1. Määritä tämän käyrän ohjauspisteet. (4 p.)
Erään toisen asteen Bézier-käyrän ohjauspisteet ovat P_0 =(-2, 0), P_1 =(0, 8) ja P_2 =(2, 0). Määritä käyrän yhtälö muodossa y =f(x). (8 p.)
| Tapa 1: Laskemalla | |
| Valittu välin [0, 1] päätepisteet parametrin t arvoiksi ja sijoitettu ne käyrän parametrimuotoon: (4 *0, 0 +2) ja (4 *1, 1 +2). | 1+1 p. |
| Laskettu ohjauspisteet oikein: (0, 2) ja (4, 3). | 1+1 p. |
| Tapa 2: Ohjelmisto | |
| Piirretty oikea Bézier-käyrä (liukukytkin, Käyrä() tai vastaava) | 2 p. |
| Määritetty (ei vain katsottu kuvasta) ohjauspisteet. | 1+1 |
| Osatehtäväkohtaiset erillisohjeet | |
| Huomaa, että ohjelmiston dokumentaatio, jossa on annettu käyrä ja kaksi pistettä käyrältä, ei riitä toisen rivin pisteisiin, ellei dokumentaatiosta käy ilmi, että kyseessä ovat päätepisteet. |
| Tapa 1: Sijoittaminen | |
| Ohjauspisteiden sijoitus toisen asteen Bézier-käyrän kaavaan B(t) =(1 -t) ((1 -t) (-2, 0) +t(0, 8)) +t((1 -t) (0, 8) +t(2, 0)). | 2 p. |
| Sievennys muotoon (4 t -2, 16 t -16 t^2), tai vastaava. | (2 p.) |
| Muokkaus muotoon f(x) =-x^2 +4: x =4 t -2 ja 16 t -16 t^2 =-(4 t -2)^2 +4 ja f(x) =-x^2 +4 (1+1+1) TAI Algebra-tilassa valikon kautta muunto muotoon ''Yhtälö y =ax^2 +bx +c'' (lauseke 1 p. + selitys 2 p.). | 3 p. |
| Oikea määrittelyjoukko rajoineen: -2 <= x <= 2. | 1 p. |
| TAI Tapa 2: Oletetaan käyrä paraabeliksi | |
| riippumaton Perustelu sille, että käyrä voidaan olettaa paraabeliksi. | 4 p. |
| riippumaton Perustelu symmetrialle y-akselin suhteen TAI muu perustelu sille, että huippupiste saadaan arvolla t =1/2. | 1 p. |
| Määritetty huippupiste (0, 4). | 1 p. |
| Määritetty paraabelin yhtälö. | 1 p. |
| Oikea määrittelyjoukko rajoineen: -2 <= x <= 2. | 1 p. |
13. Epäjatkuva funktio 12 p.
Olkoon f: RR -> RR,
f(x) ={3 x -5, kun x <= 1, x^2 +x -2, kun x > 1}.
Jalmari on osoittanut seuraavalla tavalla, että f’(1) =3.
Lasketaan funktion f erotusosamäärän toispuoleiset raja-arvot kohdassa x =1. Tällöin
lim_(x -> 1-) (f(x) -f(1)) /(x -1) =lim_(x -> 1-) (3 x -5 -(3 *1 -5))' /(x -1) =lim_(x -> 1-) (3 x -3) /(x -1) =lim_(x -> 1-) 3 (x -1) /(x -1) =3
ja
lim_(x -> 1+) (f(x) -f(1)) /(x -1) =lim_(x -> 1+) (x^2 +x -2 -(1^2 +1' -2)) /(x -1) =lim_(x -> 1+) (x^2 +x -2) /(x -1) =lim_(x -> 1+) ((x -1) (x +2)) /(x -1) =lim_(x -> 1+) (x +2) =3.
Koska erotusosamäärän toispuoleiset raja-arvot ovat yhtä suuret ja niiden yhteinen arvo on 3, niin funktio f on derivoituva kohdassa x =1 ja f’(1) =3.
-
Osoita, että f ei ole jatkuva kohdassa x =1. Miksi tämä on ristiriidassa Jalmarin tuloksen kanssa? Minkä virheen Jalmari tekee todistuksessaan? (6 p.)
Osoita, että f on monotoninen joukossa RR. (6 p.)
| Koska lim_(x -> 1 +) (x^2 +x -2) =0 ja lim_(x -> 1 -) (3 x -5) =-2, ei funktio ole jatkuva kohdassa x =1 (toinen raja-arvo 1 p., toinen ja johtopäätös 1 p.). | 2 p. |
| Tämä on ristiriidassa Jalmarin tuloksen kanssa, sillä funktio ei voi olla derivoituva, jos se ei ole jatkuva. (Oikeansuuntainen selitys 1 p., oikea selitys 2 p.) | 2 p. |
| Jalmarin virhe on se, että hän on erotusosamäärän lausekkeessa käyttänyt oikeanpuoleisessa raja-arvossa virheellistä arvoa f(1) =0. | 2 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Ensimmäisellä rivillä pelkkä ohjelmiston false antaa yhden pisteen. | |
| Ensimmäisellä rivillä voi verrata oikeanpuoleista raja-arvoa myös funktion arvoon. Jos oikeanpuoleisen raja-arvon sijaan on laskettu vain lausekkeen x^2 +x -2 arvo kohdassa x =1, niin ensimmäiseltä riviltä max 1. |
| Kun x < 1, on y =f(x) nouseva suora ja funktio f siis aidosti kasvava. | 1 p. |
| Kun x > 1, on f(x) polynomifunktiona derivoituva. Derivaatta on 2 x +1 > 0, eli funktio on kasvava tässä alueessa. | 2 p. |
| Lisäksi f(1) =-2 ja lim_(x -> 1 +) f(x) =0, | 2 p. |
| joten f(x) < f(y) kaikilla x <= 1 ja y > 1. | 1 p. |
| Osatehtäväkohtaiset erillisohjeet | |
| Kohta x =1 tarkastelematta. (1+2+0+0) | max 3 p. |
| Jos kolmannella rivillä oikeanpuoleisen raja-arvon sijaan on laskettu vain lausekkeen x^2 +x -2 arvo kohdassa x =1, niin kolmannelta riviltä max 1. |
| Tehtäväkohtaiset erillisohjeet | |
| Päättelyt kuvaajasta | +0 p. |