Beskrivningar av goda svar: SV – Matematik, lång lärokurs
26.9.2024
Slutgiltiga beskrivningar av goda svar 14.11.2024
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal i den högra kolumnen för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i parentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- Om inget annat anges, godkänns även en gällande siffra fler eller färre än i anvisningarna.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Ordet STOP betyder att raden beskriver villkor som måste uppfyllas för att kunna få poäng för den fortsatta lösningen.
- Terminologi
- ''Svar räcker'' betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- ''Startpoäng'' betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- ''maxN'' betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- ''Svaret endast som närmevärde'' betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (t.ex. noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (t.ex. e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (t.ex. e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (t.ex. x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (t.ex. parenteser som fattas men korrekt beräknat; =-tecknet använt ''i kedja'', m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Del A
1. Grundläggande beräkningar 12 p.
I den här uppgiften ska du endast skriva in de slutliga resultaten av uträkningarna utan mellansteg och motiveringar i svarsfälten. Svaret på varje deluppgift är ett heltal.
1.1 Beräkna. 2 p.
1.1.1 1 p.
- 5 (1 p.)
1.1.2 1 p.
- 37 (1 p.)
1.2 Beräkna. 2 p.
- 2814 (2 p.)
1.3 Beräkna. 2 p.
- 7 (2 p.)
- -7 (1 p.)
- 401 (1 p.)
- 67 (1 p.)
- 19 (1 p.)
401: Tänkt hela vattenåtgången som den månatliga åtgången. (1 p.)
67: Räknat vattenåtgången korrekt, men tänkt 12 euro som en engångssumma. (1 p.)
19: Räknat ihop sista förskottsavgiften och utjämningen till samma räkning. (1 p.)
1.4 Beräkna. 2 p.
- 9 (2 p.)
1.5 Beräkna. 2 p.
- -2 (2 p.)
1.6 Beräkna. 2 p.
- 38 (2 p.)
2. Derivator 12 p.
Välj korrekt alternativ. Svaren behöver inte motiveras. Korrekt svar 3 p., fel svar 0 p., inget svar 0 p.
Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning kan du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
2.1 Bestäm det exakta värdet för talet p'(1) då p(x)=-2x^5+x^4-2. 3 p.
- -6 (3 p.)
2.2 Bestäm derivatan f'(x) då f(x)=x e^{x}. 3 p.
- (x +1) e^x (3 p.)
2.3 Bestäm det exakta värdet för talet g'(-1) då g(x)=\ln(2x+3). 3 p.
- 2 (3 p.)
2.4 Bestäm derivatan h'(x) då h(x)=\sin x+ \cos(3x). 3 p.
- cos (x) -3 sin (3 x) (3 p.)
3. Ekvationer 12 p.
Beräkna de exakta värdena på variablerna x och y i följande ekvationer.
Ekvationen 4\cdot 8^x = \sqrt 2. (4 p.)
Ekvationen \sin(6y-\frac\pi2)=\frac{1}{2}, då y\in [0,\frac{\pi}{2}]. (8 p.)
| Ekvationen 4 *8^x =sqrt(2) kan skrivas på formen 2^2 *2^(3 x) =2^(1/2) (eller med båda leden upphöjda till två), | (1 p.) |
| vilket förenklas till 2^(2 +3 x) =2^(1/2) (eller annan ekvation med samma bas i båda leden). | 1 p. |
| Exponenterna jämförs: 3 x +2 =1/2 (eller motsvarande likhet). | 1 p. |
| (Eftersom 3 x=-3/2,) fås gaska exakt x=-\frac12 (eller x=-0{,}5). | 1 p. |
| Särskilda anvisningar för denna lösning | |
| Endast räkningar | max 4 p. |
| ELLER | |
| 8^x=\frac{\sqrt 2}{4} | 1 p. |
| x=\log_8{\frac{\sqrt{2}}{4}} | 1 p. |
| = \log_8 2^{-3/2}= -\frac32 \log_8 2 (alltså åtminstone något förenklat) | (1 p.) |
| ganska exakt x=-\frac12 (eller x=-0,5). | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Sista poängen fås om förenklingen syns i lösningen, även om svarsraden är skriven på någon annan korrekt form. | |
| SpeedCrunch (eller lösning där en komplicerad formel löses utan mellanled) | max 4 p. |
| Grovt räknefel i början, till exempel 4\cdot 8^x= 32^x. | max 0 p. |
| Mindre räknefel, till exempel 8^x=\sqrt2\cdot 4. (0+1+1+0) | max 2 p. |
| Man kan påbörja lösningen med att kvadrera båda leden. I så fall ges första radens poäng enligt exponentlösningen eller tredje radens poäng enligt logaritmlösningen. | |
| Svar samt kontroll att svaret uppfyller ekvationen (exakta värden, alltså utan räknare). | max 2 p. |
| Om man i tillägg till föregående förklarat varför det inte finns andra lösningar. | max 4 p. |
| Svar samt test med räknare. | max 1 p. |
| Endast svar. | max 0 p. |
| Eftersom sin x =1/2, då x =~p /6 +2 ~p k eller x =(5 ~p) /6 +2 ~p k för något heltal k, (1 p., även om både komplementvinkeln och 2\pi k saknas) | 1 + 1 p. |
| Substituerat x=6y-\frac{\pi}{2} i ekvationerna. (6y-\frac{\pi}{2}=\frac{\pi}{6}+2\pi k och 6y-\frac{\pi}{2}=\frac{5\pi}{6}+2\pi k) | 1 p. |
| Första ekvationen ger y =~p /9 +(~p k) /3 och den andra ger y =(2 ~p) /9 +(~p k) /3. (Poäng kan fås för egna tal, men antingen två ekvationer eller k bör förekomma) | 1 p. |
| Funnit rätt värde för k i den egna ekvationen (k\in \{0,1\} i det första alternativet och k=0 i det andra). (1 p. per ekvation, kan framgå implicit från följande rad) | 2 p. |
| Lösningarna är ganska exakt y=\frac{\pi}{9}, y=\frac{2\pi}{9} och y=\frac{\pi}{9}+\frac{\pi }{3}=\frac{4\pi}{9}. (minst en korrekt lösning 1 p., alla korrekta 2 p.) | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Kan även räknas i grader. | |
| Ingen förklaring behövs till varför inga andra lösningar finns. | |
| k saknas (alltså lösningarna y=\frac{\pi}{9}, y=\frac{2\pi}{9}). (1+1+1+0+1) | max 4 p. |
| Komplementvinkel saknas (y=\frac{\pi}{9} och y=\frac{4\pi}{9}). (1+1+1+1+1) | max 5 p. |
| Både k och komplementvinkel saknas (y=\frac{\pi}{9}). (1+1+0+0+1) | max 3 p. |
| Glömt att dividera 2\pi med 6. (2+1+0+1+1) | max 5 p. |
| Om ej förenklat, dras 1 p. bort från sista raden. |
4. Integral 12 p.
Värdet f(x) av funktionen f:[0, \infty)\to [0, \infty) är heltalsdelen av talet x. Exempelvis är f(1)=1, f(\frac{11}5)=2 och f(\pi)=3. Beräkna
\int_0^{10} f(x)\, dx.
| oberoende Integralen mäter arean av området mellan funktionsgrafen och x-axeln (kan framgå även implicit) ELLER integralen uppdelad i relevanta delintervall. | 2 p. |
| Funktionen är en trappstegsfunktion, som tar värdet 0 på intervallet [0, 1), värdet 1 på intervallet [1, 2), och i allmänhet tar värdet k på intervallet [k, k +1), då k >= 0 är ett heltal. (trappstegsfunktion 1 p. + ändpunkter 1 p.) | 2 p. |
| Varje sådant intervall har längden 1. (Detta kan framgå även implicit.) | (2 p.) |
| Funktionsvärdet i ändpunkterna av det halvöppna intervallet påverkar inte arean/integralen. | (1 p.) |
| Arean som ska beräknas består alltså av rektanglar med area 1\cdot k= k, där k\in \{0,1,2,\dots 9\} ELLER Beräknat varje intervall med en integralfunktion. | 2 p. |
| Den sammanlagda arean eller integralen är alltså 0+1+2+3+\cdots +9 | 2 p. |
| = ganska exakt 45. | 1 p. |
| Särskilda anvisningar för uppgiften | |
| Funktionen flyttad ett trappsteg, svar 55. (2+1+2+1+2+1+0) | max 9 p. |
| Rätt funktion, men staplarna/integralerna flyttade ett trappsteg, eller summan innehåller ett överflödigt delintervall med värde 10, svar 55. (2+2+2+1+1+1+0) | max 9 p. |
| Trappstegsfiguren flyttad ett halvt trappsteg (använt avrundning till närmaste heltal), svar 50. (2+1+2+1+2+1+0) | max 9 p. |
| Beräknat integralen \int_0^{10}x\, dx = 50 | +0 p. |
| ''Funktionen är i genomsnitt x-1/2 på intervallen, så integralen är \int_0^{10} (x-1/2)\, dx = 45'' ger 2+1+2+1+2+2+1=11 poäng, om diskontinuitetspunkterna inte beaktade. Om de är beaktade kan man få upp till 12 poäng. | max 12 p. |
| I vad som följer betyder numerisk metod inte rektangelregeln med värdet i mittpunkten och intervallängd 1 eller annan metod som är ekvivalent med den korrekta lösningsmetoden ovan. | |
| Beräknat med en numerisk metod med intervallängd högst 0\mathrm{,}1. (2+2+2+0+1+2+0) | max 9 p. |
| Beräknat med en numerisk metod med intervallängd större 0\mathrm{,}1, men högst 1. (2+2+0+0+1+1+0) | max 6 p. |
| Beräknat med en numerisk metod med intervallängd större än 1. (2+2+0+0+0+0+0) | max 4 p. |
5. Uppskattning av en summa 12 p.
Visa att \displaystyle\frac{k-1}{k2^k+1}<\frac{1}{2^k} för alla positiva heltal k. (4 p.)
Visa att \displaystyle\sum_{k=2}^{n}\frac{k-1}{k2^k+1}<\frac{1}{2} för alla heltal n\ge 2. (8 p.)
| Rimlig ansats för att lösa bråkolikheten: skrivit om på ekvivalent enklare form till exempel med korsvis multiplikation eller förlängning till gemensam nämnare. (Till exempel (k -1) 2^k < k 2^k +1) | 1 p. |
| Förenklat olikheten till en form från vilken man kan motivera sanningsvärdet. (Till exempel -2^k < 1.) | 1 p. |
| Motiverat att olikheten gäller (till exempel noterat att ena ledet är positivt och det andra är negativt). | 2 p. |
| ELLER | |
| Uppskattat (k -1) /(k 2^k +1) < k /(k 2^k +1) < k /(k *2^k) =1 /2^k. | 4 p. |
| Särskilda anvisningar för deluppgiften | |
| Test | +0 p. |
| Räknefel leder till en olikhet från vilket rätt resultat ej kan fås. | max 1 p. |
| Förberedande arbete: | |
| Uppskattat vänsterledet med en geometrisk summa. | 2 p. |
| Iakttagit första termen (summan börjar 1/4+1/8+\cdots ) | 1 p. |
| Räknat den geometriska summan: | |
| Tillämpat formeln för geometrisk summa ELLER formeln för geometrisk serie: | |
| Rätt kvot q=0\mathrm{,}5. | 1 p. |
| Insättning i formeln för geometrisk summa: \frac{1}{2^2}\cdot \frac{1-\frac{1}{2^{n-1}}}{1-\frac{1}{2}}=\frac{1}{2}(1-\frac{1}{2^{n-1}}) | 2 p. |
| =\frac{1}{2} - (\frac{1}{2})^n | (1 p.) |
| Förklarat varför den geometriska summan är mindre än 1/2 ELLER noterat att den ändliga summan är mindre än serien. | 1 p. |
| ELLER (ett annat sätt att beräkna den geometriska summan) | |
| Noterat att om summan i högerledet multipliceras med två, fås den geometriska summan 1/2 +\cdots + 1/2^{n-1}. | 1 p. |
| Genom att subtrahera den ursprungliga summan härifrån noterar man att den ursprungliga summan har värdet \frac{1}{2} - (\frac{1}{2})^n. | 3 p. |
| Dragit rätt slutsats. | 1 p. |
| ELLER (utan att använda deluppgift 5.1) | |
| Försökt uppskatta kvoten mellan två på varandra följande termer. | 1 p. |
| Fått fungerande tal q och N, sådana att a_{n+1}<qa_{n} då n\geq N och q är tillräckligt litet. Till exempel q=\frac{2}{3} och N=2. | 3 p. |
| Beräknat den geometriska summan från talet N (substituerat). | 2 p. |
| Tagit summans första termer i beaktande och slutfört beviset för olikheten. | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Notera att uppgiften inte kan lösas genom att försöka visa att nästa term i den ursprungliga summan alltid är högst hälften av den föregående, eftersom detta inte är sant. Däremot är det möjligt att till exempel uppskatta med en koefficient 2/3 från den andra termen, och därefter addera den första termen. | |
| Testat något värde för talet n och dragit slutsats härifrån. | +0 p. |
6. En sten faller i vattnet 12 p.
Vi gör en modell av de vågor som orsakas av en sten som faller i vattnet med funktionen f: \mathbf{R}^2\to \mathbf{R}, där \displaystyle f(x,y)=\frac{\sin\big(\sqrt{x^2+y^2}\,\big)}{\sqrt{x^2+y^2}}, då (x,y)\ne (0,0), och f(0,0)=1.
Ta fram två andra punkter i vilka funktionens värde är lika stort som i punkten (3, 4). (6 p.)
Visa att varje linje i xy-planet innehåller ett nollställe till funktionen. (6 p.)
| f(3,4)=\frac{\sin\sqrt{25}}{\sqrt{25}}\ (=\frac{\sin(5)}{5}) | 1 p. |
| poäng oberoende av de ovanstående raderna Funnit punkter (a,b) och (c,d), sådana att f(a,b)=f(c,d)=f(3,4). | 1+1 p. |
| Genom att räkna visat att f(a,b)=f(3,4) | 2 p. |
| och f(c,d)=f(3,4). | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Värdena kan jämföras helt och hållet med oförenklade exakta värden, till exempel \frac{\sin\sqrt{25}}{\sqrt{25}}. | |
| I beräkningarna räcker det att studera kvadratrötternas värden, om kopplingen till uppgiften framgår. | |
| Beräknat och jämfört närmevärden. (1+2+1+0) | max 4 p. |
| Tolkat att vinklarna var skrivna i grader. | –0 p. |
| Om sqrt(x^2 +y^2) =k ~p och k är ett positivt heltal, så gäller f(x, y) =0. | 2 p. |
| Funktionen får alltså värdet noll på alla cirklar som är centrerade i origo och har radien ~p k, där k är ett positivt heltal. | 2 p. |
| Varje linje i planet skär någon sådan cirkel, så det finns ett nollställe på linjen. | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| k inte begränsat till positiva heltal | –1 p. |
| Noggrannare argument för att linjen skär en nollställescirkel krävs inte. |
Del B1
7. Geometrisk löpträning 12 p.
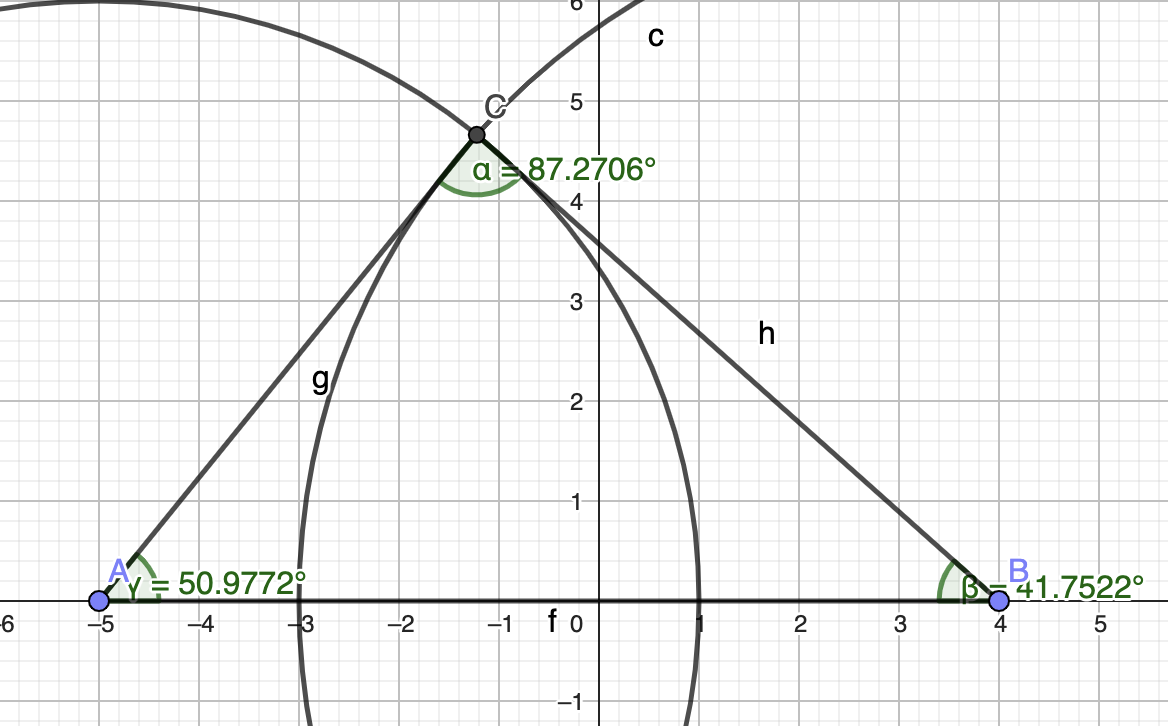
En matematiklärare testade sin smartklocka på en löprunda. Resultatet blev en 5,85 kilometer lång rutt, som presenteras i figur . Läraren vill uppskatta arean på de stadsdelar som avgränsas av rutten. Han gör en modell av rutten med en triangel: förhållandet mellan sidornas längder är 6 : 7 : 9 och triangelns omkrets är 5,85 km.
Bestäm modelltriangelns största vinkel i grader med fyra gällande siffrors noggrannhet. (6 p.)
Bestäm modelltriangelns area uttryckt i hektar. (6 p.)
| Valt en triangel med sidlängder 6, 7 och 9 eller andra längder med samma inbördes förhållanden. | 1 p. |
| Cosinussatsen: Vinkeln \alpha mellan sidorna 6 och 7 uppfyller villkoret 9^2=6^2+7^2-2\cdot 6\cdot 7\cdot \cos \alpha. | 3 p. |
| SOLVE-kommandot ger \alpha\approx 87\mathrm{,}27^{\circ}. (svar 1 p. + rätt noggrannhet 1 p.) | 2 p. |
| ELLER | |
| Ritat en triangel vars sidor (förhållandena eller kilometertalen) ungefär rätt. | 1 p. |
| Största vinkeln given med fyra gällande siffrors noggrannhet. | 1 p. |
| Vinkeln är 87\mathrm{,}27^{\circ}. (2 p. denna noggrannhet, 1 p. om inom intervallet 87^{\circ}-87\mathrm{,}5^{\circ}) | 2 p. |
| Motivering varför triangeln i bilden är korrekt, till exempel kommandon med vilka bilden ritats. (Någorlunda förklaring 1 p., god förklaring 2 p.) | 2 p. |
| Med mjukvara bildat en triangel genom att först rita en sträcka med längd 9. Därefter från denna sträckas ena ändpunkt ritat en cirkel med radie 6 och från den andra ändpunkten ritat en cirkel med radie 7. Cirkelbågarnas skärningspunkt bestämmer det tredje hörnet i triangeln. Vinklarna mäts med vinkelmätningsverktyget. |
| Särskilda anvisningar för deluppgiften | |
| Valt fel vinkel. (1+2+1/1+0+1+2) | max 4 p. |
| Räknat med rätvinklig triangel. | 0 p. |
| I början gjort felaktig omskalning av sidorna. (0+3+1/0+1+1+2) | max 4 p. |
| Med sinus: Eftersom summan av sidorna är 6+7+9=22 längdenheter, och detta svarar mot 5\mathrm{,}85 km, är en längdenhet i bilden \frac{5\mathrm{,}85}{22} km i naturen | 1 p. |
| så är sidornas längder 1\mathrm{,}5955 och 1\mathrm{,}8614 samt 2\mathrm{,}3932. | (1 p.) |
| Vinkeln mellan sidorna 6 och 7 är 87\mathrm{,}27^{\circ}. Triangelns area är alltså \frac{1}{2}\cdot 6\cdot 7\cdot \sin(87\mathrm{,}27^{\circ})\cdot \left(\frac{5\mathrm{,}85}{22}\right)^2\ (\approx 1\mathrm{,}48318 km^2). | 2 p. |
| \approx 148 hektar. | 2 p. |
| ELLER (med sinus, utan att lösa ut den mellanliggande vinkeln) | |
| Eftersom summan av sidorna är 6+7+9=22 längdenheter, och detta svarar mot 5\mathrm{,}85 km, är en längdenhet i bilden \frac{5\mathrm{,}85}{22} km i naturen | 1 p. |
| så är sidornas längder 1\mathrm{,}5955 och 1\mathrm{,}8614 samt 2\mathrm{,}3932. | (1 p.) |
| Vinkeln \alpha mellan sidorna 6 och 7 uppfyller ekvationen 9^2=6^2+7^2-2\cdot 6\cdot 7\cdot \cos \alpha, det vill säga \cos \alpha=\frac{1}{21}. Sinus har därför värdet \frac{\sqrt{440}}{21}. Triangelns area är alltså \frac{1}{2}\cdot 6\cdot 7\cdot \frac{\sqrt{440}}{21} \cdot \left(\frac{5\mathrm{,}85}{22}\right)^2\ (\approx 1\mathrm{,}48318 km^2) | 2 p. |
| \approx 148 hektar. | 2 p. |
| ELLER | |
| Mätt triangelns area med mjukvarans månghörningsverktyg. Fått arean 20\mathrm{,}9762 areaenheter (kommando eller förklaring samt svar). | 2 p. |
| Eftersom summan av triangelns sidor är 6+7+9=22 och detta motsvarar 5\mathrm{,}85 kilometers rutt, så svarar en längdenhet i bilden mot \frac{5\mathrm{,}85}{22} kilometer i naturen. | 1 p. |
| Triangelns area är alltså 20\mathrm{,}9762\cdot \left(\frac{5\mathrm{,}85}{22}\right)^2\ (\approx 1\mathrm{,}48318 km^2) | 1 p. |
| \approx 148 hektar. | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Använt egen vinkel från deluppgift 7.1, som inte är rät. | max 6 p. |
| Använt rätvinklig triangel. (1+1+0+2 / 1+1+0+2 / 0+1+1+2) | max 4 p. |
| Arean kan även räknas med Herons formel. | |
| Bara beräknat \tfrac12\cdot6\cdot7\cdot\sin(87\textrm{,}27^\circ)\approx 20\textrm{,}9762. (0+0+2+0 / 0+0+2+0 / 2+0+0+0) | max 2 p. |
| Fel i enhetsomvandlingen (1+1+2+0 / 1+1+2+0 / 2+1+1+0) | max 4 p. |
| Om sidlängderna i triangeln beräknats i deluppgift 7.1, ges poäng för detta i denna deluppgift. |
8. Pilkastning 12 p.
I mitten av en cirkelformad piltavla finns en mittcirkel som är värd 10 poäng och vars radie är 2 cm. Runt mittcirkeln finns en ring som är värd 9 poäng och vars bredd är 2 cm. Runt denna cirkel finns en 8 poängs ring med samma bredd, runt denna en 7 poängs ring med samma bredd och så vidare ända till den yttersta ringen värd 1 poäng. Piltavlan har alltså totalt 10 områden och hela tavlans radie är 20 cm, se figur .
Visa genom en beräkning att den sammanlagda arean på de områden som ger ett jämnt poängantal är 180\pi \,\text{cm} ^2. (4 p.)
Katrin kastar en pil så att hon säkert träffar tavlan, men kan träffa vilken punkt som helst på tavlan med samma sannolikhet. Med vilken sannolikhet är Katrins resultat jämnt, då hon kastar tre pilar och deras poängantal adderas? (8 p.)
| Rätt räkneprincip för att bestämma arean av ringarna (skillnaden mellan areorna av två cirklar) | (1 p.) |
| Areorna av de ringar som ger jämnt poängtal är i kvadratcentimeter: 10: \pi \cdot 2^2=4\pi 8: \pi ((3\cdot 2)^2-(2\cdot 2)^2)=20\pi 6: \pi ((5\cdot 2)^2-(4\cdot 2)^2)= 36\pi 4: \pi((7\cdot 2)^2-(6\cdot 2)^2)= 52 \pi 2: \pi((9\cdot 2)^2-(8\cdot 2)^2)=68\pi (två rätt 1 p., alla rätt 2 p.) | 2 p. |
| Deras sammanlagda area är (4+20+36+52+68)\pi=180 \pi. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Mellanleden bara närmevärden (1+1+0) | max 2 p. |
| Katrins resultat är jämnt om hon får tre jämna eller två udda och ett jämnt. | 1 p. |
| Arean av hela tavlan är ~p *20^2 =400 ~p och den udda delen av tavlan har arean 400 ~p -180 ~p =220 ~p. | 1 p. |
| Den udda ELLER den jämna delens andel av tavlan beräknad. (\frac{220 \pi}{400 \pi}(=\frac{11}{20}= 0{,}55) ELLER \frac{180 \pi}{400 \pi} eller 1-\frac{220 \pi}{400 \pi}(=\frac{9}{20}=0{,}45).) | (1 p.) |
| Sannolikheten att få tre jämna kast är alltså \left(\frac{9}{20}\right)^3=\frac{729}{8000}\ (= 0{,}091125). | 1 p. |
| Sannolikheten att få ett jämnt och två udda kast är alltså \binom{3}{1}\left(\frac{11}{20}\right)^2\cdot \frac{9}{20}=\frac{3267}{8000}\ (= 0{,}408375). (binomialkoefficient + övriga faktorer + formen för binomialsannolikheten.) | 3 p. |
| Den sammanlagda sannolikheten blir då (\frac{3996}{8000}=) ganska exakt \frac{999}{2000} ELLER ganska exakt 0{,}4995 ELLER ganska exakt \approx 50\ \% ELLER ganska exakt 0\mathrm{,}5. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Idén att beräkna komplementet ger inga särskilda poäng, annars samma poäng för mellanleden. | |
| Beräknat bara summan för udda resultat 1+1+1+1+3+0. | max 7 p. |
| Fel area från första deluppgiften. | max 7 p. |
9. Periodicitet 12 p.
Funktionen f:\mathbf{R}\to\mathbf{R} är periodisk om det finns ett sådant L>0 att dess graf hålls likadan om den flyttas L enheter i vågrät riktning. Denna egenskap kan även presenteras med villkoret f(x+L)=f(x) för varje x\in\mathbf{R}. Det minsta sådana talet L är funktionens grundperiod.
Rita i varje deluppgift funktionens graf i ett eget koordinatsystem. Ge som svar funktionens grundperiod samt grafen, i vilken en del som har grundperiodens längd är utmärkt på x-axeln.
f(x)= \sin(2\pi x) (4 p.)
g(x)=|\sin (\pi x)+\sin (2\pi x)| (4 p.)
Ge ett exempel på en periodisk funktion h\colon \mathbf{R}\to\mathbf{R}, vars grundperiod är 4. (4 p.)
| Ritat funktionsgrafen med minst två grundperioder synliga och på x-axeln markerat en del som har grundperiodens längd. | 1+1 p. |
Grundperioden är 1. (1 p., om approximativt korrekt eller om någon annan period än grundperioden givits.) | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| I en skärmdump behöver inte kommandoraden eller funktionsekvationen synas, om den annars framgår av lösningen. |
| Ritat funktionsgrafen med minst två grundperioder synliga och på x-axeln markerat en del som har grundperiodens längd. | 1+1 p. |
Grundperioden är 2. (1 p., om approximativt korrekt eller om någon annan period än grundperioden givits.) | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Graf utan absolutbelopp. (0+1+1+1) | max 3 p. |
| I en skärmdump behöver inte kommandoraden eller funktionsekvationen synas, om den annars framgår av lösningen. |
| Givit en funktion vars grundperiod är 4. | 2 p. |
| Ritat funktionsgrafen med minst två grundperioder synliga. | 1 p. |
| Markerat funktionens grundperiod. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Exemplet ovan har fåtts genom att skala exemplet i deluppgift 9.2. Även till exempel \sin \left(\frac{\pi x}{2}\right) fungerar. | |
| Funktion med fel period. | 0 p. |
| Funktion som inte är definierad på hela R (till exempel \tan(\tfrac{\pi x}{4})). (1+1+1) | max 3 p. |
| Det räcker att markera grundperioden i grafen, den behöver inte särskilt nämnas. |
| Särskilda anvisningar för uppgiften | |
| Perioden kan markeras på flera olika sätt – ovan presenteras två möjliga. | |
| Flera grafer i samma koordinatsystem: –1 p. per funktion som inte har ett eget koordinatsystem. (Om exempelvis alla funktioner ritats i samma system, så max 9.) | |
| Grafen ritad på ett för kort intervall på ett eller flera ställen. Totalt för bristande motivering | –1 p. |
10. Programkod och faktorer 12 p.
Patrik försökte ta reda på primtalsfaktorerna i ett positivt heltal. För detta ändamål skrev han en Python-kod som presenteras i text . I koden är texten efter #-tecknet en kommentar som inte påverkar programmets funktion. Patrik körde programmet med olika startvärden på variabeln n. Han märkte att programmet ibland fungerade felfritt och skrev ut primtalsfaktorerna i talet n, och ibland även skrev ut andra tal.
I deluppgifterna 10.1 och 10.2 måste det använda startvärdet och programmets utskrift framgå av svaret.
Ge ett exempel på ett startvärde för talet n, för vilket programmet skriver ut en lista som innehåller endast primtalsfaktorer i talet n. (3 p.)
Ge ett exempel på ett startvärde för talet n, för vilket programmet även skriver ut andra tal än primtalsfaktorer i talet n. (3 p.)
Förklara varför programmet inte alltid fungerar så som Patrik hade tänkt. (6 p.)
Observera att den programkod som är given i uppgiften kan köras i provmiljöns Programmering-flik. Där finns även förklaringar på Python-språkets kommandon.
| Programmet ger rätt utskrift till exempel för värdet n =35, då det skriver ut värdena 5 och 7. | 3 p. |
| Särskilda anvisningar för deluppgiften | |
| Endast skärmdump av utskriften | max 2 p. |
| Endast svar | 0 p. |
| Primtal som input | max 3 p. |
| Programmet ger inte rätt utskrift exempelvis för värdet n =16, då det skriver ut värdena 2, 4 och 2. (Talet 4 är inte en primtalsfaktor i 16.) | 3 p. |
| Särskilda anvisningar för deluppgiften | |
| Det räcker att ge ett svar och en utskrift, så inga avdrag ges för överflödiga felaktiga förklaringar. | |
| För fulla poäng räcker en skärmdump och att hitta n. | |
| Endast svar | 0 p. |
| Endast skärmdump av utskriften | max 2 p. |
| Om input är för stort och programmet kör fast, ges poäng om utskriften innehåller sammansatta tal, vilka har uppmärksammats. | max 3 p. |
| oberoende En förklaring av problemet som pekar i rätt riktning (Till exempel: Om samma primtalsfaktor förekommer flera gånger så kan programmet skriva ut sammansatta tal. ELLER Konkret exempel och förklaring på hur koden i detta fall fungerar felaktigt.) | 3 p. |
| oberoende Fungerande förslag till reparation av koden. ELLER Programmet testar varje tal a bara en gång och fortsätter sedan till större tal. ELLER Programmet testar inte om utskrifterna (eller talen a) är heltal. | 3 p. |
| Särskilda anvisningar för deluppgiften | |
| Genuint felaktiga påståenden, totalt | –1 p. |
| Som ett fungerande förslag till reparation av koden räcker inte att skriva att ''Koden bör rättas så att den bara skriver ut primtalsfaktorer.'', för detta är närmast en upprepning av uppgiftsformuleringen. Ett fungerande förslag till reparation är däremot att uppmana till att kontrollera om talen som ska skrivas ut är primtal, innan de skrivs ut. | |
| Som förklaring till att programmet inte fungerar påpekat att programet kör fast för stora värden. | +0 p. |
| Nämnt som ett problem att samma primtal skrivs ut flera gånger. | 0 p. |
| Precis beskrivning av problemet: Inom programmets for-loop skrivs alla tal a_1<a_2<\dots, ut, som uppfyller villkoret att \frac{n}{a_1}, \frac{n}{a_1a_2}, \dots är heltal. Ingenstans kontrolleras att talen a_i som hittas är primtal. Om exempelvis \frac{n}{a_1} är delbart med något tal som är större än a_1, men mindre än nästa primtal som \frac{n}{a_1} är delbart med, så är a_2 inte ett primtal. |
| Särskilda anvisningar för uppgiften | |
| Både uppgift 10.1 och 10.2: Icke lämpligt n | max 0 p. |
| Alla deluppgifter: Koden felaktigt kopierad så att den därför ger felaktiga utskrifter. | +0 p. |
Del B2
11. Parabelområden 12 p.
Vi undersöker en planmängd P_0, vars nedre kant utgörs av sträckan [-1,1] på x-axeln och övre kant utgörs av parabelbågen y=1-x^2, -1\leq x\leq 1. För värdena a>0 definieras en ny mängd P_a genom att mängden P_0 flyttas a enheter i vågrät riktning till höger. Anta att L_a=P_0\cap P_a är snittet, det vill säga den gemensamma delen av mängderna P_0 och P_a. Figur visar som exempel fallet a=0{,}75.
-
Bestäm arean av mängden L_{0{,}75}. (4 p.)
Anta att a är ett sådant värde på parametern att arean på mängden L_a är hälften av arean på mängden P_0. Detta värde a utgör en lösning på en ekvation av tredje graden. Bestäm denna ekvation och lös ut närmevärdet på parametern a med tre gällande siffrors noggrannhet ur ekvationen. (8 p.)
| När mängden flyttas a steg till höger, studerar man parabeln y =1 -(x -a)^2 ELLER funnit en ekvation för den andra parabeln. | 1 p. |
| Parablernas skärningspunkt fås genom ekvationen 1 -(x -0,75)^2 =1 -x^2, varav x =0,375. | 1 p. |
| Parablernas skärningsmängd är symmetrisk, så det räcker att beräkna halva arean. Skärningens area blir 2 int_(-0,25)^0,375 (1 -(x -0,75)^2) dx =475 /768 ELLER ~~0,62. | 2 p. |
| ELLER | |
| Av symmetriskäl skär parablerna varandra i x =0,375. | 2 p. |
| Parablernas skärningsmängd är symmetrisk, så det räcker att beräkna halva arean. Skärningens area blir 2\int_{0\mathrm{,}375}^{1}(1-x^2)\, dx=\frac{475}{768} ELLER \approx 0\mathrm{,}62. | 2 p. |
| ELLER (integrerat med månghörningsverktyg) | |
| Presenterat en bild av parablernas snitt, där parabelns ekvation är synlig. (Två decimalers noggrannhet för koefficienterna räcker) | 1 p. |
| Tät månghörningskonstruktion som inkluderar skärningspunkten (skärningspunktens koordinater behöver inte vara synliga). | 1 p. |
| Förklarat varför svaret är tillräckligt noggrannt (till exempel med en mindre och en större månghörning). | 1 p. |
| Slutsats: Svar 0\mathrm{,}62 (bara om föregående rad är i ordning). | 1 p. |
| Integrering ger P_0 =int_(-1)^1 (1 -x^2) dx =4/3. | 1 p. |
| Formulerat en ekvation för parabeln. | 1 p. |
| Först löses ekvationen 1 -x^2 =1 -(x -a)^2 för att få parablernas skärningspunkt. Vi får x^2 =(x -a)^2, så x =a /2. | 1 p. |
| För att villkoret ska uppfyllas söker vi ett sådant a, att int_(a -1)^(a /2) (1 -(x -a)^2) dx =1/3. Denna integral ger halva arean av snittet. | 2 p. |
| Integralens värde är (a^3 -12 a +16) /24. | 1 p. |
| Man får likheten (a^3 -12 a +16) /24 =1/3, som förenklas till formen a^3 -12 a +8 =0. | 1 p. |
| Lösningen a som uppfyller det önskade villkoret har närmevärdet 0,695. | 1 p. |
| ELLER | |
| Integrering ger P_0 =int_(-1)^1 (1 -x^2) dx =4/3. | 1 p. |
| Av symmetriskäl skär parablerna varandra i punkten x =a /2. | 2 p. |
| För att villkoret ska uppfyllas söker vi ett sådant a, att int_(a /2)^1 (1 –x^2) dx =1/3. | 2 p. |
| Integralens värde är (a^3 -12 a +16) /24. | 1 p. |
| Man får likheten (a^3 -12 a +16) /24 =1/3, som förenklas till formen a^3 -12 a +8 =0. | 1 p. |
| Lösningen a som uppfyller det önskade villkoret har närmevärdet 0,695. | 1 p. |
| Särskilda anvisningar för uppgiften | |
| Startpoäng: Beräknat någon area som begränsas av parabeln 1 - x^2 på något intervall som har en ändpunkt i 1 eller -1 ELLER Bild med rätt area markerad. | 1 p. |
12. Bézier-kurvor 12 p.
Bézier-kurvor används inom datorstödd design (CAD), som är ett viktigt tillämpningsområde för vektorgrafik. En Bézier-kurva definieras med hjälp av så kallade kontrollpunkter enligt beskrivningen i texten .
En linjär Bézier-kurva utgörs av punkterna B(t)=(4t, t+2), 0 \leq t\leq 1. Bestäm kontrollpunkterna för denna kurva. (4 p.)
Kontrollpunkterna till en Bézier-kurva av andra graden är P_0=(-2, 0), P_1=(0, 8) och P_2=(2, 0). Bestäm kurvans ekvation i formen y=f(x). (8 p.)
| Metod 1: Genom räkning | |
| Valt ändpunkterna till intervallet [0,1] som värden för parametern t och satt in dem i kurvans parameterform: (4 *0, 0 +2) och (4 *1, 1 +2). | 1+1 p. |
| Beräknat kontrollpunkterna korrekt: (0, 2) och (4, 3). | 1+1 p. |
| Metod 2: Med programvara | |
| Ritat rätt Bézier-kurva (glidare, Kurva() eller motsvarande) | 2 p. |
| Bestämt (inte bara tittat på bilden) kontrollpunkter. | 1+1 |
| Särskilda anvisningar för deluppgiften | |
| Notera att programvarans dokumentation, där kurvan och två punkter på kurvan är givna, inte räcker för att få andra radens poäng om det inte framgår av dokumentationen att punkterna är ändpunkter. |
| Metod 1: Substitution | |
| Placerat kontrollpunkterna i formeln för en Bézier-kurva av andra graden B(t)=(1-t)((1-t)(-2,0)+t(0,8))+t((1-t)(0,8)+t(2,0)). | 2 p. |
| Förenklat till formen (4t-2, 16t-16t^2) eller motsvarande. | (2 p.) |
| Skrivit om på formen f(x)=-x^2+4: x=4t-2 och 16t-16t^2=-(4t-2)^2+4 och f(x)=-x^2+4 (1+1+1) ELLER i menyn i Algebra-läget skrivit om som ''Ekvation y=ax^2+bx+c'' (uttryck 1 p. + förklaring 2 p.). | 3 p. |
| Rätt definitionsmängd inklusive ändpunkter: -2\leq x\leq 2. | 1 p. |
| ELLER Metod 2: Antagit att kurvan är en parabel | |
| oberoende Motiverat varför kurvan kan antas vara en parabel. | 4 p. |
| oberoende Förklarat symmetri med avseende på y-axeln ELLER annan förklaring till varför extrempunkten fås för värdet t=1/2. | 1 p. |
| Bestämt extrempunkten (0, 4). | 1 p. |
| Bestämt parabelns ekvation. | 1 p. |
| Rätt definitionsmängd inklusive ändpunkter: -2\leq x\leq 2. | 1 p. |
13. En diskontinuerlig funktion 12 p.
Anta att f:\mathbf{R}\to\mathbf{R},
f(x)=\begin{cases} 3x-5, &\text{då } x\leq 1,\\ x^2+x-2,&\text{då }x>1. \end{cases}
Hjalmar har på följande sätt visat att f'(1)=3.
Beräkning av de ensidiga gränsvärdena för differenskvoten av funktionen f i punkten x=1. Därmed är
\lim_{x\to 1-} \frac{f(x)-f(1)}{x-1}=\lim_{x\to 1-} \frac{3x-5-(3\cdot1-5)}{x-1}=\lim_{x\to 1-} \frac{3x-3}{x-1}=\lim_{x\to 1-} \frac{3(x-1)}{x-1}=3
och
\begin{split} \lim_{x\to 1+} \frac{f(x)-f(1)}{x-1}&=\lim_{x\to 1+} \frac{x^2+x-2-(1^2+1-2)}{x-1}=\lim_{x\to 1+} \frac{x^2+x-2}{x-1}\\ &=\lim_{x\to 1+} \frac{(x-1)(x+2)}{x-1}=\lim_{x\to 1+}(x+2)=3. \end{split}
Eftersom differenskvotens ensidiga gränsvärden är lika stora och deras gemensamma värde är 3, är funktionen f deriverbar i punkten x=1 och f'(1)=3.
Visa att f inte är kontinuerlig i punkten x=1. Varför strider detta mot Hjalmars resultat? Vilket fel gör Hjalmar i sitt bevis? (6 p.)
Visa att f är monoton i mängden \mathbf R. (6 p.)
| Eftersom lim_(x -> 1+) (x^2 +x -2) =0 och lim_(x -> 1-) (3 x -5) =-2, är funktionen inte kontinuerlig i punkten x =1 (ena gränsvärdet 1 p., andra gränsvärdet och slutsats 1 p.). | 2 p. |
| Detta strider mot Hjalmars resultar, för en funktion kan inte vara deriverbar om den inte är kontinuerlig. (Förklaring i rätt riktning 1 p., korrekt förklaring 2 p.) | 2 p. |
| Hjalmars fel är att han i uttrycket för differenskvoten använt fel värde f(1)=0 i högergränsvärdet. | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| I första raden ger programvarans 'false' ensamt en poäng. | |
| I första raden kan högergränsvärdet också jämföras med funktionsvärdet. Om man istället för högergränsvärdet bara beräknat värdet av uttrycket x^2+x-2 i punkten x=1, så ger första raden max 1. |
| Då x < 1, är y =f(x) en uppåtgående linje och funktionen f därför strängt växande. | 1 p. |
| Då x > 1, är f(x) en deriverbar polynomfunktion. Derivatan är 2 x +1 > 0, så funktionen är växande på detta område. | 2 p. |
| Dessutom gäller f(1) =-2 och lim_(x -> 1+) f(x) =0, | 2 p. |
| så f(x) < f(y) för alla x <= 1 och y > 1. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Inte kontrollerat punkten x=1. (1+2+0+0) | max 3 p. |
| Om man i tredje raden i stället för högergränsvärdet bara beräknat värdet av uttrycket x^2+x-2 i punkten x=1, så ger tredje raden max 1. |
| Särskilda anvisningar för uppgiften | |
| Slutsatser från grafen | +0 p. |