Hyvän vastauksen piirteet: FI – Matematiikka, lyhyt oppimäärä

26.9.2024

Lopulliset hyvän vastauksen piirteet 14.11.2024

Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.

Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.

Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.

Miten pisteytysohjeita luetaan

  • Ohjeen rakenne
    • Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy oikeassa sarakkeessa olevaan pistemäärään.
    • Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
    • Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
    • Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
    • Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esim. derivaatan laskeminen osittain oikein).
    • Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
    • Suluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
  • Jos erikseen ei mainita, niin vastauksen hyväksyttävä tarkkuus on yksi merkitsevä numero enemmän tai vähemmän kuin ohjeeseen kirjattu.
  • Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
  • Rivien riippuvuus toisistaan
    • Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esim. laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
    • Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
    • Merkintä ylläolevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
    • Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
    • Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
    • Teksti STOP tarkoittaa sitä, että sillä rivillä kerrotaan, minkä ehtojen pitää toteutua, jotta jatkosta tai siltä riviltä saa pisteitä.
  • Terminologiaa
    • ''Vastaus riittää'' tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
    • ''Alkupisteitä'' tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
    • ''maxN'' tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
    • ''Vastaus vain likiarvona'' tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.

Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.

  • Vastaus oikein, muttei pyydetyssä muodossa (esim. tarkkuus, yksikkö) -1 p.
  • Vastaus sieventämättä loppuun asti sievennystehtävässä (esim. e^1, ln(e) tai 4^0 -2 p.
  • Vastaus sieventämättä muussa tehtävässä (esim. e^1, ln(e) tai 4^0 -1 p.
  • Ilmeiset näppäilyvirheet esityksessä (esim. x =2, y04, tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
  • Vastauksessa kopiointivirhe -1 p.
  • Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.

Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.

  • Matemaattisesti puutteellinen merkintä (esim. puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
  • Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
  • Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.

A-osa

1. Arjen matematiikkaa 12 p.

Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen osatehtävän vastaus on kokonaisluku.

1.1 Laske. 2 p.

  • 14 (2 p.)

1.2 Laske. 2 p.

1.2.1 1 p.

  • 5 (1 p.)

1.2.2 1 p.

  • 37 (1 p.)

1.3 Laske. 2 p.

  • 40 (2 p.)
  • 36 (1 p.)
36: Oletettu, että kuusi annosta on kvantti, jolloin litrasta saa 36 annosta ja jää desilitra maitoa. (1 p.)

1.4 Laske. 3 p.

  • 2814 (3 p.)
  • 2905 (1 p.)
Virheellinen vastaus, joka antaa pisteen (laskettu periaatteella 4200\cdot (1-0\mathrm{,}24)(1-0\mathrm{,}09)): 2905. (1 p.)

1.5 Laske. 3 p.

  • 7 (3 p.)
  • -7 (2 p.)
  • 401 (1 p.)
  • 67 (1 p.)
  • 19 (1 p.)
-7: Ajateltu laskuun etumerkki. (2 p.)
401: Ajateltu koko vedenkäyttö kuukausittain. (1 p.)
67: Laskettu vedenkäyttö oikein, mutta ajateltu 12 euroa kertasummana. (1 p.)
19: Ajateltu viimeinen ennakkoveloitus ja tasauslasku samaan laskuun. (1 p.)

2. Yhtälö ja kolmio 12 p.

  1. Ratkaise yhtälö x^2+14=9x. (4 p.)

  2. Suora y=-2x+6 rajaa positiivisten x- ja y-akseleiden kanssa suorakulmaisen kolmion. Määritä tämän kolmion pinta-ala ja hypotenuusan pituus. (8 p.)

Muokattu muotoon x^2-9x+14=0 (vasemman puolen termien järjestyksellä ei ole merkitystä). Tämän pisteen saa myös ilman välivaihetta, jos on sijoittanut kaikki kertoimet oikein ratkaisukaavaan. 1 p.
Sijoitettu ratkaisukaavaan kertoimet 1, -9 ja 14 mahdollisesti väärään paikkaan ja eri merkein. 1 p.
Kaikki kertoimet sijoitettu ratkaisukaavaan oikein x=\frac{9\pm \sqrt{(-9)^2-4\cdot 14}}{2} TAI lisätty kuvankaappaus Speedcrunchista, josta selviää käytetyt kertoimet. 1 p.
STOP: Sijoituksessa on korkeintaan yksi merkkivirhe ja laskettu omasta ratkaisukaavasta kaksi erisuurta juurta oikein (x=2 ja x=7). 1 p.
Osatehtäväkohtaiset erillisohjeet
Kokeiluratkaisu: 1 p. per oikein tehty sijoitus ja lasku.
Ratkaisukaavan b ja c on sekoitettu, max(1+1+0+0). max 2 p.
Sijoituksessa yksi merkkivirhe, max(1+1+0+1). max 3 p.
Yhtälön muokkauksessa tehty pieni virhe, max(0+1+1+1). max 3 p.
Esimerkkejä (1+1+0+1)-tilanteesta: merkitty -9^2, laskettu oikein 81 ja saatu nollakohdiksi 2 ja 7; osoittajan alussa luvun 9 sijaan luku -9 ja saatu nollakohdiksi -2 ja -7.
Esimerkki max(1+1+0+0)-tilanteesta: merkitty -9^2, saatu -81, jonka takia juurrettava on negatiivinen.
Kateetti k_1=6 (koska suora leikkaa y-akselin kohdassa y=6). 2 p.
Kateetti k_2=3 + perustelu: suora leikkaa x-akselin, kun -2x+6=0. 1+1 p.
STOP: Jos tähän mennessä 0 p., niin ei voi saada jatkosta pisteitä.
Sijoitettu omat positiiviset kateetit kaavaan \frac{k_1\cdot k_2}{2} / melko täsmälleen saatu 9. 1+1 p.
Sijoitettu omat kateetit kaaavaan \sqrt{k_1^2+k_2^2} / melko täsmälleen saatu \sqrt{45} tai 6{,}7 tai tarkempi. 1+1 p.
Osatehtäväkohtaiset erillisohjeet
Jos rivin 1 kateetti on x-akselilla, niin -1 p. Muuten pelkkä vastaus antaa täydet pisteet ensimmäiseltä riviltä.
Jos kateetit käyvät implisiittisesti selville vasta kaavoihin sijoituksissa, niin max(1+1+2+2).
Rivin 2 perusteluksi ei kelpaa kuva, jossa suora on piirretty pisteiden (0, 6) ja (3, 0) kautta ja josta ei ole selvää, miten suora on piirretty. Suoran piirtämisen voi selittää esimerkiksi taulukoinnilla tai kulmakertoimen avulla (1 yksikkö oikealle ja 2 alas).
Neliöjuuren eteen ei vaadita \pm.
Esimerkki (2+0+1+1)-tilanteesta: Saatu kateettien pituuksiksi 6 ja 2 (koska 2x), laskettu pinta-ala \frac{6 \cdot 2}{2} = 6 ja hypotenuusan pituus \sqrt{6^2 + 2^2} \approx 6{,}3.

3. Juomalaseja mainoksessa 12 p.

Mainostoimisto suunnittelee astianpesuaineen mainosvideon. Tuottajan ajatuksena on asettaa suuri määrä juomalaseja kolmion muotoiseen kuvioon kuvan 3.A mukaisesti. Ensimmäisellä rivillä on yksi lasi, toisella rivillä kaksi, kolmannella rivillä kolme ja niin edelleen siten, että seuraavalla rivillä on aina yksi lasi enemmän kuin edellisellä rivillä.

  1. Kuinka monta juomalasia on kymmenellä ensimmäisellä lasirivillä yhteensä? (3 p.)

  2. Määritä lauseke juomalasien kokonaismäärälle, kun lasirivejä on n kappaletta. (4 p.)

  3. Kuinka monta lasiriviä on 3\,916 juomalasin muodostelmassa? (5 p.)

1+2+3+\cdots +10=55 TAI \frac{10(10+1)}2 TAI sanallinen selitys TAI hyvä kuva. 2 p.
riippumaton Vastauksena melko täsmälleen 55. 1 p.
Mainittu aritmeettinen jono tai summa, tai lauseke a_n=a_1+(n-1)d, tai kaava S_n=n\frac{a_1+a_n}2. (1 p.)
Havaittu a_1 =1 ja a_n=n. Hyväksytään myös muoto a_n=1+(n-1)\cdot 1 tai muu sellainen. 1 p.
Oikea vastaus melko täsmälleen n\frac{(1+n)}{2}. 1 p.
Perustelu aritmeettisen summalausekkeen tai yleisen kaavan S_n=n\frac{a_1+a_n}2 avulla. Edellytetään, että perustelu kohdistuu konkreettisesti tehtävän tilanteeseen. 1 p.
Osatehtäväkohtaiset erillisohjeet 1 p.
Pelkkä vastaus. 0 p.
Kahden ensimmäisen rivin pisteet voi saada muista osatehtävistä.
Muodostettu yhtälö \frac{n(n+1)}{2}=3916. 1 p.
Saatu toisen asteen yhtälö n^2+n-7832=0. 1 p.
Sijoitetaan omat toisen asteen yhtälön kertoimet ratkaisukaavaan tai SpeedCrunchiin. 1 p.
Saadaan positiivinen ja negatiivinen kokonaislukuratkaisu oikein omilla luvuilla. (n=88 tai n=-89) 1 p.
riippumaton Vastauksena melko täsmälleen 88. 1 p.
Tähän ratkaisuun liittyvät erillisohjeet
Sievennys väärin, mutta valitaan ratkaisuksi saatu luonnollinen luku (1+0+1+1+0). max 3 p.
TAI (kokeiluratkaisu)
Lasku 1+2+3+\dots+88 TAI vastaava taulukointi 1, \ldots, 88 TAI \frac{n(n+1)}2=3916 TAI 88\cdot\frac{88+1}{2}. 1 p.
Saatu laskusta tai taulukosta 3916 TAI testattu, että 88 on yhtälön ratkaisu TAI havaittu, että 88\cdot\frac{88+1}2 = 3916. 2 p.
Todetaan, että muita ratkaisuja ei ole, koska lasien lukumäärä kasvaa. 1 p.
riippumaton Vastauksena melko täsmälleen 88. 1 p.
Osatehtäväkohtaiset erillisohjeet
Käytetään osatehtävän 3.2 väärin perusteltua, mutta oikeaa lauseketta \frac{n(n+1)}2. max 5 p.
Käytetään osatehtävän 3.2 virheellistä lauseketta, joka johtaa 2. asteen yhtälöön. max 4 p.
Käytetään osatehtävän 3.2 virheellistä lauseketta, joka ei johda 2. asteen yhtälöön (1+0+0+0). max 1 p.

4. Kuulantyöntö 12 p.

Ryan Crouserin 18.2.2023 työntämän huipputuloksen perusteella on mallinnettu kuulantyönnön tulosta metreinä polynomifunktiolla

f(x)=-0{,}0126x^2+1{,}07x+0{,}630,

kun muuttuja 0\le x\le 60 on työnnön suuntakulma asteina (vaakatasosta mitattuna). Määritä derivaattaa käyttämällä suurimpaan työntötulokseen johtava työntökulma asteen sadasosan tarkkuudella ja sitä vastaava työntötulos yhden senttimetrin tarkkuudella.
Funktion derivaatta on f'(x)=2\cdot (-0\mathrm{,}0126)x+1\mathrm{,}07\,(=-0\mathrm{,}0252x+1\mathrm{,}07).
(konkreettinen yritys laskea derivaatta 1 p., derivaatan aste oikein 1 p. ja 1 p./oikea termi) 		4 p.
STOP: Ei pisteitä jatkosta, jos derivaatta ei ole ensimmäisen asteen polynomi.
Derivaatan nollakohta on x\approx 42\mathrm{,}46.
(f'(x)=0, tai maininta derivaatan nollakohdasta 1 p., sadasosan tarkkuus 1 p.) 		2 p.
riippumaton Suurin arvo löytyy joko välin päätepisteestä tai (välillä olevasta) derivaatan nollakohdasta. (Mainittu, että suurin arvo löytyy joko välin päätepisteestä tai (välillä olevasta) derivaatan nollakohdasta 1 p., laskettu funktion arvot f(0)=0{,}63 \text{ ja } f(60)=19{,}47 välin päätepisteissä 1 p.)
TAI
Koska funktion kuvaaja on alaspäin aukeava paraabeli, sillä on suurin arvo derivaatan nollakohdassa.
TAI
Tutkittu derivaatan merkkiä nollakohdan eri puolilla ja näytetty esimerkiksi kulkukaaviolla, että funktiolla on maksimi derivaatan nollakohdassa. (Yritys kulkukaaviosta 1 p.) 		2 p.
Koska derivaatan nollakohta 42,46 sijaitsee annetulla välillä [0, 60], niin suurin arvo on noin f(42{,}46)\approx 23{,}35 \text{ m}. (Todettu, että nollakohta on annetulla välillä [0, 60]. Tämä voi käydä ilmi myös kulkukaaviosta, jossa näkyvät välin päätepisteet. 1 p., laskettu funktion arvo derivaatan nollakohdassa 1 p., senttimetrin tarkkuus 1 p., yksikkö 1 p.) 4 p.
Tehtäväkohtaiset erillisohjeet
Viimeiseltä riviltä on kaikki pisteet jaossa, kunhan sinne on päästy loogisesti, vaikka olisi tapahtunut laskuvirheitä ja stop-säännön ohi on päästy.
Oman derivaatan nollakohta ei kuulu välille [0,60] ja vastattu suurin arvo päätepisteessä: viimeiseltä riviltä max(1+1+1+1).
Derivaatan nollakohta kahden desimaalin tarkkuudella riittää täysiin pisteisiin, välivaiheissa ei vaadita suurempaa tarkkuutta.
Määritetty maksimi ilman derivaattaa (esimerkiksi haarukoimalla). 0 p.
Derivaatan nollakohta haarukoimmalla ilman yksikäsitteisyyttä. max 11 p.
Rivit 1 ja 2 sekä lopussa vain f(42{,}46)\approx 23{,}35. (4+2+0+2)

5. Lainojen vertailu 12 p.

Naava ja Silmu ottavat kumpikin 9 000 euron lainan. Naavan laina on tasalyhennyslaina ja Silmun laina on annuiteettilaina. Kummankin lainan vuotuinen korkokanta on 5 % ja laina-aika 3 vuotta. He lyhentävät lainojaan kerran vuodessa. Kumman viimeinen maksuerä on suurempi?
riippumaton Korkokerroin 1+\frac{5}{100} tai 1\mathrm{,}05, tai korko 0\mathrm{,}05. 1 p.
Käytetty annuiteettikaavaa omalla korkokertoimella q ( 9000\cdot 1\mathrm{,}05^3\cdot \frac{1-1\mathrm{,}05}{1-1\mathrm{,}05^3} )
(q>1 ja sijoitus oikeaan kaavaan 1 p. / korkokerroin vastaa maksuerien lukumäärää 1 p. / 9000 kertojana 1 p.). 		3 p.
Annuiteettikaavan tulos kuuluu välille (\frac{9000}{n}, 9000) ja vastattu viimeisen/jokaisen maksuerän suuruutena (3304\mathrm{,}88). (Tässä n on maksuerien lukumäärä.) 1 p.
ylläolevista riveistä riippumaton piste Todettu: tasalyhennyslainassa kaikki lyhennykset ovat yhtäsuuria. (1 p.)
Laskettu lyhennys kaavalla \frac{9000}{n} / tulos (\frac{9000}{3}=3000). 2 p.
Viimeisen maksuerän suuruus on laskettu omien lukujen mukaisesti oikealla periaatteella (3000\cdot 1{,}05=3150 TAI 3000\cdot 0{,}05=150 / 3000+150=3150). 2 p.
Luvut täsmälleen 3304{,}88 ja 3150{,}00, ja vertailun perusteella viimeinen erä on siis suurempi Silmun/annuiteettilainalla / pienempi Naavan/tasaerälainalla (molemmat oikeat luvut 1 p. Johtopäätöksenä: vertailu ja johtopäätös 1 p.). 2 p.
Tähän ratkaisuun liittyvät erillisohjeet
Välipyöristykset ok, tarkkuus ainakin 2 merkitsevää numeroa.
Kuukausilyhennykset (q=1\mathrm{,}004167, erät: 36, vertaillaan 268\mathrm{,}74>251\mathrm{,}04). (0+3+1+1+2+2+0). max 9 p.
Korkokerroin q=1\mathrm{,}005 tai q=1\mathrm{,}0005 (0+3+1+1+2+2+0). max 9 p.
Korkokerroin q=0\mathrm{,}05 (0+1+0+1+2+2+0). max 6 p.
Lainoissa käytetty eri korkokerrointa/korkoa, joista toinen on oikein. (1+2+1+1+2+2+0) TAI (1+3+1+1+2+1+0) max 9 p.
Esimerkiksi tasalyhennyslainassa laskettu \frac13 \cdot (1{,}05 \cdot 9000) = 3150 tai 9450 välivaiheessa riveiltä 4–6 (0+1+2). Jos lisäksi selkeästi kirjoitettu ''tasalyhennyslainassa kaikki lyhennykset ovat yhtä suuria'', niin (1+1+2). max 8–9 p.
Esimerkiksi laskettu ilman selityksiä 9000/3=3000 ja 1{,}05\cdot 3000=3150. Riveiltä 4–6 (1+2+2) ja -1 p. huonoista selityksistä. Viimeisen rivin pisteet jäävät saamatta. max 9 p.
TAI
Tasalyhennyslainassa maksuerät pienenevät ja annuiteettilainassa erät pysyvät samoina. 1 p.
Jos annuiteettilainan viimeinen maksuerä olisi pienempi (tai yhtäsuuri) kuin tasalyhennyslainan viimeinen maksuerä, olisivat kaikki annuiteettilainan maksuerät pienempiä kuin tasalyhennyslainan (viimeinen yhtäsuuri). 5 p.
Koska lainoilla on sama korko, eivät annuiteettilainan maksuerät voisi tällöin olla riittävät / tasalyhennyslainassa maksettaisiin liikaa. (Jos annuiteettilainan viimeinen maksuerä olisi pienempi tai yhtäsuuri kuin tasalyhennyslainan viimeinen maksuerä 1{,}05 \cdot 3000 euroa, olisivat kaikki annuiteettilainan maksuerät pienempiä tai yhtäsuuria. Näin annuiteettilainaa maksettaisiin < 1{,}05 \cdot 9000 euroa, mikä ei ole mahdollista 5 % vuosikorolla ja vuosittaisilla erillä.) 4 p.
Johtopäätöksenä: Näin ollen viimeinen erä on suurempi (Silmun) annuiteettilainalla. 2 p.

6. Jakaumia, kuvaajia ja todennäköisyyksiä 12 p.

Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 2–3 p., väärä vastaus 0 p., ei vastausta 0 p.

Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.

6.1 Yhdistä seuraaviin väitteisiin sopiva onnistumistodennäköisyyden jakauma kuvasta 6.A. Heitetään kerran kahta noppaa ja tavoitteena on saada 6 p.

6.1.1 2 p.

  • Jakauma 1  (2 p.)
Kahden nopan heitossa kummankin nopan silmäluku on parillinen: jakauma 1.

6.1.2 2 p.

  • Jakauma 3  (2 p.)
Kahden nopan heitossa silmälukujen tulo on parillinen luku: jakauma 3.

6.1.3 2 p.

  • Jakauma 4  (2 p.)
Kahden nopan heitossa silmälukujen summa ei ole kolmella jaollinen: jakauma 4.

6.2 Korttipakassa on neljä maata, joista kussakin kortit numeroilla 2–10. Pakasta nostetaan kaksi korttia ilman takaisinpanoa. 6 p.

6.2.1 3 p.

  • ei mikään ylläolevista  (3 p.)

6.2.2 3 p.

  • \frac{17}{21}  (3 p.)

B-osa

7. Piparkakkurasiat 12 p.

Joulun piparkakut pakataan kolmeen erikokoiseen ympyräpohjaiseen peltirasiaan, jotka näkyvät kuvassa 7.A.

  • Suurimman rasian ympärysmitta on 78,5 cm ja korkeus on 10,0 cm.

  • Keskimmäisen rasian säde on 1,5 cm pienempi ja korkeus 1,0 cm pienempi kuin suurimman rasian.

  • Pienimmän rasian säde on 2,5 cm pienempi ja korkeus 1,0 cm pienempi kuin keskimmäisen rasian.

Laske rasioiden yhteistilavuus desilitran tarkkuudella.

Laskettu suurimman rasian halkaisija 78{,}5/\pi \approx 24{,}99. (1 p.)
Esitetty säteelle lauseke 78{,}5/(2\pi) TAI muodostettu yhtälö 78{,}5=2\pi r. 1 p.
ylläolevista riveistä riippumaton piste Säde on melko täsmälleen 12{,}49\approx 12{,}5 (tai tarkempi). 1 p.
STOP: Tämän rivin pisteet voi saada vain, jos ison purkin säde on muodostettu oikein. Laskettu keskimmäisen ja pienimmän rasian säteet vähentämällä 1,5 ja 4. (oikeat tulokset 10{,}99 ja 8{,}49 tai 11 ja 8{,}5). 1+1 p.
ylläolevista riveistä riippumaton piste Keskimmäisen ja pienimmän rasian korkeudet 9{,}0 ja 8{,}0 (tai 9 ja 8). 1 p.
Tilavuuden laskussa oikea kaava ja omat luvut sijoitettu oikein (\pi (12{,}49)^2 \cdot 10{,}0, \pi (10{,}99)^2 \cdot 9{,}0 ja \pi (8{,}49)^2 \cdot 8{,}0). Säteet ja korkeudet samassa yksikössä tai yksiköt merkitty näkyviin, muuten 0 p. 1 p.
Ympyrälieriön tilavuuden laskussa lähtölukujen yksiköt oikein tai tilavuusyksikkö oikein ja näkyvissä laskussa tai myöhemmin. 1 p.
STOP: Seuraavilta riveiltä voi saada pisteitä vain, jos on laskettu ympyrälieriön tilavuutta ja tilavuusyksikkö on oikein ja näkyvissä laskussa tai myöhemmin.
Tilavuuksien summa laskettu (4903{,}763+3417{,}254+1813{,}134 = 10134{,}151~\text{cm}^3). Tehty oikea yksikkömuunnos desilitroiksi tai litroiksi. Esityksestä on käytävä ilmi, minkä yksiköiden välillä muunnos tehdään, muuten 0 p. 1+2 p.
Summa on laskettu, yksikkömuunnos on oikein ja vastaus esitetty desilitran tarkkuudella (101 (dl) tai 10{,}1 l, tai muu yksikkö selitettynä, miksi se on oikea tarkkuus). 1 p.
Tehtäväkohtaiset erillisohjeet
Rivit 4 ja 8 eivät edellytä laskulauseketta, kunhan tulokset voi tulkita selkeästi kaavan perusteella tai selityksistä.
Jos rivillä 6 on oikea kaava ja oikeat sijoitukset, mutta on tehnyt tilavuuslaskussa laskuvirheen, saa rivin 6 pisteen, mutta menettää pisteen tilavuuden summasta riviltä 8.
Käytetty halkaisijaa koko laskun ajan ja myös tilavuuden laskussa, esimerkiksi rivillä 5 on \pi(24{,}99)^2 \cdot 10{,}0 (1+0+0+0+1+1+1+3+1). max 8 p.
Tulkittu tehtävä niin, että 1{,}5 ja 4 on vähennetty halkaisijasta, ei säteestä, muuten oikein (kaikki pisteet paitsi rivi 4). max 10 p.
Ohjelmistolla tehdyssä ratkaisussa pitää olla samat välivaiheet. Lisäksi laskut/komennot tulee olla näkyvissä. Jos esimerkiksi säde on määritelty riittävän tarkasti kokeilemalla, niin alusta (0+0+1+\ldots).

8. Moottoritien kustannukset 12 p.

Helsingin Sanomat kirjoitti 20.6.1972:

Vuonna 2018 valmistuneessa tiehankkeessa Haminasta Vaalimaalle kulkevan 32 kilometrin pituisen moottoritieosuuden hinta oli 550 miljoonaa euroa. Tässä tehtävässä eri vuosien kustannuksia verrataan käyttämällä "Aku Ankka -indeksiä", joka perustuu seuraavaan tietoon: Aku Ankka -lehden irtonumero maksoi 0,80 markkaa vuonna 1972 ja 3,50 euroa vuonna 2018.

Mitkä olivat Helsinki–Lahti-moottoritien kustannukset vuoden 2018 rahassa?

Kuinka monta prosenttia kalliimpi Hamina–Vaalimaa-moottoritie oli kilometriä kohti kuin Helsinki–Lahti-moottoritie rahan arvon muutos huomioiden?

Helsinki–Lahti-moottoritien kustannukset nykyrahassa:
Aku Ankan hinnan perusteella voidaan arvioida, että rahan arvo on muuttunut suurin piirtein kertoimella \frac{3\mathrm{,}50}{0\mathrm{,}80}\, (\frac{\textrm{euro}}{\textrm{mk}})=4\mathrm{,}375\, (\frac{\textrm{euro}}{\textrm{mk}}) TAI jakajalla \frac{0\mathrm{,}80}{3\mathrm{,}50}\, (\frac{\textrm{mk}}{\textrm{euro}})=0\mathrm{,}22857142857\ldots (\frac{\textrm{mk}}{\textrm{euro}}) TAI muodostetaan verrannollisuusyhtälö \frac{0\mathrm{,}80}{3\mathrm{,}50}=\frac{320}{x}. 2 p.
Kokelas on ymmärtänyt valuutan muutoksen vertailun oikein (esimerkiksi taulukko tai verrantoyhtälö tai käytetty kerrointa oikein). 1 p.
Kustannukset olivat siis 320\cdot 4\mathrm{,}375 TAI 320:0\mathrm{,}22857142857 TAI 320\cdot \frac{3\mathrm{,}50}{0\mathrm{,}80} 2 p.
= melko täsmälleen 1400 miljoonaa euroa. 1 p.
Kustannusten vertailu:
Käyttämällä vuoden 2018 rahan arvoja
Hamina–Vaalimaa maksoi \frac{550\,000\,000}{32}=17187500 euroa kilometriä kohti. 2 p.
ylläolevista riveistä riippumaton piste Helsinki–Lahti maksaisi 3\cdot 10^6\cdot 4\mathrm{,}375 \, (\frac{\textrm{euro}}{\textrm{km}}) (=13\,125\,000 \,(\frac{\textrm{euro}}{\textrm{km}})). (kilometrin hinta 1 p. ja muunnos markoista euroiksi 1 p.) 2 p.
Lasketaan vertailuprosentti oikealla periaatteella (esimerkiksi \frac{17\,187\,500-13\,125\,000}{13\,125\,000}). 1 p.
Uusi moottoritie on siis noin täsmälleen 31 % kalliimpi kuin vanha. 1 p.
Laskettu tiedon 3 mk/mm avulla Helsinki–Lahti moottoritien pituus ja kilometrihinta.
Hamina–Vaalimaa maksoi \frac{550\,000\,000}{32}=17\,187\,500 euroa kilometriä kohti. 2 p.
ylläolevista riveistä riippumaton piste Lasketaan Helsinki–Lahti-moottoritien pituutta oikealla periaatteella: \frac{320 \cdot 10^6\, (\textrm{mk})}{3 (\frac{\textrm{mk}}{\textrm{mm}})}\, (= \frac{320}{3} (\textrm{km}) \approx 106\mathrm{,}666\ldots (\mathrm{km})). 1 p.
Lasketaan Helsinki–Lahti-moottoritien hintaa oikealla periaatteella: \frac{1\,400\,000\,000(\textrm{euro})}{\frac{320}{3}(\textrm{km})}\,(=13\,125\,000 (\frac{\textrm{euro}}{\text{km}})). 1 p.
Lasketaan vertailuprosentti oikealla periaatteella (esimerkiksi \frac{17\,187\,500-13,125\,000}{13\,125\,000}). 1 p.
Uusi moottoritie on siis noin täsmälleen 31 % kalliimpi kuin vanha. 1 p.
Käyttämällä vuoden 1972 arvoja
Hamina–Vaalimaa maksoi \frac{550\,000\,000}{32}=17\,187\,500 euroa kilometriä kohti. 2 p.
Lasketaan oikealla periaatteella Hamina–Vaalimaan kustannuksia kilometria kohti vuoden 1972 rahassa 17\,187\,500 \cdot \frac{8}{35}=\frac{27\,500\,000}{7}\approx 3\,928\,571\mathrm{,}42 markkaa. 1 p.
ylläolevista riveistä riippumaton piste Helsinki–Lahti esimerkiksi 3 \,(\frac{\textrm{mk}}{\textrm{mm}})= 3 \cdot 10^6 \,(\frac{\textrm{mk}}{\textrm{km}}) = 3 miljoonaa markkaa kilometriä kohti. 1 p.
Lasketaan vertailuprosentti oikealla periaatteella \frac{\frac{27\,500\,000}{7}-3\cdot 10^6}{3\cdot 10^6}. 1 p.
Uusi moottoritie on siis noin täsmälleen 31 % kalliimpi kuin vanha. 1 p.
Tehtäväkohtaiset erillisohjeet
Ilmaisulla ''Lasketaan vertailuprosentti oikealla periaatteella'' tarkoitetaan kustannus jaettuna pituudella -tilannetta, luvut samassa yksikössä ja vertaillaan vanhaan kustannukseen.

9. Perusteltu binomijakauma 12 p.

Noppaa heitetään kuusi kertaa. Todennäköisyys saada silmäluku 6 täsmälleen neljä kertaa on binomitodennäköisyyden kaavan mukaan

{6 \choose 4} \big(\tfrac16\big)^4 \big(\tfrac56\big)^2 = \frac{125}{15552} \approx 0{,}00804.

Selitä käytetty kaava ja kaikki siinä esiintyvät osat, eli perustele binomitodennäköisyyden kaava tässä tilanteessa.

Selitetään minkä tahansa yhden heittojonon todennäköisyys
1/6 on todennäköisyys saada silmäluku 6 yhdellä heitolla. 1 p.
(1/6)^4 on todennäköisyys saada silmäluku 6 neljällä heitolla. 2 p.
5/6 on todennäköisyys saada jokin muu kuin silmäluku 6 yhdellä heitolla. 1 p.
(5/6)^2 on todennäköisyys saada jokin muu kuin silmäluku 6 kahdella heitolla. 2 p.
Todennäköisyydet (1/6)^4 ja (5/6)^2 kerrotaan keskenään, koska halutaan saada selville sen todennäköisyys, että molemmat tapahtumat toteutuvat samalla kertaa. 1 p.
Selitetään kaikkien heittojonojen lukumäärä ja kokonaistodennäköisyys
Binomikerroin \binom{6}{4} kertoo sen, miten monta erilaista suotuisaa heittojonoa on. 2 p.
Selitetty lukujen 6 ja 4 merkitys binomikertoimessa. Esimerkiksi: mahdollisia paikkoja jonossa on kuusi kappaletta ja näistä valitaan ne neljä, joihin tulee kuutonen TAI kuinka monella tavalla (heittojonolla) voidaan kuudesta heitosta valita ne neljä heittoa, joilla saadaan silmäluku kuusi TAI moneenko järjestykseen, esimerkiksi jonoon, neljä kuutosta ja kaksi jotain muuta silmälukua voidaan asettaa. 1 p.
Todettu, että heittojonot ovat yhtä todennäköisiä tai tämä ilmenee ratkaisusta (1 p.). Yksittäisen jonon todennäköisyys kerrotaan binomikertoimella, jotta saadaan laskettua kaikkien eri heittojonojen kokonaistodennäköisyys (1 p.). 2 p.
Tehtäväkohtaiset erillisohjeet
Monet kohdat ovat riippumattomia, eikä niitä ole erikseen merkitty.
Ei pisteitä prosessin kuvauksesta, esimerkiksi ''Sijoitetaan 6 ylös koska se on heittojen määrä ja 4 alas koska se on suotuisten tapausten lukumäärä'' ei anna pisteitä rivillä 7.

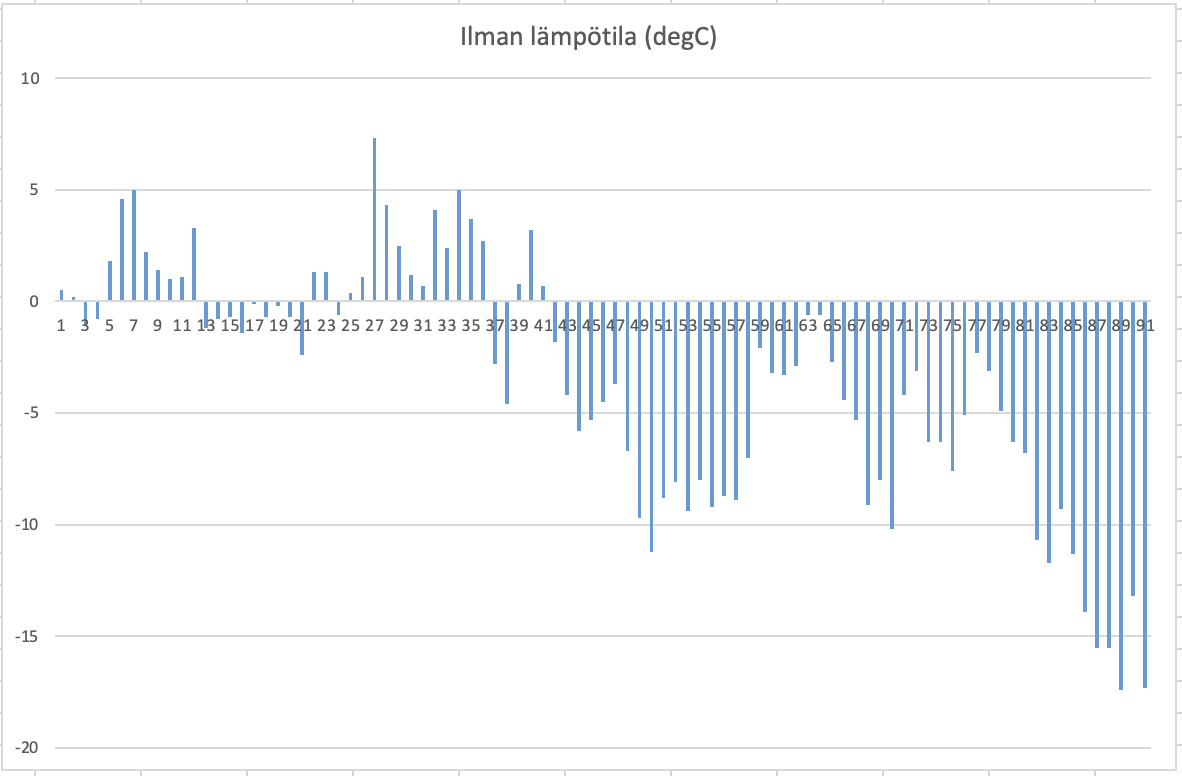
10. Terminen talvi 18 p.

Valitse osatehtävissä 10.1–10.2 oikea vaihtoehto. Näitä vastauksia ei tarvitse perustella. Oikea vastaus 1–2 p., väärä vastaus 0 p., ei vastausta 0 p. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.

Tarkastellaan Saanan havaintoaseman lämpötiloja taulukosta 10.B käyttäen tekstin 10.A käsitteitä. Teksti on Ilmatieteen laitoksen termisiä vuodenaikoja koskeva esitys kokonaisuudessaan. Tehtävän ratkaisua varten täytyy tekstistä hakea itse tarvittavat tiedot.

10.1 Valitse oikea vaihtoehto. 2 p.

10.1.1 1 p.

  • 7  (1 p.)

10.1.2 1 p.

  • 27.9.  (1 p.)

10.2 Valitse oikea vaihtoehto. 2 p.

  • 1  (2 p.)

10.3 Kirjoita osatehtävien 10.3.1 ja 10.3.2 vastaukset vastauskenttään. 14 p.

10.3.1 Piirrä pylväsdiagrammi päivittäisistä keskilämpötiloista. 4 p.
Piirretty pylväsdiagrammi, jossa on vähintään 3 pylvästä, ja ne liittyvät annettuun dataan. 1 p.
Piirretty pylväsdiagrammi, jossa on kaikki silmämääräisesti oikeat pylväät (voi olla muitakin pylväitä). 1 p.
Pylväsdiagrammissa on oikea määrä pylväitä ja ne kaikki ovat oikein. 1 p.
Pylväsdiagrammin akseleilla päivämäärät ja lämpötilat esitetty ja selitetty selvästi. 1 p.
Osatehtäväkohtaiset erillisohjeet
Kolmannen rivin pistettä ei anneta, jos kuvassa on ylimääräisiä pylväitä.
Ylimääräiset selitteet, esimerkiksi ''sininen väri sarake D'' tai ''sininen väri 0,5''. –0 p.
Pylväiden ei tarvitse välttämättä alkaa 0 asteesta, vaan ne voivat alkaa esimerkiksi -20 asteesta.
Eri kuukaudet voivat olla eri pylväsdiagrammeissa.
Pylväät voivat olla myös vaakasuunnassa.
Jos pylväsdiagrammi on piirretty vain yhdestä kuukaudesta, voi saada ensimmäisen ja viimeisen rivin pisteet.
Pylväsdiagrammin sijaan muu järkevä diagrammi (esimerkiksi viivadiagrammi), -1 p.
Alapuoleisessa esimerkissä pylväsdiagrammissa x-akselilla on päivämäärä juoksevalla numeroinnilla niin, että ensimmäinen päivä on 1.9. ja viimeinen päivä (91. päivä) on 30.11. Kuvasta ja selityksestä yhteensä 4 p.
Diagrammi: Ilman lämpötila
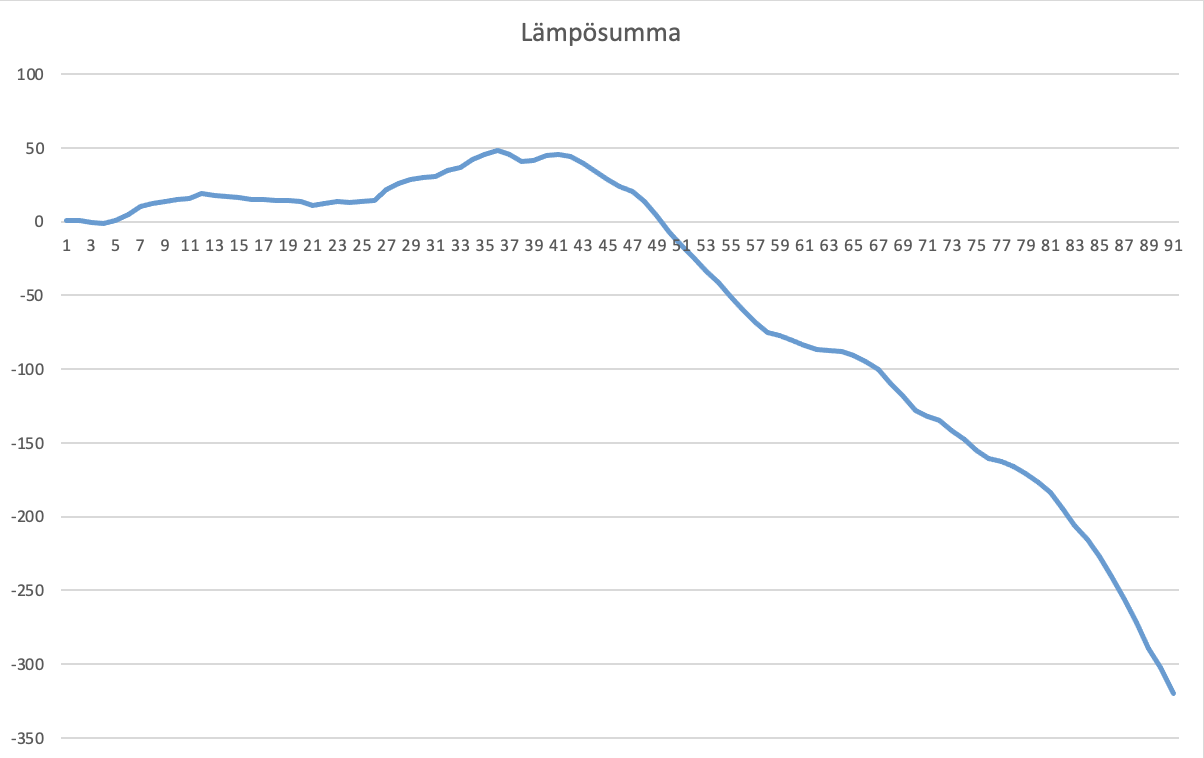
10.3.2 Määritä lämpösumman avulla, milloin terminen talvi alkoi Saanalla vuonna 2021. 10 p.
Laskettu vähintään yksi epätriviaali lämpösumma oikein / lämpösummasarakkeen toinen ja kolmas summa ovat oikein / lämpösummasarakkeen kaikki summat ovat oikein. (Ensimmäiset lämpösummat: 0,5; 0,7; -0,4; -1,2; 0,6; 5,2; 10,2; 12,4; 13,8; 14,8; 15,9.) Viimeiset kaksi pistettä saa automaattisesti, jos näkyvissä arvoissa ei ole virheitä ja seuraavan pisterivin dokumentaatio on kunnossa.
TAI
Piirretty lämpösumman kuvaaja (oikein tai väärin) / lämpösumman kuvaajan toinen ja kolmas päivä ovat oikein / lämpösumman kuvaaja on oikein. 		1+1+2 p.
Diagrammi: Lämpösumma
Dokumentaatio lämpösummasarakkeen tai lämpösumman kuvaajan muodostamisesta esitetty. Riittävä dokumentaatio sarakkeelle on esimerkiksi lämpösummasarakkeen ensimmäinen solu oikein ja summalausekkeen näkyminen kuvakaappauksessa yhdestä solusta. 		1 p.
Lämpösummasarakkeesta näkee, että suurin arvo on 48\mathrm{,}4 astetta TAI MAX-komennolla saadaan lämpösumman suurimmaksi arvoksi 48\mathrm{,}4 astetta TAI lämpösumman kuvaajasta näkee, milloin suurin arvo saavutetaan. (arvo sekä perustelu) 2 p.
Lämpösumman suurin arvo saavutettiin 6.10. 1 p.
Talvi alkoi siis melko täsmälleen 7.10. 2 p.
Osatehtäväkohtaiset erillisohjeet
Toiseksi viimeisen rivin pisteeseen kelpaa oikean päivämäärän löytäminen omista luvuista.
Systemaattinen pieni virhe lämpösumman laskemisessa: -1 ensimmäiseltä riviltä ja -1 viimeiseltä riviltä.
Joko 48,4 tai 6.10. puuttuu täysin, eikä ole edes mitenkään implikoitu, mutta toinen löytyy, viimeiseltä kolmelta riviltä max(0+1+2/2+0+2).
Sekä 48,4 että 6.10. puuttuu täysin, eikä ole edes mitenkään implikoitu. Viimeiseltä kolmelta riviltä (0+0+0).

11. Suhteellinen vaalitapa 18 p.

Kuvitteellisessa Keski-Maan vaalipiirissä on neljä puoluetta: Hobittipuolue, Ihmispuolue, Haltiapuolue ja Kääpiöpuolue. Taulukossa 11.A on esitetty Keski-Maassa toimitetun vaalin äänestystulokset.

Vastaa seuraaviin kysymyksiin olettaen, että Keski-Maassa käytetään d'Hondtin suhteellista vaalitapaa, joka on kuvattu tekstissä 11.B.

  1. Mikä oli vaalien äänestysprosentti, kun Keski-Maassa on 290 754 äänioikeutettua? (3 p.)

  2. Laske kunkin ehdokkaan vertausluku. Ketkä tulevat valituiksi, kun vaalipiiristä valitaan viisi edustajaa? (5 p.)

  3. Kuinka monta henkilökohtaista ääntä enemmän Pippinin olisi pitänyt saada, jotta hän olisi tullut valituksi ilman arvontaa? Oletetaan, että muiden äänimäärät eivät muutu. (5 p.)

  4. Suhteellisen vaalitavan tavoite on, että edustajien paikat jakautuvat samassa suhteessa kuin puolueiden saamat äänet. Pohdi, kuinka hyvin tämä toteutui näissä vaaleissa. (5 p.)

Annettu kokonaisäänimäärä 173465. 1 p.
Oma äänimäärä (väliltä 1–290753) jaettu luvulla 290754. 1 p.
riippumaton Äänestysprosentti on 60 % tai 59,7 % tai 59,66 % (ei muita tarkkuuksia) TAI oma osamäärä prosenteiksi muutettuna edellä mainitulla tarkkuudella. 1 p.
Ilmoitettu puoluekohtaiset äänimäärät (voivat olla myös muissa osatehtävissä). 1 p.
Määritetty ehdokkaiden vertausluvut (yhdessä puolueessa vähintään kolme vertauslukua oikein 1 p., kaikki loput vertausluvut oikein 1 p., perustelu luvuille: vähintään yksi lasku/sanallinen selitys 1 p.). 1+1+1 p.
Jokaisesta puolueesta valitsematta jääneistä eniten ääniä saaneen vertausluku on näkyvissä ja valittu ne 5 ehdokasta, joiden vertausluvut ovat suurimmat omilla luvuilla laskettuna. 1 p.
Osatehtäväkohtaiset erillisohjeet
Vertausluvut voi antaa yhden äänen tarkkuudella tai tarkemmin. Pyöristämisen sijaan katkaisu -0 p.
Jos vertausluku on annettu 10 tarkkuudella, niin osatehtävän pisteet max 4 p.
Äänimäärät ja vertausluvut erillisessä taulukossa.
STOP: Jos vertausluvut on laskettu täysin väärällä periaatteella, niin osatehtävistä 11.3–11.4 annetaan korkeintaan yksi alkupiste osatehtävässä 11.4, jos se on ansaittu käyttämättä virheellisiä vertauslukuja.
Pippin pääsisi läpi, jos hän saisi enemmän ääniä kuin Sam. Tämä tarkoittaisi, että hän saisi 11029-8867+1=2163 ääntä enemmän. 1+1 p.
ylläolevista riveistä riippumaton piste Pippin pääsisi läpi, jos Hobittipuolueesta tulisi valituksi kolmaskin ehdokas. Hobittipuolue tarvitsisi siis enemmän ääniä kuin Ihmispuolue. 1 p.
Tähän vaadittaisiin 65870-64038+1=1833 ääntä TAI laskettu (64038+x)/3>21956\mathrm{,}666\dots eli x>1832 (tässä hyväksytään osatehtävässä 11.2 laskettu vertausluku), joten vaaditaan 1833 ääntä. 1 p.
Verrattu kahden tapauksen oikealla periaatteella laskettuja omia äänimääriä ja vedetty oikea johtopäätös. 1 p.
Osatehtäväkohtaiset erillisohjeet
Jos molemmista laskuista puuttuu +1 ääni, niin osatehtävän pisteet max 4 p.
riippumaton Laskettu jonkin puolueen tai blokin ääniosuus ja puolueesta valittujen henkilöiden osuus kaikista valituista. Lisäksi vedetty edellisestä oikea johtopäätös. 1+1 p.
riippumaton Toinen vastaavasti perusteltu johtopäätös. Jos muiden järkevien havaintojen joukossa on selvästi virheellisiä vastauksia, niin -1 p. tältä riviltä. 2 p.
Valitut esimerkit sisältävät tapauksen, että ääniosuus vastaa edustajien osuutta, ja tapauksen, että ääniosuus ei vastaa edustajien osuutta. 1 p.
Osatehtäväkohtaiset erillisohjeet
Jos on tehty aikaisemmin laskuvirhe, voi tästä kohdasta saada max 5 omilla luvuilla.
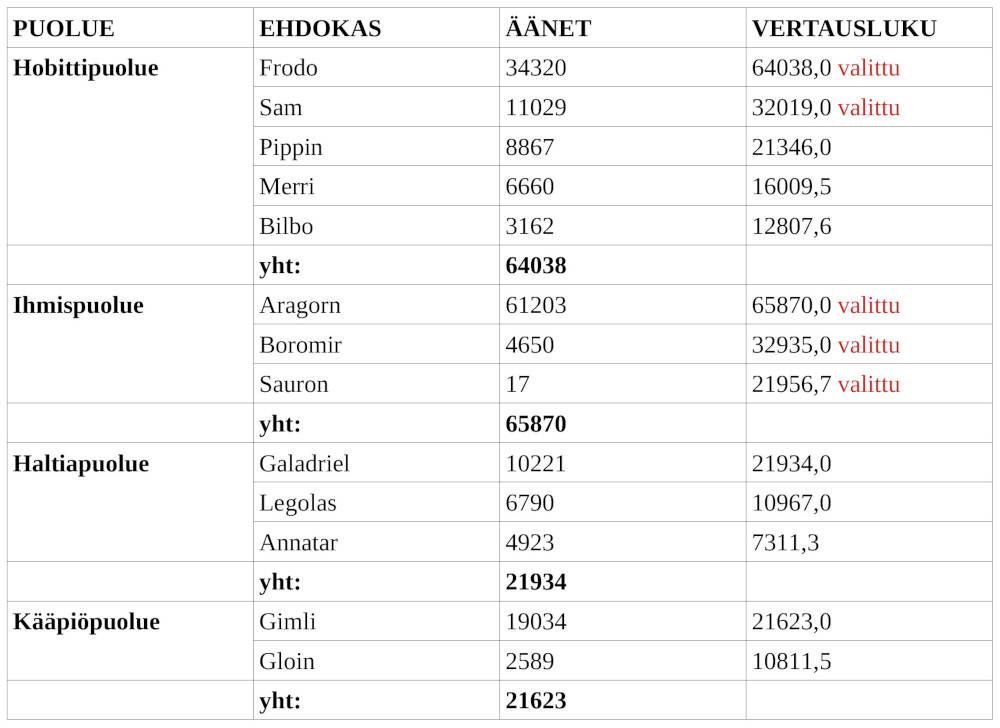Taulukko: Oikeat luvut sisältävä taulukko