Beskrivningar av goda svar: SV – Matematik, kort lärokurs
26.9.2024
Slutgiltiga beskrivningar av goda svar 14.11.2024
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal i den högra kolumnen för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i parentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- Om inget annat anges, godkänns även en gällande siffra fler eller färre än i anvisningarna.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Ordet STOP betyder att raden beskriver villkor som måste uppfyllas för att kunna få poäng för den fortsatta lösningen.
- Terminologi
- ''Svar räcker'' betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- ''Startpoäng'' betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- ''maxN'' betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- ''Svaret endast som närmevärde'' betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (t.ex. noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (t.ex. e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (t.ex. e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (t.ex. x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (t.ex. parenteser som fattas men korrekt beräknat; =-tecknet använt ''i kedja'', m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Del A
1. Vardagsmatematik 12 p.
1.1 Beräkna. 2 p.
- 14 (2 p.)
1.2 Beräkna. 2 p.
1.2.1 1 p.
- 5 (1 p.)
1.2.2 1 p.
- 37 (1 p.)
1.3 Beräkna. 2 p.
- 40 (2 p.)
- 36 (1 p.)
1.4 Beräkna. 3 p.
- 2814 (3 p.)
- 2905 (1 p.)
1.5 Beräkna. 3 p.
- 7 (3 p.)
- -7 (2 p.)
- 401 (1 p.)
- 67 (1 p.)
- 19 (1 p.)
401: Tänkt hela vattenåtgången som den månatliga åtgången. (1 p.)
67: Räknat vattenåtgången korrekt, men tänkt 12 euro som en engångssumma. (1 p.)
19: Räknat ihop sista förskottsavgiften och utjämningen till samma räkning. (1 p.)
2. Ekvation och triangel 12 p.
Lös ekvationen x^2+14=9x. (4 p.)
Linjen y=-2x+6 avgränsar tillsammans med de positiva x- och y-axlarna en rätvinklig triangel. Bestäm triangelns area samt hypotenusans längd. (8 p.)
| Skrivit om på formen x^2-9x+14=0 (ordningen av termerna i vänsterledet är oväsentlig). Detta poäng fås även utan mellanled, om alla koefficienter är rätt insatta i lösningsformeln. | 1 p. |
| Satt in koefficienterna 1, -9 och 14 i lösningsformeln, möjligen på fel plats och med fel tecken. | 1 p. |
| Alla koefficienter korrekt insatta i lösningsformeln x=\frac{9\pm \sqrt{(-9)^2-4\cdot 14}}{2} ELLER bifogat en skärmdump av Speedcrunch, där de använda koefficienterna framgår. | 1 p. |
| STOP: Insättningen innehåller högst ett teckenfel och beräknat två olika rötter korrekt från den egna formeln (x=2 och x=7). | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Testlösning: 1 p. per korrekt insättning och uträkning. | |
| b och c förväxlade i lösningsformeln, max(1+1+0+0). | max 2 p. |
| Ett teckenfel i insättningen, max(1+1+0+1). | max 3 p. |
| Litet fel i omskrivningen av ekvationen, max(0+1+1+1). | max 3 p. |
| Exempel som ger (1+1+0+1): skrivit -9^2 som beräknats till rätt värde 81 och fått nollställena 2 och 7; som första term i täljaren i stället för 9 skrivit -9 och fått nollställena -2 och -7. | |
| Exempel som ger max(1+1+0+0): skrivit -9^2 som beräknats till -81, varför argumentet till kvadratroten är negativ. |
| Kateten k_1=6 (ty linjen skär y-axeln i punkten y=6). | 2 p. |
| Kateten k_2=3 + förklaring: linjen skär x-axeln då -2x+6=0. | 1+1 p. |
| STOP: Om hittills 0 p. så kan man inte få poäng för fortsättningen. | |
| Satt in egna positiva kateter i formeln \frac{k_1\cdot k_2}{2} / ganska exakt fått 9. | 1+1 p. |
| Satt in egna kateter i formeln \sqrt{k_1^2+k_2^2} / ganska exakt fått \sqrt{45} eller 6{,}7 eller noggrannare. | 1+1 p. |
| Särskilda anvisningar för deluppgiften | |
| Om första radens katet är på x-axeln så -1 p. Annars ger endast svar fulla poäng från första raden. | |
| Om kateterna framgår implicit först vid insättning i formlerna, så max(1+1+2+2). | |
| Som förklaring i rad 2 räcker inte en bild där en linje dragits genom punkterna (0, 6) och (3, 0), där det inte framgår hur linjen ritats. En skiss av linjen kan förklaras exempelvis med en tabell eller med riktningskoefficienten (1 längdenhet åt höger och 2 nedåt). | |
| Kvadratroten behöver inte föregås av \pm. | |
| Exempel på fallet (2+0+1+1): Fått kateternas längder 6 och 2 (ty 2x), beräknat arean \frac{6 \cdot 2}{2} = 6 och hypotenusans längd \sqrt{6^2 + 2^2} \approx 6{,}3. |
3. Dricksglas i en reklam 12 p.
En reklambyrå planerar en reklamvideo för ett maskindiskmedel. Producentens tanke är att placera ett stort antal dricksglas i ett triangulärt mönster enligt bild . Första raden består av ett glas, andra raden av två glas, tredje raden av tre glas och så vidare, så att en rad alltid har ett glas mera än den föregående raden.
Hur många glas finns det totalt i de tio första glasraderna? (3 p.)
Ange ett uttryck för det totala antalet glas då glasraderna är n till antalet. (4 p.)
Hur många glasrader finns det i ett mönster som består av 3\,916 glas? (5 p.)
| 1+2+3+\cdots +10=55 ELLER \frac{10(10+1)}2 ELLER förklaring i ord ELLER bra bild. | 2 p. |
| oberoende Som svar ganska exakt 55. | 1 p. |
| Nämnt aritmetisk följd eller summa, eller formeln a_n=a_1+(n-1)d, eller formeln S_n=n\frac{a_1+a_n}2. | (1 p.) |
| Insett a_1 =1 och a_n=n. Även formen a_n=1+(n-1)\cdot 1 eller liknande godkänns. | 1 p. |
| Rätt svar ganska exakt n\frac{(1+n)}{2}. | 1 p. |
| Motivering med hjälp av formeln för aritmetisk summa eller den allmänna formeln S_n=n\frac{a_1+a_n}2. Det förutsätts att motiveringen konkret anknyts till situationen som beskrivs i uppgiften. | 1 p. |
| Särskilda anvisningar för deluppgiften | 1 p. |
| Endast svar. | 0 p. |
| Poäng från de två första raderna kan man få från de övriga deluppgifterna. |
| Bildat ekvationen \frac{n(n+1)}{2}=3916. | 1 p. |
| Fått en andragradsekvation n^2+n-7832=0. | 1 p. |
| Satt in koefficienterna från den egna andragradsekvationen i lösningsformeln eller i SpeedCrunch. | 1 p. |
| Fått en positiv och en negativ heltalslösning som är korrekta för den egna ekvationen. (n=88 eller n=-89) | 1 p. |
| oberoende Som svar ganska exakt 88. | 1 p. |
| Särskilda anvisningar för denna lösning | |
| Fel i förenklingen, men som svar valt ett naturligt tal som fåtts som lösning till ekvationen (1+0+1+1+0). | max 3 p. |
| ELLER (testlösning) | |
| Beräknat 1+2+3+\dots+88 ELLER motsvarande tabellering 1, \ldots, 88 ELLER \frac{n(n+1)}2=3916 ELLER 88\cdot\frac{88+1}{2}. | 1 p. |
| Fått från beräkningar eller tabell 3916 ELLER testat att 88 är en lösning till ekvationen ELLER noterat att 88\cdot\frac{88+1}2 = 3916. | 2 p. |
| Noterat att det inte finns andra lösningar, eftersom antalet glas växer. | 1 p. |
| oberoende Som svar ganska exakt 88. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Använt en felaktigt motiverad men korrekt formel \frac{n(n+1)}2 från deluppgift 3.2. | max 5 p. |
| Använt en felaktig formel från deluppgift 3.2, som leder till en andragradsekvation. | max 4 p. |
| Använt en felaktig formel från deluppgift 3.2, som inte leder till en andragradsekvation. (1+0+0+0). | max 1 p. |
4. Kulstötning 12 p.
Utifrån det toppresultat som Ryan Crouser stötte 18.2.2023 har man gjort en modell för en kulstöts resultat i meter med polynomfunktionen
f(x)=-0{,}0126x^2+1{,}07x+0{,}630,
då variabeln 0\le x\le 60 är stötens riktningsvinkel i grader (mätt från horisontalplanet). Bestäm genom att använda derivatan den stötvinkel som leder till det största stötresultatet med en noggrannhet på en hundradels grad och det motsvarande stötresultatet med en centimeters noggrannhet.
| Funktionens derivata är f'(x)=2\cdot (-0\mathrm{,}0126)x+1\mathrm{,}07\,(=-0\mathrm{,}0252x+1\mathrm{,}07). (konkret försök att beräkna derivatan 1 p., graden av derivatan korrekt 1 p. och 1 p./korrekt term) | 4 p. |
| STOP: Inga poäng för resten om derivatan inte är ett förstagradspolynom. | |
| Derivatans nollställe är x\approx 42\mathrm{,}46. (f'(x)=0, eller nämnt derivatans nollställe 1 p., en hundradels noggrannhet 1 p.) | 2 p. |
| oberoende Det största värdet finns antingen i intervallets ändpunkter eller i derivatans nollställe (inom intervallet). (Nämnt att det största värdet finns antingen i intervallets ändpunkter eller i derivatans nollställe (inom intervallet) 1 p., beräknat funktionens värden f(0)=0{,}63 \text{ och } f(60)=19{,}47 i intervallets ändpunkter 1 p.) ELLER Eftersom funktionsgrafen är en parabel som öppnar sig nedåt, har den ett största värde i derivatans nollställe. ELLER Studerat derivatans tecken på båda sidor om nollstället och visat exempelvis med teckenschema att funktionen har ett maximum i derivatans nollställe. (Försök med teckenschema 1 p.) | 2 p. |
| Eftersom derivatans nollställe 42,46 ligger inom det givna intervallet [0, 60], så är det största värdet ungefär f(42{,}46)\approx 23{,}35 \text{ m}. (Noterat att nollstället ligger i det givna intervallet [0, 60]. Detta kan framgå även av ett teckenschema där intervallets ändpunkter ingår. 1 p., beräknat funktionsvärdet i derivatans nollställen 1 p., en centimeters noggrannhet 1 p., enhet 1 p.) | 4 p. |
| Särskilda anvisningar för deluppgiften | |
| Från sista raden kan man få alla poäng, så länge lösningen fram dit fortskridit på ett logiskt sätt och man kommit förbi stop-regeln, även om man gjort räknefel. | |
| Nollstället till den egna derivatan ligger utanför intervallet [0,60] och som svar gett största värdet i intervallets ändpunkt: sista raden ger max(1+1+1+1). | |
| Nollstället till derivatan kan ges med två decimalers noggrannhet för full poäng, mellanleden behöver inte ha större noggrannhet. | |
| Bestämt maxpunkten utan derivata (exempelvis med intervallhalvering). | 0 p. |
| Bestämt derivatans nollställe med intervallhalvering utan att motivera entydighet. | max 11 p. |
| Rad 1 och 2 följt av endast f(42{,}46)\approx 23{,}35. (4+2+0+2) |
5. Jämförelse av lån 12 p.
Nanny och Simon tar varsitt lån på 9 000 euro. Nannys lån är ett lån med jämn amortering och Simons lån är ett annuitetslån. Den årliga räntesatsen på båda lånen är 5 % och lånetiden är 3 år. De amorterar sina lån en gång per år. Vems sista betalningsrat är störst?
| oberoende Räntekoefficient 1+\frac{5}{100} eller 1\mathrm{,}05, eller ränta 0\mathrm{,}05. | 1 p. |
| Använt annuitetsformeln med sin egen räntekoefficient q ( 9000\cdot 1\mathrm{,}05^3\cdot \frac{1-1\mathrm{,}05}{1-1\mathrm{,}05^3} ) (q>1 och insättning i rätt formel 1 p. / räntekoefficienten svarar mot antalet betalningsrater 1 p. / 9000 som en faktor 1 p.). | 3 p. |
| Resultatet av annuitetsformeln tillhör intervallet (\frac{9000}{n}, 9000) och svarat med sista/varje betalningsrats storlek (3304\mathrm{,}88). Här betecknar n antalet betalningsrater.) | 1 p. |
| poäng oberoende av de ovanstående raderna Påpekat att med jämn amortering är alla amorteringar lika stora. | (1 p.) |
| Beräknat amorteringen med formeln \frac{9000}{n} / resultat (\frac{9000}{3}=3000). | 2 p. |
| Den sista betalningsratens storlek är beräknad enligt rätt princip från de egna talen (3000\cdot 1{,}05=3150 ELLER 3000\cdot 0{,}05=150 / 3000+150=3150). | 2 p. |
| Talen exakt 3304{,}88 och 3150{,}00, och enligt jämförelsen är sista raten större för Simon / med annuitetslån / mindre för Nanny / med jämn amortering (båda talen korrekta 1 p. Slutsats: jämförelse och slutsats 1 p.). | 2 p. |
| Särskilda anvisningar för denna lösning | |
| Mellanavrundning ok, noggrannhet minst 2 gällande siffror. | |
| Månadsamorteringar (q=1\mathrm{,}004167, antal rater: 36, jämförelse 268\mathrm{,}74>251\mathrm{,}04). (0+3+1+1+2+2+0). | max 9 p. |
| Räntekoefficient q=1\mathrm{,}005 eller q=1\mathrm{,}0005 (0+3+1+1+2+2+0). | max 9 p. |
| Räntekoefficient q=0\mathrm{,}05 (0+1+0+1+2+2+0). | max 6 p. |
| Olika räntor eller räntekoefficienter använda för de två lånen, varav den ena är korrekt. (1+2+1+1+2+2+0) ELLER (1+3+1+1+2+1+0) | max 9 p. |
| Exempelvis för lånet med jämn amortering räknat \frac13 \cdot (1{,}05 \cdot 9000) = 3150 eller 9450 i mellanledet: från rad 4–6 (0+1+2). Om man dessutom skrivit ''i ett lån med jämn amortering är alla amorteringar lika stora'', så (1+1+2). | max 8–9 p. |
| Exempelvis beräknat utan förklaring 9000/3=3000 och 1{,}05\cdot 3000=3150. Från rad 4–6 (1+2+2) och -1 p. för bristande motivering. Inga poäng från sista raden. | max 9 p. |
| ELLER | |
| I ett lån med jämn amortering minskar raterna och i ett annuitetslån är alla rater samma. | 1 p. |
| Om den sista betalningsraten i annuitetslånet vore mindre än (eller lika med) sista raten för lånet med jämn amortering, så vore alla rater i annuitetslånet mindre (eller lika med, för den sista raten) än för lånet med jämn amortering. | 5 p. |
| Eftersom båda lånen har samma ränta, kan annuitetslånets rater inte räcka till / man skulle betala för mycket i lånet med jämn ränta. (Om den sista betalningsraten i annuitetslånet vore mindre än eller lika med sista raten 1{,}05 \cdot 3000 euro för lånet med jämn amortering, så vore alla rater i annuitetslånet mindre eller lika med detta tal. Då skulle man för annuitetslånet betala < 1{,}05 \cdot 9000 euro, vilket inte är möjligt med 5 % årsränta och årliga rater.) | 4 p. |
| Slutsats: Därför är den sista raten större för annuitetslånet (Simons lån). | 2 p. |
6. Fördelningar, grafer och sannolikheter 12 p.
Välj korrekt alternativ. Svaren behöver inte motiveras. Korrekt svar 2–3 p., fel svar 0 p., inget svar 0 p.
Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning kan du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
6.1 Kombinera följande påståenden med den lämpliga fördelningen för sannolikheten för att lyckas i figur . Vi kastar två tärningar en gång och målet är att 6 p.
6.1.1 2 p.
- Fördelning 1 (2 p.)
6.1.2 2 p.
- Fördelning 3 (2 p.)
6.1.3 2 p.
- Fördelning 4 (2 p.)
6.2 En kortlek har fyra färger, och varje färg utgörs av kort med talen 2–10. Två kort tas ur kortleken utan återläggning. 6 p.
6.2.1 3 p.
- inget av ovanstående (3 p.)
6.2.2 3 p.
- \frac{17}{21} (3 p.)
Del B
7. Pepparkaksburkar 12 p.
Julens pepparkakor förpackas i tre olika stora plåtburkar med cirkelformade bottnar. Dessa visas i bild .
Den största burkens omkrets är 78,5 cm och höjden är 10,0 cm.
Den mellersta burkens radie är 1,5 cm mindre och höjden är 1,0 cm mindre än motsvarande mått på den större burken.
Den minsta burkens radie är 2,5 cm mindre och höjden är 1,0 cm mindre än motsvarande mått på den mellersta burken.
Beräkna burkarnas sammanlagda volym med en deciliters noggrannhet.
| Beräknat diametern av den största burken 78{,}5/\pi \approx 24{,}99. | (1 p.) |
| Skrivit radien enligt formeln 78{,}5/(2\pi) ELLER formulerat ekvationen 78{,}5=2\pi r. | 1 p. |
| poäng oberoende av de ovanstående raderna Radien är ganska exakt 12{,}49\approx 12{,}5 (eller noggrannare). | 1 p. |
| STOP: Poäng från denna rad fås endast om den stora burkens radie framtagits på rätt sätt. Beräknat radierna av de två mindre burkarna genom att subtrahera 1,5 och 4 från den stora burkens radie. (korrekta resultat10{,}99 och 8{,}49 eller 11 och 8{,}5). | 1+1 p. |
| poäng oberoende av de ovanstående raderna Höjden av de två mindre burkarna 9{,}0 och 8{,}0 (eller 9 och 8). | 1 p. |
| Beräknat volymen med rätt formel och de egna talen korrekt insatta (\pi (12{,}49)^2 \cdot 10{,}0, \pi (10{,}99)^2 \cdot 9{,}0 och \pi (8{,}49)^2 \cdot 8{,}0). Radierna och höjderna i samma enhet eller enheterna utskrivna, annars 0 p. | 1 p. |
| Cylinderns volym beräknad från tal med rätt enhet eller volymenheten korrekt och utskriven i räkningarna eller senare. | 1 p. |
| STOP: Poäng från följande rader fås endast om cylinderns volym och volymenhet korrekta och utskrivna i räkningarna eller senare. | |
| Summan av volymerna (4903{,}763+3417{,}254+1813{,}134 = 10134{,}151~\text{cm}^3). Gjort korrekt enhetsomvandling till deciliter eller liter. Av presentationen bör framgå mellan vilka enheter som omvandlingen skett, annars 0 p. | 1+2 p. |
| Summan beräknad, enhetsomvandlingen korrekt och svaret givet med en deciliters noggrannhet (101 (dl) eller 10{,}1 l, eller i annan enhet med förklaring varför noggrannheten är korrekt). | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Rad 4 och 8 kräver inga formler för beräkningarna, såvida resultaten kan tolkas tydligt från formler eller förklaringar. | |
| Om rad 6 innehåller korrekt formel och korrekt utförda insättningar, men man har gjort ett räknefel i volymberäkningen, fås poäng för rad 6, men förlorar poäng för volymernas summa i rad 8. | |
| Använt diameter (i stället för radie) genom hela räkningen inklusive volymberäkningen, så att exempelvis rad 5 blir \pi(24{,}99)^2 \cdot 10{,}0 (1+0+0+0+1+1+1+3+1). | max 8 p. |
| Tolkat uppgiften så att 1{,}5 och 4 är skillnaderna av diametrarna i stället för av radierna, i övrigt rätt (alla poäng utom rad 4). | max 10 p. |
| En lösning med programvara bör innehålla samma mellanled. Dessutom bör beräkningar och kommandom vara synliga. Om exempelvis radien är bestämd tillräckligt noggrannt genom test, fås från de första raderna (0+0+1+\ldots). |
8. Kostnader för en motorväg 12 p.
Tidningen Helsingin Sanomat skrev 20.6.1972:
I ett vägprojekt som slutfördes 2018 blev kostnaden för en 32 kilometer lång motorvägssträcka från Fredrikshamn till Vaalimaa 550 miljoner euro. I den här uppgiften jämförs kostnaderna de olika åren genom att använda ett "Kalle Anka-index", som baseras på följande information: Ett lösnummer av tidningen Kalle Anka kostade 0,80 mark år 1972 och 3,50 euro år 2018.
Vad kostade motorvägen Helsingfors-Lahtis i 2018 års penningvärde?
Hur många procent dyrare var motorvägen Fredrikshamn-Vaalimaa än motorvägen från Helsingfors till Lahtis per kilometer om man beaktar förändringen i pengarnas värde?
| Kostnaden för motorvägen Helsingfors–Lahtis i dagens penningvärde: | |
| Baserat på priset för Kalle Anka kan man uppskatta att penningvärdet har förändrats ungefär med koefficienten \frac{3\mathrm{,}50}{0\mathrm{,}80}\, (\frac{\textrm{euro}}{\textrm{mk}})=4\mathrm{,}375\, (\frac{\textrm{euro}}{\textrm{mk}}) ELLER kvoten \frac{0\mathrm{,}80}{3\mathrm{,}50}\, (\frac{\textrm{mk}}{\textrm{euro}})=0\mathrm{,}22857142857\ldots (\frac{\textrm{mk}}{\textrm{euro}}) ELLER formulera förhållandeekvationen \frac{0\mathrm{,}80}{3\mathrm{,}50}=\frac{320}{x}. | 2 p. |
| Studenten har förstått jämförelsen av valutaförändringen korrekt (exempelvis med tabell eller förhållandeekvation eller med koefficient). | 1 p. |
| Kostnaderna var alltså 320\cdot 4\mathrm{,}375 ELLER 320:0\mathrm{,}22857142857 ELLER 320\cdot \frac{3\mathrm{,}50}{0\mathrm{,}80} | 2 p. |
| = ganska exakt 1400 miljoner euro. | 1 p. |
| Jämförelse av kostnaderna: | |
| Baserat på 2018 års penningvärde | |
| Fredrikshamn–Vaalimaa kostade \frac{550\,000\,000}{32}=17187500 euro per kilometer. | 2 p. |
| poäng oberoende av de ovanstående raderna Helsingfors–Lahtis kostade 3\cdot 10^6\cdot 4\mathrm{,}375 \, (\frac{\textrm{euro}}{\textrm{km}}) (=13\,125\,000 \,(\frac{\textrm{euro}}{\textrm{km}})). (kilometerpriset 1 p. och omvandling från mark till euro 1 p.) | 2 p. |
| Beräknat jämförelseprocenten enligt rätt princip (exempelvis \frac{17\,187\,500-13\,125\,000}{13\,125\,000}). | 1 p. |
| Den nya motorvägen är alltså ungefär exakt 31 % dyrare än den gamla. | 1 p. |
| Beräknat längden och kilometerpriset av motorvägen Helsingfors–Lahtis med hjälp av informationen 3 mk/mm. | |
| Fredrikshamn–Vaalimaa kostade \frac{550\,000\,000}{32}=17\,187\,500 euro per kilometer. | 2 p. |
| poäng oberoende av de ovanstående raderna Beräknat längden av motorvägen Helsingfors–Lahtis enligt rätt princip: \frac{320 \cdot 10^6\, (\textrm{mk})}{3 (\frac{\textrm{mk}}{\textrm{mm}})}\, (= \frac{320}{3} (\textrm{km}) \approx 106\mathrm{,}666\ldots (\mathrm{km})). | 1 p. |
| Beräknat priset av motorvägen Helsingfors–Lahtis enligt rätt princip: \frac{1\,400\,000\,000(\textrm{euro})}{\frac{320}{3}(\textrm{km})}\,(=13\,125\,000 (\frac{\textrm{euro}}{\text{km}})). | 1 p. |
| Beräknat jämförelseprocenten enligt rätt princip (exempelvis \frac{17\,187\,500-13,125\,000}{13\,125\,000}). | 1 p. |
| Den nya motorvägen är alltså ungefär exakt 31 % dyrare än den gamla. | 1 p. |
| Baserat på 1972 års penningvärde | |
| Fredrikshamn–Vaalimaa kostade \frac{550\,000\,000}{32}=17\,187\,500 euro per kilometer. | 2 p. |
| Beräknat kostnaden per kilometer för Fredrikshamn–Vaalimaa i 1972 års penningvärde enligt rätt princip: 17\,187\,500 \cdot \frac{8}{35}=\frac{27\,500\,000}{7}\approx 3\,928\,571\mathrm{,}42 mark. | 1 p. |
| poäng oberoende av de ovanstående raderna Helsingfors–Lahtis kostade 3 \,(\frac{\textrm{mk}}{\textrm{mm}})= 3 \cdot 10^6 \,(\frac{\textrm{mk}}{\textrm{km}}) = 3 miljoner mark per kilometer. | 1 p. |
| Beräknat jämförelseprocenten enligt rätt princip: \frac{\frac{27\,500\,000}{7}-3\cdot 10^6}{3\cdot 10^6}. | 1 p. |
| Den nya motorvägen är alltså ungefär exakt 31 % dyrare än den gamla. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Med uttrycket ''Beräknat jämförelseprocenten enligt rätt princip'' menas, i fallet där kostnaden delas på längden, att värdena ges i samma enhet och jämförs med den gamla kostnaden. |
9. En motiverad binomialfördelning 12 p.
En tärning kastas sex gånger. Sannolikheten för att få ögontalet 6 exakt fyra gånger är enligt formeln för binomialsannolikhet
{6 \choose 4} \big(\tfrac16\big)^4 \big(\tfrac56\big)^2 = \frac{125}{15552} \approx 0{,}00804.
Förklara den använda formeln och alla de delar som förekommer i den, det vill säga motivera formeln för binomialsannolikhet i denna situation.
| Förklarat sannolikheten för en vilken som helst följd av kast | |
| 1/6 är sannolikheten att få en sexa med ett kast. | 1 p. |
| (1/6)^4 är sannolikheten att få en sexa fyra gånger. | 2 p. |
| 5/6 är sannolikheten att få något annat än en sexa med ett kast. | 1 p. |
| (5/6)^2 är sannolikheten att få något annat än en sexa två gånger. | 2 p. |
| Sannolikheterna (1/6)^4 och (5/6)^2 multipliceras med varandra, för vi vill beräkna sannolikheten att de båda inträffar samtidigt. | 1 p. |
| Förklarat antalet kastföljder och totala sannolikheter | |
| Binomialkoefficienten \binom{6}{4} talar om hur många gynnsamma kastföljder det finns. | 2 p. |
| Förklarat betydelsen av talen 6 och 4 i binomialkoefficienten. Exempelvis: det finns sex möjliga platser i följden och av dessa väljer man ut de fyra där man ska få en sexa ELLER på hur många sätt (kastföljder) kan man välja ut vilka fyra av de sex kasten som ger ögontalet sex ELLER i hur många ordningar, till exempel i en följd, kan man placera fyra sexor och två av något annat ögontal. | 1 p. |
| Påpekat att alla kastföljder är lika sannolika, eller detta framgår av lösningen (1 p.). Sannolikheten för varje enskild kastföljd multipliceras med binomialkoefficienten, för att beräkna den totala sannolikheten för alla gynnsamma kastföljder (1 p.). | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Många rader är oberoende, utan att detta är speciellt markerat. | |
| Inga poäng för att beskriva processen. Exempelvis ger ''Vi skriver 6 där uppe för att det är antalet kast och 4 där nere för att det är antalet gynnsamma fall'' inga poäng för rad 7. |
10. Termisk vinter 18 p.
Välj det korrekta alternativet i deluppgifterna 10.1–10.2. Svaren behöver inte motiveras. Korrekt svar 1–2 p., fel svar 0 p., inget svar 0 p. Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning kan du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
Vi undersöker temperaturer uppmätta vid meteorologiska stationen på Saana på tabell med hjälp av begreppen i text . Texten är en presentation om termiska årstider av Meteorologiska institutet i sin helhet. För att lösa uppgiften måste du själv hitta den information som behövs i texten.
10.1 Välj korrekt alternativ. 2 p.
10.1.1 1 p.
- 7 (1 p.)
10.1.2 1 p.
- 27.9. (1 p.)
10.2 Välj korrekt alternativ. 2 p.
- 1 (2 p.)
10.3 Skriv svaren på deluppgifterna 10.3.1 och 10.3.2 i svarsfälten. 14 p.
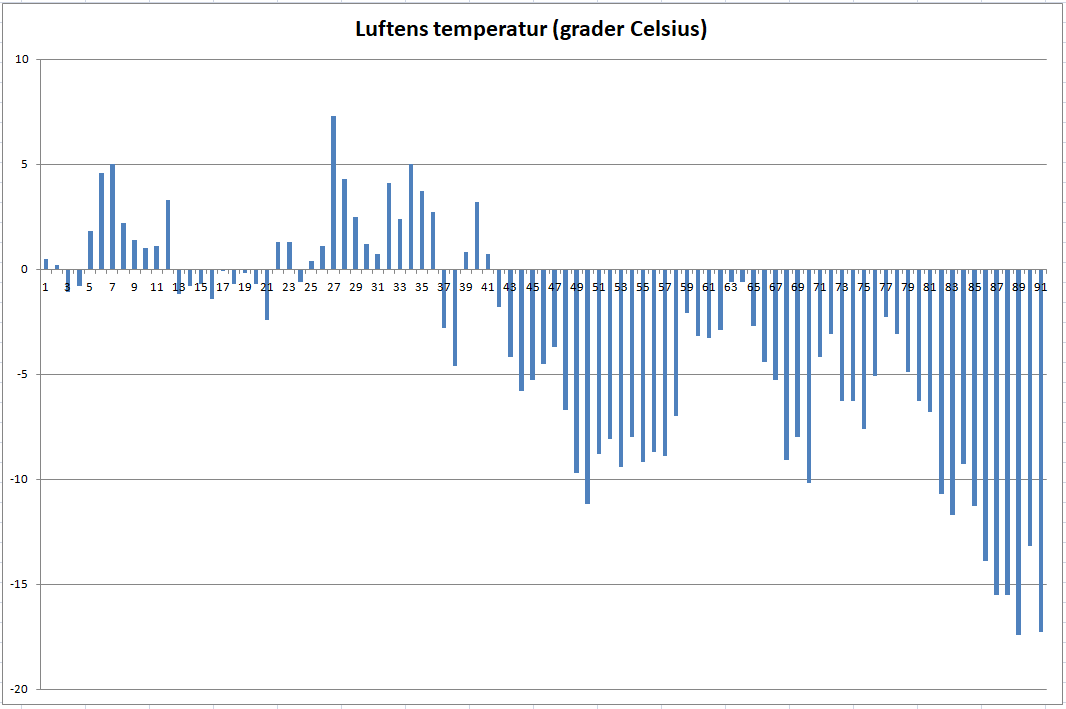
10.3.1 Rita ett stapeldiagram över de dagliga medeltemperaturerna. 4 p.
| Ritat ett stapeldiagram med minst 3 staplar, vilka svarar mot den angivna datan. | 1 p. |
| Ritat ett stapeldiagram, som innehåller alla staplar på ögonmått rätt ritade (kan också innhålla andra staplar). | 1 p. |
| Stapeldiagrammet har rätt antal staplar och alla är korrekta. | 1 p. |
| Axlarna på stapeldiagrammet markerade och tydligt förklarade. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Tredje raden ger ej poäng om det finns överflödiga staplar. | |
| Överflödiga förklaringar, till exempel ''blå färg kolumn D'' eller ''blå färg 0,5''. | –0 p. |
| Staplarna behöver inte börja från 0 grader, utan kan börja från exempelvis -20 grader. | |
| Olika månader kan vara i olika stapeldiagram. | |
| Staplarna kan också vara horisontella. | |
| Om stapeldiagrammet ritats för bara en månad, kan man få poäng för första och sista raden. | |
| I stället för stapeldiagram ett annat relevant diagram (exempelvis linjediagram), -1 p. | |
| I stapeldiagrammet i exemplet nedan är x-axeln markerad med löpande nummer så att första dagen är 1.9. och sista dagen (91. dagen) är 30.11. Bilden och förklaringen tillsammans ger 4 p. | |
 Graf: Luftens temperatur
|
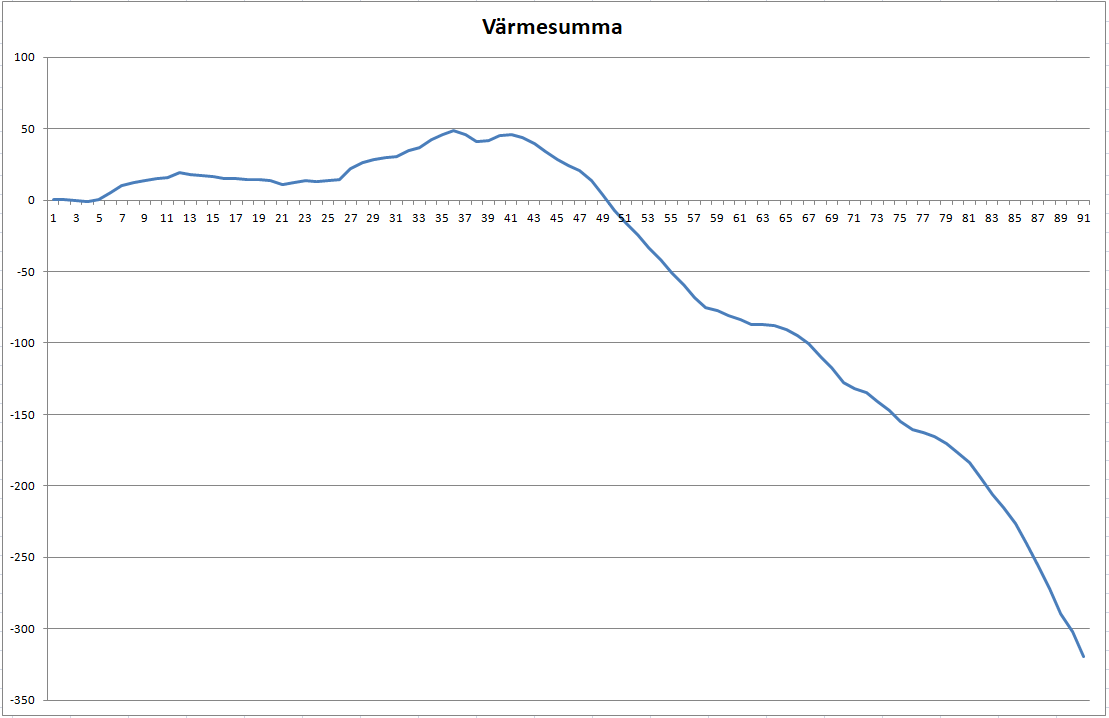
10.3.2 Bestäm med hjälp av värmesumman när den termiska vintern började på Saana år 2021. 10 p.
| Beräknat minst en icketrivial värmesumma korrekt / andra och tredje summan i värmesummakolumnen är korrekta / alla summor i värmesummakolumnen är korrekta. (De första värmesummorna: 0,5; 0,7; -0,4; -1,2; 0,6; 5,2; 10,2; 12,4; 13,8; 14,8; 15,9.) De sista två poängen fås automatiskt om det inte finns några fel i de synliga värdena och dokumentationen i följande poängrad är i ordning. ELLER Ritat en graf (korrekt eller felaktig) över värmesumman / andra och tredje summan i värmesummagrafen är korrekta / värmesummagrafen är korrekt. | 1+1+2 p. |
 Graf: VärmesummaPresenterat dokumentation över hur värmesummakolumnen eller värmesummagrafen bildats. Tillräcklig dokumentation för kolumnen är exempelvis att första cellen i kolumnen är korrekt och att summaformeln för någon annan cell syns i en skärmdump. | 1 p. |
| I värmesummakolumnen syns att största värdet är 48\mathrm{,}4 grader ELLER MAX-kommandot ger största värdet 48\mathrm{,}4 grader ELLER i värmesummagrafen syns var det största värdet antas. (värde samt förklaring) | 2 p. |
| Värmesummans största värde antogs 6.10. | 1 p. |
| Vintern började alltså ganska exakt 7.10. | 2 p. |
| Särskilda anvisningar för deluppgiften | |
| Den näst sista radens poäng kan fås om man hittat rätt datum från de egna talen. | |
| Systematiskt mindre fel då värmesumman beräknats: -1 från första raden och -1 från sista raden. | |
| Antingen 48,4 eller 6.10. saknas helt, och framgår inte ens implicit, men det andra förekommer, från de sista tre raderna max(0+1+2/2+0+2). | |
| Både 48,4 och 6.10. saknas helt, och framgår inte ens implicit. Från de sista tre raderna (0+0+0). |
11. Proportionell valmetod 18 p.
I den fiktiva valkretsen i Midgård finns fyra partier: Hobbitpartiet, Människopartiet, Alvpartiet och Dvärgpartiet. Tabell visar resultatet av valet i Midgård.
Besvara följande frågor under antagandet att man i Midgård använder d'Hondts proportionella valmetod, som beskrivs i text .
Hur högt var valdeltagandet i procent, då det i Midgård finns 290 754 röstberättigade? (3 p.)
Beräkna jämförelsetalet för varje kandidat. Vilka kommer att väljas om det från valkretsen väljs fem kandidater? (5 p.)
Hur många fler personliga röster hade Pippin behövt för att bli vald utan lottning? Vi antar att de övriga kandidaternas röstetal inte ändras. (5 p.)
Målet med den proportionella valmetoden är att kandidaternas platser fördelas i samma proportion som antalet röster partierna får. Diskutera hur väl det här uppnåddes. (5 p.)
| Givit totala antalet röster 173465. | 1 p. |
| Dividerat det egna röstantalet (i intervallet 1–290753) med 290754. | 1 p. |
| oberoende Valdeltagandet var 60 % eller 59,7 % eller 59,66 % (ingen annan noggrannhet) ELLER egen andel omvandlat till procent med noggrannheten ovan. | 1 p. |
| Angett röstantalet per parti (kan också ingå i andra deluppgifter). | 1 p. |
| Bestämt kandidaternas jämförelsetal (minst tre jämförelsetal korrekta i något parti 1 p., alla övriga jämförelsetal korrekta 1 p., förklaring till talen: minst en beräkning eller förklaring i ord 1 p.). | 1+1+1 p. |
| I varje parti syns jämförelsetalet för den kandidat som fått flest röster bland de icke valda, och de fem kandidater som har högst jämförelsetal utifrån de egna talen är valda. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Jämförelsetalen kan anges med en rösts noggrannhet eller noggrannare. Avrundning nedåt ger -0 p. | |
| Om jämförelsetalet givits med 10 rösters noggrannhet, så ges för denna deluppgift | max 4 p. |
| Röstantal och jämförelsetal i en skild tabell. | |
| STOP: Om jämförelsetalen beräknats enligt helt fel princip, så ger deluppgifterna 11.3–11.4 högst ett startpoäng för deluppgift 11.4, om det förtjänats utan att använda felaktiga jämförelsetal. |
| Pippin hade blivit vald om han hade fått fler röster än Sam. Detta betyder att han skulle få 11029-8867+1=2163 fler röster. | 1+1 p. |
| poäng oberoende av de ovanstående raderna Pippin hade blivit vald om en tredje kandidat från Hobbitpartiet hade blivit vald. Hobbitpartiet hade då behövt få fler röster än människopartiet. | 1 p. |
| Detta skulle kräva 65870-64038+1=1833 röster ELLER beräknat (64038+x)/3>21956\mathrm{,}666\dots alltså x>1832 (här godkänns jämförelsetal beräknade i deluppgift 11.2), så det krävs 1833 röster. | 1 p. |
| Jämfört de två fallen enligt egna röstantal som beräknats enligt rätt princip, och dragit rätt slutsats. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Om båda beräkningarna saknar +1 röst så ges för denna deluppgift | max 4 p. |
| oberoende Beräknat andelen röster för något parti eller något block, och andelen av alla valda personer som tillhör detta parti eller block. Dessutom dragit korrekt slutsats av ovanstående. | 1+1 p. |
| oberoende En andra slutsats dragen på motsvarande sätt. Om det bland de rimliga observationerna finns tydligt felaktiga svar, så -1 p. för denna rad. | 2 p. |
| De valda exemplena innehåller ett fall där röstandelen svarar mot andelen valda kandidater, och ett fall där röstandelen inte svarar mot andelen valda kandidater. | 1 p. |
| Särskilda anvisningar för deluppgiften | |
| Om man tidigare gjort ett räknefel, kan man från denna deluppgift få max 5 med egna tal. | |
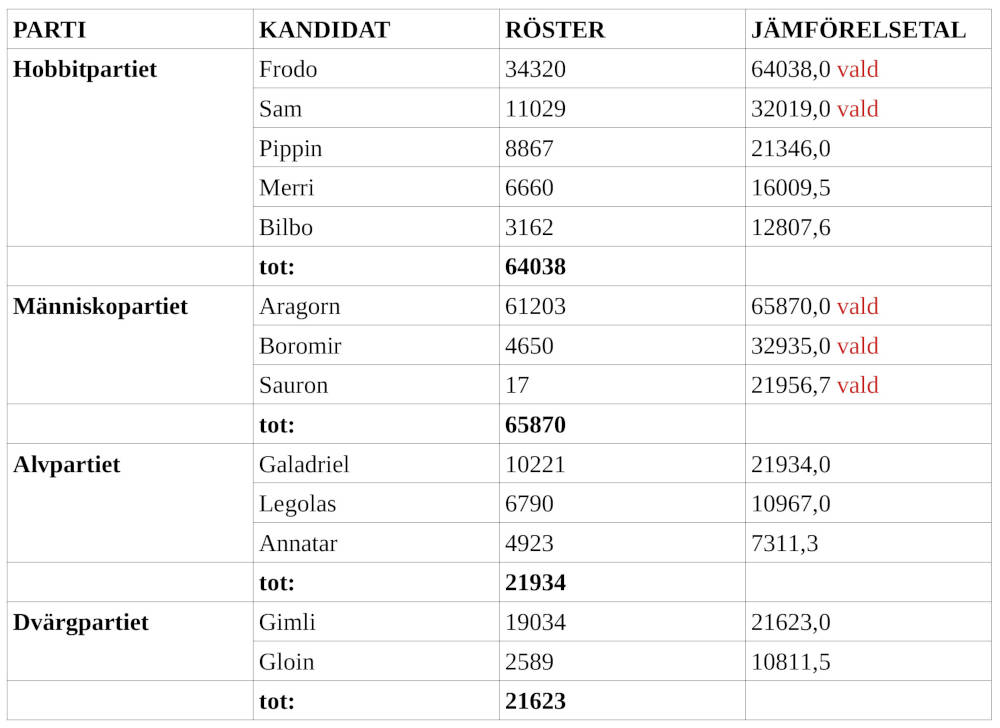 Tabell: Tabell med de rätta talen
|