Beskrivningar av goda svar: SV – Matematik, lång lärokurs
19.3.2025
Slutgiltiga beskrivningar av goda svar 13.5.2025
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i hakparentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- Om inget annat anges, godkänns även en gällande siffra fler eller färre än i anvisningarna.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
-
Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Ordet STOP betyder att raden beskriver villkor som måste uppfyllas för att kunna få poäng för den fortsatta lösningen.
-
Terminologi
- "Svar räcker" betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- "Startpoäng" betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- "maxN" betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- "Svaret endast som närmevärde" betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (till exempel noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (till exempel e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (till exempel e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (till exempel x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (till exempel parenteser som fattas men korrekt beräknat; =-tecknet använt "i kedja", m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
15.5.2025 kl. 10.30 poäng som saknades i deluppgift 13.2 tillagd.
Del A
1. Basuppgifter 12 p.
I den här uppgiften ska du endast ange svaret utan motiveringar. Du kan endast skriva in ett heltal i svarsfältet.
1.1 Lös ekvationen 5 x -17 =43. 2 p.
- 12 (2 p.)
1.2 Lös potensekvationen 2 x^3 -128 =0. 2 p.
- 4 (2 p.)
1.3 Lös ekvationen sin x /2 =1/2 då 0^@ < x < 90^@. 2 p.
- 60 (2 p.)
1.4 Bestäm f'(2), då f(x) =x^4 +100. 2 p.
- 32 (2 p.)
1.5 Bestäm värdet på integralen A =int_1^4 3 x^2 dx . 2 p.
- 63 (2 p.)
1.6 Bestäm den trettionde termen a_30 i den aritmetiska talföljden (a_1, a_2, a_3, ...) =(1, 8, 15, ...). 2 p.
- 204 (2 p.)
- 211 (1 p.)
- 197 (1 p.)
2. Förenklingar 12 p.
- Förenkla uttrycket (y^2 -4) (y +1) /(y -2) , då y !=2. (6 p.)
- Förenkla uttrycket sqrt((z -1)^2 +2 (z -1) +1). (6 p.)
Deluppgift 2.1
Faktoriserat (y^2-4) till (y-2)(y+2) (2 p.)
Förkortat (y-2) korrekt (exempelvis fått (y+2)(y+1)) (2 p.)
Skrivit uttrycket i formen y^2 +y+2y +2 [1 p.]
Skrivit uttrycket i formen y^2+3y+2 (1 p.)
Särskilda anvisningar för deluppgiften
Startpoäng: öppnat upp parenteserna i täljaren även med kopieringsfel. (1 p.)
Markerat som ekvation: poäng för de olika korrekta delstegen i förenklingen och därefter -1 p.
Förenklat y^2-4 =(y-2)^2 eller liknande produkt av två 1.a-gradspolynom. (0+2+1+1) (max 4 p.)
Korrekt förenkling men fortsatt till ekvationen y^2+3y+2=0. (max 5 p.)
Kopieringsfel: i sista faktorn (y+1). (2+2+0+0) (max 4 p.)
Kopieringsfel: första faktorn (y^2-2) eller motsvarande. (1+0+0+0) (max 1 p.)
Deluppgift 2.2
Skrivit radikanden i formen z^2-2z+1+2z-2+1 eller i formen ((z-1)+1)^2. (2 p.)
Skrivit uttrycket i formen \sqrt{z^2}. (1 p.)
Fått svaret: |z| (3 p.) ELLER fått |z| men fortsatt felaktigt (2 p.) ELLER svaret z eller \pm z (1 p.) (3 p.)
Särskilda anvisningar för deluppgiften
Startpoäng: öppnat upp åtminstone en av parenteserna i den korrekta radikanden eller i en felaktigt kopierad radikand. (1 p.)
Fel definitionsmängd för variabeln z (exempelvis z \ge 0). (-1 p.)
Markerat som ekvation: poäng för de olika korrekta delstegen i förenklingen och därefter -1 p.
Kopieringsfel där radikanden inte blir z^2. (1+0+0) (max 1 p.)
Särskilda anvisningar för uppgiften
Namnet på variabeln byts systematiskt utan förklaring: -1 p./deluppgift. Exempelvis \sqrt{z^2} och därefter |x| hör till denna kategori.
Likhetstecknet saknas mellan de olika mellanstegen men mellanstegen är exempelvis skrivna under varandra eller tydliga på annat sätt. (-0 p.)
3. Rätvinkliga trianglar 12 p.
I en rätvinklig triangel ABC är sidornas längder |AB| =3, |AC| =4 och |BC| =5. Från den räta vinkeln A ritas en höjd vinkelrätt mot hypotenusan till punkten D. Från punkten D ritas vidare en sträcka som är vinkelrät mot kateten AC till punkten E. Slutresultatet har skissats i figur .
Bestäm kateternas längder i triangeln ADE .
Trigonometri
En korrekt trigonometrisk ekvation för en vinkel, till exempel \sin\alpha=\frac35 eller \alpha= \operatorname{arccos}(\frac45). (2 p.)
Utifrån ekvationen \sin (\measuredangle DBA)=\frac{|AD|}{3} eller \sin (\measuredangle ACD)=\frac{|AD|}{4} får vi |AD|=\frac{12}{5}\ (=2{,}4). (2 p.)
poäng oberoende av de ovanstående raderna Trianglarna ADE och ABC är likformiga och motivering: vinklarna är lika stora (vv). (1+1 p.)
Då gäller \sin (\measuredangle ACB)=\sin (\measuredangle EDA) och \cos (\measuredangle ACB)=\cos (\measuredangle EDA), varifrån vi får \frac{|AE|}{|AD|}=\frac{|AB|}{|BC|} och \frac{|ED|}{|AD|}=\frac{|AC|}{|BC|}. (1+1 p.)
Beräknat de exakta värdena |ED|=\frac{48}{25} \ (=1{,}92) och |EA|=\frac{36}{25}\ (=1{,}44). (2+2 p.)
Särskilda anvisningar för denna lösning
I lösningar med närmevärden kan mellanstegen avvika ganska mycket från ovanstående.
ELLER Proportionalitet
Triangelns area kan beräknas med hjälp av kateterna och med hjälp av hypotenusan |BC| och den höjd |AD| som är vinkelrät mot hypotenusan, (2 p.)
det vill säga \frac{1}{2}|AD|\cdot 5=\frac{1}{2}\cdot 3\cdot 4, så med andra ord är |AD|=\frac{12}{5}. (2 p.)
ELLER
Trianglarna ABC ja DAC är likformiga + \frac{|AB|}{|BC|}=\frac{|AD|}{|AC|} eller motsvarande proportionalitet. (1+1 p.)
Utifrån proportionalitetsekvationen får vi |AD|=\frac{12}{5}\ (=2{,}4). (2 p.)
ELLER
Vi bildar ett ekvationssystem med hjälp av Pythagoras sats exempelvis med talen
x=|AD| och y=|DB|: x^2+y^2=3^2 och x^2+(5-y)^2=4^2. (2 p.)
Vi får lösningen |AD|=\frac{12}{5}\ (= 2{,}4). (2 p.)
poäng oberoende av de ovanstående raderna Trianglarna EAD och ABC är likformiga och motivering: vinklarna är lika stora (vv). (1+1 p.)
Vi får proportionalitetsekvationen \frac{|AE|}{|AD|}=\frac{|AB|}{|BC|} eller \frac{|ED|}{|AD|}=\frac{|AC|}{|BC|}, (2 p.)
varifrån vi får de exakta värdena för kateterna
|AE|=\frac{3}{5}\cdot \frac{12}{5}=\frac{36}{25}\ (=1{,}44) och |ED|=\frac{4}{5}\cdot \frac{12}{5}=\frac{48}{25} \ (=1{,}92). (2+2 p.)
Särskilda anvisningar för denna lösning
I påståendet om likformighet krävs inte att motsvarande vinklar är i samma ordning, exempelvis duger "trianglarna ADE och ABC är likformiga" också.
ELLER Analytisk geometri
Vi placerar triangelns hörn i ett koordinatsystem, exempelvis i punkterna
A=(4,0), B=(4,3) och C=(0,0), som vi använder nedan. (1 p.)
Ekvationen för den linje som går genom punkterna B och C är y=\frac34 x. (1 p.)
Ekvationen för den linje som går genom punkterna A och D är y=-\frac43 x+\frac{16}{3}
(termerna 1+1, uträkningarna eller motiveringarna 1+1). (4 p.)
Lösning av ekvationssystemet ger D =\big(\frac{64}{25},\frac{48}{25}\big)
(bra början 2 p., lösning 2 p.), (2+2 p.)
det vill säga de exakta värdena för kateterna är
|ED|=\frac{48}{25} \ (=1{,}92) och |AE|=4-\frac{64}{25}=\frac{36}{25}\ (=1{,}44). (1+1 p.)
Särskilda anvisningar för uppgiften
Närmevärden i svaret eller i mellanstegen: från svarsraden -1 och från den raden där man först frångår exakta värden -1. Utöver det kan allmänt avdrag tillämpas.
Exempelvis {cos(arcsin(4/5))=0,6} utan motivering (antas att räknare har använts). (-2 p.)
Även hypotenusan finns i svaret utan att den nämns som hypotenusa. (-1 p.)
Oförkortat bråk (utan exakt värde i decimalform). (-1 p.)
Exakt värde och avrundat decimaltal som svar. (-0 p.)
Beteckning för en sträckas längd utan absolutbelopp godkänns, exempelvis AD. (-0 p.)
4. ECB:s räntebeslut 12 p.
Europeiska centralbanken (ECB) ska besluta om en styrränta, som för närvarande ligger på 4,25 %. En grupp ekonomer bedömer att sannolikheten för en höjning av styrräntan med 0,25 procentenheter är 50 % och att sannolikheten för att styrräntan hålls oförändrad är 50 %. När ny information om inflationen läcker ut i offentligheten korrigerar ekonomerna sin prognos för en höjning med 0,25 procentenheter till en sannolikhet på 65 %, vilket ger en sannolikhet på 35 % för att räntan ska hållas oförändrad.
Hur mycket stiger väntevärdet för styrräntan uttryckt i procentenheter som följd av den nya informationen?
Då styrräntan höjs med 0,25 procentenheter blir styrräntan 4,5 %. [1 p.]
Väntevärdet för styrräntan i procent utifrån den gamla informationen är 0{,}5\cdot4{,}25+0{,}5\cdot4{,}5 =4{,}375 (båda produkterna tillsammans 1 p., summan 1 p., svaret 1 p.; poäng för summan endast om den är av formen snl\cdotränta+snl\cdotränta). (3 p.)
Väntevärdet för styrräntan i procent utifrån den nya informationen är 0{,}35\cdot4{,}25+0{,}65\cdot 4{,}5 =4{,}4125 (produkterna 1+1 p., summan 1 p., svaret 1 p., poäng för summan endast om den är av formen snl\cdotränta+snl\cdotränta). (4 p.)
Väntevärdet för styrräntan ökar med 4{,}4125-4{,}375 = ganska exakt {0{,}0375} eller ganska exakt {0{,}038} eller ganska exakt {0{,}04} procentenheter (endast dessa noggrannheter; differensen av väntevärdena beräknad utifrån korrekta principer 1 p., svaret 2 p., svaret i procentenheter 1 p.). (4 p.)
Särskilda anvisningar för denna lösning
Beräknat utan tilläggsmotiveringar 4{,}25 + 0{,}5\cdot 0{,}25 = 4{,}375 och 4{,}25 + 0{,}65\cdot 0{,}25 = 4{,}4125 (1+(0+0+1)+(1+1+1)+4). (max 9 p.)
Beräknat höjningen av styrräntan fel i början 4\mathrm{,}25\cdot 1\mathrm{,}0025: (0+3+4+2) (max 9 p.)
ELLER
Väntevärdet för höjningen av styrräntan i procentenheter utifrån den gamla informationen är 0{,}5\cdot 0+0{,}5\cdot0{,}25 =0{,}125 (produkterna 1+1 p, summan 1 p., svaret 1 p.; poäng för summan endast om den är av formen snl\cdotränta+snl\cdotränta). (4 p.)
Väntevärdet för höjningen av styrräntan i procentenheter utifrån den gamla informationen är 0{,}35\cdot 0+0{,}65\cdot 0{,}25 =0{,}1625 (produkterna 1+1 p., summan 1 p., svaret 1 p., poäng för summan endast om den är av formen tn\cdotkorko+tn\cdotkorko). (4 p.)
Väntevärdet för styrräntan ökar med 0{,}1625-0{,}125= ganska exakt {0{,}0375} eller ganska exakt {0{,}038} eller ganska exakt {0{,}04} procentenheter (endast dessa noggrannheter; differensen av väntevärdenas höjning beräknad utifrån korrekta principer 1 p., svaret 2 p., svaret i procentenheter 1 p.). (4 p.)
Särskilda anvisningar för denna lösning
Enbart uträkningar utan meningsfulla motiveringar 0{,}5\cdot 0{,}25 och 0{,}65\cdot 0{,}25 ((1+0+1)+(1+0+1)+4). (max 8 p.)
5. Största värde 12 p.
Bestäm det största värdet för funktionen f(x) =x^2025 e^-x då x >= 0.
Deriverat x^{2025} korrekt D(x^{2025})=2025x^{2024}. (1 p.)
Deriverat e^{-x} korrekt D(e^{-x})=-e^{-x} (eller vid användning av derivatan av en kvot e^x deriverat korrekt). (1 p.)
Använt regeln för derivering av en produkt/kvot korrekt på båda termerna.
f'(x)=2025x^{2024}e^{-x}-x^{2025}e^{-x} (1+1 p.)
Inga poäng från raden om f'(0)\ne0 eller om f' inte är en summa/differens av två termer. Den egna derivatan skriven i produktform för att lösa ut nollställena (e^{-x}x^{2024}(2025-x)) ELLER fått ekvationen 2025x^{2024}=x^{2025} och fortsatt genom att konstatera att x kan vara noll. (1 p.)
Således är derivatans enda nollställen x=0 och x=2025. (1+1 p.)
Inga poäng för fortsättningen om man inte fått minst ett derivatans nollställe där x>0.
Motiverat funktionens förlopp korrekt, exempelvis genom att utnyttja produktformen eller på följande sätt:
Beräknat derivatans värden i två punkter på vardera sidan av derivatans nollställen. Exempelvis f'(1)=2024e^{-1}>0 och f'(2026)=-e^{-2026}2026^{2024}<0. (Använt vettiga testpunkter 1 p., derivatans värden synliga i testpunkterna eller gett hållbara motiveringar 1 p.) (2 p.)
Konstaterat att f är strängt växande då (0\le) x\le 2025, och f är strängt avtagande då x\ge 2025, eller ritat ett teckenschema från vilket detta framgår. Som teckenschema räcker +|-, där | är vid 2025. (1 p.)
För fortsättningen krävs att man har fått minst två poäng på de två föregående raderna och att funktionen har ett lämpligt maximiställe.
Funktionen f antar alltså sitt största värde då x=2025. (1 p.)
Det efterfrågade värdet är f(2025)=2025^{2025}e^{-2025}. (1 p.)
Särskilda anvisningar för uppgiften
Använt ett negativt värde som testpunkt på rad 6. (-1 p.)
Som svar duger närmevärdet 1{,}16\cdot 10^{5816} utan exakt värde men inte i formen 1,16e5816 eller liknande. Alla noggrannheter godkänns.
Fått ett korrekt exakt värde som man sedan förenklat/avrundat fel. Då får man inte sista radens poäng.
Teckenschema utan motivering. (1+1+2+1+2+0+1+0+0) (max 8 p.)
Hittat nollställena genom att gissa. (1+1+2+1+0+2+1+1+1) (max 10 p.)
6. Euklides algoritm 12 p.
Bestäm med Euklides algoritm den största gemensamma faktorn för talen 5322 och 342.
Beräknat \frac{5322}{342}\approx 15{,}6 ELLER 5322=15\cdot 342 + r_1 ELLER idén 5322=q_1\cdot 342+r_1. [1 p.]
5322=15\cdot 342+192 ELLER 5322\equiv 192 \pmod{342}. (2 p.)
Vi fortsätter på samma sätt med talen 342 och 192. [1 p.]
342=1\cdot 192+150 ELLER 342\equiv 150\pmod{192}. (1 p.)
192=1\cdot 150+42 ELLER 192\equiv 42\pmod{150}. (1 p.)
150=3\cdot 42+24 ELLER 150\equiv 24\pmod{42}. (1 p.)
42=1\cdot 24+18 ELLER 42\equiv 18\pmod{24}. (1 p.)
24=1\cdot 18+6 ELLER 24\equiv 6\pmod{18} (1 p.)
18=3\cdot 6(+0) ELLER 18\equiv 0 \pmod6. (1 p.)
Gett den sista från noll avvikande resten som svar utgående från egna beräkningar. (1 p.)
Den största gemensamma faktorn är alltså exakt 6. (1 p.)
Särskilda anvisningar för uppgiften
Startpoäng: Motiverat det korrekta svaret exempelvis med SpeedCrunch-kommandot gcd / Python-kommandot math.gcd / hittat alla primfaktorer eller alla positiva faktorer. (1 p.)
Visat bara att 6 är en gemensam faktor. (0 p.)
För varje räknefel dras 1 p. av (och också från svarsraden) och ytterligare följande avdrag om algoritmen till följd av felet har
1 rad mindre (-0 p.)
2–3 rader mindre (-1 p.)
4– rader mindre (-3 p.)
Del B1
7. Teckenscheman och funktionsförlopp 12 p.
Välj i deluppgifterna 7.1–7.6 det korrekta teckenschemat eller schemat för funktionens förlopp av alternativen A–H i figur . Svaren behöver inte motiveras. Korrekt svar 2 p., fel svar 0 p., inget svar 0 p. Om du har börjat besvara uppgiften men ändå inte vill lämna in uppgiften för bedömning ska du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
7.1 f(x) =x^2 +2 x -8 2 p.
- B (2 p.)
7.2 f(x) =3 x +6 2 p.
- D (2 p.)
7.3 f(x) =2 x^2 +4 x -6 2 p.
- A (2 p.)
7.4 f(x) =4 -x -x^3 2 p.
- F (2 p.)
7.5 f(x) =3 x^2 +9 x +6 2 p.
- H (2 p.)
7.6 f(x) =2 x -5 2 p.
- E (2 p.)
8. Längder på sträckor 12 p.
I ett plan finns punkterna A=(-6,-1), B=(-1,11) och C=(8,-1). Vi väljer punkten X på sträckan AB, punkten Y på sträckan BC och punkten Z på sträckan AC så att |AX|=|AZ|=a, |BX|=|BY|=b och |CZ|=|CY|=c.
Bilda ett ekvationssystem för talen a, b och c och lös det.
|AC|=14 (ingen motivering behövs) ELLER |AC|=\sqrt{(8-(-6))^2+(-1-(-1))^2} (1 p.)
|AB|=\sqrt{(-6-(-1))^2+(-1-11)^2}\ (=13)
och |BC|=\sqrt{(-1-8)^2+(11-(-1))^2}\ (=15).
ELLER
|AB|=13 och |BC|=15 och (exempelvis GeoGebras) kommandon synliga. (2 p.)
Vi bildar korrekta ekvationer utifrån de egna sidlängderna, exempelvis: a+b=13, a+c=14 och b+c=15. (2 p./ekvation) (6 p.)
Försökt lösa det egna ekvationssystemet och fått en positiv lösning. (1 p.)
Exempelvis med Solve-kommandot eller genom att eliminera får vi ganska exakt a=6, b=7, c=8. (Antingen 0 eller 2 p.)
Särskilda anvisningar för denna lösning
Sträckorna utan motivering. (1+0+6+1+2) (max 10 p.)
Ekvationerna a+b=13, a+c=14, b+c = 15 dyker upp från ingenstans (0+0+6+1+2) (max 9 p.)
Felaktiga punkter A, B eller C: från två första raderna max 2 p. för två korrekt uträknade sträckor utifrån de egna punkterna, inga poäng från sista raden. (max 9 p.)
Löst utan ekvationssystem, exempelvis en ungefärlig (GeoGebra-)bild från vilken man dragit slutsatsen a=6, b=7, c=8. (1+2+0+0+0) (max 3 p.)
ELLER (med hjälp av linjer eller vektorer utan att först bestämma längden av sträckorna, innehåller extra variabler)
Framställt koordinaterna för punkten X med hjälp av en parameter.
Exempelvis ekvationen för linjen mellan punkterna A och B (-12x+5y=67 och X=(s,\frac{12}{5}s+\frac{67}{5})) eller med hjälp av vektorer (-6\overline{i}-\overline{j}+s (5\overline{i} + 12 \overline{j})). (1 p.)
Framställt koordinaterna för punkten Y med hjälp av en parameter.
Exempelvis ekvationen för linjen mellan punkterna B och C (4x+3y=29 och Y=(t,\frac{-4}{3}t+\frac{29}{3})) eller med hjälp av vektorer (-\overline{i}+11\overline{j}+t (9\overline{i} - 12 \overline{j})). (1 p.)
Framställt koordinaterna för punkten Z med hjälp av en parameter.
Exempelvis (v,-1) eller -6\overline{i}-\overline{j}+v\, \overline{i}. (1 p.)
Bildat ekvationer för avstånden med hjälp av koordinaterna
a=\sqrt{(s-(-6))^2+(\frac{12}{5}s+\frac{67}{5}-(-1))^2}=\sqrt{(v-(-6))^2-(-1-(-1))^2}
b=\sqrt{(s-(-1))^2+(\frac{12}{5}s+\frac{67}{5}-11)^2}=\sqrt{(t-(-1))^2+(\frac{-4}{3}t+\frac{29}{3}-11)^2}
c=\sqrt{(v-8)^2+(-1-(-1))^2}=\sqrt{(t-8)^2+(\frac{-4}{3}t+\frac{29}{3}-(-1))^2}
(1 p./korrekt ekvation) eller motsvarande. (6 p.)
Försökt lösa det egna ekvationssystemet och fått en positiv lösning för talen a, b, c. (1 p.)
Exempelvis med Solve-kommandot eller genom att eliminera får vi ganska exakt a=6, b=7, c=8. (Antingen 0 eller 2 p.)
Särskilda anvisningar för uppgiften
Ekvationssystemet innehåller inte explicit variablerna a, b och c (en poäng per variabel) ELLER lösryckta ekvationer, som inte sammanställs, istället för ett ekvationssystem. Klammerbeteckning krävs inte. Från raden med 6 p. (-3 p.)
9. Afrikas stjärna 12 p.
Det finns 30 spelbrickor i spelet Afrikas stjärna: 12 blanka, 5 hästskor, 3 rövare, 4 gula topaser, 3 gröna smaragder, 2 röda rubiner och 1 Afrikas stjärna-diamant. I början av spelet blandas brickorna och placeras upp och nedvända på spelplanen, varvid alla brickor ser likadana ut. Då spelaren vänder en bricka tas den bort från spelet. Spelpjäserna flyttas på spelplanen genom att man kastar en tärning; spelpjäsens placering avgör vilken bricka som kan vändas.
9.1 Välj korrekt alternativ. 4 p.
9.1.1 Den första spelbrickan som du vänder är blank och den andra är en rubin. 1 p.
- Händelserna är beroende av varandra. (1 p.)
9.1.2 Den spelbricka som du vänder visar sig vara en topas, och du får ögontalet 4 på följande kast. 1 p.
- Händelserna är oberoende av varandra. (1 p.)
9.1.3 Du får ögontalet 6 på tärningen på din kasttur och motspelaren får ögontalet 4 på sin kasttur. 1 p.
- Händelserna är oberoende av varandra. (1 p.)
9.1.4 Du får en rövare på en spelbricka och motspelaren får en smaragd på sin spelbricka. 1 p.
- Händelserna är beroende av varandra. (1 p.)
9.2 Besvara frågorna i deluppgifterna 9.2.1–9.2.2 på normalt sätt med motiveringar. 8 p.
- Med vilken sannolikhet får du på två kast minst summan 10 på tärningarnas ögontal? (4 p.)
- Hittills har det i spelet vänts sju blanka, en topas, en rubin och en rövare. Med vilken sannolikhet finns antingen Afrikas stjärna eller en hästsko på följande spelbricka som vänds? (4 p.)
Deluppgift 9.2.1
Med två tärningar finns det 36 kombinationer. För det här räcker det att talet 36 syns i ett vettigt sammanhang, exempelvis att sannolikheten för ett givet ögontal är \frac{1}{36} eller att svaret är \frac{6}{36}. (1 p.)
Av dessa duger 4+6,\ 5+5,\ 6+4, \ 5+6,\ 6+5,\ 6+6. (Om antalet saknade/felaktiga utfall avviker med högst två från dessa gynnsamma utfall: 1 p.) (2 p.)
Den efterfrågade sannolikheten är ganska exakt \frac{6}{36}\,(=\frac{1}{6}\approx 0{,}17). (1 p.)
Särskilda anvisningar för deluppgiften
Endast svaret \frac16 eller 0,17. (0 p.)
Endast svaret \frac6{36} (1+0+0). (1 p.)
Ordningen inte beaktad och resultatet \frac{4}{21} (0+1+0). (max 1 p.)
Konstaterat att antalet gynnsamma utfall är 6 utan motivering (1+0+1). (max 2 p.)
De gynnsamma utfallen behöver inte räknas upp specifikt om man har gjort en tydlig tabell där summorna syns.
Deluppgift 9.2.2
Fått antalet kvarvarande spelbrickor 20 med motivering. Har exempelvis beräknat 20=30-10 eller gjort en lista med kvarvarande spelbrickor. (1 p.)
Gynnsamma brickor är 5 hästskor och 1 Afrikas stjärna. (1 p.)
Motsvarande sannolikheter är \frac{5}{20} och \frac{1}{20}. [1 p.]
Den efterfrågade sannolikheten är alltså \frac{6}{20}\,(=\frac{3}{10}=0{,}3). (1 p.)
Särskilda anvisningar för deluppgiften
Börjat direkt från sannolikheterna \frac{5}{20} och \frac{1}{20} utan motiveringar (0+0+1+1). (2 p.)
Endast svaret \frac6{20}, \frac3{10} eller 0,3. (0 p.)
10. Exponentialfördelningen 12 p.
Exponentialfördelningen kan exempelvis användas för att göra modeller för partikelstrålning eller kundströmmar. Fördelningens täthetsfunktion (med konstanten ~l > 0) är
f_\lambda (x) = \begin{cases} \lambda e^{-\lambda x}, & \text{då } x\ge 0,\\ 0 &\text{annars.} \end{cases}
Den stokastiska variabeln X följer den här fördelningen. Bestäm sannolikheten P(X\geq 7), som beror av konstanten \lambda.
Ett försök till att integrera en vettig funktion (som anknyter till uppgiftbeskrivningen) som innehåller \lambda:
P(X< 7)=\int_0^7 \lambda e^{-\lambda x}\, dx ELLER P(X\geq 7)= \int_7^{\infty} \lambda e^{-\lambda x}\, dx
Vänstra ledet är P(X<7) eller P(X\ge 7) 1 p., gränserna är korrekta 2 p., gränserna motsvarar vänstra ledet 1 p., funktionen är korrekt 1 p. (5 p.)
Vi utnyttjar kedjeregeln för en sammansatt funktion:
\int_0^7 \lambda e^{-\lambda x}\, dx=- \int_0^7 (-\lambda) e^{-\lambda x} \, dx= 1- e^{-7 \lambda}, det vill säga P(X\geq 7)\,(=1-(1- e^{-7 \lambda}))=e^{-7\lambda}
eller
P(X\geq 7)=\int_7^\infty \lambda e^{-\lambda x}\, dx=- \int_7^\infty (-\lambda) e^{-\lambda x} \, dx =e^{-7 \lambda}
(försökt använda kedjeregeln på ett vettigt sätt 1 p. / integreringen (koefficienten -1: 1 p. och e^{-\lambda x} 1 p.) / insättningen 1 p. / förenklingen 1 p.)
ELLER
Vi gör en variabelsubstitution y=\lambda x och får dy=\lambda \, dx med integrationsgränserna 0 och 7\lambda.
Fått \int_0^7 \lambda e^{-\lambda x}\, dx=\int_0^{7\lambda} e^{-y}\, dy=1-e^{-7\lambda} det vill säga P(X\geq 7) =e^{-7\lambda}.
eller
Fått P(X\geq 7)= \int_7^{\infty} \lambda e^{-\lambda x}\, dx=\int_{7\lambda}^{\infty} e^{-y}\, dy =e^{-7\lambda}.
(variabelbyte 1 p./ gränserna 1+1 p./ uträkningen (utan gränsvärde) 2 p.)
ELLER
Använt räknaren för att integrera en vettig funktion (som anknyter till uppgiftbeskrivningen) som innehåller \lambda 1 p. Integreringen har löst uppgiften 2 p. Slutsats: Lösningen är väldokumenterad och alla kommandon och resultat som behövs är synliga. 1 p. Lösningen är i förenklad form. 1 p. (5 p.)
oberoende Motivering: P(X\geq 7)=1-P(X<7) ELLER korrekt behandling av gränsvärdet i det generaliserade fallet (exempelvis \int_{7}^{\infty} \lambda e^{-\lambda x }\, dx=\lim_{t\to \infty} \int_{7}^{t} \lambda e^{-\lambda x}\, dx), även i räknarlösningar. (2 p.)
Särskilda anvisningar för uppgiften
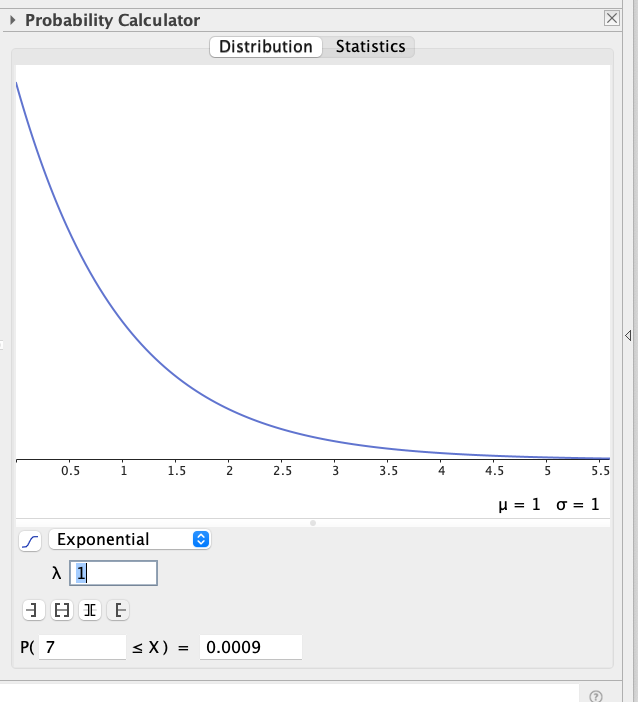
Startpoäng: Beräknat fördelningsfunktionens värde för någon konstant \lambda, exempelvis \lambda=1, ELLER en skärmdump i stil med den nedan från Geogebra.
Inget gränsvärde i integalerna till exempel insättning av värdena 7 och \infty rakt i integralfunktionen. (max 10 p.)
Har använt gränsvärde och har satt in oändligheten vid beräkning av gränsvärdet. (max 11 p.)
I en av tabellsamlingarna i provsystemet saknades minustecknet från exponentialfördelningen. Om uppgiften är löst utgående från den felaktiga formeln i tabellsamlingen och kopplingen till tabellsamlingen är tydligt dokumenterad så gäller max 12.
Del B2
11. Korrekt eller felaktig? 12 p.
-
Olivia deriverar funktionen f(x)=\frac{x^3-2x+1}{10} på följande sätt:
f'x =(10 D(x^3 -2 x +1) -(D10) (x^3 -2 x +1) / 10^2 =10 D(x^3 -2 x +1) /10^2 =(3 x^2 -2) /10.
Är slutledningen korrekt eller felaktig? Korrigera möjliga fel. Härled även slutresultatet på ett enklare sätt. (4 p.)
-
Leo utreder på följande sätt hur många nollor talet 2000! -10^300 slutar på:
I fakulteten multipliceras på varandra efterföljande tal från och med ett, alltså får man alltid en nolla sist i talet då man kommer fram till tio. Antalet tal delbara med tio i produkten är \frac{2000}{10}=200. Dessutom kommer det en nolla sist i talet om produkten innehåller en faktor som är delbar med två och en faktor som är delbar med fem. Talen delbara med två ligger så tätt att det räcker med att granska talen som är delbara med fem. De är \frac{2000}{5}=400 till antalet. I det första talet finns det alltså totalt 200+400=600 nollor. I det andra talet finns det 300 nollor. I differensen finns det därmed 600-300=300 nollor.
Efter detta kontrollerade Leo med räknaren, och räknaren gav som resultat ett 5736-siffrigt tal, som avslutades med 300 nollor. Utgående från detta konstaterade han att han hade gjort en korrekt slutledning.
Är slutledningen korrekt eller felaktig? Korrigera möjliga fel. (8 p.)
Deluppgift 11.1
Lösningen innehåller formeln D\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2} eller deriveringsregeln för en kvot är nämnd. (1 p.)
I lösningen har man förklarat hur Olivias slutledning relaterar till formeln, exempelvis genom att konstatera att f(x)=x^3-2x+1 och g(x)=10, varvid f'(x)=3x^2-2 och g'(x)=0 och har konstaterat att lösningen är korrekt. (Konstaterandet kan vara i början av lösningen men poäng ges endast om konstaterandet också är motiverat.) (1 p.)
oberoende Lättare sätt: f'(x)=\frac{1}{10}D(x^3-2x+1)=\frac{1}{10}(3x^2-2) eller annan användning av formeln D(kf(x))=k f'(x). (2 p.)
Särskilda anvisningar för deluppgiften
Endast svar eller motiverat att lösningen är korrekt genom att jämföra med slutresultatet \frac{3x^2-2}{10} (ex. från räknaren eller från det lättare sättet). (+0 p.)
Nämnt ordningen som fel, exempelvis D(x^3-2x+1)\cdot 10. (\pm0 p.)
Använt deriveringsregeln för en produkt som lättare sätt. (+0 p.)
Deluppgift 11.2
oberoende I lösningen har antalet nollor i talet x-y beräknats felaktigt genom att subtrahera antalet nollor i talet y från antalet nollor i talet x. (1 p.)
Dessutom har det gjorts fel i beräkningen av antalet nollor i det första talet:
oberoende En del nollor har beräknats flera gånger eftersom alla tal som är delbara med talet 10 är också delbara med talet 5. (1 p.)
oberoende En del nollor har glömts bort eftersom vissa tal är delbara med högre potenser av talet 5, exempelvis är talet 25 två gånger delbart med talet 5 ELLER "en del nollor har glömts bort i talen 100, 200, \ldots" (1 p.)
Slutledningen har konstaterats vara felaktig på grund av upptäckten av ett eller flera fel eller genom att beräkna det korrekta antalet nollor. Konstaterandet kan vara i början av lösningen men poäng ges endast om det är motiverat. (1 p.)
Korrigerad lösning:
Antalet nollor i talet x-y är lika med antalet nollor i det tal x eller y som innehåller färre nollor (om antalet nollor är olika). (1 p.)
Dragit en välmotiverad slutsats om att antalet nollor i talet 2000! är över 300. (2 p.)
Talet 10^{300} har 300 nollor (dvs färre) och därför är det också antalet nollor i differensen. (1 p.)
Särskilda anvisningar för deluppgiften
Hittat ett "fel" som inte är ett fel, totalt. (-1 p.)
Om det i beräkningen (eller uppskattningen) av antalet nollor i talet 2000! finns fel men resultatet är över 300: max 1+1+1 från de tre sista raderna. Till denna kategori hör också fallet "talet har exakt 400 nollor".
Antalet nollor i talet 2000! är \frac{2000}5+\frac{2000}{25}+\frac{2000}{125}+\lfloor\frac{2000}{625}\rfloor=499, men denna information är inte nödvändig efter att det första steget i lösningen är korrigerat.
Korrektheten i slutledningen kan inte motiveras med att det numeriska svaret är korrekt. (+0 p.)
Det korrekta antalet nollor i talet 2000! (dvs 499) med motiveringar och konstaterandet att det finns ett fel ger också poängen för raderna 2 och 3.
12. En integral som ska uppskattas 12 p.
Anta att n >= 0 är ett heltal. Bevisa olikheten
int_0^1 sin(~p x) (x (1 +x) (1 -x))^n dx <= 2 /~p *(2 /(3 sqrt(3))^n.
Ledtråd: Om f(x)\leq g(x) i intervallet [0,1], så är \int_0^1f(x)\,dx \leq\int_0^1 g(x)\,dx.
Undersökt på något sätt funktionen g(x)=x(1+x)(1-x) eller
h(x)=(x(1+x)(1-x))^n för något n> 0. Exempelvis förenklat till g(x)=x-x^3 eller ritat dess graf. [1 p.]
g'(x)=1-3x^2, vars nollställen är x=\pm\frac{1}{\sqrt{3}} (eller endast den positiva med motivering). (1 p.)
Motiverat att x=\frac{1}{\sqrt{3}} är ett maximiställe. (1 p.)
oberoende Det största värdet i intervallet [0,1] är g\big(\frac{1}{\sqrt{3}}\big)=\frac{2}{3\sqrt{3}} ELLER motiverat med grafer eller med solve-kommandot att g\left(x\right)\le\frac{2}{3\sqrt{3}} i intervallet [0, 1]. (2 p.)
(g\left(x\right)\ge0 i intervallet [0,1]), dvs g(x)^n\le\big(\frac{2}{3\sqrt{3}}\big)^n. (1 p.)
oberoende Konstaterat att \sin\left(\pi x\right)\ge0 i intervallet [0, 1]. (1 p.)
\int_0^1\sin\left(\pi x\right)\left(x(1+x)\left(1-x\right)\right)^n\, dx\le\int_0^1\sin\left(\pi x\right)\cdot\big(\frac{2}{3\sqrt{3}}\big)^n\, dx (1 p.)
=\big(\frac{2}{3\sqrt{3}}\big)^n\int_0^1\sin\left(\pi x\right)\, dx. (1 p.)
oberoende \int_0^1\sin\left(\pi x\right)\ dx\bigg(=\frac{1}{\pi}\Big/_{\!\!\!\!0}^1-\cos(\pi x)\bigg)=\frac{2}{\pi} (1+1 p.)
Slutsatsen \int_0^1\sin\left(\pi x\right)\left(x\left(1+x\right)\left(1-x\right)\right)^n\, dx\le\frac{2}{\pi}\big(\frac{2}{3\sqrt{3}}\big)^n. (1 p.)
Särskilda anvisningar för uppgiften
Startpoäng: Motiverat exempelvis med närmevärden eller med olikhetens sanningsvärde att olikheten är sann för något n\ge 0. Startpoängen fås inte om olikhetens högra led innehåller integralen av den övre gränsen i intervallet [0, 1]. (1 p.)
Raderna 2 och 3 kan ersättas med fmax-kommandot.
Raderna 2–4 kan ersättas med Extrempunkt-kommandot med exakta värden (Geogebra).
Om man gjort uppskattningen \sin\left(\pi x\right)\le1, varvid man undersökt påståendet
\int_0^1\left(x\left(1+x\right)\left(1-x\right)\right)^n\ dx\le\frac{2}{\pi}\left(\frac{2}{3\sqrt{3}}\right)^n:\ 1+1+1+2+1+1+0 (max 7 p.)
13. Kryssprodukt av vektorer 12 p.
Kryssprodukten av vektorerna \overline{a}=a_x\overline{i}+a_y\overline{j}+a_z\overline{k}och\overline{b}=b_x\overline{i}+b_y\overline{j}+b_z\overline{k} definieras med uttrycket
vec a * vec b =(a_y b_z -a_z b_y) vec i +(a_z b_x -a_x b_z) vec j +(a_x b_y -a_y b_x) vec k.
Använd uttrycket för att bevisa följande kända egenskaper hos kryssproduktvektorn:
- Den är vinkelrät mot vektorn vec a. (3 p.)
- Dess längd är lika stor som arean av den parallellogram som vektorerna vec a och vec b spänner upp. (9 p.)
Deluppgift 13.1
Vi beräknar den skalära produkten av kryssproduktvektorn och vektorn \overline{a} för hand: \overline a \cdot (\overline{a}\times \overline{b})
=a_x(a_yb_z-a_zb_y)+a_y(a_zb_x-a_xb_z)+a_z(a_xb_y-a_yb_x) (2 p.)
=a_xa_yb_z-a_xa_zb_y+a_ya_zb_x-a_ya_xb_z+a_za_xb_y-a_za_yb_x=0. (1 p.)
ELLER med programvara:
Exempelvis med SkalärProdukt- och Kryssprodukt-kommandona (i lösningen måste man konstatera att Kryssprodukt-kommandot ger samma komponenter som i uppgiftens definition, annars 0 p.) eller a_x(a_yb_z-a_zb_y)+a_y(a_zb_x-a_xb_z)+a_z(a_xb_y-a_yb_x) = 0 (3 p.)
Särskilda anvisningar för deluppgiften
Hittat ett villkor för ortogonalitet i provsystemets tabellsamlingar. (+0 p.)
Beräknat den skalära produkten med egna exempelvektorer. (+0 p.)
Betecknat produkten av reella tal med \cdot (-0 p.)
Parenteserna som anger räkneordningen saknas (a \cdot a \times b eller a \times b \cdot a), men beräkningen är korrekt utförd. (-0 p.)
Deluppgift 13.2
Cosinus för vinkeln \alpha mellan vektorerna \overline{a} och \overline{b} är \cos \alpha=\frac{\overline{a}\cdot \overline{b}}{|\overline{a}||\overline{b}|}, [1 p.]
varifrån vi får \alpha = \arccos({\frac{\overline{a}\cdot \overline{b}}{|\overline{a}||\overline{b}|}}) eller \sin\alpha = \sqrt{1-\big(\frac{\overline{a}\cdot \overline{b}}{|\overline{a}||\overline{b}|}\big)^2}. (1 p.)
Vi sätter in detta i areaformeln |\overline{a}||\overline{b}|\sin \alpha, (1 p.)
och får då exempelvis
\sqrt{(1-\cos^2(\alpha))|\overline{a}|^2|\overline{b}|^2} =\sqrt{\Big(1-\big(\frac{\overline{a}\cdot \overline{b}}{|\overline{a}||\overline{b}|}\big)^2\Big)|\overline{a}|^2|\overline{b}|^2} =\sqrt{|\overline{a}|^2|\overline{b}|^2-(\overline{a}\cdot \overline{b})^2}. [1 p.]
Fått ett uttryck som är kvadratroten ur ett polynom av komponenterna (de trigonometriska funktionerna eliminerade). (1 p.)
poäng oberoende av de ovanstående raderna Bildat uttrycket för längden av kryssproduktvektorn
\sqrt{(a_yb_z-a_zb_y)^2+(a_zb_x-a_xb_z)^2+(a_xb_y-a_yb_x)^2} genom att använda definitionen av kryssprodukten som ges i uppgiftsbeskrivningen eller genom att använda kryssprodukt med räknaren och jämfört det med definitionen i uppgiftsbeskrivningen. (2 p.)
Förenklat uttrycket (a_yb_z-a_zb_y)^2+(a_zb_x-a_xb_z)^2+(a_xb_y-a_yb_x)^2. [1 p.]
Bildat korrekta polynomuttryck för (kvadraterna på) längden och arean. Vi jämför dem (räknare ok) och konstaterar att de är lika med varandra. (1 p.)
Särskilda anvisningar för deluppgiften
Eller motsvarande beräkningar med kvadraterna (som i nedanstående formler).
På poängrad 6 ges 0 p. om man använt crossP-kommandot (eller motsvarande) utan att explicit jämföra det med definitionen i uppgiftsbeskrivningen. Om uttrycket dyker upp utan att explicit jämföra med uppgiftsbeskrivningen kan man ännu få poäng för de två sista raderna. 1+1+1+1+1+0+1+1 (max 7 p.)
Uttrycket och förenklingen av kvadraten på längden av kryssproduktvektorn är:
(a_yb_z-a_zb_y)^2+(a_zb_x-a_xb_z)^2+(a_xb_y-a_yb_x)^2=(a_yb_z)^2+(a_zb_y)^2+(a_zb_x)^2+ (a_xb_z)^2+(a_xb_y)^2+(a_yb_x)^2-2a_yb_za_zb_y-2a_zb_xa_xb_z-2a_xb_ya_yb_x
Uttrycket för kvadraten på arean är:
|\overline{a}|^2|\overline{b}|^2-(\overline{a}\cdot \overline{b})^2=(a_x^2+a_y^2+a_z^2)(b_x^2+b_y^2+b_z^2)-(a_xb_x+a_yb_y+a_zb_z)^2=a_x^2b_x^2+a_x^2b_y^2+a_x^2b_z^2+a_y^2b_x^2+ a_y^2b_y^2+a_y^2b_z^2+a_z^2b_x^2+a_z^2b_y^2+a_z^2b_z^2-(a_x^2b_x^2+a_y^2b_y^2+a_z^2b_z^2+2a_xb_xa_yb_y+2a_xb_xa_zb_z+2a_yb_ya_zb_z)= a_x^2b_y^2+a_x^2b_z^2+a_y^2b_x^2+a_y^2b_z^2+a_z^2b_x^2+a_z^2b_y^2-2a_xb_xa_yb_y-2a_xb_xa_zb_z-2a_yb_ya_zb_z