Hyvän vastauksen piirteet: FI – Matematiikka, lyhyt oppimäärä
19.3.2025
Lopulliset hyvän vastauksen piirteet 13.5.2025
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.
Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.
Miten pisteytysohjeita luetaan
- Ohjeen rakenne
- Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy pistemäärään.
- Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
- Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
- Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
- Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esimerkiksi derivaatan laskeminen osittain oikein).
- Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
- Hakasuluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
- Jos erikseen ei mainita, niin vastauksen hyväksyttävä tarkkuus on yksi merkitsevä numero enemmän tai vähemmän kuin ohjeeseen kirjattu.
- Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
- Rivien riippuvuus toisistaan
- Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esimerkiksi laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
- Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
- Merkintä yllä olevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
- Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
- Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
- Teksti STOP tarkoittaa sitä, että sillä rivillä kerrotaan, minkä ehtojen pitää toteutua, jotta jatkosta saa pisteitä.
- Terminologiaa
- "Vastaus riittää" tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
- "Alkupisteitä" tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
- "maxN" tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
- "Vastaus vain likiarvona" tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.
- Vastaus oikein, muttei pyydetyssä muodossa (esimerkiksi tarkkuus, yksikkö) -1 p.
- Vastaus sieventämättä loppuun asti sievennystehtävässä (esimerkiksi e^1, ln (e) tai 4^0) -2 p.
- Vastaus sieventämättä muussa tehtävässä (esimerkiksi e^1, ln (e) tai 4^0) -1 p.
- Ilmeiset näppäilyvirheet esityksessä (esimerkiksi x =2, y04), tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
- Vastauksessa kopiointivirhe -1 p.
- Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.
Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.
- Matemaattisesti puutteellinen merkintä (esimerkiksi puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
- Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
- Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.
A-osa
1. Lyhyitä tehtäviä 12 p.
Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.
1.1 Ratkaise yhtälö 5 x -17 =43. 2 p.
- 12 (2 p.)
1.2 Mikä on lausekkeen -7 x^2 +2 x (4 x -1) arvo kohdassa x =2? 2 p.
- 0 (2 p.)
1.3 Mikä on pisteiden (-2, -2) ja (1, 4) kautta kulkevan suoran kulmakerroin? 2 p.
- 2 (2 p.)
1.4 Mikä on edellisen osatehtävän suoran vakiotermi? 2 p.
- 2 (2 p.)
1.5 Tasakylkisen kolmion kantakulmat ovat koordinaatiston pisteissä (1, 1) ja (5, 1) . Mikä on huippukulman x-koordinaatti? 2 p.
- 3 (2 p.)
1.6 Mikä luku saadaan, kun ensimmäiset 50 positiivista paritonta kokonaislukua lasketaan yhteen, eli kuinka paljon on 1 +3 +… +97 +99? 2 p.
- 2500 (2 p.)
2. Yhtälö ja lukujono 12 p.
- Ratkaise yhtälö (x +3) (2 x -1) =4. (6 p.)
- Aritmeettisen lukujonon ensimmäinen jäsen on 2025 ja viides jäsen on 1973. Mikä on lukujonon sadas jäsen? (6 p.)
Osatehtävä 2.1
Sulkujen poisto oikein 2 x^2 -x +6 x -3 =4. (1 p.)
STOP: Ei pisteitä jatkosta, jos yhtälö ei ole toista astetta.
Termit yhdistetty oikein (2 x^2 +5 x -7 =0 TAI 2 x^2 +5 x =7). (1 p.)
Jonkinlainen aloitus yhtälön ratkaisemiseen: Sijoitettu ratkaisukaavaan omat 3 kerrointa (2, 5 ja -7) mahdollisesti väärään paikkaan tai eri merkein. Tällä rivillä kelpaa myös yhtälöstä 2 x^2 +5 x -3 =4 sijoitetut kertoimet 2, 5 ja -3. (1 p.)
Kaikki omaa normaalimuotoa vastaavat kertoimet sijoitettu oikein x =(-5 +-sqrt(5^2 -4 *2 *(-7)) /(2 *2) TAI lisätty kuvakaappaus SpeedCrunchista, josta näkyvät oikeat kertoimet. (1 p.)
Oma diskriminantti sievennetty tai käsitelty oikein. [1 p.]
Saatu juuret oikein melko täsmälleen x =1 ja x =-7/2. (Desimaalimuoto melko täsmälleen x =-3,5 käy myös.) (1 p.)
Osatehtäväkohtaiset erillisohjeet
Saatu vaillinainen toisen asteen yhtälö, a x^2 =b tai a x^2 +b x =0. (1+0+1+1+1+0) tai (0+1+1+1+1+0) (max 4 p.)
Alkupiste (1 p.): x =1 tai x =-7/2 arvattu ja tarkistettu.
Osatehtävä 2.2
(Merkitään lukujonon jäseniä a_1, a_2 jne.) Nyt a_5 -a_1 =1973 -2025 (=-52). Myös 2025 -1973 (=52) käy. (1 p.)
Kahden peräkkäisen jäsenen välinen erotus on siis -52/4 =-13. Oikea idea jakamisesta / oikea jakaja. (2 p.)
Siispä a_100 =2025 -13 *99 =738. Oikea idea vähentämisestä/ kerroin 99/ sievennetty vastaus oikein. (3 p.)
Osatehtäväkohtaiset erillisohjeet
Tyyppivirhe: luku 13 perustelematta. (0+0+3) (max 3 p.)
Tyyppivirhe: luku 13 perustelematta, mutta näytetty, että se toimii, esimerkiksi 2025 -13 -13 -13 -13 =1973. (0+2+3) (max 5 p.)
Alkupiste (1 p): Oikea idea aritmeettisesta jonosta, esimerkiksi a_100 =2025 +(100 -1) d.
3. Kokouspalkkio 12 p.
Järjestön luottamushenkilöiden kokouspalkkioita on korotettu viimeksi vuonna 2009. Vuonna 2023 järjestö päättää korottaa kokouspalkkiotaan 30 eurosta 40 euroon. Ansiotasoindeksi oli 2 717 vuonna 2009 ja 3 667 vuonna 2023. Ylittääkö luottamushenkilöiden ansiokehitys tämän jälkeen yleisen ansiokehityksen? Kuinka suuri uuden kokouspalkkion pitäisi olla, jotta korotus noudattaisi yleistä ansiokehitystä?
Indeksin muutoksen suhde (katso taulukko) TAI indeksin ja palkkion suhde vanhoilla luvuilla (2717 /30 ~~90,57 TAI 30 /2717 ~~0,0110). (lasku 3 p., vastaus 1 p.) (4 p.)
Palkkion muutoksen suhde (katso taulukko) TAI indeksin ja palkkion suhde uusilla luvuilla (3667 /40 =91,675 TAI 40 /3667 ~~0,0109). (lasku 1 p., vastaus 1 p.) (2 p.)
Kahteen oikealla logiikalla saatuun ja keskenään vertailukelpoiseen lukuun perustuen: luottamushenkilöiden ansiokehitys ei ylitä yleistä ansiokehitystä. (2 p.)
Lasketaan oikealla logiikalla yleistä ansiokehitystä noudattava kokouspalkkio (esimerkiksi 30 +0,3497 *30 tai 30 /0,7409) TAI verrantoyhtälöllä (esimerkiksi 30 /x =2717 /3667). (2 p.)
Johtopäätöksenä: Saadaan kokouspalkkioksi ~~40,49 (euroa) (tai 40,50 euroa tai 40,5 euroa, vain nämä tarkkuudet). (vastaus 1 p., pyöristys 1 p.) (2 p.)
Tehtäväkohtaiset erillisohjeet
Kerroin 0,3497/jakaja 0,7409 vähintään tämä tarkkuus tai ei pyöristyspistettä.
Vastaus 40,49 tai 40,50 tai 40,5 euroa löydetty kokeilemalla ja vastaus tarkistettu (4+2+2+1+2).
Ensimmäisen rivin nimittäjässä 3667: vaatii selityksen vertailussa tai -1 p. kolmannella rivillä.
Laskettu 40 euroa vastaava indeksiluku 2717 *40/30 ~~3623: (4+2+...) kahdelta ensimmäiseltä riviltä. Tästä pystyy tekemään johtopäätöksen (4+2+2+...).
Laskettu uuden indeksin mukainen palkkio:
– ei johtopäätöstä (4+0+0+2+2) (max 8 p.)
– tehty johtopäätös (2. riviä ei tarvitse --> sen pisteet saa, vaikka palkkio väärin) (max 12 p.)
– laskettu väärin: kerroin saattaa antaa pisteitä 1. tai 2. riviltä.
Kertoimien laskut puuttuvat mutta luvut näkyvät ja selitetty. (max 11 p.)
Pelkkä vastaus 40,49 euroa (tai vastaava) ja "40 e palkkio ei ylitä yleistä tasoa". (0 p.)
Alla olevassa taulukossa on listattu erilaisia suhteita, joita voi käyttää johtopäätöksen teossa. Myös muista sellaisista suhteista max 6 kahdelta ensimmäiseltä riviltä, joita voi käyttää johtopäätöksen tekemiseen. Suhteiden ei tarvitse olla keskenään vertailukelpoisia.
| Indeksi (4 p.) | Palkkio (2 p.) | |
|---|---|---|
| nousu | (3667 -2717) /2717 ~~34,97 % ~~35 % | (40 -30) /30 ~~33 % |
| muutoskerroin | 3667 /2717 ~~1,3497 ~~1,35 | 40 /30 ~~1,33 |
| vanha vähemmän kuin nykyinen | (3667 -2717) /3667 ~~25,91 % ~~26 % | (40 -30) /40 =25 % |
| vanhan muutoskerroin | 2717 /3667 ~~0,7409 ~0,74 | 30 /40 =0,75 |
4. Yhtälötyyppejä 12 p.
Lukiomatematiikassa on tärkeää osata erottaa potenssiyhtälöt ja eksponenttiyhtälöt toisistaan. Yksinkertaistettu potenssiyhtälö voidaan kirjoittaa muodossa x^n =t ja yksinkertaistettu eksponenttiyhtälö muodossa a^x =b. Molemmissa esimerkkiyhtälöissä tuntematon muuttuja on x.
- Anna esimerkki yksinkertaistettua muotoa olevasta potenssiyhtälöstä, jossa n >= 2 ja t !=0 ja jolla on vain yksi ratkaisu. Ratkaise myös yhtälösi. (6 p.)
- Anna esimerkki yksinkertaistettua muotoa olevasta eksponenttiyhtälöstä, jossa a > 1 ja b > 0. Ratkaise myös yhtälösi. (6 p.)
Osatehtävä 4.1
Annettu yhtälö muotoa x^n =t, jossa n >= 2 ja t !=0. (1 p.)
Oikeaa muotoa olevalla yhtälöllä x^n =t on tasan yksi ratkaisu. (1 p.)
STOP: Seuraavat pisteet voi saada vain, jos edeltä saatu kaikki 2 pistettä.
Annettu oman yhtälön oikea ratkaisu. (2 p.)
Yhtälö ratkaistu toimivalla menetelmällä. (2 p.)
Osatehtäväkohtaiset erillisohjeet
Tyyppivirhe: x^2 =4 eli x =sqrt(4) =2. (1+0+stop) (max 1 p.)
Tyyppivirhe: x^2 =4 eli x =+-sqrt(4) =+-2. (1+0+stop) (max 1 p.)
Annettu oman yhtälön oikea ratkaisu, joka testattu sijoittamalla. (1+1+2+1) (max 5 p.)
Vastauksena päättymätön desimaaliluku ja pyöristys. (max 6 p.)
Merkintävirhe, esimerkiksi otettu neliöjuuri kuutiojuuren tms. sijaan. (Ei vähennystä, jos sanallinen selitys on oikein ja juuressa ei ole indeksiä.) (-1 p.)
Osatehtävä 4.2
Annettu muotoa a^x =b oleva yhtälö omilla luvuilla. (1 p.)
Omassa muotoa a^x =b olevassa yhtälössä a > 1 ja b > 0. (1 p.)
STOP: Seuraavat pisteet voi saada vain, jos edeltä saatu kaikki 2 pistettä.
Annettu oman yhtälön oikea ratkaisu. (2 p.)
Yhtälö ratkaistu toimivalla menetelmällä TAI ratkaisu tarkistettu sijoituksella. (2 p.)
Osatehtäväkohtaiset erillisohjeet
Ilmoitettu tehtävänannon mukaiset a:n ja b:n arvot, mutta termit tai yhtälö esittämättä. (+0 p.)
Puuttuva ratkaisumenetelmä (esimerkiksi "6^x =1 eli x =0" tai "6^x =6 joten x =1"). (1+1+2+0) (max 4 p.)
Molemmat puolet esitetty saman kantaluvun avulla (esimimerkiksi "6^x =1 eli x =0, koska 6^0 =1" tai "6^x =6 =6^1, joten x =1"). (1+1+2+2) (max 6 p.)
Merkintävirhe, esimerkiksi jaettu kantaluvut puolittain pois. (-1 p.)
Annettu oman yhtälön oikea ratkaisu tuottaa pisteitä, vaikka ratkaisu olisi saatu virheellisellä laskulla/menetelmällä.
Tyyppivirhe: ylimääräiset miinusmerkit (esimerkiksi -2^x =-8, joten x =3). (0 p.)
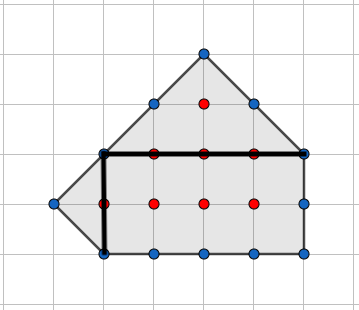
5. Pickin lause 12 p.
Pickin lause vuodelta 1899 liittyy tasogeometriaan ja monikulmioiden pinta-aloihin. Monikulmio on piirretty ruudukkoon niin, että sen kaikki kärkipisteet sijaitsevat viivojen risteyskohdissa eli hilapisteissä. Lauseen mukaan tietyntyyppisten monikulmioiden pinta-ala voidaan tällöin laskea kaavalla
(*)\qquad A = S + \frac{R}2 - 1,
jossa A on monikulmion pinta-ala ruutuina, S on monikulmion sisälle jäävien hilapisteiden lukumäärä ja R on monikulmion reunalla olevien hilapisteiden lukumäärä.
Laske kuvioiden pinta-alat ja osoita, että kaava (*) pitää paikkansa tasokuvion tapauksessa, mutta ei pidä paikkaansa tasokuvion tapauksessa.
Osatehtävä 5.1
Kuviossa A on S=8, R=12, [1 p.]
joten kaavan antama ala on melko täsmälleen 8+\frac{12}{2}-1=13. (1 p.)
Jaetaan kuvio osiin esimerkiksi seuraavasti:
Selitetty alueen jako laskettavissa oleviin osiin kuvalla tai sanallisesti. (1 p.)
Oman jaon osat laskettu oikein (suorakulmion ala 2\cdot 4=8 ja kolmioiden alat 2\cdot 1\cdot \frac{1}{2}=1 ja 4\cdot 2\cdot \frac{1}{2}=4 TAI kokonaisia ruutuja on 10 kappaletta ja puolikkaita ruutuja on 6). (Yksi ala käsittelemättä/väärin: 1 p., useampi ala: 0 p.) (2 p.)
täsmälleen Johtopäätöksenä: Ala on siis 8+1+4=13 TAI 10+\frac{1}{2}\cdot 6=13, joten kaava toimii. (1 p.)
Osatehtäväkohtaiset erillisohjeet
Todellinen pinta-ala annettu perusteluitta max 1+1+0+0+0. (max 2 p.)
Todellinen pinta-ala laskettu järkevällä lausekkeella, jota ei ole perusteltu mitenkään max 1+1+0+2+0. (max 4 p.)
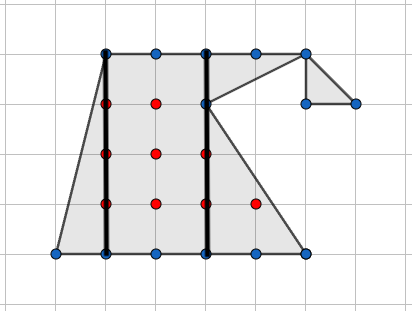
Osatehtävä 5.2
Kuviossa B on S=9, R=14, [1 p.]
joten kaavan antama ala on melko täsmälleen 9+\frac{14}{2}-1=15. (1 p.)
Jaetaan kuvio osiin esimerkiksi seuraavasti:
Selitetty alueen jako laskettavissa oleviin osiin kuvalla tai sanallisesti. (1 p.)
Oman jaon osat laskettu oikein (kolmioiden alat ovat 4\cdot 1\cdot \frac{1}{2}=2, 3\cdot 2\cdot \frac{1}{2}=3, 2\cdot 1\cdot \frac{1}{2}=1 ja 1\cdot 1\cdot \frac{1}{2}=\frac{1}{2}, suorakulmion ala on 2\cdot 4=8). (Yksi ala käsittelemättä/väärin: 1 p., useampi ala: 0 p.) (2 p.)
täsmälleen Johtopäätöksenä: Ala on siis 2+3+1+\frac{1}{2}+8=\frac{29}{2}, joten kaava ei toimi. (1 p.)
Osatehtäväkohtaiset erillisohjeet
Todellinen pinta-ala annettu perusteluitta max 1+1+0+0+0. (max 2 p.)
Todellinen pinta-ala laskettu järkevällä lausekkeella, jota ei ole perusteltu mitenkään max 1+1+0+2+0. (max 4 p.)
Tehtäväkohtaiset erillisohjeet
Viimeisen rivin piste kummassakin kohdassa vaatii, että ala laskettu perustellusti ja lauseen toimivuus/toimimattomuus todettu.
Vääriä perusteluja kaavan toimivuudelle/toimimattomuudelle. (-0 p.)
Ylimääräiset (mahdollisesti väärät tai päättömät) mittayksiköt. (-0 p.)
Tyypillinen minimalistinen ratkaisu: A: 13=8+12/2-1, joten 13 = 13 ja B: 14,5 =9+14/2-1 ja 14,5 = 15. (1+1+0+0+0/1+1+0+0+0) (4 p.)
6. Klassikko 12 p.
Määritä esimerkiksi derivaatan avulla polynomifunktion p(x) =x^3 -x^2 +x suurin ja pienin arvo, kun 1 <= x <= 2.
Lasketaan derivaatta: p'(x) =3 x^2 -2 x +1. (yksi termi ja derivaatan aste oikein 1 p., kaksi termiä oikein 1 p., kaikki termit oikein 1 p.) (3 p.)
Selvitetään omalle derivaatalle, joka on 2. asteen polynomi, onko sillä nollakohtia:
x =(2 +-sqrt((-2)^2 -4 *3 *1)) /(2 *3) =(2 +-sqrt(-8)) /(2 *3). (sijoitus likimain oikein 1 p., sijoitettu oikein omat kolme nollasta poikkeavaa termiä 1 p., diskriminantti sievennetty oikein [myös 4 -12 käy] 1 p.) (3 p.)
riippumaton Diskriminantti on negatiivinen ja todettu, että derivaatalla ei ole nollakohtia. (1 p.)
Sanallisesti todettu, että koska derivaatalla ei ole nollakohtia (tarkasteluvälillä), riittää tarkastaa määrittelyvälin päätepisteet (3 p.). TAI Käsitelty funktion kulkua tarkasteluvälillä (hieman vajaavainen käsittely 1 p., huolellinen käsittely 2 p.), todettu, että derivaatan positiivisuudesta seuraa että funktio on kasvava 1 p.
Esimerkkejä perustelusta: Derivaatan merkki testipisteessä ja päättely, esimerkiksi p'(1) =3 *1^2 -2 *1 +1 =2 > 0, joten derivaatta on positiivinen. (Ei pisteitä pelkästä derivaatan arvojen laskemisesta.) TAI Koska derivaatta on ylöspäin aukeava paraabeli, jolla ei ole nollakohtia, sen arvot ovat positiivisia.
riippumaton Suurin arvo on p(2) (=2^3 -2^2 +2) =6, ja pienin arvo on p(1) (=1^3 -1^2 +1) =1 (1 p. kummastakin vastauksesta TAI 1 p. jos laskettu p(2) ja p(1).) (2 p.)
Ratkaisukohtaiset erillisohjeet
Havainto p'(x) =3 x^2 -2 x +1 =2 x^2 +(x -1)^2 > 0 osoittaa sekä derivaatan nollakohtien puuttumisen, että derivaatan positiivisuuden samalla kertaa. (max 12 p.)
Löydetty (virheellisesti) derivaatan nollakohtia, esimerkiksi virhe nollakohtien laskemisessa. (3+2+0+2+2) tai (2+3+0+2+2) (max 9 p.)
Tyyppivirhe: p'(x) =3 x^2 -2 x. (2+2+0+2+2) (max 8 p.)
TAI
Esitetty p tarkasteluvälillä kasvavien ja positiivisten komponenttien tulona/summana. Esimerkiksi: p(x) =x^2 (x -1) +x, p(x) =x ((x -1)^2 +x) (1 p.)
Osoitettu, että komponentit (esimerkiksi x^2, x -1 ja x) ovat (tarkasteluvälillä) kasvavia (3 p.)
Osoitettu, että tulon tekijät ovat (tarkasteluvälillä) ei-negatiivisia (3 p.)
Näin ollen p on kasvava. (3 p.)
riippumaton Suurin arvo on p(2) =2^3 -2^2 +2 =6, ja pienin arvo on p(1) =1^3 -1^2 +1 =1. (2 p.)
B-osa
7. Verrannollisuuksia 12 p.
Täydennä virkkeet. Vastauksia ei tarvitse perustella. Oikea vastaus 1–2 p., väärä vastaus 0 p., ei vastausta 0 p. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.
7.1 Täydennä virkkeet. 3 p.
7.1.1 1 p.
- on kääntäen verrannollinen (1 p.)
7.1.2 2 p.
- 100 (2 p.)
7.2 Täydennä virkkeet. 3 p.
7.2.1 1 p.
- ei ole suoraan eikä kääntäen verrannollinen (1 p.)
7.2.2 2 p.
- 72 (2 p.)
7.3 Täydennä virkkeet. 3 p.
7.3.1 1 p.
- on suoraan verrannollinen (1 p.)
7.3.2 2 p.
- 240 (2 p.)
7.4 Täydennä virkkeet. 3 p.
7.4.1 1 p.
- ovat kääntäen verrannolliset (1 p.)
7.4.2 2 p.
- 3,5 (2 p.)
8. Superkuu 12 p.
Kun Kuu on täydenkuun aikaan lähellä kiertoratansa Maata lähimpänä olevaa kohtaa (perigeum), sitä kutsutaan superkuuksi. Tämän vuosisadan suurin superkuu nähdään 6.12.2052, jolloin Kuun keskipisteen etäisyys Maan pinnalta on noin 350.000 kilometriä. Vastaava etäisyys Kuun kiertoradan kauimpana olevaan kohtaan (apogeum) on noin 401.000 kilometriä. Kuinka monta prosenttia suuremmassa kulmassa Kuu näkyy 6.12.2052 verrattuna pienimpään mahdolliseen kulmaan? Kuun säde on 1737 kilometriä.
Tilanteen hahmottaminen
Mallinnettu kulmaa sanallisesti tai kuvan avulla. (Ympyrä ja kaksi suoraa, jotka muistuttavat tangentteja.) (1 p.)
Kuvattu sanallisesti tai piirretty suorakulmainen kolmio. Vaaditaan joko suorakulman merkki tai että tekstistä käy ilmi kolmion suorakulmaisuus. (1 p.)
Joko oikea malli TAI maininta, että likimääräinen malli riittää. (Joko 0 tai 2 p.)
Tarkennus: Oikealla mallilla tarkoitetaan, että katselupisteestä piirretään tangentit kuulle, jolloin suorakulmat syntyvät kuun kehäpisteisiin. Likimääräisellä mallilla tarkoitetaan, että suorakulmat ovat kuun keskipisteessä etäisyysjanan ja kuun halkaisijan välillä, ja kuun sivuille tulevat suorat ovat näiden kolmioiden hypotenuusat.
Kulmien laskeminen
ylläolevista riveistä riippumaton piste Superkuun tapaus omaa tilannetta vastaavan trigonometrisen yhtälön avulla (sin(x) =1737 /350.000 TAI tan(x) =1737 /350.000) JA ratkaistu yhtälö (x =0,2843519359... ^@ =0,004962877516...rad TAI x =0,2843484341... ^@ =0,004962816399...rad). (2+1 p.)
Kauimmaisin tapaus omaa tilannetta vastaavan trigonometrisen yhtälön avulla (sin(x) =1737 /401.000 TAI tan(x) =1737 /401.000) JA ratkaistu yhtälö (x =0,2481872324... ^@ =0,004331684369...rad TAI x =0,2481849041... ^@ =0,004331643731...rad). (2+1 p.)
STOP: Seuraavat pisteet vain silloin, jos ratkaisussa on laskettu molempien tapausten kulmat.
Koska halkaisija näkyy kaksinkertaisessa kulmassa kummassakin tapauksessa, tätä ei tarvitse huomioida suhteita vertaillessa TAI kerrottu molempien kulmien suuruudet kahdella. (1 p.)
Kulmien suhde vertailtu prosenttilaskulla
Suhde laskettu oikein (esimerkiksi (0,2843519359... ^@ -0,2481849041... ^@) /(0,2481849041... ^@)) ja saatu ((14,5715406... % ~~) 10 %, 15 % TAI 14,6 %. (vain nämä tarkkuudet) (1 p.)
Ratkaisukohtaiset erillisohjeet
Erikoistapaus: Asteet ja radiaanit sekaisin tai 0,284 astetta muuttuu maagisesti 28,4 asteeseen ja muut vastaavasti, -1 p. (vähennys vain kertaalleen)
Erikoistapaus: Sekoitettu säde ja halkaisija 1+1+0+3+3+1+1 (virhe jo kuvassa) tai 1+1+2+(1+1)+(1+1)+1+1 (virhe vasta laskussa) (max 10 p.)
Erikoistapaus: Vertailtu sivujen pituuksia 1+1+2+0+0+0+0+0+0 (max 4 p.)
Erikoistapaus: Luettu tehtävää väärin ja saatu etäisyyksiksi 350000+1737 ja 401000+1737: 1+1+2+2+2+1+1 (max 10 p.)
Erikoistapaus: Kulmat laskettu eri malleilla (oikea ja likimääräinen) 1+1+0+(2+1)+(2+1)+1+0 (max 9 p.)
TAI (Ohjelmisto)
Mallinnettu molemmat kulmat kuvan avulla tai komennoilla. (2 p.)
Oikea mallinnus (tangentit kuulle) TAI epätarkan mallin selitys. (Joko 0 tai 2 p.)
Kulmien mittaaminen
Kuvan mittakaava vaikuttaa olevan oikein (1 p.)
Mitattu ensimmäinen kulma (1 p.)
Mitattu toinen kulma (1 p.)
Dokumentaatio/komennot
Näkyvissä komennot kulman sivujen (suorien) tuottamiseen (2 p.)
Näkyvissä komennot kulmien tuottamiseen (2 p.)
Kulmia vertailtu prosenttilaskulla
Kulmien suhde laskettu oikein ja saatu ((14,5715406... % ~~) 10 %, 15 % TAI 14,6 % (vain nämä tarkkuudet) (1 p.)
Ratkaisukohtaiset erillisohjeet
Erikoistapaus: Jos ohjelmistoratkaisussa laskettu puolikkailla kulmilla ilman perustelua, niin 2+2+1+0+1+2+2+1 (max 11 p.)
9. Sähkösopimukset 12 p.
Viima on hankkimassa uutta sähkösopimusta. Eräs sähköyhtiö tarjoaa seuraavia sopimuksia:
- kiinteähintainen: 9,80 snt/kWh + 5,99 e/kk
- kiinteähintainen, jossa huomioidaan käyttövaikutus: 8,99 snt/kWh + käyttövaikutus + 3,99 e/kk.
Sähkösopimuksessa B esiintyvä käyttövaikutus (yksikkönä snt/kWh) lasketaan kuukausittain kaavalla X /Y -Z. Tässä X lasketaan kuukauden ajalta tuntikohtaisten sähkönkulutusten s_k ja tuntikohtaisten pörssisähkön hintojen h_k avulla kaavalla
X =s_1 h_1 +s_2 h_2 +… +s_720 h_720.Nimittäjä Y on kuukauden kokonaissähkönkulutus ja Z on tuntikohtaisten pörssisähkön hintojen h_k keskiarvo kuukauden ajalta. Käyttövaikutus voi olla myös negatiivinen.
Viima tarkastelee päätöksensä tueksi syyskuun sähkönkulutustaan. Taulukossa on esitetty syyskuun sähkönkulutus tunneittain sekä tunteja vastaavat pörssisähkön hinnat. Taulukossa otsikkoa seuraavalla rivillä esiintyvät siis muuttujien s_1 ja h_1 arvot, sitä seuraavalla s_2 ja h_2 ja niin edelleen.
Kummalla sopimuksella Viiman syyskuun sähkölasku olisi ollut pienempi?
Kuukauden kokonaiskulutus Y=525\mathrm{,}44 kWh. [1 p.]
Komento Sum(B2:B721) tai SUM(B:B) tai vastaava tai selitys tai laskettu kaikki tuntihinnat. Tämän rivin pisteen voi saada, jos on unohtunut yksi rivi, esimerkiksi Sum(B2:B720) tai on laskenut vain näkyvillä olevat rivit Sum(B2:B350). (1 p.)
Sopimus A
Kokonaiskustannus Y\cdot 0\mathrm{,}098+5\mathrm{,}99 tai [tuntihintojen summa+5\mathrm{,}99] JA (57\mathrm{,}48312 \approx) melko täsmälleen 57{,}48 tai melko täsmälleen 30{,}75 (euron tarkkuus riittää) (1+1 p.)
Sopimus B: Oman rivimäärään tulee olla sama jokaisessa välivaiheessa.
Muuttuja X: oikea idea tai oikea komento omalla rivimäärällä ja oikea vastaus X=2502 (2502\mathrm{,}0138812 senttiä). (1+1 p.)
Pörssisähkön tuntikohtaisten hintojen keskiarvo Z: oikea komento omalla rivimäärällä (720 riviä: 4\mathrm{,}084530 senttiä, 349 riviä: 7\mathrm{,}34421444126074 senttiä). (1 p.)
Käyttövaikutus \frac{X}{Y}-Z laskettu omilla luvuilla. (\frac{2502\mathrm{,}0138812}{525\mathrm{,}44}-4\mathrm{,}084531 \approx 0\mathrm{,}6772192 snt/kWh). (2 p.)
Sopimuksen B kokonaiskustannus Y\cdot \frac{8\mathrm{,}99+0\mathrm{,}6772192}{100}+3\mathrm{,}99 JA (54\mathrm{,}7854\approx) melko täsmälleen 54{,}79 tai melko täsmälleen 30{,}64 (euron tarkkuus riittää) (1+1 p.)
Komennoista ilmenee että joka kohdassa on sama määrä rivejä JA rivien 3 ja 7 vastaukset välillä [50, 60], tällöin oikeasta johtopäätöksestä saa pisteen (oikein laskettuna alkuperäisillä luvuilla: "Sopimus B on halvempi"). (1 p.)
Tehtäväkohtaiset erillisohjeet
GeoGebra 6:ssa taulukosta näkyy vain rivit 1-350. Myöhempiin soluihin voi viitata mutta niitä ei näe.
Rivimäärä 349 joka kohdassa. (max 12 p.)
Rivimäärä 719 ja 348 joka kohdassa. (1+1+(1+0)+(1+1)+1+2+(1+0)+1) (max 10 p.)
Rivimäärä 718 tai 347 joka kohdassa. (0+0+(1+0)+(1+1)+1+2+(1+0)+1) (max 8 p.)
Muu väärä rivimäärä. (0+0+1+2+1+2+0+0) (max 6 p.)
Jos rivimäärä vaihtelee eri suureita laskettaessa, tulkitaan rivimäärän vaihdos uudeksi virheeksi.
Eurot ja sentit sekaisin: ei pisteitä siitä laskutoimituksesta missä virhe esiintyy.
Tehtävän voi ratkaista laskematta kokonaiskustannuksia. (max 12 p.)
Käyttövaikutus kertomatta kokonaiskulutuksella sopimuksen B kustannusta laskettaessa. (1+1+(1+1)+(1+1)+1+2+0+1) (max 10 p.)
Esimerkki LibreOffice Calc:in komennoista riveittäin
\texttt{=SUM(B:B)}
\texttt{=SUM(B:B)*0,098+5,99}
\texttt{=SUMPRODUCT(B:B;C:C)}
\texttt{=AVERAGE(C:C)}
\texttt{=SUMPRODUCT(B:B;C:C)/SUM(B:B)-AVERAGE(C:C)}
\texttt{=SUM(B:B)*(8,99+SUMPRODUCT(B:B;C:C)/SUM(B:B)-AVERAGE(C:C))/100+3,99}
\texttt{=IF(E3<E7;"A";"B")}
Esimerkki 12 p. vastauksesta (Geogebran taulukkolaskenta)
Solussa E2: \texttt{B2:B721} (\{0.65, 0.65, 0.42 \ldots)
Solussa E3: \texttt{C2:C721} (\{11.66, 2.5, 2.45 \ldots)
Solussa E4: \texttt{Summa(E2)} (525.44)
Solussa E5: \texttt{E4 * 0.098 + 5.99} (57.48)
Solussa E6: \texttt{Summa(E2 * E3)} (2502.01)
Solussa E7: \texttt{keskar(E3)} (4.08)
Solussa E8: \texttt{E6/E4-E7} (0.68)
Solussa E9: \texttt{E4*(8.99+E8)/100+3.99} (54.79)
Solussa E10: \texttt{Jos(E5 < E9, "A", "B")} (B)
10. Koulutus 18 p.
Yksi kestävän kehityksen tavoitteista (SDG Tavoite 4.1, lyhenne sanoista Sustainable Development Goal) on tarjota riittävä koulutus mahdollisimman monille ihmisille. Eräs tapa arvioida tämän tavoitteen toteutumista on tarkastella niiden 25–29-vuotiaiden ihmisten prosenttiosuutta p(t), jotka ovat opiskelleet vähintään 12 vuotta. Prosenttiosuuden p(t) kehitys on esitetty kuvassa , jossa aika t on vuosiluku.
Logistinen malli on eräs tapa ennustaa funktion p(t) arvoja. Sen mukaan
p(t_2) =p(t_1) +c p(t_1) (100 -p(t_1)) (t_2 -t_1),kun c on malliin liittyvä vakio.
- Mallinnetaan ensin korkean tulotason maiden koulutettujen osuutta. Määritä vakion c arvo niin, että alkuarvolla p(1970) =54 logistinen malli antaa tulokseksi p(2018) =84. Nämä luvut on poimittu kuvan käyrästä, jonka otsikko on "High-income". (4 p.)
- Koko maailman tapauksessa saadaan aikaväliä 1970–2018 käyttämällä vakion arvoksi c = 0{,}000404. Kuvassa tämä vastaa käyrää, jonka otsikko on "Global". Laske logistisen mallin mukainen vuoden 2030 prosenttiosuuden ennuste käyttämällä vain yhtä aikaväliä 2018–2030 ja kuvasta poimittua alkuarvoa. Miten hyvin tulos vastaa kuvan mukaista ennustetta vuodelle 2030? (6 p.)
- Minä vuonna osatehtävän 10.2 logistisen mallin mukaan koko maailman koulutettujen osuus p(t) saavuttaa 75 %:n rajan? Tutki tilannetta taulukoimalla prosenttiosuuden kehitystä vuoden välein alkaen vuodesta 2018. (8 p.)
Osatehtävä 10.1
Sijoitettu kaavaan arvoista t_1 =1970, t_2 =2018, p(t_1) =54 ja p(t_2) =84
(84 =54 +c *54(100 -54) *(2018 -1970))
vähintään 2 eri lukua oikeille paikoille (1 p.) ja kaikki oikein (1 p.). (2 p.)
Ratkaistu ohjelmistolla (kuvakaappaus) tai laskemalla c =(p(t_2) -p(t_1))/(p(t_1)(100 -p(t_1)) *(t_2 -t_1) [1 p.]
( =(84 -54) /(54 *(100 -54) *(2018 -1970)) =30 /119.232 =5 /19.872 ~~0,0002516103) ~~ täsmälleen 0,000252. (1 p.)
Osatehtäväkohtaiset erillisohjeet
Vastaukseksi hyväksytään myös tarkat murtolukuarvot.
Osatehtävä 10.2
Kuvaajan mukaan p(2018)=51. (1 p.)
Sijoitettu kaavaan arvoista t_1=2018, t_2=2030, p(t_1)=51 ja c=0{,}000404
vähintään 2 eri lukua oikeille paikoille (1 p.) ja kaikki oikein (1 p.). (2 p.)
p(2030)=51+0\mathrm{,}000404\cdot 51\cdot (100-51)\cdot (2030-2018)=63{,}115152\approx täsmälleen 63. (1 p.)
Mallin hyvyyden arvioinnin pisteitys: (2 p.)
2 pisteen vastaus: Vertailtu tilannetta monesta näkökulmasta ja 61 % osana vertailua TAI 2 %-yksikköä osana vertailua TAI laskelmilla analysoidaan tilannetta tarkemmin (lasketaan esimerkiksi prosentuaalinen virhe).
1 pisteen vastaus: Vertailu ei ole monipuolinen, mutta vertailussa on mukana 61 % tai kyseessä muuten 2 pisteen vastaus, mutta sotkettu prosenttiyksiköt ja prosentit. Vastauksessa saa olla virheellistä terminologiaa.
Osatehtäväkohtaiset erillisohjeet
Valittu väärä käyrä (0+2+0+2) (max 4 p.)
Osatehtävä 10.3
STOP: Jos käytetty muuta kuin tehtävänannossa annettua yleistä logistista mallia tai sijoitettu p:n arvoja vuosien paikalle, niin ei pisteitä osatehtävästä 10.3.
Taulukoitu arvoja vuosittain t_2:n suhteen käyttäen logistista mallia, jossa c=0,000404 JA t_2 - t_1 on yksi vuosi tai t_1 = 2018 tai t_1 = 1970. (2 p.)
Kuvakaappauksesta tai selityksestä ilmenee, miten taulukon luvut lasketaan. (2 p.)
Kuvakaappauksesta näkyy, milloin 75 % ylitetään. (2 p.)
Poimittu vastaukseen oikea vuosi esimerkiksi 2045 tai 2042 tai 2056. Samoista taulukoista hyväksytään poimituiksi myös luvut 2044, 2041 ja 2055 (tulkinta riippuu siitä, mihin kohtaa vuotta mallin tulkitaan toimivan, alkuun vai loppuun). (2 p.)
Osatehtäväkohtaiset erillisohjeet
Osatehtävästä 10.2. periytynyt väärä käyrä. (max 8 p.)
Prosentit näkyvät vain kokonaislukuina, -1 kolmannelta riviltä.
Valittu viereinen vuosi vastaukseksi (esimerkiksi pyöristysvirheen takia), viimeiseltä riviltä 1 p.
Taulukko vaikuttaa oikealta, mutta dokumentaatio puuttuu. (2+0+2+2) ja huonot selitykset -1 (ensimmäiseltä riviltä). (max 5 p.)
Yhtälöstä 75=51+0,000404\cdot51\cdot(100-51)\cdot(x-2018) ratkaistaan x\approx 2042 (0+0+2+2). Jos lisäksi taulukointia, mahdollisesti pisteitä myös kahdelta ensimmäiseltä riviltä.
11. Avaruuslentoja, tekstiviestejä ja muuta mielenkiintoista 18 p.
Kuvassa verrataan kirjeen postimaksua ja tekstiviestin vastaanottamiseen kykenevien yhdysvaltalaisten lukumäärää. Kuvassa verrataan kaupallisten avaruuslentojen ja sosiologian alan tohtorintutkintojen lukumäärää. Vastaa näiden aineistojen perusteella seuraaviin kysymyksiin. Tarvittaessa voit mitata kuvista lukuarvoja sopivassa ohjelmistossa.
- Minkä kahden peräkkäisen vuoden välillä kirjeen postimaksu muuttui eniten? (4 p.)
- Minä vuonna kaupallisten avaruuslentojen lukumäärä on ollut lähimpänä vuosien 1997–2009 keskiarvoa? (8 p.)
- Miten kuvissa ja näkyy muuttujien välinen korrelaatio? Kummassa tapauksessa on perustellumpaa arvioida, että ilmiöiden välillä on syy-seuraussuhde? (6 p.)
Osatehtävä 11.1
Asetettu koko kuvaaja koordinaatistoon TAI osakuva ja perustelu. (1 p.)
Käytetty pisteitä, jotka ovat silmämääräisesti postimaksukäyrän ympyröiden keskellä tai muuten systemaattisesti. (1 p.)
Päättelyssä käytetyt arvot (tarkkuus kaksi merkitsevää numeroa) näkyvissä kaikkien pisteiden/välien osalta TAI kolmen relevantin osalta ja selitys, miksi nämä riittävät. (1 p.)
Päätelty edellisistä, että suurin muutos on tapahtunut vuosien 2006 ja 2007 välillä TAI vuosien 2008 ja 2009 välillä. (1 p.)
Osatehtäväkohtaiset erillisohjeet
Alkupiste: vedottu silmämääräiseen käyrän jyrkkyyteen ja vastaus 2006–2007 tai 2008–2009. (1 p.)
Pelkkä vastaus. (0 p.)
Osatehtävä 11.2
Asetettu koko kuvaaja koordinaatistoon. (1 p.)
Ohjelmistossa pisteet määritetty/nimetty TAI y-akselin asteikko näkyvissä. (1 p.)
Kaikki y-koordinaatit luettu tai näkyvissä (esimerkiksi algebraikkunassa) silmämääräisesti avaruuskäyrän ympyröiden sisältä JA tarkkuus vähintään kaksi merkitsevää numeroa. (1+1 p.)
Laskettu keskiarvo y-koordinaateista (idea ja lasku oikein). (2 p.)
Verrattu omiin y-koordinaatteihin ja huomattu, että vuoden 2007 (TAI 2006) pisteen y–koordinaatti on lähimpänä. (2 p.)
Osatehtäväkohtaiset erillisohjeet
Pelkkä vastaus (0 p.)
Järkevät y-koordinaatit ilman kuvaa (0+0+1+2+2) (max 5 p.)
Kuvaaja asetettu koordinaatistoon/jonkinlaiset yksikkövaakaviivat löytyvät ja järkevät y-koordinaattien arvot luettu silmämääräisesti koordinaattiruudukon/vaakaviivojen avulla. (1+1+1+2+2) (max 7 p.)
Osatehtävä 11.3
Korrelaatio näkyy kuvassa siinä, että käyrät muuttuvat samansuuntaisesti. [2 p.]
Kun toinen nousee, niin toinenkin nousee, ja kun toinen laskee, niin toinenkin laskee. (1 p.)
riippumaton Syy-seuraussuhde on todennäköisemmin tekstiviestien vastaanottamisen ja kirjeiden hinnan välillä kuin sosiologian alan tohtorintutkintojen ja avaruuslentojen välillä. (1 p.)
riippumaton Sosiologian tohtorintutkintojen ja avaruuslentojen välillä ei ole mitään ilmeistä yhteistä tekijää. (1 p.)
riippumaton On mahdollista, että kirjeiden hintojen kallistuminen on kannustanut ihmisiä lähettämään tekstiviestejä TAI että tekstiviestien yleistyminen on vähentänyt kirjeliikennettä, mikä puolestaan on nostanut kirjeiden postittamisen hintoja. (1 p.)
Osatehtäväkohtaiset erillisohjeet
y-koordinaattiparit lähes suoralla/korrelaatiokertoimet laskettu eikä viittausta kuvaajiin (1+3). (max 4 p.)
Tehtäväkohtaiset erillisohjeet
Jos osatehtävissä 1 ja 2 on argumentoitu, että tehtävää ei voida ratkaista, koska ei tiedetä, onko asteikko lineaarinen vai esimerkiksi logaritminen, niin tämä on pätevä ratkaisu. Sen sijaan argumentiksi ei kelpaa esimerkiksi "y-akselia ei näy, joten ei voi ratkaista".