Beskrivningar av goda svar: SV – Matematik, kort lärokurs
19.3.2025
Slutgiltiga beskrivningar av goda svar 13.5.2025
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
Av en god prestation framgår det hur examinanden har kommit fram till svaret. I lösningen måste det ingå nödvändiga uträkningar eller andra tillräckliga motiveringar och ett slutresultat. I bedömningen fästs uppmärksamhet vid helheten och vid de tre stegen start, mellansteg och slutresultat. Räknefel som inte väsentligt ändrar uppgiftens natur ger ingen betydande sänkning av antalet poäng. Räknefel och fel i den matematiska modellen som ändrar uppgiftens karaktär kan däremot sänka antalet poäng avsevärt.
I provet är matematisk programvara ett hjälpmedel, och dess roll bedöms separat för varje uppgift. Om programvara använts i en uppgift ska det framgå av prestationen. I lösningar av uppgifter som kräver analys räcker det inte enbart med ett svar som erhållits med programvara utan övriga motiveringar. Däremot räcker ett svar som examinanden fått med ett program i allmänhet i rutinberäkningar. Detsamma gäller rutinmässiga delar av mera omfattande uppgifter. Exempel på sådana är omskrivning av uttryck, ekvationslösning samt derivering och integrering av funktioner.
Hur bedömningsanvisningarna ska tolkas
- Strukturen på en anvisning
- I anvisningarna kallas en helhet som avslutas med ett poängantal för en rad.
- Uppdelade poäng i en rad är åtskiljda med /-tecknet. I oklara fall har specificerats från vilken del som man får vilka poäng.
- Det finns ingen specificering om det på raden finns lika många uträkningar som poäng - i så fall ges en poäng per uträkning.
- Om en rad består av en uträkning och en motivering i ord i anknytning till den, så härrör hälften av poängen från uträkningen (avrundande uppåt) och resten från motiveringarna.
- Om det på en rad endast finns en uträkning eller en formel och flera poäng, så får man delpoäng för ett tillräckligt bra försök (till exempel beräkning av derivatan delvis rätt).
- En uträkning eller motivering i parentes på en rad är tilläggsinformation som inte behövs för att ge poäng.
- Examinanden får poäng i hakparentes genom att uppfylla den radens villkor eller villkoret på följande rad, om följande rad är i skick, och det inte framgår explicit att föregående rad har gjorts fel.
- Om inget annat anges, godkänns även en gällande siffra fler eller färre än i anvisningarna.
- I allmänhet drar ett räknefel bort poäng från den rad som felet gäller men man kan få de följande radernas poäng om man gör uträkningarna/slutledningarna korrekt för de egna talen. Undantag är betecknade med texten exakt. Man får dessa poäng endast om detta steg och även de föregående stegen är korrekt utförda. Observera att texten exakt betyder att alla de till dessa föregående rader, som inte är oberoende, inklusive motiveringar behöver vara i skick. (Då ska lösningen bestå av korrekt tal eller uttryck eller motsvarande så när som på den ekvivalenta utformningen.) Det här påverkar inte utdelningen av poäng för avrundningar. Om det till exempel står exakt 37, på svarsraden så duger också 37{,}5 och 40. Texten ganska exakt betyder att talen och uträkningarna måste vara i skick, men att det kan finnas brister i motiveringar och förklaringar.
- Radernas beroende av varandra
- I allmänhet är poänganvisningen skriven enligt lösingens matematiska progression och (fulla) poäng ges bara för motiverade steg. Om raderna är uppenbart oberoende av varandra (till exempel om derivatorna till olika funktioner har beräknats) ges poängen oberoende av prestationsordning utan särskild notering.
- Om svaret är skrivet före motiveringarna betyder det att man redan får poäng för blott det korrekta svaret.
- Beteckningen poäng oberoende av de ovanstående raderna betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter denna rad på normalt sätt.
- Beteckningen oberoende betyder att radens poäng kan ges oberoende av de tidigare raderna; de följande raderna förutsätter inte denna rad.
- Beteckningen som slutsats: poängterar att man får ifrågavarande poäng enbart om de tidigare motiveringarna är i skick.
- Ordet STOP betyder att raden beskriver villkor som måste uppfyllas för att kunna få poäng för den fortsatta lösningen.
- Terminologi
- "Svar räcker" betyder att man kan få poäng för korrekt svar även utan motiveringar. Om svaret är felaktigt så kan man få poäng på basis av motiveringar enligt normala principer.
- "Startpoäng" betyder att man härifrån kan ge radens poäng om examinanden inte får poäng från annat håll. Denna poäng kan alltså inte kombineras med andra poäng.
- "maxN" betyder att för en lösning av denna typ ges N poäng om det inte finns andra fel i lösningen.
- "Svaret endast som närmevärde" betyder att svarets exakta värde inte alls framgår i lösningen.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. På ett ställe kan man tillämpa flera avdrag, men man kan inte förlora intjänade poäng.
- Svaret korrekt, men inte i den efterfrågade formen (till exempel noggrannhet, enhet) -1 p.
- Svaret är inte förenklat till slut i en förenklingsuppgift (till exempel e^1, \ln(e) eller 4^0) -2 p.
- Svaret är oförenklat i en annan uppgift (till exempel e^1, \ln(e) eller 4^0) -1 p.
- Uppenbara inmatningsfel i framställningen (till exempel x=2, y04), eller inmatningsfel som korrigeras direkt på följande rad -0 p.
- Kopieringsfel i svaret -1 p.
- Inga flera gällande siffror i en mellanavrundning än i svaret -1 p.
Följande avdrag är av sekundär betydelse för den uppgiftsspecifika poänganvisningen. I en uppgift kan man tillämpa flera avdrag, men vardera avdrag högst en gång.
- Matematiskt bristfällig beteckning (till exempel parenteser som fattas men korrekt beräknat; =-tecknet använt "i kedja", m^2 utan m). Obs! Beroende på situationen så kan en ostandardiserad beteckning godkännas som förklarad. -1 p.
- I lösningen saknas väsentliga förklaringar (läsaren måste gissa vad talen i lösningen betyder) ELLER motiveringarna och slutledningarna är framställda helt lösryckta (läsaren måste kombinera uttryck från olika delar av lösningen) -1 p.
- Betydande överflödig text eller överflödiga beräkningar i en lösning (läsaren måste dra slutsatser om hur lösningen utformas utifrån den givna informationen) -1 p.
Del A
1. Korta uppgifter 12 p.
I den här uppgiften ska du endast ange svaret utan motiveringar. Du kan endast skriva in ett heltal i svarsfältet.
1.1 Lös ekvationen 5 x -17 =43. 2 p.
- 12 (2 p.)
1.2 Vilket är värdet av uttrycket -7 x^2 +2 x (4 x -1) i punkten x =2? 2 p.
- 0 (2 p.)
1.3 Vilken är riktningskoefficienten för den räta linje som går genom punkterna (-2, -2) och (1, 4) ? 2 p.
- 2 (2 p.)
1.4 Vilken är den konstanta termen för linjen i föregående uppgift? 2 p.
- 2 (2 p.)
1.5 I en likbent triangel ligger basvinklarnas vinkelspetsar i punkterna (1, 1) och (5, 1) i koordinatsystemet. Vilken är x-koordinaten för toppvinkelns vinkelspets? 2 p.
- 3 (2 p.)
1.6 Vilket tal får man då de 50 första positiva udda heltalen adderas, det vill säga vad är 1 +3 +… +97 +99? 2 p.
- 2500 (2 p.)
2. Ekvation och talföljd 12 p.
- Lös ekvationen (x+3)(2x-1)=4. (6 p.)
- I en aritmetisk talföljd är det första elementet 2025 och det femte elementet 1973. Vilket är talföljdens hundrade element? (6 p.)
Deluppgift 2.1
Parenteserna korrekt borttagna 2x^2-x+6x-3=4. (1 p.)
STOP: Inga poäng för fortsättningen om ekvationen inte är av andra graden.
Termerna korrekt sammansatta (2x^2+5x-7=0 ELLER 2x^2+5x=7). (1 p.)
Någorlunda ansats till att lösa ekvationen: Satt in tre egna koefficienter (2, 5 och -7), möjligen på fel plats eller med fel tecken. På denna rad godkänns även koefficienterna 2, 5 och -3 från ekvationen 2x^2+5x-3=4. (1 p.)
Samtliga egna koefficienter, vilka svarar mot ekvationens normalform, korrekt insatta x=\frac{-5\pm \sqrt{5^2-4\cdot 2\cdot (-7)}}{2\cdot 2} ELLER infogat skärmdump från SpeedCrunchista, där rätt koefficienter syns. (1 p.)
Den egna diskriminanten förenklad eller rätt behandlad. [1 p.]
Fått korrekta rötter ganska exakt x=1 och x=-\frac{7}{2}. (Decimalformen ganska exakt x=-3,5 godkänns också.) (1 p.)
Särskilda anvisningar för deluppgiften
Fått en ofullständig andragradsekvation, ax^2=b eller ax^2+bx=0. (1+0+1+1+1+0) eller (0+1+1+1+1+0) (max 4 p.)
Startpoäng (1 p.): x=1 eller x=-\frac72 gissat och kontrollerat.
Deluppgift 2.2
(Talföljdens element betecknas a_1, a_2 osv.) Nu gäller a_5-a_1=1973-2025(=-52). Även 2025-1973(=52) fungerar. (1 p.)
Differensen mellan två efterföljande element är alltså -\frac{52}{4}=-13. Rätt idé med division / rätt delare. (2 p.)
Alltså gäller a_{100}=2025-13\cdot 99=738. Rätt idé med subtraktion/ koefficienten 99/ svaret korrekt förenklat. (3 p.)
Särskilda anvisningar för deluppgiften
Typfel: talet 13 oförklarat. (0+0+3) (max 3 p.)
Typfel: talet 13 oförklarat, men visat att det fungerar, till exempel 2025-13-13-13-13=1973. (0+2+3) (max 5 p.)
Startpoäng (1 p.): Rätt idé om den aritmetiska talföljden, till exempel a_{100}=2025+(100-1)d.
3. Mötesarvode 12 p.
Mötesarvodena för de förtroendevalda i en organisation höjdes senast år 2009. År 2023 beslutar organisationen höja sitt mötesarvode från 30 euro till 40 euro. Förtjänstnivåindexet var 2 717 år 2009 och 3 667 år 2023. Kommer höjningen av de förtroendevaldas mötesarvode att överstiga den allmänna förtjänstutvecklingen? Hur stort borde det nya mötesarvodet vara för att höjningen ska följa den allmänna förtjänstutvecklingen?
Förändringskvot för index (se tabell) ELLER kvoten mellan index och arvode med de gamla talen (\frac{2717}{30}\approx90{,}57 ELLER \frac{30}{2717}\approx0{,}0110). (beräkning 3 p., svar 1 p.) (4 p.)
Förändringskvot för arvode (se tabell) ELLER kvoten mellan index och arvode med de nya talen (\frac{3667}{40}=91{,}675 ELLER \frac{40}{3667}\approx0{,}0109). (beräkning 1 p., svar 1 p.) (2 p.)
Förklarat genom att jämföra två tal som är framtagna med rätt logik och sinsemellan jämförbara: de förtroendevaldas arvodeutveckling överstiger inte den allmänna förtjänstutvecklingen. (2 p.)
Med rätt logik beräknat det mötesarvode som svarar mot den allmänna förtjänstutvecklingen (till exempel 30+0\mathrm{,}3497\cdot 30 eller \frac{30}{0{,}7409}) ELLER med förhållandeekvation (till exempel \frac{30}{x}=\frac{2717}{3667}). (2 p.)
Slutsats: Mötesarvodet blir \approx 40{,}49 (euro) (eller 40{,}50 euro eller 40{,}5 euro, endast dessa noggrannheter). (svar 1 p., avrundning 1 p.) (2 p.)
Särskilda anvisningar för uppgiften
Faktor 0{,}3497/nämnare 0{,}7409 med minst denna noggrannhet eller inga avrundningspoäng.
Funnit svaret 40{,}49 eller 40{,}50 eller 40{,}5 euro genom test och kontrollerat (4+2+2+1+2).
Nämnaren 3667 i rad 1: kräver förklaring, annars -1 p. från rad tre.
Beräknat ett indextal som motsvarar 40 euro: 2717\cdot \frac{40}{30}\approx 3623: (4+2+\dots) från de två första raderna. Härifrån kan man dra slutsatsen (4+2+2+\dots).
Beräknat det arvode som motsvarar det nya indexet:
– ingen slutsats (4+0+0+2+2) (max 8 p.)
– dragit slutsatsen (andra raden behövs ej \Rightarrow poäng därifrån, även om arvodet felaktigt) (max 12 p.)
– räknat fel: en faktor kan ge poäng från första eller andra raden.
Beräkningen av faktorerna saknas men talen syns och är förklarade. (max 11 p.)
Endast svar 40{,}49 euro (eller motsvarande) och "40 e arvode överstiger inte den allmänna nivån". (0 p.)
I tabellen nedan listas olika kvoter som kan användas för att dra den sökta slutsatsen. Även andra sådana kvoter från vilken den sökta slutsatsen kan dras ger \max 6 från de två första raderna. Kvoterna behöver inte vara sinsemellan jämförbara.
| Index (4 p.) | Arvode (2 p.) | |
|---|---|---|
| höjning | \frac{3667-2717}{2717}\approx 34\mathrm{,}97\ \%\approx 35\ \% | \frac{40-30}{30}\approx 33\ \% |
| förändringskoefficient | \frac{3667}{2717}\approx 1{,}3497\approx 1{,}35 | \frac{40}{30}\approx 1{,}33 |
| den gamla mindre än den nya | \frac{3667-2717}{3667}\approx 25\mathrm{,}91\ \%\approx 26\ \% | \frac{40-30}{40}= 25\,\% |
| förändringskoefficient från nya till gamla | \frac{2717}{3667}\approx 0\mathrm{,}7409\approx 0{,}74 | \frac{30}{40}=0{,}75 |
4. Ekvationstyper 12 p.
I gymnasiematematiken är det viktigt att kunna skilja potensekvationer och exponentialekvationer från varandra. En förenklad potensekvation kan skrivas i formen x^n=t, och en förenklad exponentialekvation kan skrivas i formen a^x=b. Här är x den obekanta variabeln i båda exempelekvationerna.
- Ge ett exempel på en potensekvation i förenklad form i vilken n\ge 2 och t\neq 0 och som har endast en lösning. Lös även din ekvation. (6 p.)
- Ge ett exempel på en exponentialekvation i förenklad form i vilken a>1 och b>0. Lös även din ekvation. (6 p.)
Deluppgift 4.1
Givit en ekvation på formen x^n=t, där n\geq 2 och t\neq 0. (1 p.)
Den givna ekvationen x^n=t, som är på korrekt form, har exakt en lösning. (1 p.)
STOP: Följande poäng kan endast fås om föregående rader gav 2 poäng.
Givit korrekt lösning till den egna ekvationen. (2 p.)
Ekvationen löst med en fungerande metod. (2 p.)
Särskilda anvisningar för deluppgiften
Typfel: x^2=4 så x=\sqrt{4}=2. (1+0+stop) (max 1 p.)
Typfel: x^2=4 så x=\pm\sqrt{4}=\pm 2. (1+0+stop) (max 1 p.)
Givit korrekt lösning till den egna ekvationen och testat med insättning. (1+1+2+1) (max 5 p.)
Som svar en oändlig decimalutveckling och avrundning. (max 6 p.)
Beteckningsfel, till exempel tagit kvadratrot i stället för kubikrot eller liknande. (Inget avdrag om korrekt förklaring i ord och rottecknet saknar index.) (-1 p.)
Deluppgift 4.2
Givit en ekvation på formen a^x=b med egna tal. (1 p.)
Den givna ekvationen a^x=b uppfyller a>1 och b>0. (1 p.)
STOP: Följande poäng kan endast fås om föregående rader gav 2 poäng.
Givit korrekt lösning till den egna ekvationen. (2 p.)
Ekvationen löst med en fungerande metod ELLER testat lösningen med insättning. (2 p.)
Särskilda anvisningar för deluppgiften
Rapporterat värden på a och b som svarar mot uppgiftsbeskrivningen, men inga termer eller ekvation givna. (+0 p.)
Lösningsmetod saknas (till exempel "6^x=1 så x=0" eller "6^x=6 så x=1"). (1+1+2+0) (max 4 p.)
Båda sidor givna med samma bas (till exempel "6^x=1 så x=0, ty 6^0=1" eller "6^x=6=6^1, så x=1"). (1+1+2+2) (max 6 p.)
Beteckningsfel, till exempel dividerat bort basen på båda sidor. (-1 p.)
Korrekt lösning till den egna ekvationen ger poäng även om lösningen fåtts med felaktiga räkningar eller fel metod.
Typfel: överflödiga minustecken (till exempel -2^x=-8, så x=3). (0 p.)
5. Picks sats 12 p.
Picks sats från 1899 gäller plangeometri och arean på månghörningar. En månghörning är ritad i ett rutnät så att alla hörnpunkter är belägna i skärningspunkterna mellan linjer, det vill säga i gitterpunkter. Enligt satsen kan arean på en viss typ av månghörningar beräknas med formeln
(*)\qquad A = S + \frac{R}2 - 1,
där A är månghörningens area angiven i rutor, S är antalet gitterpunkter som ligger inne i månghörningen och R är antalet gitterpunkter som ligger på månghörningens rand.
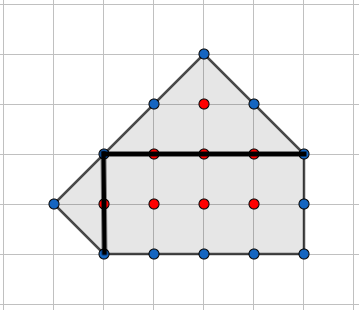
Beräkna figurernas areor och visa att formeln (*) stämmer för planfiguren i fallet , men inte stämmer för planfiguren i fallet .
Deluppgift 5.1
I figur A: S=8, R=12, [1 p.]
så formeln ger arean ganska exakt 8+\frac{12}{2}-1=13. (1 p.)
Figuren delas in exempelvis enligt följande:
Beskrivit en uppdelning av området i beräkningsbara delar med bild eller ord. (1 p.)
Delarna i den egna uppdelningen korrekt beräknade (rektangelns area 2\cdot 4=8 och trianglarnas areor 2\cdot 1\cdot \frac{1}{2}=1 och 4\cdot 2\cdot \frac{1}{2}=4 ELLER det finns 10 hela rutor och 6 halva rutor). (Ett delområde obehandlat eller fel: 1 p., flera delområden: 0 p.) (2 p.)
exakt Slutsats: Arean är alltså 8+1+4=13 ELLER 10+\frac{1}{2}\cdot 6=13, så formeln stämmer. (1 p.)
Särskilda anvisningar för deluppgiften
Rätt area given utan förklaring max 1+1+0+0+0. (max 2 p.)
Rätt area beräknad med ett rimligt uttryck, som inte motiverats alls max 1+1+0+2+0. (max 4 p.)
Deluppgift 5.2
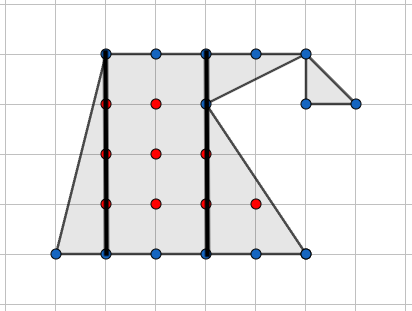
I figur B: S=9, R=14, [1 p.]
så formeln ger arean ganska exakt 9+\frac{14}{2}-1=15. (1 p.)
Figuren delas in exempelvis enligt följande:
Beskrivit en uppdelning av området i beräkningsbara delar med bild eller ord. (1 p.)
Delarna i den egna uppdelningen korrekt beräknade (trianglarnas areor ä 4\cdot 1\cdot \frac{1}{2}=2, 3\cdot 2\cdot \frac{1}{2}=3, 2\cdot 1\cdot \frac{1}{2}=1 och 1\cdot 1\cdot \frac{1}{2}=\frac{1}{2}, rektangelns area är 2\cdot 4=8). (Ett delområde obehandlat eller fel: 1 p., flera delområden: 0 p.) (2 p.)
exakt Slutsats: Arean är alltså 2+3+1+\frac{1}{2}+8=\frac{29}{2}, så formeln stämmer inte. (1 p.)
Särskilda anvisningar för deluppgiften
Rätt area given utan förklaring max 1+1+0+0+0. (max 2 p.)
Rätt area beräknad med ett rimligt uttryck, som inte motiverats alls max 1+1+0+2+0. (max 4 p.)
Särskilda anvisningar för uppgiften
Sista radens poäng i båda deluppgifterna förutsätter att arean är beräknad med motivering och att formelns giltighet/ogiltighet påpekats.
Felaktiga förklaringar till formelns giltighet/ogiltighet. (-0 p.)
Överflödiga (möjligen felaktiga eller orimliga) mätenheter. (-0 p.)
Typisk minimalistisk lösning: A: 13=8+12/2-1, så 13 = 13 och B: 14,5 =9+14/2-1 och 14,5 = 15. (1+1+0+0+0/1+1+0+0+0) (4 p.)
6. Klassiker 12 p.
Bestäm exempelvis med hjälp av derivatan det största och det minsta värdet för polynomfunktionen p(x) =x^3 -x^2 +x , då 1 <= x <= 2.
Derivatan beräknas: p'(x)=3x^2-2x+1. (en term och graden av derivatan rätt 1 p., två termer rätt 1 p., alla termer rätt 1 p.) (3 p.)
Undersöks om den egna derivatan, som är ett andragradspolynom, har nollställen:
x=\frac{2\pm \sqrt{(-2)^2-4\cdot 3\cdot 1}}{2\cdot 3}=\frac{2\pm \sqrt{-8}}{2\cdot 3}. (insättning ungefär rätt 1 p., korrekt satt in tre egna nollskilda termer 1 p., diskriminanten korrekt förenklad [även 4-12 fungerar] 1 p.) (3 p.)
oberoende Diskriminanten är negativ och noterat att derivatan inte har nollställen. (1 p.)
I ord noterat att eftersom derivatan inte har nollställen (på intervallet) så räcker det att kontrollera definitionsintervallets ändpunkter (3 p.). ELLER Behandlat funktionens förlopp på definitionsintervallet (något ofullständig behandling 1 p., fullständig behandling 2 p.), påpekat att eftersom derivatan är positiv så är funktionen växande 1 p.
Exempel på motiveringar: Tecken av derivatan i en testpunkt och dragit slutsats, exempelvis p'(1)=3\cdot1^2-2\cdot 1+1=2>0, så derivatan är positiv. (Inga poäng för att bara ha beräknat derivatans värde.) ELLER Eftersom derivatan är en parabel som öppnar sig uppåt och som inte har nollställen, så är dess värden positiva.
oberoende Största värdet är p(2) \,( =2^3-2^2+2)=6 och minsta värdet är p(1) \, (=1^3-1^2+1)=1. (1 p. för vardera svaret ELLER 1 p. om beräknat p(2) och p(1).) (2 p.)
Särskilda anvisningar för denna lösning
Observationen p'(x)=3x^2-2x+1 = 2x^2 + (x-1)^2>0 visar samtidigt både att derivatan inte har nollställen och att den är positiv. (max 12 p.)
(Felaktigt) funnit nollställen till derivatan, till exempel fel i beräkningen av nollställen. (3+2+0+2+2) eller (2+3+0+2+2) (max 9 p.)
Typfel: p'(x) = 3x^2-2x. (2+2+0+2+2) (max 8 p.)
ELLER
Skrivit p som en produkt eller summa av växande och positiva funktioner på definitionsintervallet. Exempel: p(x)=x^2(x-1)+x, p(x)=x((x-1)^2+x) (1 p.)
Visat att komponenterna (till exempel x^2, x-1 och x) är växande (på definitionsintervallet) (3 p.)
Visat att faktorerna i produkten är icke-negativa (på definitionsintervallet) (3 p.)
Alltså är p växande. (3 p.)
oberoende Största värdet är p(2)=2^3-2^2+2=6 och minsta värdet är p(1)=1^3-1^2+1=1. (2 p.)
Del B
7. Proportionaliteter 12 p.
Komplettera meningarna. Svaren behöver inte motiveras. Korrekt svar 1–2 p., fel svar 0 p., inget svar 0 p. Om du har börjat besvara uppgiften men ändå inte vill lämna in uppgiften för bedömning kan du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn.
7.1 Komplettera meningarna. 3 p.
7.1.1 1 p.
- omvänt proportionell (1 p.)
7.1.2 2 p.
- 100 (2 p.)
7.2 Komplettera meningarna. 3 p.
7.2.1 1 p.
- varken direkt eller omvänt proportionell (1 p.)
7.2.2 2 p.
- 72 (2 p.)
7.3 Komplettera meningarna. 3 p.
7.3.1 1 p.
- direkt proportionellt (1 p.)
7.3.2 2 p.
- 240 (2 p.)
7.4 Komplettera meningarna. 3 p.
7.4.1 1 p.
- är omvänt proportionella (1 p.)
7.4.2 2 p.
- 3,5 (2 p.)
8. Supermåne 12 p.
När månen vid fullmåne är nära den punkt i omloppsbanan som är närmast jorden (perigeum) kallas den supermåne. Den största supermånen i detta århundrade kommer att ses 6.12.2052 då avståndet från jordens yta till månens medelpunkt är cirka 350\,000 kilometer. Motsvarande avstånd till den punkt på månens omloppsbana som är längst bort (apogeum) är cirka 401\,000 kilometer. Under hur många procent större vinkel syns månen 6.12.2052 jämfört med den minsta möjliga vinkeln? Månens radie är 1\,737 kilometer.
Uppfattning av modellen
Modellerat vinkeln med ord eller bild. (Cirkel och två linjer som liknar tangenter.) (1 p.)
Beskrivit med ord eller ritat en rätvinklig triangel. Det krävs att den räta vinkeln antingen markerats i bilden eller nämnts i texten. (1 p.)
Antingen korrekt modell ELLER påpekat att ungefärlig modell räcker. (Antingen 0 eller 2 p.)
Förtydligande: Med korrekt modell menas att man från betraktarens punkt dragit tangenter till månen, med räta vinklar i tangeringspunkterna till månen. Med ungefärlig modell menas att de räta vinklarna är i månens mittpunkt mellan avståndssträckan och månens diameter, och att linjerna från betraktaren till månens sidor är hypotenusor i dessa trianglar.
Beräkning av vinklarna
poäng oberoende av de ovanstående raderna I fallet med supermåne bildat en trigonometrisk ekvation som svarar mot den egna modellen (\sin x = \frac{1737}{350000} ELLER \tan x = \frac{1737}{350000}) OCH löst ekvationen (x= 0\mathrm{,}2843519359\dots ^\circ= 0\mathrm{,}004962877516\dotsrad ELLER x= 0\mathrm{,}2843484341\dots^\circ= 0\mathrm{,}004962816399\dotsrad). (2+1 p.)
I det mest avlägsna fallet bildat en trigonometrisk ekvation som svarar mot den egna modellen (\sin x = \frac{1737}{401000} ELLER \tan x = \frac{1737}{401000}) OCH löst ekvationen (x= 0\mathrm{,}2481872324\dots^\circ= 0\mathrm{,}004331684369\dotsrad ELLER x= 0\mathrm{,}2481849041\dots^\circ= 0\mathrm{,}004331643731\dotsrad). (2+1 p.)
STOP: Följande poäng kan endast fås om lösningen innehåller beräkningar av vinklar i båda fallen.
Eftersom diametern syns med den dubbla vinkeln i båda fallen, behöver man inte ta hänsyn till detta då vinklarna jämförs ELLER multiplicerat båda vinklarna med två. (1 p.)
Bestämt förhållandet mellan vinklarna med procenträkning
Förhållandet rätt beräknat (till exempel \frac{0\mathrm{,}2843519359\dots ^\circ-0\mathrm{,}2481849041\dots^\circ}{0\mathrm{,}2481849041\dots^\circ}) och fått (14\mathrm{,}5715406\dots \% \approx) 10\,\%, 15\,\% ELLER 14{,}6\,\%. (endast dessa noggrannheter) (1 p.)
Särskilda anvisningar för denna lösning
Specialfall: Grader och radianer sammanblandade eller att 0\mathrm{,}284 grader magiskt har ändrats till 28\mathrm{,}4 grader eller motsvarande, -1 p. (avdrag bara en gång)
Specialfall: Blandat ihop radie och diameter 1+1+0+3+3+1+1 (fel redan i bilden) eller 1+1+2+(1+1)+(1+1)+1+1 (fel först i beräkningarna) (max 10 p.)
Specialfall: Jämfört sidlängderna 1+1+2+0+0+0+0+0+0 (max 4 p.)
Specialfall: Läst uppgiften fel och fått avstånden 350000+1737 och 401000+1737: 1+1+2+2+2+1+1 (max 10 p.)
Specialfall: Vinklarna beräknade med olika modeller (korrekt och ungefärlig) 1+1+0+(2+1)+(2+1)+1+0 (max 9 p.)
ELLER (Med programvara)
Modellerat båda vinklarna med bild eller kommando. (2 p.)
Korrekt modell (tangenter till månen) ELLER förklaring av en icke-exakt modell. (Joko 0 tai 2 p.)
Mätning av vinklarna
Bildens skala verkar korrekt (1 p.)
Mätt första vinkeln (1 p.)
Mätt andra vinkeln (1 p.)
Dokumentation/kommandon
Kommandon för att skapa sidorna till vinkeln (linjer) synliga (2 p.)
Kommandon för att skapa vinklarna synliga (2 p.)
Bestämt förhållandet mellan vinklarna med procenträkning
Förhållandet mellan vinklarna korrekt uträknat och fått (14\mathrm{,}5715406\dots \% \approx) 10\,\%, 15\,\% ELLER 14{,}6\,\% (endast dessa noggrannheter) (1 p.)
Särskilda anvisningar för denna lösning
Specialfall: Om man i en lösning med programvara räknat med halva vinkeln utan förklaring, så 2+2+1+0+1+2+2+1 (max 11 p.)
9. Elavtal 12 p.
Vilma ska skaffa ett nytt elavtal. Ett elbolag erbjuder följande avtal:
- Avtal med fast pris: 9{,}80 cent/kWh + 5{,}99 euro/mån.
- Avtal med fast pris, där en förbrukningsinverkan beaktas: 8{,}99 cent/kWh + förbrukningsinverkan + 3{,}99 euro/mån.
Förbrukningsinverkan (i cent/kWh) i elavtal B beräknas månadsvis med formeln \frac{X}{Y}-Z. Här beräknas X för en månad med hjälp av elförbrukningen e_k per timme och priset på börsel p_k för respektive timme med formeln
X=e_1p_1+e_2p_2+\dots+e_{720}p_{720}.Nämnaren Y är månadens totala elförbrukning och Z är medelvärdet av börselens timpriser p_k under månaden. Förbrukningsinverkan kan även vara negativ.
Vilma granskar sin elförbrukning i september som stöd för sitt beslut. I tabell presenteras elförbrukningen per timme i september och motsvarande priser på börsel för dessa timmar. I tabellen visas värdena på variablerna e_1 och p_1 på raden under rubriken, på följande rad e_2 och p_2 och så vidare.
Med vilket avtal skulle Vilmas elräkning för september ha varit mindre?
Månadens totalförbrukning Y=525\mathrm{,}44 kWh. [1 p.]
Kommandot Sum(B2:B721) eller SUM(B:B) eller motsvarande eller förklaring eller räknat ut alla timpriser. Poäng från denna rad kan ges om man har glömt en rad, till exempel Sum(B2:B720) eller om man har räknat bara de synliga raderna Sum(B2:B350). (1 p.)
Avtal A
Totalkostnad Y\cdot 0\mathrm{,}098+5\mathrm{,}99 eller [summan av timpriserna summa+5\mathrm{,}99] OCH (57\mathrm{,}48312 \approx) ganska exakt 57{,}48 eller ganska exakt 30{,}75 (en euros noggrannhet räcker) (1+1 p.)
Avtal B: Antalet rader måste vara samma i varje mellanled.
Variabeln X: rätt idé eller rätt kommando med det egna antalet rader och rätt svar X=2502 (2502\mathrm{,}0138812 cent). (1+1 p.)
Medelvärdet av timpriserna för börsel Z: rätt kommando för det egna radantalet (720 rader: 4\mathrm{,}084530 cent, 349 rader: 7\mathrm{,}34421444126074 cent). (1 p.)
Förbrukningsinverkan \frac{X}{Y}-Z beräknat med de egna talen. (\frac{2502\mathrm{,}0138812}{525\mathrm{,}44}-4\mathrm{,}084531 \approx 0\mathrm{,}6772192 cent/kWh). (2 p.)
Totalkostnaden för avtal B: Y\cdot \frac{8\mathrm{,}99+0\mathrm{,}6772192}{100}+3\mathrm{,}99 OCH (54\mathrm{,}7854\approx) ganska exakt 54{,}79 eller ganska exakt 30{,}64 (en euros noggrannhet räcker) (1+1 p.)
Om det av kommandona framgår att båda priserna beräknats med samma antal rader OCH svaren i rad 3 och 7 båda ligger i intervallet [50, 60], så kan man få poäng för att ha dragit rätt slutsats (korrekt räknat med de ursprungliga värdena: "Avtal B är billigare"). (1 p.)
Särskilda anvisningar för uppgiften
I GeoGebra 6 syns i tabellerna endast raderna 1-350. Celler ur senare rader kan anropas, men syns inte.
Antal rader 349 i varje steg. (max 12 p.)
Antal rader 719 eller 348 i varje steg. (1+1+(1+0)+(1+1)+1+2+(1+0)+1) (max 10 p.)
Antal rader 718 eller 347 i varje steg. (0+0+(1+0)+(1+1)+1+2+(1+0)+1) (max 8 p.)
Annat felaktigt radantal. (0+0+1+2+1+2+0+0) (max 6 p.)
Om antalet rader varierar mellan olika steg, tolkas bytet av radantalet som ett nytt fel.
Euro och cent sammanblandade: inga poäng från det beräkningssteg där felet uppstod.
Uppgiften kan lösas utan att man räknar totalkostnaderna. (max 12 p.)
Förbrukningsinverkan inte multiplicerad med totalförbrukningen när man beräknar kostnaden för avtal B. (1+1+(1+1)+(1+1)+1+2+0+1) (max 10 p.)
Radvis exempel på kommentarer för LibreOffice Calc
\texttt{=SUM(B:B)}
\texttt{=SUM(B:B)*0,098+5,99}
\texttt{=SUMPRODUCT(B:B;C:C)}
\texttt{=AVERAGE(C:C)}
\texttt{=SUMPRODUCT(B:B;C:C)/SUM(B:B)-AVERAGE(C:C)}
\texttt{=SUM(B:B)*(8,99+SUMPRODUCT(B:B;C:C)/SUM(B:B)-AVERAGE(C:C))/100+3,99}
\texttt{=IF(E3<E7;"A";"B")}
Exempellösning för 12 p. (Geogebras tabellräkning)
Cell E2: \texttt{B2:B721} (\{0.65, 0.65, 0.42 \ldots)
Cell E3: \texttt{C2:C721} (\{11.66, 2.5, 2.45 \ldots)
Cell E4: \texttt{Summa(E2)} (525.44)
Cell E5: \texttt{E4 * 0.098 + 5.99} (57.48)
Cell E6: \texttt{Summa(E2 * E3)} (2502.01)
Cell E7: \texttt{medel(E3)} (4.08)
Cell E8: \texttt{E6/E4-E7} (0.68)
Cell E9: \texttt{E4*(8.99+E8)/100+3.99} (54.79)
Cell E10: \texttt{Om(E5 < E9, "A", "B")} (B)
10. Utbildning 18 p.
Ett av målen inom hållbar utveckling (SDG Delmål 4.1, förkortning av orden Sustainable Development Goal) är att erbjuda tillräcklig utbildning för så många människor som möjligt. Ett sätt att utvärdera hur det här målet uppfylls är att granska den procentuella andelen p(t) människor i åldern 25–29 år som har studerat i minst 12 år. Utvecklingen av den procentuella andelen p(t) presenteras i figur , där tiden t är årtalet.
Den logistiska modellen är ett sätt att förutspå värdena på funktionen p(t). Enligt den gäller
p(t_2) =p(t_1) +c p(t_1) (100 -p(t_1)) (t_2 -t_1),då c är en konstant som anknyter till modellen.
- Vi gör först en modell för andelen utbildade i de länder där lönenivån är hög. Bestäm värdet på konstanten c så att den logistiska modellen för startvärdet p(1970)=54 ger p(2018)=84 som resultat. Dessa tal är plockade från kurvan med rubriken "High-income" i figur . (4 p.)
- I fallet hela världen får man genom att använda tidsintervallet 1970–2018 värdet c = 0{,}000404 på konstanten. I figur motsvarar detta kurvan med rubriken "Global". Beräkna enligt den logistiska modellen prognosen för den procentuella andelen år 2030 genom att använda endast ett intervall 2018–2030 och det startvärde som plockats från figur . Hur bra motsvarar resultatet den prognos som figur ger för år 2030? (6 p.)
- Vilket år kommer andelen p(t) utbildade människor i hela världen att nå gränsen 75 % enligt den logistiska modellen i deluppgift 10.2? Undersök situationen genom att tabellera utvecklingen av den procentuella andelen år för år med början 2018. (8 p.)
Deluppgift 10.1
Insättning av värdena t_1=1970, t_2=2018, p(t_1)=54 och p(t_2)=84 i formeln
(84=54+c \cdot 54 (100-54) \cdot (2018-1970)):
åtminstone 2 olika tal på rätt plats (1 p.) alla tal på rätt plats (1 p.). (2 p.)
Löst med programvara (skärmdump) eller med räkning c=\frac{p(t_2)-p(t_1)}{p(t_1)(100-p(t_1))(t_2-t_1)} [1 p.]
\big(=\frac{84-54}{54\cdot(100-54)\cdot(2018-1970)} =\frac{30}{119\,232} =\frac{5}{19\,872}\approx 0,0002516103\big) \approx exakt {0{,}000252}. (1 p.)
Särskilda anvisningar för deluppgiften
Även exakta bråktal godkänns som svar.
Deluppgift 10.2
Enligt kurvan p(2018)=51. (1 p.)
Insättning av värdena t_1=2018, t_2=2030, p(t_1)=51 och c=0{,}000404 i formeln:
åtminstone 2 olika tal på rätt plats (1 p.) alla tal på rätt plat (1 p.). (2 p.)
p(2030)=51+0\mathrm{,}000404\cdot 51\cdot (100-51)\cdot (2030-2018)=63{,}115152\approx exakt 63. (1 p.)
Poäng för bedömningen av modellens kvalitet: (2 p.)
2 poängs svar: Jämfört situationen från flera perspektiv och 61 % ingår i jämförelsen ELLER 2 %-enheter ingår i jämförelsen ELLER situationen noggrannare analyserad med räknare (till exempel beräknat procentuellt fel).
1 poängs svar: ensidig jämförelse, men 61 % ingår i jämförelsen ELLER svar som motsvarar ett 2 poängs svar, men där procent och procentenheter sammanblandats. Svaret får lov att innehålla felaktig terminologi.
Särskilda anvisningar för deluppgiften
Valt fel kurva (0+2+0+2) (max 4 p.)
Deluppgift 10.3
STOP: Om någon annan modell har använts än den logistiska som gavs i uppgiftsbeskrivningen, eller om värden på p satts in i årtalens plats, så ges inga poäng för deluppgift 10.3.
Tabellerat årliga värden för t_2 enligt den logistiska modellen, där c=0,000404 OCH t_2 - t_1 är ett år eller t_1 = 2018 eller t_1 = 1970. (2 p.)
Från skärmdump eller förklaringar framgår hur talen i tabellen beräknats. (2 p.)
Skärmdump visar när gränsen 75 % nås. (2 p.)
Hämtat rätt år till svaret till exempel 2045 eller 2042 eller 2056. Från samma tabeller godkänns även de hämtade talen 2044, 2041 och 2055 (tolkningen beror på vilken tid på året modellen antas beskriva, början eller slutet). (2 p.)
Särskilda anvisningar för deluppgiften
Fel kurva ärvd från deluppgift 10.2. (max 8 p.)
Procent synliga bara som heltal, -1 från tredje raden.
Valt året från en intilliggande rad som svar (till exempel på grund av avrundningsfel), från sista raden 1 p.
Tabellen verkar korrekt, men dokumentation saknas. (2+0+2+2) och dåliga förklaringar -1 (från första raden). (max 5 p.)
Från evationen 75=51+0,000404\cdot51\cdot(100-51)\cdot(x-2018) löst ut x\approx 2042 (0+0+2+2). Om dessutom tabellering gjorts, så kan poäng även ges för de två första raderna.
11. Rymdfärder, textmeddelanden och annat intressant 18 p.
I figur jämförs postavgiften för brev och antalet personer i USA som kan ta emot ett textmeddelande. I figur jämförs antalet kommersiella rymdfärder och antalet doktorsexamina i sociologi. Besvara utgående från dessa material följande frågor. Vid behov du kan mäta talvärdena i figurerna med en lämplig programvara.
- Mellan vilka två på varandra efterföljande år ändrades postavgiften mest? (4 p.)
- Vilket år var antalet kommersiella rymdfärder närmast medelvärdet av antalen åren 1997–2009? (8 p.)
- På vilket sätt syns korrelationen mellan variablerna i figurerna och ? I vilket fall är det mer motiverat att bedöma att det finns ett orsakssamband mellan fenomenen? (6 p.)
Deluppgift 11.1
Fört in hela figuren i ett koordinatsystem ELLER delfigur och förklaring. (1 p.)
Använt punkter som på ögonmått är i mitten av cirklarna på postavgiftskurvan, eller annars systematiskt. (1 p.)
De värden som används för analysen är synliga (med två gällande siffrors noggrannhet) i alla punkter/intervall ELLER i de tre relevanta intervallen och förklaring varför dessa räcker. (1 p.)
Från ovanstående dragit slutsatsen att den största förändringen skedde mellan åren 2006 och 2007 ELLER mellan åren 2008 och 2009. (1 p.)
Särskilda anvisningar för deluppgiften
Startpoäng: hänvisat till kurvans branthet enligt ögonmått och svar 2006–2007 eller 2008–2009. (1 p.)
Endast svar. (0 p.)
Deluppgift 11.2
Fört in hela figuren i ett koordinatsystem. (1 p.)
Punkterna definierade/betecknade i programvaran ELLER y-axelns skala synlig. (1 p.)
Alla y-koordinater inlästa eller synliga (till exempel i algebrafönstret) och enligt ögonmått från det inre av cirklarna i rymdkurvan OCH noggrannhet minst två gällande siffror. (1+1 p.)
Räknat ut medelvärdet från y-koordinaterna (idé och uträkning rätt). (2 p.)
Jämfört med de egna y-koordinaterna och noterat att y-koordinaten för punkten för år 2007 (ELLER 2006) är närmast. (2 p.)
Särskilda anvisningar för deluppgiften
Endast svar (0 p.)
Rimliga y-koordinater utan bild (0+0+1+2+2) (max 5 p.)
Kurvan insatt i ett koordinatsystem/någon sorts vågräta enhetslinjer dragna och rimliga värden för y-koordinaterna lästa på ögonmått från koordinatrutnätet/de vågräta linjerna. (1+1+1+2+2) (max 7 p.)
Deluppgift 11.3
Korrelationen syns i figurerna genom att kurvorna ändrar sig i samma riktning. [2 p.]
När den ena stiger så stiger också den andra, och när den ena sjunker så sjunker också den andra. (1 p.)
oberoende Ett orsakssamband är troligare mellan mottagna textmeddelanden och brevpriserna än mellan doktorsexamina i sociologi och rymdfärder. (1 p.)
oberoende Det finns inga uppenbara gemensamma faktorer mellan dokrorsexamina i sociologi och rymdresor. (1 p.)
oberoende Det är möjligt att de dyrare priserna för brev har uppmuntrat människor att skicka textmeddelanden ELLER att populariseringen av textmeddelanden minskat brevtrafiken, vilket i sin tur har höjt priserna för att skicka brev. (1 p.)
Särskilda anvisningar för deluppgiften
y-koordinatparen ligger nästan på en linje/korrelationskoefficienter uträknade utan hänvisning till figurerna (1+3). (max 4 p.)
Särskilda anvisningar för uppgiften
Om man i deluppgift 1 och 2 har argumenterat för att uppgiften inte kan lösas eftersom man inte vet om skalan är linjär eller till exempel logaritmisk, så är detta en giltig lösning. Däremot duger det inte som argument att exempelvis säga "y-axeln syns inte, så uppgiften kan inte lösas".