Hyvän vastauksen piirteet: FI – Fysiikka
21.3.2025
Lopulliset hyvän vastauksen piirteet 13.5.2025
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
Yleisinä pisteytyksen linjauksina ovat:
- Jos vastauksessa annettujen merkitsevien numeroiden määrä poikkeaa HVP:ssa kirjatusta, vähennetään jokaisen vastauksen kohdalla yksi piste.
- Jos lopputuloksen yksikkö on väärin tai puuttuu, tulos on väärin.
Osa 1: 20 pisteen tehtävä
1. Monivalintatehtäviä fysiikan eri osa-alueilta 20 p.
Valitse jokaisessa osatehtävässä 1.1–1.10 parhaiten soveltuva vastausvaihtoehto. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
Osatehtävien 1.1–1.3 kuvaajissa on esitetty kappaleen nopeus v ajan t funktiona.
1.1 Millaisessa liikeessä kappale on? 2 p.
- Kappale on tasaisessa liikkeessä. (2 p.)
1.2 Millaisessa liikeessä kappale on? 2 p.
- Kappale on tasaisesti kiihtyvässä liikkeessä. (2 p.)
1.3 Millaisessa liikeessä kappale on? 2 p.
- Kappale on kiihtyvässä liikkeessä. (2 p.)
1.4 Mitä tapahtuu kuvaajaan x:llä merkityllä alueella? 2 p.
- Kiehuminen (2 p.)
1.5 Mitä tapahtuu kuvaajaan y:llä merkityllä alueella? 2 p.
- Nestemäisen aineen lämpeneminen (2 p.)
1.6 Mikä komponenteista (A, B tai C) on vastus? 2 p.
- B (2 p.)
1.7 Mikä komponenteista (A, B tai C) on diodi? 2 p.
- C (2 p.)
1.8 Kitaran kieleen syntyy seisova aalto kuvan esittämällä tavalla. Sen aallonpituus on λ. Kuvaan piirretty etäisyys x on 2 p.
- 1/2 λ. (2 p.)
1.9 Elektroni saapuu nopeudella vec v homogeeniseen sähkökenttään vec E kuvan esittämällä tavalla. Mihin suuntaan elektronin rata kaartuu kentässä? 2 p.
- Kuvassa ylöspäin (2 p.)
1.10 Elektroni saapuu nopeudella vec v homogeeniseen magneettikenttään vec B kuvan esittämällä tavalla. Mihin suuntaan elektronin rata kaartuu kentässä? 2 p.
- Kuvassa kohti katsojaa (2 p.)
Osa 2: 15 pisteen tehtävät
2. Puhelimen akun lataaminen 15 p.
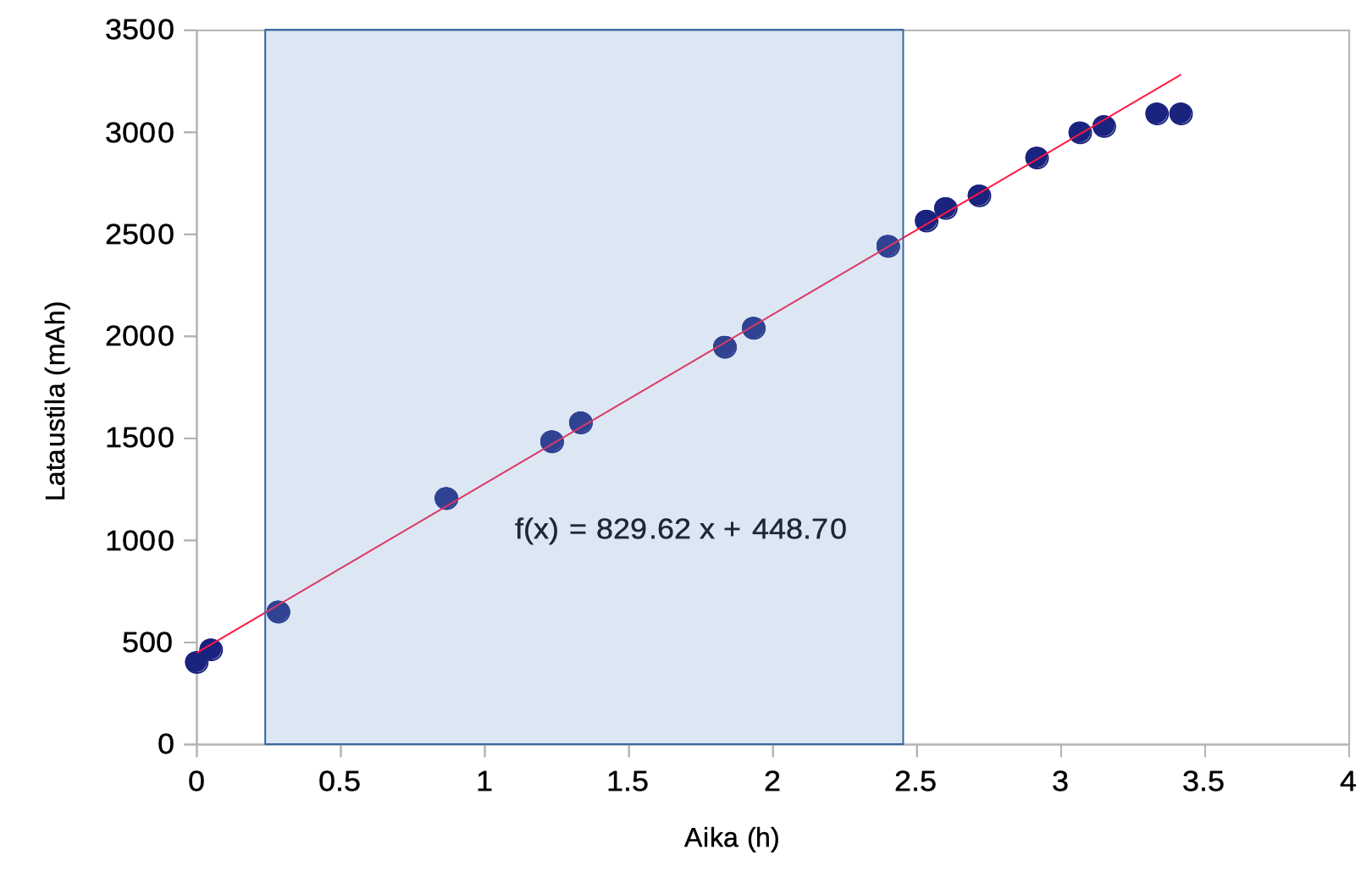
2.1 Taulukossa on esitetty puhelimen akun latausaste latausajan funktiona. Laske latausasteen avulla akun lataustila. Piirrä kuvaaja lataustilasta ajan funktiona. Määritä akkua lataava sähkövirta latausasteen ollessa 20–80 %. Esityksessä tulee näkyä mittaustuloksia vastaavat pisteet, mutta ei pisteitä yhdistäviä viivoja. 7 p.
Akun latausaste 100 % vastaa lataustilaa 3 090 mAh. Tehdään yksikkömuunnos eli kerrotaan taulukon 2.A toinen sarake kertoimella 3090/100 = 30,90, jolloin saadaan lataustila yksiköissä mAh. Myös ajan yksikön voi muuttaa tunneiksi, jolloin latausvirran yksikkö tulee heti oikein suorasovitteesta. Sovitteen perusteella lataava sähkövirta on I = 830 mA = 0,83 A.
Pisteytys:
On esitetty oikea lataustilan kuvaaja ajan funktiona (3 p.)
Kuvaajasta tehdään seuraavat pistevähennykset:
-
Jos on piirretty latausaste, annetaan kuvaajasta nolla pistettä.
-
Jos datapisteet eivät näy kuvaajassa, vähennetään kaksi pistettä.
-
Jos kuvaajaan on piirretty murtoviiva, vähennetään kaksi pistettä.
-
Jos yhden tai molempien akseleiden lukuarvot puuttuvat tai ovat väärin, vähennetään yksi piste.
-
Jos yhden tai molempien akseleiden yksiköt puuttuvat tai ovat väärin, vähennetään yksi piste.
-
Jos yhden tai molempien akseleiden suureen nimi puuttuu tai ovat väärin, vähennetään yksi piste.
-
Jos akselit on piirretty väärin päin, vähennetään yksi piste.
On esitetty oikea lineaarinen sovite kysytylle välille (2 p.)
On annettu oikea sähkövirran arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 0,820 A - 0,833 A (2 p.)
Tyypillisiä virheitä:
On sovitettu suora koko mittausaineistoon.
Sähkövirran arvo on laskettu käyttämällä kahta mittauspistettä.
Virheellisen yksikkömuunnoksen takia on vastattu sähkövirran arvoksi 13,8 Atai 13,8 mA.
2.2 Määritä osatehtävässä 2.1 käytetyn laturin latausteho, kun laturin antama jännite on 5,0 V. 4 p.
Sähköteho on P =U *I joten latausteho on P =4,2 W
Pisteytys:
On esitetty sähkötehon oikea suureyhtälö johon on sijoitettu jännite 5V sekä sähkövirta oikeassa yksikössä (2 p.)
On annettu oikea sähkötehon arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 4,0 W - 4,3 W (2 p.)
2.3 Erään tabletin akun kapasiteetti on 11200 mAh. Tablettia ladataan samalla laturilla ja latausvirralla kuin osatehtävässä 2.1 Kuinka kauan kestää ladata tabletin akku latausasteesta 20 % latausasteeseen 80 %? 4 p.
Tablettiin halutaan ladata Q = (0,80 - 0,20) · 11200 mAh = 6720 mAh. Tähän menee aikaa
t=\frac{Q}{I}=\frac{6,720\,{\rm Ah}}{0,83\,{\rm A}}=8,1\,{\rm h}
Pisteytys:
On esitetty oikea latausajan suureyhtälö johon on sijoitettu varaus ja sähkövirta oikeissa yksiköissä (2 p.)
On annettu ladattavan varauksen 6,72 Ah arvoa käyttämällä oikea latausajan arvo yhdestä kolmeen merkitsevän numeron tarkkuudella välillä 5 h - 20 h ( 2 p.)
Jos latausaika on laskettu käyttämällä virheellisellä yksikkömuunnoksella saatua virran arvoa 13,8 A, annetaan latausajan vastauksesta nolla pistettä.
3. Hehkulamppu uppokuumentimena 15 p.
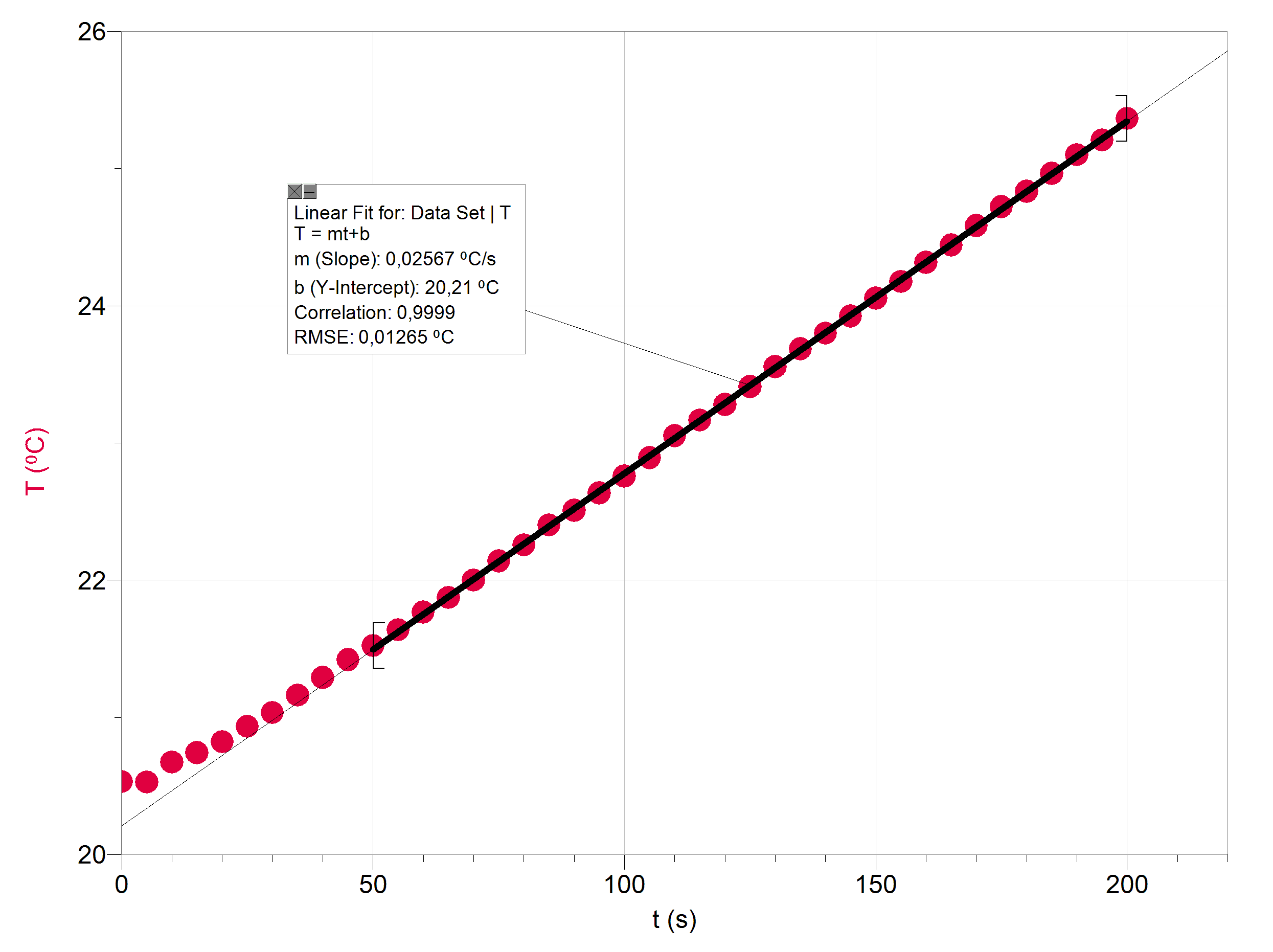
3.1 Laitteella lämmitetään 0,20 litraa vettä. Laadi taulukon mittausaineistosta kuvaaja veden lämpötilasta ajan funktiona. Huomaa, että lämmitys ei ala heti mittauksen alkaessa. Määritä sovitteen avulla veden lämpötilan muutosnopeus aikavälillä 50–200 s. Esityksessä tulee näkyä mittaustuloksia vastaavat pisteet, mutta ei pisteitä yhdistäviä viivoja. 4 p.
Mittausdata ja sovite:
Sovitetun suoran kulmakertoimena saadaan veden lämpötilan muutosnopeus
\frac{\Delta T}{\Delta t} = {\rm 0,02567}\, ^\circ{\rm C/s} \approx {\rm 0,026\, K/s}.
Pisteytys:
On esitetty oikea veden lämpötilan kuvaaja ajan funktiona (2 p.)
Jos kuvaajassa on jokin seuraavista virheistä, annetaan kuvaajasta nolla pistettä:
-
Datapisteet eivät näy kuvaajassa.
-
Kuvaajaan on piirretty murtoviiva.
-
Akselin lukuarvot eivät näy tai ovat väärin.
-
Akselin suuretunnus tai nimi puuttuu tai on väärin.
-
Suureen yksikkö puuttuu tai on väärin.
On esitetty oikea lineaarinen sovite oikealla aikavälillä ja sitä käyttämällä annettu oikea vastaus kahdesta neljään merkitsevän numeron tarkkuudella (2 p.)
Tyypillisiä virheitä:
Lämpötilan muutosnopeus on laskettu kahta datapistettä tai koko mittausaineistoa käyttämällä.
3.2 Kuinka suurella teholla lämpöenergiaa siirtyy veteen? Hyödynnä määrityksessä osatehtävän 3.1 tulosta. 4 p.
Taulukkotietoja:
Veden ominaislämpökapasiteetti c_V =4,19 kJ /(kg K)
Veden tilavuus V =0,20 L
Veden massa m_v = 1,00 kg /L *0,20 L =0,20 kg
Veteen siirtyy energiaa teholla
P_v =Q /(~D t) =c_v m_v (~D T) /(~D t) =c_v m_v *(~D T) /(~D t)
P_v =4,19 kJ /(kg K) *0,20 kg *0,02567 K/s =0,02151146 kJ/s ~~22 W
Pisteytys:
On esitetty oikea tehon suureyhtälö veden massan ja lämpötilan muutosnopeuden avulla (2 p.)
On annettu sovitteen avulla laskettu oikea tehon arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 21 W - 22 W (2 p.)
Tyypillisiä virheitä:
Teho on määritetty käyttämällä alku- ja loppuhetken lämpötilan arvoja.
3.3 Kuinka suurella hyötysuhteella laite lämmittää vettä? 4 p.
Videolta:
Hehkulampun jännite U = 12,00~{\rm V}
Hehkulampun sähkövirta \, I =2,14~{\rm A}
Sähköteho \, P_s = UI = 12,00~{\rm V}\cdot 2,14~{\rm A} = 25,68~{\rm W}
Hyötysuhde, kun syöttöteho on sähköteho ja hyötyteho on veden lämpenemisteho: ~ä =P_v /P_s =(21,51146 W) /(25,68 W) =0,83767368 ~~84 %
Pisteytys:
On annettu sähkötehon suureyhtälö, jonne on sijoitettu oikeat jännitteen ja sähkövirran arvot. Vaihtoehtoisesti kelpaa myös sähkötehon suureyhtälö ja tehon oikea arvo. (2 p.)
On annettu hyötysuhteen oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 0,80 - 0,85 (2 p.)
Tyypilliset virheet:
On laskettu Carnot'n hyötysuhde.
3.4 Minkä syiden vuoksi hyötysuhde ei ole 100 %? Esitä kolme syytä. Oletetaan, että mittausvirheet eivät ole merkittäviä. 3 p.
Laitteen hyötysuhde vedenlämmittimenä on alle 100 %, koska
-
laite lämmittää veden lisäksi myös astiaa, lamppua ja sen kiinnitysosia
-
lämpöeristeestä huolimatta lämpöenergiaa siirtyy pois laitteesta johtumalla kannen ja metallijohtimien läpi
-
osa sähköenergiasta muuntuu sisäenergian kautta säteilyenergiaksi ja laitteen lähettämä terminen säteily, mukaan lukien näkyvä valo, vie mukanaan energiaa.
-
ohmisten tehohäviöiden takia osa sähköenergiasta muuttuu sähköjohdinten lämpöenergiaksi.
Pisteytys:
On esitetty kolme oikeaa syytä (Jokaisesta oikeasta syystä 1 piste, yhteensä 3 pistettä.)
Jos on esitetty enemmän kuin kolme syytä, arvostellaan niistä kolme huonointa.
Tyypillisiä virheitä:
On kerrottu energian karkaavan, katoavan tai häviävän, kertomatta että se siirtyy systeemistä sen ympäristöön.
On esitetty syyksi huono lämpöeristys ilman mainintaa energian siirtymisestä ympäristöön.
On esitetty syyksi mittalaitteiden virheitä.
4. Heliumpallo 15 p.
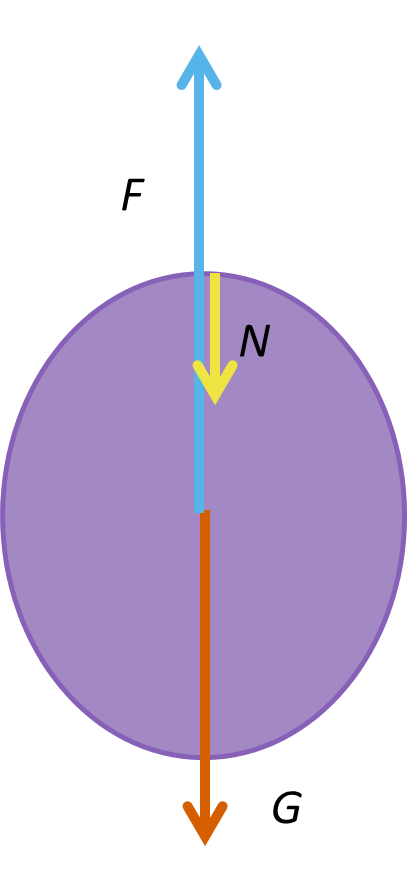
4.1 Heliumilla täytetty pallo on paikallaan huoneen katossa. Piirrä pallon voimakuvio. Voit käyttää kuvaa ratkaisun osana. 5 p.
Pisteytys:
Oikein piirretty voimakuvio, jossa voimat paino (G), tukivoima (N) ja noste (F) on nimetty ja merkitty symbolein (5 p.)
Voimakuviosta tehdään seuraavat pistevähennykset:
-
Vakavasta virheestä (puuttuvat, ylimääräiset tai väärään suuntaan vaikuttavat voimat) vähennetään viisi pistettä.
-
Merkittävistä virheistä (voimien summa eroaa nollasta, yhden tai useamman voiman vaikutuspiste on väärin, useammalla voimalla on sama symboli tai nimi, yhden tai useamman voiman nimi puuttuu) vähennetään kaksi pistettä per virhetyyppi.
-
Jos nopeus- tai kiihtyvyysvektori on piirretty kiinni palloon, vähennetään viisi pistettä
-
Jos ilmanvastus piirretty kuvioon tai nimetty, vähennetään viisi pistettä
4.2 Kuinka suuren voiman katto kohdistaa palloon, kun pallo on paikallaan huoneen katossa? 6 p.
Newtonin II lain mukaan
\Sigma \vec{F} = m\vec{a}
\vec{G}+\vec{N}+\vec{F}=m\vec{a}
Kiihtyvyys on nolla, joten
N-F+G=0
N=\rho_iVg-mg
=\rho_iVg-(m_p+\rho_{He}V)g
=1,29 kg/m^3 *0,0053 m^3 *9,81 m/s^2 -(0,0038 kg +0,178 kg/m^3 *0,0053 m^3) *9,81 m/s^2 =0,02054 N
Alaspäin kohdistuvan tukivoiman suuruus on 21 mN
Pisteytys:
Ratkaisu on perusteltu mainitsemalla pallon olevan tasapainossa. Vaihtoehtoisesti on mainittu Newtonin II laki ja että pallon kiihtyvyys on nolla / pallo on levossa (2 p.)
On esitetty oikea voimien tasapainon suureyhtälö y-suunnassa (2 p.)
On annettu oikea arvo tukivoimalle kahden tai kolmen merkitsevän numeron tarkkuudella välillä 20 mN - 21 mN. (2 p.)
Tyypillisiä virheitä:
-
Heliumkaasun massa on ratkaisussa jätetty huomiotta.
-
Katon tukivoima puuttuu ratkaisusta.
4.3 Pallo vedetään alas lattian tasolle. Sen jälkeen pallosta päästetään irti, jolloin se nousee takaisin huoneen kattoon. Kuvaaja esittää pallon nopeuden ajan funktiona irti päästämisen jälkeen. Kuinka suuri ilmanvastus palloon kohdistuu juuri ennen kuin pallo osuu kattoon? 4 p.
Kuvaajasta nähdään, että pallo liikkuu tasaisella nopeudella ennen osumistaan kattoon. Tällöin voimien summa on nolla ja ilmanvastuksen täytyy voimien tasapainon perusteella olla yhtä suuri kuin osatehtävässä 4.2 laskettu tukivoima eli 21 mN. Voima suuntautuu pallon liikesuuntaa vastaan eli alaspäin.
Pisteytys:
On kerrottu kuvaajaan vedoten, että pallon liike on tasaista (2 p.)
On kerrottu, että ilmanvastus on yhtä suuri kuin osatehtävän 4.2 tukivoima tai on annettu ilmanvastuksen suuruudelle oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 20 mN - 21 mN (2 p.)
5. Nosturi 15 p.
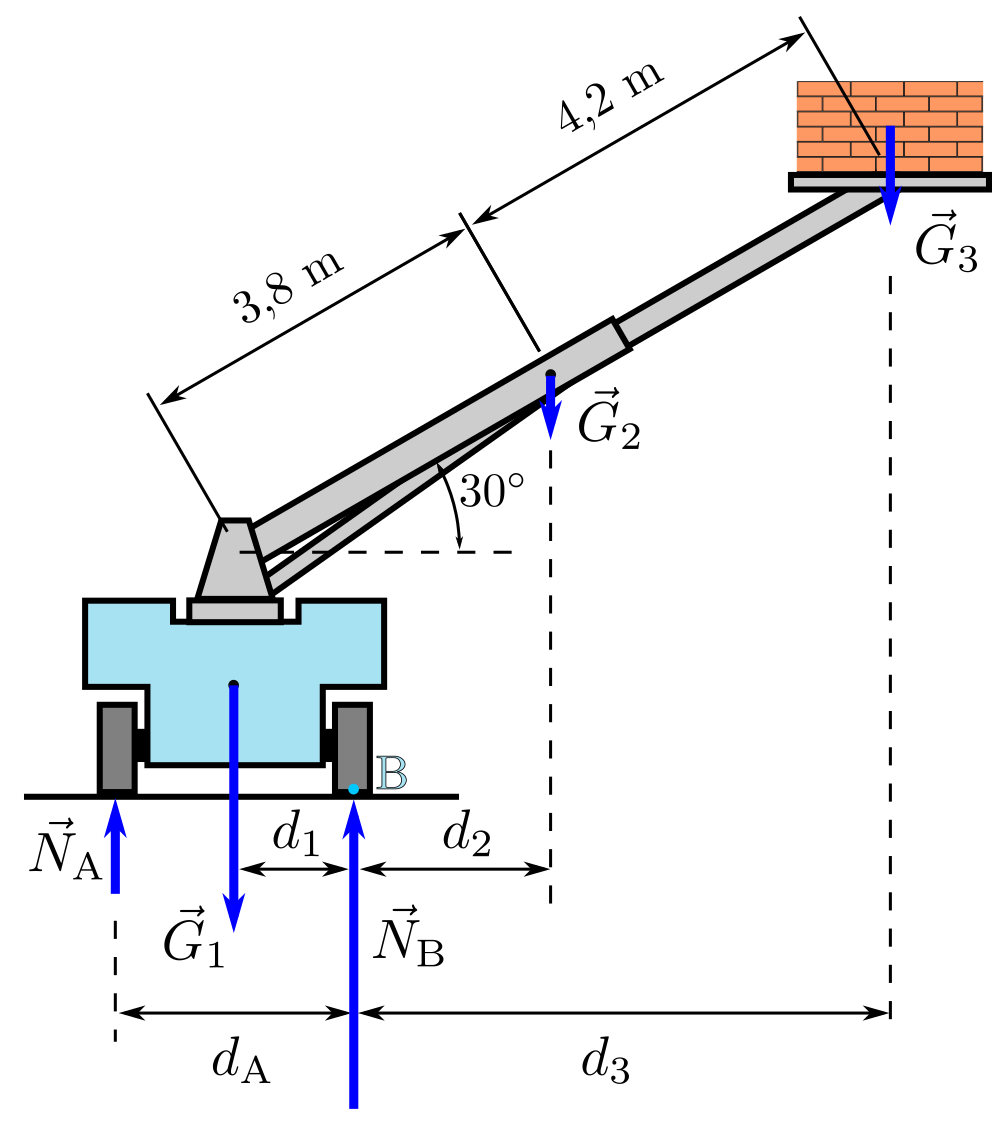
5.1 Kuinka suurilla voimilla telaketjut A ja B kuormittavat maaperää? Voit käyttää voimakuvion piirtämiseen kuvaa . 11 p.
Auton, puomin ja tiilikuorman yhdistelmään vaikuttavat kuvan mukaisesti painovoimat \vec{G}_1, \vec{G}_2 ja \vec{G}_3 ja tukivoimat \vec{N}_{\rm A} ja \vec{N}_{\rm B}. Putoamiskiihtyvyys on g=9,81\,\frac{\rm m}{{\rm s}^2}. Yhdistelmän osien massat ovat m_1=3200\,{\rm kg}, m_2=220\,{\rm kg} ja m_3=320\,{\rm kg} ja painovoimat siten G_1=m_1g=31,39\,{\rm kN}, G_2=m_2g=2,158\,{\rm kN} ja G_3=m_3g=3,139\,{\rm kN}. Valitaan voimien positiivinen suunta ylöspäin. Systeemi on tasapainossa, joten Newtonin II lain mukaan voimien tasapainoehto saadaan muotoon
N_{\rm A}+N_{\rm B}-G_1-G_2-G_3=0.
Kirjoitetaan momenttien tasapainoehto kuvaan merkityn akselin B suhteen. Valitaan momenttien positiivinen suunta myötäpäivään. Voimien varret ovat
d_1=1,4\,{\rm m}
d_2=(3,8\,{\rm m})\cos 30^{\circ}-d_1=1,891\,{\rm m}
d_3=d_2+(4,2\,{\rm m})\cos 30^{\circ}=5,528\,{\rm m}
d_{\rm A}=2d_1=2,8\,{\rm m}.
Momenttien tasapainoehdosta
\Sigma M_{\rm B}=N_{\rm A}d_{\rm A}-G_1d_1+G_2d_2+G_3d_3=0
saadaan telaketjuun A kohdistuva tukivoima
N_A=\frac{G_1d_1-G_2d_2-G_3d_3}{d_A}=8,040\,\rm{kN}\approx 8,0\,\rm{kN}
ja voimien tasapainoehdosta saadaan telaketjuun B kohdistuva tukivoima
N_{\rm B}=G_1+G_2+G_3-N_{\rm A}=28,65\,{\rm kN}\approx 29\,{\rm kN}.
Newtonin III lain perusteella telaketju A kuormittaa maaperää 8,0 kN:n voimalla ja telaketju B 29\,\rm{kN}:n voimalla.
Pisteytys:
On annettu oikein piirretty voimakuvio, jossa voimat on nimetty (3 p.)
Voimakuviolle tehdään seuraavat vähennykset:
-
Jos kuviossa on väärä, puuttuva tai väärään suuntaan vaikuttava voima, vähennetään kolme pistettä
-
Jos tukivoimien keskinäiset pituudet tai painojen keskinäiset pituudet ovat väärin, vähennetään yksi piste
-
Jos yhdellä tai useammalla voimalla on väärä vaikutuspiste, vähennetään yksi piste
-
Jos yhden tai useamman voiman nimi tai symboli puuttuu, vähennetään yksi piste
-
Jos useammalle voimalle käytetty samaa symbolia , vähennetään yksi piste
Ratkaisu on perusteltu mainitsemalla systeemin tasapaino tai Newtonin II laki (1 p.)
On esitetty oikea momenttien tasapainon skalaarimuotoinen suureyhtälö. Ratkaisusta ilmenee käytetty momenttipiste (2 p.)
On esitetty oikea voimien tasapainon skalaarimuotoinen suureyhtälö tai on esitetty toinen oikea momenttien tasapainon skalaarimuotoinen suureyhtälö (2 p.)
On perusteltu oikein maaperään kohdistuvien voimien suuruus voima-vastavoima ajatuksella tai mainittu Newtonin III laki (1 p.)
On annettu kahden tai kolmen merkitsevän numeron tarkkuudella oikea arvo voimalle N_A (1 p.) ja voimalle N_B (1 p.)
5.2 Jos puomia pidennetään liikaa, nosturi kaatuu. Miksi? Mitä osia nosturiin voisi lisätä, jotta se ei kaatuisi? Yksi muutosehdotus riittää. 4 p.
Puomin pidentäminen kasvattaa vec G_2:n ja vec G_3:n varsia d_2 ja d_3 ja edelleen kyseisten voimien momentteja. Jos näiden ”kaatavien” momenttien summa kasvaa suuremmaksi kuin vec G_1:n tasapainottava, vakiona pysyvä momentti, auto kaatuu. Tämä voidaan estää asentamalla autoon tarpeeksi pitkälle kuorman puolelle ulottuvat tukijalat tai sijoittamalla riittävä vastapaino auton toiselle puolelle.
Pisteytys:
On kerrottu, että varren pidentäminen kasvattaa kaatavien voimien momenttien suuruutta tai siirtää systeemin massakeskipisteen tukipinnan ulkopuolelle (2 p.)
Parannusehdotuksena on esitetty joko autoon kiinnitettävät tukijalat tai lisäpainojen asentaminen (2 p.)
Jos on vastattu useampia kuin yksi parannusehdotus, arvostellaan vastauksista huonoin.
Tyypillisiä virheitä:
Parannusehdotukseksi on vastattu puomiin tai kuormaan kiinnitettävä tukijalka.
6. Virtamittarit 15 p.
6.1 Haluat mitata virtapiirissä olevan vastuksen läpi kulkevan sähkövirran. Miten virtamittari tulee kytkeä virtapiiriin? Perustele vastaus Kirchhoffin virtalain avulla. 4 p.
Virtamittari kytketään sarjaan vastuksen kanssa.
Kirchhoffin virtalain mukaan sähkövirta jakautuu virtapiirin eri haaroihin siten, että tiettyyn kohtaan tulevien sähkövirtojen summa on yhtä suuri kuin kohdasta lähtevien sähkövirtojen summa.
Jos virtamittari kytketään virheellisesti rinnan vastuksen kanssa, sähkövirta jakautuu virtamittarin ja vastuksen välillä ja virtamittari mittaa kokonaisvirrasta ainoastaan sen osuuden, joka ei kulje vastuksen läpi.
Kun virtamittari kytketään oikealla tavalla, sarjaan vastuksen kanssa, sähkövirta ei jakaudu virtamittarin ja vastuksen välillä, jolloin yhtä suuri sähkövirta kulkee sekä mittarin että vastuksen läpi.
Pisteytys:
On kerrottu tai graafisesti esitetty oikein, että virtamittari kytketään vastuksen kanssa sarjaan (2 p.)
On kerrottu, että Kirchhoffin virtalain perusteella virtapiirin haarautumispisteessä sähkövirta jakautuu ja sen avulla perusteltu että sarjakytkennästä seuraa samansuuruiset sähkövirrat vastuksessa ja virtamittarissa (2 p.)
Jos kytkentätavalle on annettu muu vastaus kuin sarjaankytkentä, osatehtävästä annetaan nolla pistettä.
Tyypillisiä virheitä:
On väitetty, että virtamittari on kytkettävä vastuksen kanssa rinnan.
6.2 Kuvan mukaisella virtapiirillä voidaan määrittää todellisen virtamittarin sisäinen resistanssi, R_{\rm m}. Piirissä olevan etuvastuksen resistanssi R_0 on paljon suurempi kuin säätövastuksen resistanssi R_{\rm x}, eli R_0\gg R_{\rm x}. Tällöin kokonaissähkövirta, I_0, pysyy vakiona säätövastuksen asetuksesta riippumatta. Johda lauseke virtamittarin läpi kulkevalle sähkövirralle I_0:n, R_{\rm x}:n ja R_{\rm m}:n avulla. 7 p.
Piirissä olevan etuvastuksen resistanssi, R_0, on paljon suurempi kuin säätövastuksen resistanssi, jolloin etuvastus määrää piirissä kulkevan kokonaissähkövirran I_0. Näin ollen voidaan Kirchhoffin lakien avulla tarkistaa kokonaissähkövirran jakautuminen rinnan kytkettyjen säätövastuksen ja mittarin välillä.
Kokonaissähkövirta: I_0=I_{R_{\rm x}}+I, jossa I_{R_{\rm x}} on säätövastuksen läpi kulkeva sähkövirta ja I on virtamittarin läpi kulkeva sähkövirta.
Potentiaalimuutokset säätövastuksella ja mittarilla: U_{R_{\rm x}}=U_{\rm m}, eli R_{\rm x}I_{R_{\rm x}}=R_{\rm m}I, jossa R_{\rm x} on säätövastuksen resistanssi ja R_{\rm m} on mittarin sisäinen resistanssi.
Yhdistämällä nämä yhtälöt saadaan R_{\rm x}(I_0-I)=R_{\rm m}I, josta voidaan ratkaista mittarin läpi kulkeva sähkövirta I=I_0\bigl(\frac{R_{\rm x}}{R_{\rm x}+R_{\rm m}}\bigr).
Pisteytys:
On esitetty oikea Kirchhoffin virtalain mukainen suureyhtälö sähkövirroille piirin haarautumispisteessä (2 p.)
On esitetty oikea Kirchhoffin jännitelain mukainen suureyhtälö tai oikein esitetty, että jännitteet säätövastuksen ja virtamittarin yli ovat yhtä suuria (2 p.)
On annettu oikea suureyhtälö sähkövirralle mittarin läpi (3 p.)
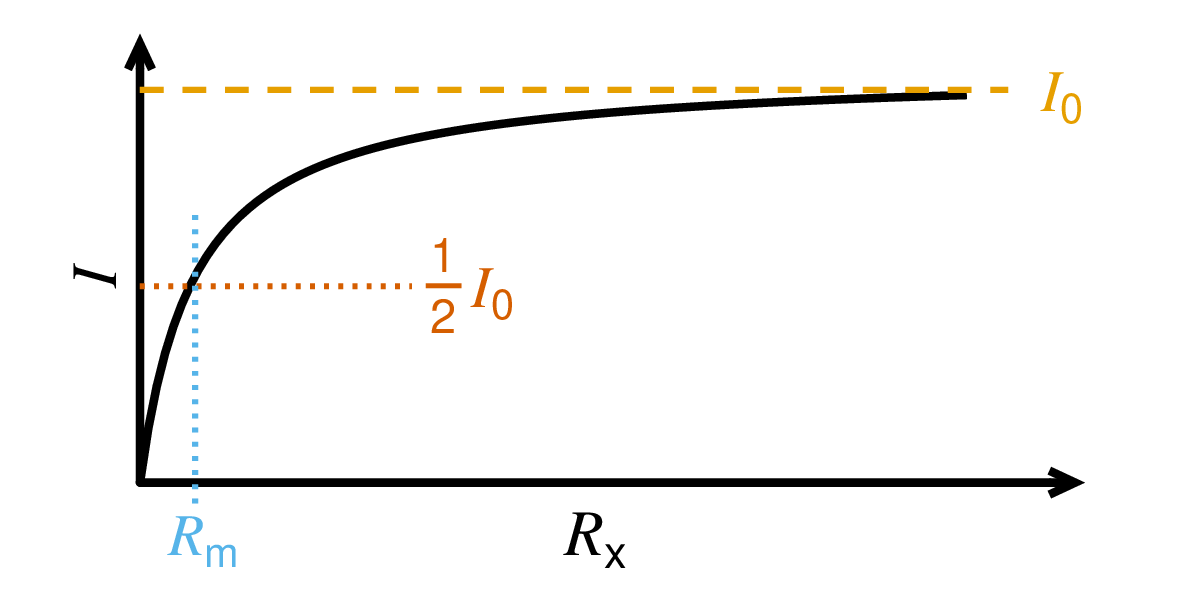
6.3 Kuvan virtapiirissä olevan virtamittarin näyttämä sähkövirran arvo on hahmoteltu säätövastuksen resistanssin funktiona kuvaajassa . Piirissä olevan tasajännitelähteen jännite ja etuvastuksen resistanssi ovat tuntemattomia. Miten voit määrittää kuvaajan avulla virtamittarin sisäisen resistanssin? Lisäksi merkitse kuvaajaan , mistä kohdasta virtamittarin sisäinen resistanssi luetaan ja liitä kuvaaja vastaukseesi. 4 p.
Kun mittarin kanssa rinnan kytketyn säätövastuksen resistanssia säädetään mahdollisimman pieneksi, suurin osa sähkövirrasta kulkee säätövastuksen kautta, jolloin mittarin antama lukema on lähellä nollaa.
Jos säätövastuksen resistanssia säädetään mahdollisimman suureksi, suurin osa sähkövirrasta kulkee mittarin kautta, jolloin mittarin antama lukema on lähellä kokonaissähkövirran arvoa, I0.
Tästä syystä saadaan aineiston mukainen kuvaaja.
Esimerkiksi: Molempien komponenttien kautta kulkee yhtä suuri sähkövirta, kun säätövastuksen resistanssi on säädetty yhtä suureksi kuin virtamittarin sisäinen resistanssi. Virtamittarin sisäinen resistanssi, Rm, voidaan näin ollen lukea säätövastuksen resistanssin arvosta kohdassa, jossa virtamittarin antama arvo on puolet kokonaissähkövirrasta:
Edellisen osatehtävän yhtälöstä voidaan myös huomata, että I=\tfrac{1}{2}I_0, kun R_{\rm x}=R_{\rm m}.
Pisteytys:
On esitetty, että käytetään jotain murto-osaa kokonaisvirrasta ja luetaan säätövastuksen arvo siinä kohdassa (2 p.)
On näytetty kuvaajan avulla, mistä vastuksen arvo luetaan (2 p.)
Jos kuvaajasta on valittu muu arvo sähkövirralle kuin puolet kokonaisvirrasta, on esitettävä suureyhtälö virtamittarin resistanssille, muuten vähennetään kaksi pistettä.
Tyypillisiä virheitä:
Virtamittarin resistanssia on yritetty määrittää käyttämällä kuvaajan kulmakerrointa tai pelkkää kokonaisvirtaa.
7. Valo 15 p.
7.1 Valitse oikea vastausvaihtoehto. 2 p.
- pienempi (2 p.)
7.2 Valitse oikea vastausvaihtoehto. 2 p.
- yhtä suuri (2 p.)
Osatehtävissä 7.3–7.7 sanat, joissa on kirjoitusvirheitä, hyväksytään, jos käy yksikäsitteisesti ilmi, mitä sanalla tarkoitetaan. Vakiintumattomia termejä, jotka ovat muunnelmia vakiintuneista termeistä tai aiheuttavat fysikaalisesti vääriä mielikuvia, ei hyväksytä.
7.3 Täydennä lause kirjoittamalla tyhjään kenttään yksi sana. 2 p.
- aallonpituus (2 p.)
Sanan pitää viitata suureeseen aallonpituus.
7.4 Täydennä lause kirjoittamalla tyhjään kenttään yksi sana. 2 p.
- heijastuminen (2 p.)
Sanan pitää kuvata ilmiötä nimeltä heijastuminen.
7.5 Täydennä lause kirjoittamalla tyhjään kenttään yksi sana. 2 p.
- taittuminen (2 p.)
Sanan pitää kuvata ilmiötä taittuminen.
7.6 Täydennä lause kirjoittamalla tyhjään kenttään yksi sana. 2 p.
- taitekerroin (2 p.)
Sanan pitää viitata suureeseen taitekerroin tai taitesuhde tai taittamiskykyä kuvaavaan ominaisuuteen.
7.7 Täydennä lause kirjoittamalla tyhjään kenttään yksi sana. 3 p.
- taipumiskulma (3 p.)
Sanan pitää viitata taipumisen tai diffraktion aiheuttaman valon suunnanmuutoksen voimakkuuteen tai sitä kuvaavaan suureeseen kuten kulmaan. Myös viittaukset diffraktio- ja taipumisilmiöön hyväksytään.
8. Alfahajoaminen 15 p.
8.1 Kirjoita Rn-222:n alfahajoamisen hajoamisyhtälö. 3 p.
_86^222Rn -> _84^218Po +_2^4He
Pisteytys:
On annettu oikea hajoamisyhtälö (3 p.)
Alfahiukkasesta voi käyttää myös merkintää ~a .
8.2 Miksi radonkaasu aiheuttaa merkittävän säteilyannoksen, vaikka sen lähettämä alfasäteily pysähtyy jo esimerkiksi paperiin? 4 p.
Radon on jalokaasu, joka pääsee hengitysilman seassa keuhkoihin. Keuhkojen kudoksessa ei ole säteilyltä suojaavia solukerroksia kuten ihon pinnalla, joten alfasäteily luovuttaa energiansa suoraan elävään kudokseen ja aiheuttaa siinä säteilyvaurioita.
Pisteytys:
On kerrottu, että radonkaasu kulkeutuu hengityksen mukana keuhkoihin (2 p.)
On kerrottu, että alfahiukkaset luovuttavat energiaansa keuhkokudokseen tai ionisoivat keuhkokudosta (2 p.)
Tyypillisiä virheistä:
-
On ajateltu, että säteilyannoksen suuruus aiheutuu radonin puoliintumisajasta
-
On ajateltu, että alfahiukkaset kulkeutuvat keuhkoihin hengitysilman mukana
8.3 Laske taulukon avulla Rn-222:n alfahajoamisreaktiossa vapautuva energia. Millaisena energiana vapautuva energia ilmenee heti hajoamisen jälkeen? 8 p.
Alfahajoamisen massakato ~D m lasketaan lähtö- ja lopputuotteiden massojen erotuksena. Koska lopputuotteiden yhteenlaskettu massa on pienempi kuin Rn-222:n massa, prosessissa tapahtuu massakatoa eli vapautuu energiaa: Q =~D m c^2
Kaavasta ~D m =m_(Rn) –(m_(Po) +m_(He)) saadaan ~D m =222,017576 u -218,008971 u -4,002603 u ~~0,006002 u ~~9,967 *10^(-30) kg Tässä laskussa on oleellista käyttää He-4-atomin massaa, koska elektronit säilyvät reaktiossa. Jos käyttää alfahiukkasen massaa, sulkulausekkeeseen tulee lisätä kahden elektronin massa.
Kertomalla ~D m valon nopeuden neliöllä saadaan Q =~D m c^2 ~~8,957 *10^-13 J =5,591 MeV Tulos on järkevää pyöristää arvoon 5,59 MeV, vaikka lukuarvoissa on paljon merkitseviä numeroita, sillä massakadon laskukaavassa on lähellä toisiaan olevien arvojen erotus.
Alfahajoamisessa vapautuva energia Q jakautuu alfahiukkasen ja tytärytimen liike-energioiksi.
Pisteytys:
On esitetty massakadon suureyhtälö radonin, poloniumin ja alfahiukkasen massojen avulla tai on annettu massakadon oikea lukuarvo (3 p.)
On annettu vapautuneen energian oikea arvo kahdesta viiteen merkitsevän numeron tarkkuudella välillä 5,550 MeV - 5,620 MeV (3 p.)
Jos massakadon ja vapautuneen energian laskemisessa heliumin massan sijasta on virheellisesti käytetty alfahiukkasen massaa, vähennetään kolme pistettä.
On vastattu, että vapautuva energia ilmenee hajoamistuotteiden liike-energiana (2 p.)
Jos hajoamistuotteiden liike-energian lisäksi mainittu jokin muu energian muoto, energiamuodon tunnistamisesta ei anneta pisteitä.
Tyypillisiä virheitä:
-
Heliumin sijasta massakato määritetään käyttämällä alfahiukkasen massaa
-
On väitetty vapautuvan energian ilmenevän säteilyenergiana
Osa 3: 20 pisteen tehtävät
9. Kaasusylinteri 20 p.
Sylinterissä olevan kaasun tilavuutta, painetta ja lämpötilaa mitataan tietokoneella.
Alkutilanteessa sylinterissä on ilmaa, jonka paine ja lämpötila ovat samat kuin ulkoilman. Mittaus käynnistetään ja mäntä painetaan nopeasti alas. Mäntää pidetään paikallaan alhaalla hetken ja päästetään sitten ponnahtamaan takaisin ylös. Mäntä jää paikalleen yläasentoon. Saadaan kuvassa esitetyt tilavuuden, paineen ja lämpötilan kuvaajat.
Tarkastellaan sylinterissä olevan ilman painetta, lämpötilaa ja sisäenergiaa kokeen eri vaiheissa. Oletetaan, että koetilanteessa ilma käyttäytyy kuten ideaalikaasu.
9.1 Vaihe 1: Mäntä painetaan nopeasti alas. 6 p.
9.1.1 Miten ilman paine käyttäytyy vaiheen 1 mittauksessa? Selitä muiden suureiden mittaustulosten ja tilanteeseen sopivan kaasulain avulla, miksi paine käyttäytyy havaitulla tavalla. 3 p.
Paineen kasvu selittyy ideaalikaasun tilanyhtälöllä p V /T =vakio => p =vakio *T /V
Lämpötila kasvaa ja tilavuus pienenee, joten paine kasvaa.
Pisteytys:
On vastattu että paine kasvaa (1 p.)
Selitys on perusteltu mainitsemalla ideaalikaasun tilanyhtälö (1 p.)
On perusteltu paineen kasvaminen ideaalikaasun tilanyhtälön avulla käyttäen tilavuuden pienentymistä ja lämpötilan kasvua. (1 p.)
Tyypillisiä virheitä:
Paineen suureneminen on perusteltu vain tilavuuden pienenemisellä.
9.1.2 Selitä tilanteeseen sopivan termodynamiikan pääsäännön avulla, kuinka ilman sisäenergia käyttäytyy vaiheessa 1. 3 p.
Tilannetta kuvaa lämpöopin ensimmäinen pääsääntö ~D U =Q +W ilman sisäenergian muutos on yhtä suuri kuin ilman ja ympäristön välillä siirtyvän lämpöenergian ja ilmaan kohdistuvan voiman tekemän työn summa. Männän ilmaan kohdistama voima tekee positiivista työtä. Tilavuuden muutos on nopea, joten lämpöenergiaa ei ehdi siirtyä puristuksen aikana ilmasta pois. Täten Q ~~0 Ilman sisäenergia kasvaa tehdyn työn verran, ~D U =W > 0 Tämä ilmenee ilman lämpötilan nousuna, koska ideaalikaasun sisäenergia on verrannollinen lämpötilaan.
Pisteytys:
On kerrottu että kaasuun tehdään työtä (1 p.)
On kerrottu että kaasusta ei siirry lämpöä (1 p.)
On mainittu termodynamiikan 1. pääsääntö ja perusteltu sen avulla oikein, että kaasun sisäenergia kasvaa kun kaasuun tehdään työtä ja kaasusta ei siirry lämpöä (1 p.)
Tyypillisiä virheitä:
Kaasun sisäenergian muutos on perusteltu vain kaasuun tehdyn työn avulla.
9.2 Vaihe 2: Mäntää pidetään paikallaan alhaalla. 6 p.
9.2.1 Miten ilman lämpötila käyttäytyy vaiheen 2 mittauksessa? Miksi lämpötila käyttäytyy havaitulla tavalla? 3 p.
Lämpötila laskee.
Lämpötilan lasku johtuu termodynaamisen systeemin taipumuksesta hakeutua termiseen tasapainoon (lämpöopin nollas pääsääntö). Kuumasta ilmasta siirtyy lämpöä ympäristöön, koska ilma on kontaktissa huoneen lämpötilassa olevan sylinterin seinämän kanssa. Tällöin ilma jäähtyy. Tilanne kestää tarpeeksi kauan, että ilma ehtii jäähtyä huoneen lämpötilaan.
Pisteytys:
On vastattu että lämpötila laskee (1 p.)
On kerrottu että systeemi hakeutuu termiseen tasapainoon ympäristönsä kanssa (2 p.)
9.2.2 Selitä tilanteeseen sopivan termodynamiikan pääsäännön avulla, kuinka sylinterissä olevan ilman sisäenergia käyttäytyy vaiheessa 2. 3 p.
Mäntä ei liiku, joten ilmaan vaikuttava voima ei tee työtä: W =0 Ilma jäähtyy, joten se luovuttaa energiaa lämpönä. Lämpöopin ensimmäisen pääsäännön mukaan ~D U =Q < 0 ja ilman sisäenergia pienenee.
Pisteytys:
On kerrottu että kaasu ei tee työtä (1 p.)
On kerrottu että kaasusta poistuu lämpöä (1 p.)
On mainittu termodynamiikan 1. pääsääntö ja perusteltu sen avulla oikein, että kaasun sisäenergia pienenee, kun kaasu ei tee työtä ja kaasusta siirtyy pois lämpöä (1 p.)
Jos kaasusta poistuvaa lämpöä on käsitelty tilamuuttujana, osatehtävästä voi saada vain yhden pisteen oikeasta kaasun tekemästä työstä.
Tyypillisiä virheitä:
Kaasun sisäenergian muutos on perusteltu vain kaasusta poistuvan lämmön avulla.
9.3 Vaihe 3: Mäntä päästetään ponnahtamaan ylös. 5 p.
9.3.1 Selitä tilanteeseen sopivan termodynamiikan pääsäännön avulla, kuinka ilman sisäenergia käyttäytyy vaiheessa 3. 3 p.
Tilannetta kuvaa lämpöopin ensimmäinen pääsääntö ~D U =Q +W Nyt ilmaan kohdistuva voima tekee negatiivista työtä, koska voima ja siirtymä ovat vastakkaissuuntaiset. Jälleen tilavuuden muutos on niin nopea, ettei lämpöenergiaa ehdi laajenemisen aikana siirtyä ilmaan, joten Q ~~0 Ilman sisäenergia vähenee tehdyn negatiivisen työn verran, ~D U =W < 0
Pisteytys:
On kerrottu että kaasu tekee työtä (1 p.)
On kerrottu että kaasuun ei siirry lämpöä (1 p.)
On mainittu termodynamiikan 1. pääsääntö ja perusteltu sen avulla oikein, että kaasun sisäenergia pienenee, kun kaasu tekee työtä ja kaasuun ei siirry lämpöä (1 p.)
Tyypillisiä virheitä:
Kaasun sisäenergian muutos on perusteltu vain kaasun tekemän työn avulla.
9.3.2 Miten ilman lämpötila käyttäytyy vaiheen 3 mittauksessa? Miksi lämpötila käyttäytyy havaitulla tavalla? 2 p.
Lämpötila laskee.
Ideaalikaasun sisäenergia on suoraan verrannollinen lämpötilaan. Koska sisäenergia pienenee, ilman lämpötila laskee.
Pisteytys:
On vastattu että lämpötila laskee (1 p.)
Lämpötilan laskeminen on perusteltu oikein kaasun sisäenergian pienenemisellä (1 p.)
9.4 Vaihe 4: Mäntä on palannut yläasentoon ja pysyy paikallaan. 3 p.
9.4.1 Miten paine käyttäytyy vaiheen 4 mittauksessa? Selitä paineen käyttäytyminen muiden suureiden mittaustulosten ja tilanteeseen sopivan kaasulain avulla. 3 p.
Paine kasvaa.
Paineen kasvun selittää jälleen laki p =vakio *T /V.
Paine on aluksi hieman ulkoilman painetta pienempi, koska tilavuus on palannut alkutilanteeseen ja lämpötila on ulkoilman lämpötilaa pienempi. Kun lämpötila nousee huoneen lämpötilaan ja tilavuus pysyy vakiona, myös paine nousee arvoon, jossa se oli mittauksen alkaessa, eli ulkoilman paineeseen.
Pisteytys:
On kerrottu että paine kasvaa tai että paine palaa alkuarvoonsa (1 p.)
Paineen muutos on perusteltu mainitsemalla ideaalikaasun tilanyhtälö tai Gay-Lussacin laki (1 p.)
On kerrottu, että lämpötilan kasvaessa paine kasvaa. Vaihtoehtoisesti on perusteltu paineen palaaminen alkuarvoonsa tilavuuden ja lämpötilan palaamisella alkuarvoihinsa (1 p.)
10. Ulvova ääniputki 20 p.
10.1 Tarkastele putken sisällä olevaa ilmaa. Liikkuuko ilma pyörittäjää kohti, pyörittäjästä poispäin vai edestakaisin? Perustele vastauksesi. 4 p.
Ilmapatsas on periaatteessa täysin vapaa liikkumaan. Kun putkea pyöritetään, ilmapatsas liikkuu herkästi putken sisällä, koska se ei ole sidottu seuraamaan putken seinämän ympyräliikettä. Ilmapatsaan pyörittämiseen tarvittava normaalivoima puuttuu. Tämä johtaa siihen, että ilmapatsas ei pysty seuraamaan putken pyörimistä, vaan valuu putkesta ulos. Ilmavirtauksen suunta on siis kahvasta kohti vapaata päätä. Ilma poistuu vapaasta päästä, ja kahvan kohdalta putkeen tulee korvaavaa ilmaa.
Pisteytys:
On vastattu ilman liikkuvan pyörittäjästä poispäin (2 p.) ja vastaus on perusteltu oikein normaalivoiman puuttumisella (2 p.)
Tyypillisiä virheitä:
On vastattu ilman liikkuvan putkessa edestakaisin.
10.2 Kuvan spektrissä (1) on tunnistettu kolme ominaistaajuutta. Määritä ominaistaajuuksien kertaluvut käyttäen sopivaa fysikaalista mallia. 4 p.
Käytetään molemmista päistä avoimen putken mallia. Perussävelelle putkeen mahtuu puolikas aallonpituus, ensimmäiselle yläsävelelle kokonainen aallonpituus, toiselle yläsävelelle 3/2 aallonpituutta ja niin edelleen. Näin ollen pätee ~l_n =2 L /n jossa L on putken pituus ~l_n on aallonpituus. Perussävelelle n = 1 ja niin edelleen.
Koska v =~l_n f_n jossa v on äänen nopeus ja f_n on aallonpituutta ~l_n vastaava taajuus, saadaan yhdistelemällä kaavoja f_n =n v /(2 L)
Sijoittamalla putken pituudelle ja äänennopeudelle annetut arvot nähdään, että kolme voimakkainta spektrissä (1) näkyvää taajuutta 806 Hz, 1608 Hz ja 2400 Hz vastaavat yläsäveliä n = 4,01, 8,01 ja 11,95, jotka pyöristyvät kokonaisluvuiksi 4, 8 ja 12.
Pisteytys:
Ratkaisu on perusteltu käyttämällä molemmista päistään avoimen putken mallia (2 p.)
On annettu ominaistaajuuksien kertaluvuille vastauksena oikeat kokonaisluvut 4, 8 ja 12 (2 p.)
Oikeiksi vastaukseksi hyväksytään myös oikein lasketut ja nimetyt ylätaajuuksien kertaluvut.
Tyypillisiä virheitä:
Vastauksena on annettu äänen taajuuksia.
10.3 Kun putkea pyöritetään nopeammin, taajuusspektri muuttuu kuvan spektrin (2) mukaiseksi. Määritä ominaistaajuuksien kertaluvut. Laske, paljonko putki on venynyt. 4 p.
Kuvassa 10.B ensimmäinen spektrissä (2) näkyvä voimakas taajuus on kohdassa 1176\,\rm{Hz}.
Tämän lisäksi havaitaan muita yläsäveliä kohdissa 2354 ja 3527 Hz Spektri on siis siirtynyt korkeammille taajuuksille.
Kun avoimen putken mallia sovelletaan kolmelle voimakkaimmalle yläsävelelle, saadaan kaavaa f_n =n v /(2 L) eli n =2 f_n L /v käyttäen yläsävelien kertaluvuille n =5,856 kun f =1176 Hz n =11,722 kun f =2354 Hz ja n =17,563 kun f =3527 Hz
Huomataan, ettei kaava tuota kokonaislukuja yhtä tarkasti kuin edellisessä kohdassa. Tämä voidaan korjata kasvattamalla putken pituutta hieman, koska pituus on suoraan verrannollinen yläsävelen kertalukuun:
L =v n /(2 f_n)
Kaksi ensimmäistä taajuutta ovat hyvin lähellä kokonaislukuja 6 ja 12, ja yläsävelten erotus on noin 1150 Hz mistä päätellään, että kolmas olisi kertaluvultaan n =12 +6 =18 Sijoittamalla nämä kokonaisluvut ja spektristä saadut taajuudet edelliseen lausekkeeseen saadaan
L = 0,875 m (n = 6), L = 0,874256 m (n = 12) ja L = 0,875248 m (n = 18). Putken pituuden pyöristetty keskiarvo on 0,875 m ja venymä näin ollen ~D L =(0,875 -0,854) m =2,1 cm
Pisteytys:
On annettu kertaluvuille vastauksena oikeat kokonaisluvut 6, 12 ja 18 (2 p.)
On annettu putken venymän oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 1,90 cm - 2,30 cm (2 p.)
10.4 Miksi ominaistaajuudet ovat kuvan spektrissä (2) siirtyneet korkeammille taajuuksille? 4 p.
Kun putkea pyöritetään nopeasti, putken seinämän normaalikiihtyvyys kasvaa, ja tarvittaisiin entistä suurempi normaalivoima pitämään ilmaa paikallaan putkessa. Koska normaalivoimaa ei ole, ilmavirtauksen nopeus putken sisällä kasvaa entisestään ja sen myötä myös ryppyjen synnyttämien värähtelyjen taajuudet kasvavat, kun virtausnopeuden kasvun myötä kasvaa myös taajuus, jolla ilmavirta ”törmää” ryppyihin. Putkeen virittyy siis korkeampia yläsäveliä (matalataajuuksisia värähtelyjä ei enää esiinny).
Pisteytys:
On kerrottu että ilmavirtauksen nopeus putkessa kasvaa kun putkea pyöritetään nopeammin (2 p.)
On kerrottu että ilmapatsas törmää ryppyihin useammin kun ilman virtausnopeus on suurempi (2 p.)
Tyypillisiä virheitä:
Taajuuksien siirtyminen korkeammille taajuuksille on perusteltu putken venymisellä.
10.5 Johda lauseke, josta ilmenee, kuinka mones yläsävel putkessa soi, kun putken sisällä virtaavan ilman nopeus on u. 4 p.
Ryppyjen välinen etäisyys olkoon d Kun ilman virtausnopeus putkessa on u ilmavirta törmää peräkkäisiin ryppyihin taajuudella f =u /d
Putkessa siis esiintyy mekaanisia värähtelyjä, joiden taajuus on f Avoimen putken resonanssitaajuudet taas määräytyvät kaavasta f_n =n v /(2 L)
Yhdistelemällä taajuuksien lausekkeet saadaan n v /(2 L) =u /d
Kun kaasuvirtauksen nopeus on u, putkessa soivan äänen kertaluku on n =2 L u /(v d) Tällöin putkessa soi yläsävel m =n -1 =2 L u /(v d) -1.
Pisteytys:
On annettu oikea suureyhtälö taajuudelle, jolla ilmavirta törmää peräkkäisiin ryppyihin (2 p.)
On annettu oikea suureyhtälö yläsävelen kertaluvulle. (2 p.)
Oikeaksi vastaukseksi hyväksytään myös oikein laskettu ja nimetty ominaistajuuden kertaluku.
11. DART-luotain 20 p.
11.1 Laske kiertoajan perusteella kuun ratanopeus ennen törmäystä. 8 p.
Ympyräradan säde voidaan ratanopeuden v ja alkuperäisen kiertoajan T_0 avulla ratkaista yhtälöstä
v =2 ~p r /T_0 => r =v T_0 /(2 ~p)
Kuu (massa M_k) kiertää ympyräradalla asteroidia (massa M_a). Ympyräradalla liikkuvan kuun keskeiskiihtyvyyden aiheuttaa gravitaatiovoima, ja Newtonin II laista seuraa
G M_a M_k /r^2 =M_k v^2 /r
Yhdistämällä yhtälöt ratanopeudeksi saadaan
v =root3(2 ~p G M_a /T_0) =0,176240 m/s ~~17,6 cm/s
Pisteytys:
Ratkaisu on perusteltu mainitsemalla Newtonin II laki (2 p.)
On esitetty kuun kiertoliikettä kuvaava liikeyhtälö, gravitaatiovoiman suureyhtälö kuun ja asteroidin massan avulla sekä keskeiskiihtyvyyden suureyhtälö kiertoajan, ratanopeuden tai kulmanopeuden avulla (2 p.)
On esitetty ratkaistu suureyhtälö kuun nopeudelle tai kuun radan säteelle (2 p.)
On annettu kuun nopeus kahden tai kolmen merkitsevän numeron tarkkuudella välillä 0,17 m/s - 0,18 m/s (2 p.)
11.2 Määritä kuun kiertoajan muutoksen perusteella sen ratanopeuden muutos. 3 p.
Törmäyksen johdosta kuun kiertoaika lyheni arvoon T =11 tuntia ja 22 minuuttia, joten ratanopeuden muutos oli
~D v_(havaittu) =v_(jälkeen) -v_(ennen) =root3(2 ~p G M_a /T) -root3(2 ~p G M_a /T_0) =0,0027979 m/s ~~2,8 mm/s
Pisteytys:
On annettu kuun nopeuden muutoksen oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella (3 p.)
Tyypillisiä virheitä:
Nopeuden muutos on laskettu olettamalla radan säteen pysyvän törmäyksessä ennallaan.
11.3 Laske ennuste ratanopeuden muutokselle täysin kimmottomassa törmäyksessä. Kuinka moninkertainen havaittu ratanopeuden muutos on ennusteeseen verrattuna? 6 p.
Tekstin 11.A kuvassa b)
luotain liikkuu kuun suhteen suurella nopeudella vec v_D. Täysin kimmottomassa törmäyksessä luotain vain uppoaa kuuhun eikä kuun ainesta sinkoudu avaruuteen. Törmäyksen jälkeen kuu ja luotain etenevät kuvan koordinaatistossa molemmat alaspäin nopeudella ~D vec v. Liikemäärän säilymislain perusteella
m_D v_D (M_k +m_D) ~D v
josta kuun nopeuden muutokseksi saadaan
~D v =m_D /(M_k +m_D) v_D =0,0008228 m/s ~~0,82 mm/s
Havaitun nopeuden ja ennustetun nopeuden muutoksen suhde on
~D v_(havaittu) /(~D v) =0,0027979 m/s /(0,0008228) ~~3,4
Kuun nopeuden muutos oli 3,4-kertainen ennusteeseen verrattuna.
Pisteytys:
Ratkaisu on perusteltu mainitsemalla liikemäärän säilyvän törmäyksessä (1 p.)
On esitetty oikea liikemäärän säilymisen suureyhtälö tai ratkaistu oikea suureyhtälö nopeuden muutokselle (2 p.)
On annettu havaitun ja ennustetun nopeuden muutosten suhteelle oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 0,80 mm/s - 0,85 mm/s (2 p.)
On annettu nopeuksien muutosten suhteelle oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella välillä 3,1 - 3,6 (1 p.)
Tyypillisiä virheitä:
On esitetty liikemäärän säilymisen suureyhtälö, jossa kuun nopeutena on ulkopuolisen havaitsijan mittaaman nopeus ja luotaimen nopeutena sen ja kuun suhteellinen nopeus v_D.
11.4 Mistä aiheutuu ennusteen (osatehtävä 11.3) ja havainnon (osatehtävä 11.2) välinen ero? 3 p.
Kun törmäyskokeeseen sovelletaan liikemäärän säilymislakia, pitäisi ottaa huomioon myös kuun pinnalta avaruuteen suurella nopeudella sinkoutuneen aineksen liikemäärä. Jos aineksen liikemäärä on merkittävä ja sen suunta on takaisin luotaimen tulosuuntaan, voi kuun nopeus muuttua paljon enemmän kuin täysin kimmottomassa törmäyksessä.
Pisteytys:
On kerrottu, että liikemäärän säilymislain soveltamisessa pitää huomioida myös avaruuteen sinkoutuneen aineksen liikemäärä (3 p.)
Tyypillisiä virheitä:
Havaitun ja ennustetun nopeuden muutosten ero on perusteltu käyttäen energian säilymislakia.