Beskrivningar av goda svar: SV – Fysik
21.3.2025
Slutgiltiga beskrivningar av goda svar 13.5.2025
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
De allmänna riktlinjerna för poängsättning är:
- Ifall att antalet gällande siffror som ges i svaret avviker från det som anges i BGS är avdraget en poäng för varje svar.
- Om enheten för slutresultatet är felaktig eller saknas är resultatet felaktigt.
Del 1: 20-poängsuppgift
1. Flervalsuppgifter från olika delområden i fysiken 20 p.
Välj det svarsalternativ som passar bäst för varje situation i deluppgifterna 1.1–1.10. Rätt svar ger 2 p., fel svar 0 p. och inget svar 0 p.
Graferna i deluppgifterna 1.1–1.3 visar en kropps hastighet v som funktion av tiden t.
1.1 Vilken typ av rörelse är kroppen i? 2 p.
- Kroppen är i likformig rörelse. (2 p.)
1.2 Vilken typ av rörelse är kroppen i? 2 p.
- Kroppen är i likformigt accelererad rörelse. (2 p.)
1.3 Vilken typ av rörelse är kroppen i? 2 p.
- Kroppen är i accelererad rörelse. (2 p.)
1.4 Vad sker i området som är markerat med x i grafen? 2 p.
- Kokning (2 p.)
1.5 Vad sker i området som är markerat med y i grafen? 2 p.
- Uppvärmning av ett ämne i vätskeform (2 p.)
1.6 Vilken av komponenterna (A, B eller C) är ett motstånd? 2 p.
- B (2 p.)
1.7 Vilken av komponenterna (A, B eller C) är en diod? 2 p.
- C (2 p.)
1.8 En stående våg uppstår i en gitarrsträng på sättet som visas i bilden. Dess våglängd är λ. Avståndet x som är ritat i bilden är 2 p.
- 1/2 λ. (2 p.)
1.9 En elektron anländer med hastigheten \bar v till ett homogent elektriskt fält \bar E på sättet som visas i bilden. I vilken riktning böjer sig elektronens bana i fältet? 2 p.
- Uppåt i bilden (2 p.)
1.10 En elektron anländer med hastigheten \bar v till ett homogent magnetiskt fält \bar B på sättet som visas i bilden. I vilken riktning böjer sig elektronens bana i fältet? 2 p.
- Mot bildens betraktare (2 p.)
Del 2: 15-poängsuppgifter
2. Laddning av ett telefonbatteri 15 p.
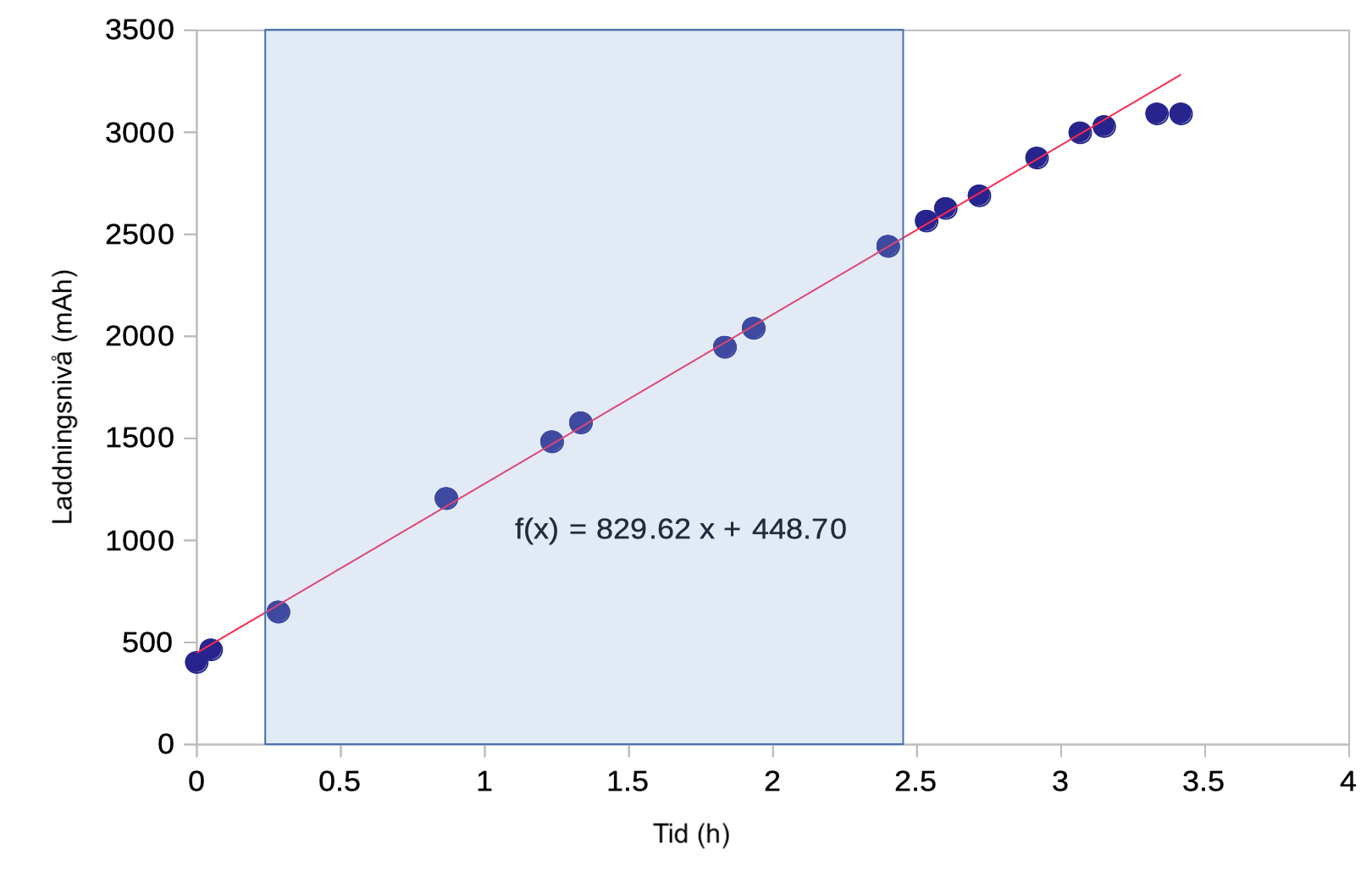
2.1 I tabell presenteras laddningsgraden för telefonens batteri som funktion av laddningstiden. Beräkna batteriets laddningsnivå med hjälp av laddningsgraden. Rita en graf över laddningsnivån som funktion av tiden. Bestäm den elektriska strömmen som laddar batteriet då laddningsgraden är 20–80 %. I den grafiska framställningen ska det visas punkter som motsvarar mätresultaten, men inga streck som sammankopplar punkterna. 7 p.
Laddningsgraden 100 % motsvarar en laddningsnivå på 3 090 mAh för batteriet. Vi gör en enhetsomvandling: andra kolumnen i tabell 2.A multipliceras med faktorn 3090/100 = 30,90, och då får vi laddningsnivån i enheten mAh. Även x-axelns enhet kan omvandlas till timmar. Då blir laddningsströmmens enhet korrekt direkt från anpassningslinjen. Enligt anpassningen är den elektriska strömmen som laddar batteriet I = 830 mA = 0,83 A.
Poängsättning:
Det har presenterats en korrekt graf över laddningsnivån som funktion av tiden. (3 p.)
För grafen görs följande poängavdrag:
-
Ifall laddningsgraden har ritats ges noll poäng för grafen.
-
Om datapunkterna inte syns i grafen är avdraget två poäng.
-
Om en bruten linje har ritats i grafen är avdraget två poäng.
-
Om siffervärdena saknas eller är felaktiga på den ena eller på båda av axlarna är avdraget en poäng.
-
Om enheten saknas eller är felaktig på den ena eller på båda av axlarna är avdraget en poäng.
-
Om storhetens namn saknas eller är felaktig på den ena eller på båda av axlarna är avdraget en poäng.
-
Om axlarna har ritats omvänt är avdraget en poäng.
Den korrekta linjära anpassningen för det efterfrågade intervallet har presenterats. (2 p.)
Rätt värde för den elektriska strömmen har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,820 A - 0,833 A (2 p.)
Typiska fel:
En linje har anpassats till hela mätdata.
Värdet på den elektriska strömmen har beräknats genom att använda två mätpunkter.
På grund av en felaktig enhetsomvandling har det svarats att den elektriska strömmens värde är 13,8 A eller13,8 mA.
2.2 Bestäm laddningseffekten för laddaren som användes i deluppgift 2.1 då spänningen som laddaren ger är 5,0 V. 4 p.
Den elektriska effekten är P=UI alltså är laddningseffekten P =4,2 W
Poängsättning:
Det har presenterats en korrekt storhetsekvation för den elektriska effekten i vilken en spänning på 5 V och en elektrisk ström med korrekt enhet har satts in. (2 p.)
Korrekt värde på den elektriska effekten har med två eller tre gällande siffrors noggrannhet givits inom intervallet 4,0 W - 4,3 W (2 p.)
2.3 Kapaciteten för batteriet i en surfplatta är 11 200 mAh. Surfplattan laddas med samma laddare och samma laddningsström som i deluppgift 2.1. Hur lång tid skulle det ta för surfplattans batteri att laddas från en laddningsgrad på 20 % till en laddningsgrad på 80 %? 4 p.
Surfplattan ska laddas Q = (0,80 - 0,20) · 11 200 mAh = 6720 mAh. För det här krävs tiden
t=\frac{Q}{I} =\frac{6{,}720\,{\rm Ah}}{0{,}83\,{A}}\approx 8{,}1\,{\rm h}
Poängsättning:
Det har presenterats en korrekt storhetsekvation för laddningstiden i vilken en laddning och en elektrisk ström med korrekta enheter har satts in. (2 p.)
Genom att använda ett värde på 6,72 Ah för laddningen som laddas har det korrekta värdet på laddningstiden givits med en till tre gällande siffrors noggrannhet inom intervallet 5 h - 20 h ( 2 p.)
Ifall laddningstiden har beräknats genom att använda värdet 13,8 A som erhållits genom en felaktig enhetsomvandling ges noll poäng för svaret om laddningstiden.
3. En glödlampa som doppvärmare 15 p.
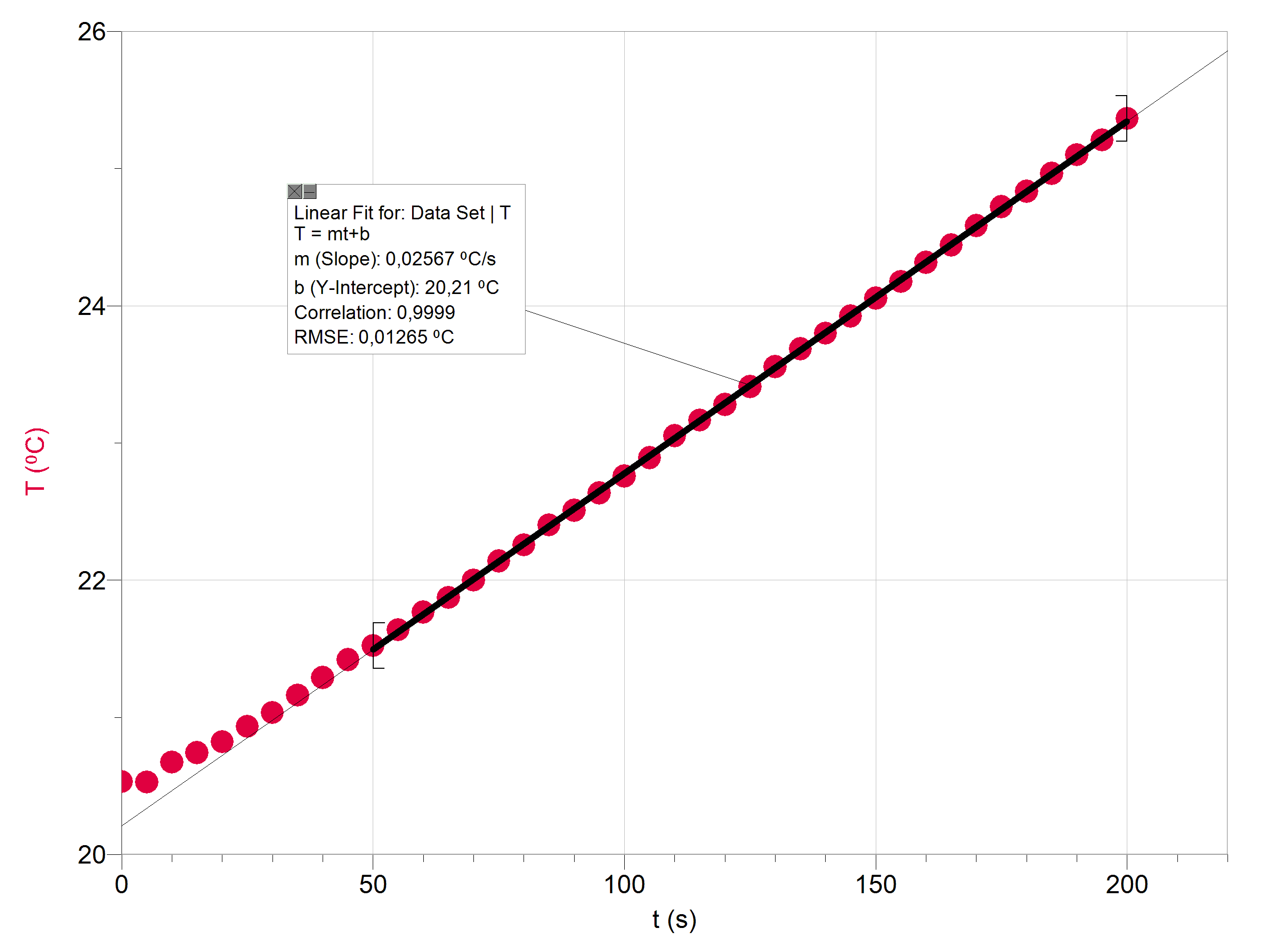
3.1 Anordningen används för att värma 0,20 liter vatten. Gör en graf över vattnets temperatur som funktion av tiden utgående från mätdata i tabell . Notera att uppvärmningen inte startar omedelbart när mätningen inleds. Bestäm med hjälp av en anpassning temperaturens förändringshastighet inom tidsintervallet 50–200 s. I den grafiska framställningen ska det visas punkter som motsvarar mätresultaten, men inga streck som sammankopplar punkterna. 4 p.
Mätdata och anpassning:
Från den anpassade linjens riktningskoefficient får vi temperaturens förändringshastighet för vattnet
\frac{\Delta T}{\Delta t} = {\rm 0,02567}\, ^\circ{\rm C/s} \approx {\rm 0,026\, K/s}.
Poängsättning:
Det har presenterats en korrekt graf över vattnets temperatur som funktion av tiden. (2 p.)
Ifall grafen innehåller något av följande fel ges noll poäng för grafen:
-
Datapunkterna syns inte i grafen.
-
En bruten linje har ritats i grafen.
-
En axels siffervärden syns inte eller är felaktiga.
-
En axels storhetsbeteckning eller namn saknas eller är felaktigt.
-
Enheten för en storhet saknas eller är felaktig.
En korrekt linjär anpassning har presenterats för det korrekta intervallet och genom att använda den har rätt svar givits med två till fyra gällande siffrors noggrannhet. (2 p.)
Typiska fel:
Förändringshastigheten för temperaturen har beräknats genom att använda två datapunkter eller hela mätmaterialet.
3.2 Med hur stor effekt överförs värmeenergi till vattnet? Använd dig av resultatet från deluppgift 3.1 vid beräkningen. 4 p.
Tabelluppgifter:
Vattnets specifika värmekapacitet c_V=4,19\,\text{kJ/(kg}\,\text{K}
Vattnets volym V =0,20 L
Vattnets massa m_v=1,00\,\text{kg/L}\cdot 0,020\,\text{L}=0,20\,\text{kg}
Till vattnet överförs energi med effekten
P_v =Q /(~D t) =c_v m_v (~D T) /(~D t) =c_v m_v *(~D T) /(~D t)
P_v =4,19 kJ /(kg K) *0,20 kg *0,02567 K/s =0,02151146 kJ/s ~~22 W
Poängsättning:
En korrekt storhetsekvation för effekten har presenterats med hjälp av vattnets massa och temperaturens förändringshastighet (2 p.)
Ett korrekt värde för effekten som beräknats med hjälp av anpassningen har med två eller tre gällande siffrors noggrannhet givits inom intervallet 21 W - 22 W (2 p.)
Typiska fel:
Effekten har bestämts genom att använda värden för temperaturen vid tidpunkterna i början och slutet.
3.3 Med hur stor verkningsgrad värmer anordningen upp vattnet? 4 p.
Från videon:
Glödlampans spänning U =12,00 V
Glödlampans elektriska ström I=2,14\,\rm{A}
Den elektriska effekten P_s=UI=12,00\,\text{V}\cdot 2,14\,\text{A}=25,68\,\text{W}
Verkningsgraden, då den inmatade effekten är den elektriska effekten och nyttoeffekten är vattnets uppvärmningseffekt: \eta = \frac{P_\text{v}}{P_{\rm e}} = {\rm (21,51146}\,{\rm W)/(25,68}\,{\rm W)} = {\rm 0,83767368} \approx {\rm 84}\,\%
Poängsättning:
Den elektriska effektens storhetsekvation har givits och de korrekta värdena för spänningen och den elektriska strömmen har satts in i den. Alternativt duger även den elektriska effektens storhetsekvation samt rätt värde på effekten. (2 p.)
Ett korrekt värde för verkningsgraden har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,80 - 0,85 (2 p.)
Typiska fel:
Carnotverkningsgraden har beräknats.
3.4 På grund av vilka orsaker är verkningsgraden inte 100 %? Ge tre orsaker. Du kan anta att mätningsfelen inte är betydande. 3 p.
Som vattenuppvärmare är anordningens verkningsgrad mindre än 100 %, eftersom
-
förutom vattnet värmer anordningen dessutom kärlet, lampan och dess fäste
-
trots värmeisoleringen överförs värmeenergi från anordningen genom ledning i locket och metalledningarna
-
en del av den elektriska energin omvandlas via inre energi till strålningsenergi, och den termiska strålningen, inkluderande synligt ljus, som anordningen avger för med sig energi.
-
på grund av ohmiska effektförluster har en del av den elektriska energin omvandlats till värmeenergi i elledningarna.
Poängsättning:
Tre korrekta orsaker har presenterats. (Varje korrekt orsak ger 1 poäng, totalt 3 poäng.)
Ifall fler än tre orsaker har presenterats bedöms de tre sämsta av dem.
Typiska fel:
Det har berättats att energin flyr, försvinner, eller förloras, utan att berätta att det överförs från systemet till dess omgivning.
Dålig värmeisolering har presenterats som orsak utan att nämna att energin överförs till omgivningen.
Mätinstrumentens fel har presenterats som orsak.
4. En heliumballong 15 p.
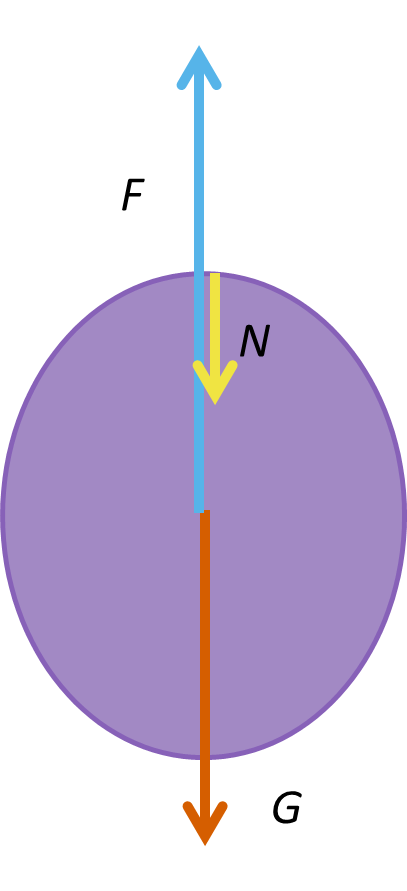
4.1 En heliumfylld ballong är stationär i taket i ett rum. Rita ballongens kraftfigur. Du kan använda dig av bild som en del av ditt svar. 5 p.
Poängsättning:
En korrekt ritad kraftfigur där krafterna tyngd (G), stödkraft (N) och lyftkraft (F) är namngivna och betecknade med symboler. (5 p.)
Följande poängavdrag görs från kraftfiguren:
-
För grova fel (saknade krafter, överlopps krafter eller krafter som verkar i fel riktning) är avdraget fem poäng.
-
För betydande fel (krafternas summa avviker från noll, angreppspunkterna för en eller flera av krafterna är fel, flera av krafterna har samma symbol eller namn, en eller fler av krafternas namn saknas) är avdraget två poäng per typ av fel.
-
Ifall en hastighets- eller accelerationsvektor är ritad fast i ballongen är avdraget fem poäng.
-
Ifall luftmotstånd är ritad i figuren eller namngiven är avdraget fem poäng.
4.2 Med hur stor kraft påverkar taket ballongen när ballongen är stationär i taket i rummet? 6 p.
Enligt Newtons II lag är
\Sigma \vec{F} = m\vec{a}
\vec{G}+\vec{N}+\vec{F}=m\vec{a}
Accelerationen är noll, alltså är
N-F+G=0
N=\rho_lVg-mg
=\rho_lVg-(m_b+\rho_{He}V)g
=1,29 kg/m^3 *0,0053 m^3 *9,81 m/s^2 -(0,0038 kg +0,178 kg/m^3 *0,0053 m^3) *9,81 m/s^2 =0,02054 N
Storleken på den nedåtriktade stödkraften är 21\,\rm{mN}.
Poängsättning:
Lösningen har motiverats genom att nämna att ballongen är i jämvikt. Alternativt har Newtons II lag nämnts samtidigt som det berättats att ballongens acceleration är noll / att ballong är stationär. (2 p.)
En korrekt storhetsekvation för krafternas jämvikt i y-riktningen har presenterats. (2 p.)
Ett korrekt värde för stödkraften har med två eller tre gällande siffrors noggrannhet givits inom intervallet 20 mN - 21 mN. (2 p.)
Typiska fel:
-
Massan för heliumgasen har inte beaktats i lösningen.
-
Takets stödkraft saknas i lösningen.
4.3 Ballongen dras ner till golvnivå. Efter det släpps ballongen, varvid den stiger tillbaka upp till taket i rummet. Graf visar ballongens hastighet som funktion av tiden efter att ballongen släppts. Hur stort luftmotstånd påverkar ballongen precis innan den träffar taket? 4 p.
Ur grafen ser vi att ballongen rör sig med en konstant hastighet innan den träffar taket. Då är krafternas summa noll, och utgående från krafternas jämvikt måste luftmotståndet vara lika stort som stödkraften beräknad i deluppgift 4.2, alltså 21 mN. Kraften riktar sig i motsatt riktning till ballongens rörelse, alltså nedåt.
Poängsättning:
Med hänvisning till bilden har det berättats att ballongs rörelse är likformig. (2 p.)
Det har berättats att luftmotståndet är lika stort som stödkraften i deluppgift 4.2 eller ett korrekt värde för storleken på luftmotståndet har med två eller tre gällande siffrors noggrannhet givits inom intervallet 20 mN - 21 mN (2 p.)
5. En lyftkran 15 p.
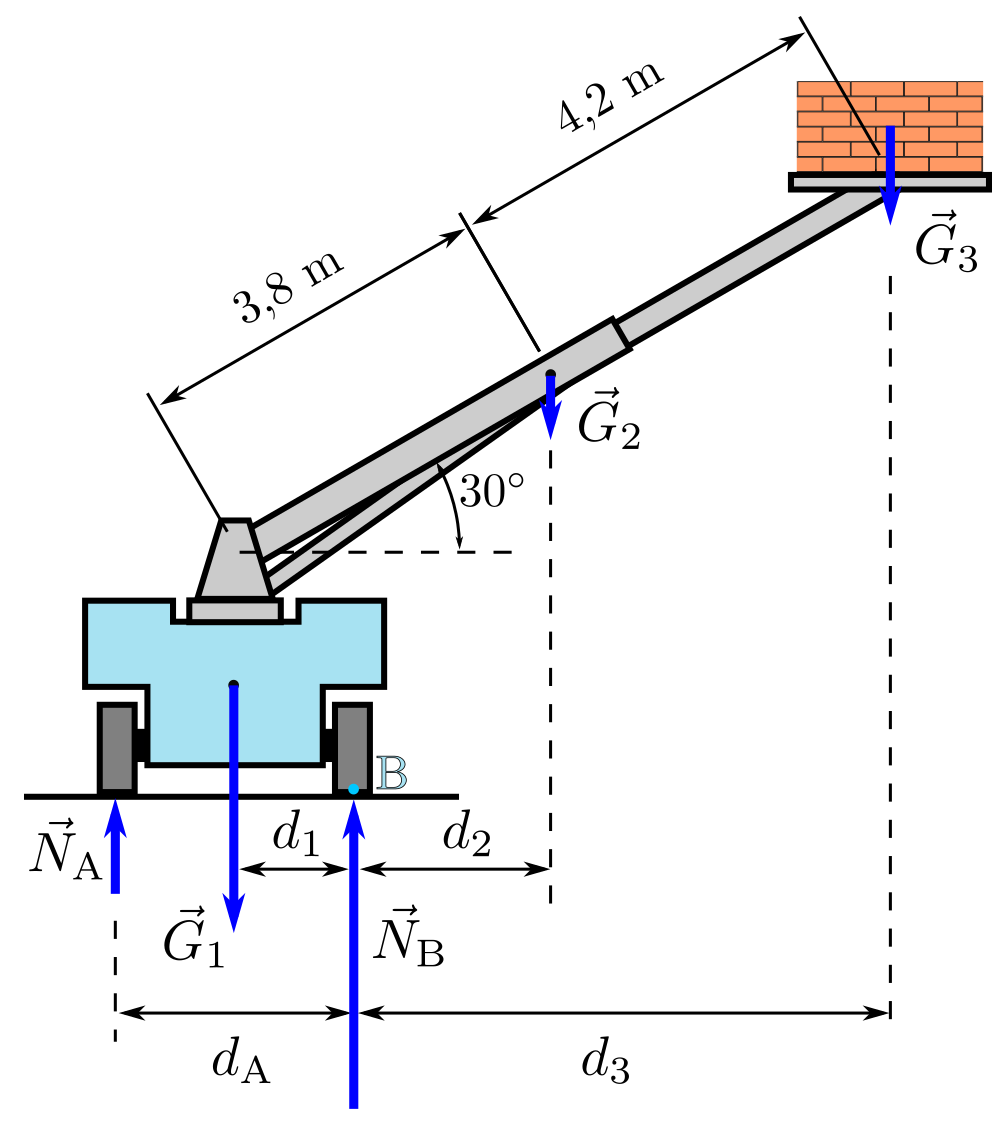
5.1 Med hur stora krafter belastar larvfötterna A och B jorden? Du kan använda dig av bild då du ritar kraftfiguren. 11 p.
På kombinationen av lyftkransbilen, bommen och tegellasset verkar enligt bilden tyngdkrafterna \vec{G}_1, \vec{G}_2 och \vec{G}_3 och stödkrafterna \vec{N}_{\rm A} och \vec{N}_{\rm B}. Tyngdaccelerationen är g=9,81\,\frac{\rm m}{{\rm s}^2}. Massorna för de olika delarna i kombinationen är m_1=3200\,{\rm kg}, m_2=220\,{\rm kg} och m_3=320\,{\rm kg} och tyngdkrafterna är därmed G_1=m_1g=31,39\,{\rm kN}, G_2=m_2g=2,158\,{\rm kN} och G_3=m_3g=3,139\,{\rm kN}. För krafterna väljer vi den positiva riktningen uppåt. Systemet är i jämvikt, alltså får vi enligt Newtons II lag krafternas jämviktsvillkor i formen
N_{\rm A}+N_{\rm B}-G_1-G_2-G_3=0.
Vi skriver kraftmomentens jämviktsvillkor i förhållande till axeln B som är markerad i bilden. Vi väljer kraftmomentens positiva riktning som medurs. Krafternas momentarmar är
d_1=1,4\,{\rm m}
d_2=(3,8\,{\rm m})\cos 30^{\circ}-d_1=1,891\,{\rm m}
d_3=d_2+(4,2\,{\rm m})\cos 30^{\circ}=5,528\,{\rm m}
d_{\rm A}=2d_1=2,8\,{\rm m}.
Ur kraftmomentens jämviktsvillkor får vi
\Sigma M_{\rm B}=N_{\rm A}d_{\rm A}-G_1d_1+G_2d_2+G_3d_3=0
och vidare får vi stödkraften som verkar på larvfot A
N_A=\frac{G_1d_1-G_2d_2-G_3d_3}{d_A}=8,040\,\rm{kN}\approx 8,0\,\rm{kN}
och ur krafternas jämviktsvillkor får vi stödkraften som verkar på larvfot B
N_{\rm B}=G_1+G_2+G_3-N_{\rm A}=28,65\,{\rm kN}\approx 29\,{\rm kN}.
Enligt Newtons III lag påverkar larvfot A jorden med kraften 8,0 kN och larvfot B påverkar jorden med kraften 29\,\rm{kN}.
Poängsättning:
Det har givits en korrekt ritad kraftfigur där krafterna är namngivna. (3 p.)
För kraftfiguren görs följande avdrag:
-
Om kraftfiguren har en kraft som är felaktig, saknas, eller verkar i fel riktning är avdraget tre poäng.
-
Om de inbördes längderna på stödkrafterna eller de inbördes längderna på tyngderna är felaktiga är avdraget en poäng.
-
Om en eller flera av krafterna har fel angreppspunkt är avdraget en poäng.
-
Om namnet eller symbolen för en eller flera av krafterna saknas är avdraget en poäng.
-
Om samma symbol används för flera krafter är avdraget en poäng.
Lösningen är motiverad genom att nämna systemets jämvikt eller Newtons II lag. (1 p.)
En korrekt storhetsekvation för kraftmomentens jämvikt har presenterats i skalärform. Ur lösningen framgår vilken vridningspunkt som använts. (2 p.)
En korrekt storhetsekvation för krafternas jämvikt har presenterats i skalärform, eller alternativt har en annan korrekt storhetsekvation för kraftmomentens jämvikt presenterats i skalärform. (2 p.)
Storlekarna för krafterna som påverkar jorden har korrekt motiverats genom tanken om en kraft-motkraft eller så har Newtons III lag nämnts. (1 p.)
Korrekt värde har med två eller tre gällande siffrors noggrannhet givits för kraften N_A (1 p.) och för kraften N_B (1 p.)
5.2 Om bommen förlängs för mycket kommer lyftkranen att välta. Varför? Vilka delar kan läggas till lyftkranen för att förhindra att den välter? Ett ändringsförslag räcker. 4 p.
En förlängning av bommen ökar på storleken av momentarmarna d_2 och d_3 för \vec{G}_2 och \vec{G}_3 och ytterligare på kraftmomenten för de här krafterna. Om de här ”fällande” kraftmomentens summa blir större än det utjämnande, konstanta kraftmomentet från \vec{G}_1 så välter bilen. Det här kan undvikas genom att installera stödfötter som sträcker sig tillräckligt långt ut på lastens sida av bilen eller genom att placera en motvikt på bilens andra sida.
Poängsättning:
Det har berättats att en förlängning av momentarmen ökar storleken på de vältande krafternas kraftmoment eller förskjuter systemets massmedelpunkt utanför stödytan. (2 p.)
Som förbättringsförslag har givits antingen stödfötter som fästs i bilen eller en montering av extra vikter på bilen. (2 p.)
Ifall fler än ett förbättringsförslag har givits som svar bedöms det sämre svaret.
Typiska fel:
En stödfot som fästs antingen i bommen eller i lasten har givits som förbättringsförslag.
6. Strömmätare 15 p.
6.1 Du vill mäta den elektriska strömmen genom ett motstånd i en strömkrets. Hur ska en strömmätare kopplas till strömkretsen? Motivera ditt svar med hjälp av Kirchhoffs strömlag. 4 p.
En strömmätare kopplas i serie med motståndet.
Enligt Kirchhoffs strömlag delar sig en elektrisk ström i de olika grenarna av en strömkrets så att summan av de elektriska strömmarna som kommer till en punkt i kretsen är lika stor som summan av de elektriska strömmarna som går ut från punkten.
Om strömmätaren kopplas på fel sätt, parallellt med motståndet, delar sig den elektriska strömmen mellan strömmätaren och motståndet, och strömmätaren mäter endast den del av den totala elektriska strömmen som inte går genom motståndet.
Då strömmätaren kopplas på rätt sätt, i serie med motståndet, delar sig den elektriska strömmen inte mellan strömmätaren och motståndet, varvid en lika stor elektrisk ström går genom både mätaren och motståndet.
Poängsättning:
Det har berättats eller grafiskt presenterats korrekt att strömmätaren kopplas i serie med motståndet. (2 p.)
Det har berättats utgående från Kirchhoffs strömlag att den elektriska strömmen delar sig i en förgreningspunkt i strömkretsen, och med hjälp av det har det motiverats att det ur detta följer att det är lika stora elektriska strömmar i motståndet och strömmätaren i en seriekoppling. (2 p.)
Ifall något annat kopplingssätt än seriekoppling har givits som svar ges noll poäng för deluppgiften.
Typiska fel:
Det har påståtts att strömmätaren ska kopplas parallellt med motståndet.
6.2 Med hjälp av strömkretsen i bild kan man bestämma den inre resistansen, R_{\rm m}, hos en verklig strömmätare. Förmotståndet R_0 i kretsen har en resistans som är mycket större än det reglerbara motståndets resistans R_{\rm x}, alltså är R_0\gg R_{\rm x}. Därför hålls den totala elektriska strömmen, I_0, konstant oberoende av det reglerbara motståndets inställningar. Härled ett uttryck för strömmen genom strömmätaren med hjälp av I_0, R_{\rm x} och R_{\rm m}. 7 p.
Resistansen, R_0, hos förmotståndet i kretsen är mycket större än det reglerbara motståndets resistans, varvid förmotståndet avgör storleken på den totala elektriska strömmen I_0 i kretsen. Därmed kan vi med hjälp av Kirchhoffs lagar undersöka hur den totala elektriska strömmen delar sig mellan det reglerbara motståndet och mätaren som är parallellkopplade.
Den totala elektriska strömmen: I_0=I_{R_{\rm x}}+I, där I_{R_{\rm x}} är den elektriska strömmen som går genom det reglerbara motståndet och I är den elektriska strömmen som går genom strömmätaren.
Förändringarna i potentialen över det reglerbara motståndet och mätaren: U_{R_{\rm x}}=U_{\rm m}, alltså är R_{\rm x}I_{R_{\rm x}}=R_{\rm m}I där R_{\rm x} är det reglerbara motståndets resistans och R_{\rm m} är mätarens inre resistans.
Genom att kombinera de här ekvationerna får vi R_{\rm x}(I_0-I)=R_{\rm m}I, ur vilket vi kan lösa för den elektriska strömmen som går genom mätaren I=I_0\bigl(\frac{R_{\rm x}}{R_{\rm x}+R_{\rm m}}\bigr).
Poängsättning:
En korrekt storhetsekvation för de elektriska strömmarna i kretsens förgreningspunkt har givits i enlighet med Kirchhoffs strömlag. (2 p.)
En korrekt storhetsekvation i enlighet med Kirchhoffs spänningslag har givits eller så har det på ett korrekt sätt presenterats att spänningarna över det reglerbara motståndet och strömmätaren är lika stora. (2 p.)
Den korrekta storhetsekvationen för den elektriska strömmen genom mätaren har givits. (3 p.)
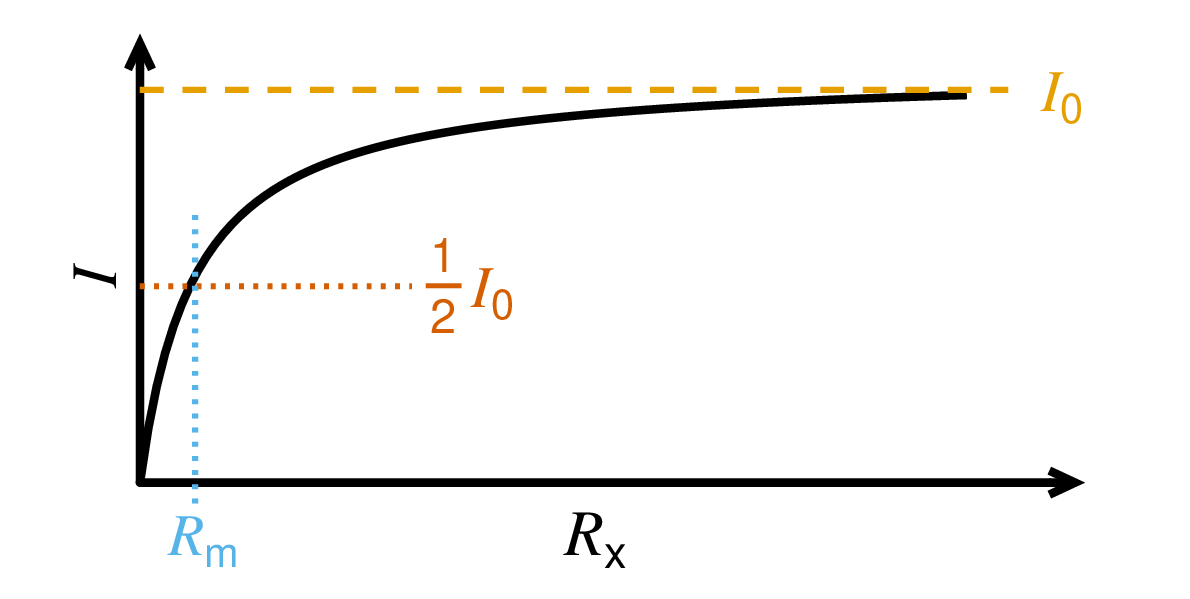
6.3 I graf har värdet på den elektriska strömmen som strömmätaren i kretsen i bild visar ritats upp som funktion av det reglerbara motståndets resistans. Spänningen från likspänningskällan och resistansen för förmotståndet i kretsen är okända. Hur kan du bestämma den inre resistansen hos strömmätaren med hjälp av grafen? Gör dessutom en markering i graf som visar från vilken punkt den inre resistansen hos strömmätaren kan avläsas och bifoga den grafen till ditt svar. 4 p.
Då resistansen hos det reglerbara motståndet som är parallellkopplat med mätaren är satt så lågt som möjligt kommer merparten av den elektriska strömmen att gå genom det reglerbara motståndet. Värdet som mätaren visar är då nära noll.
Om resistansen hos det reglerbara motståndet är satt så högt som möjligt kommer merparten av den elektriska strömmen att gå genom mätaren. Värdet som mätaren visar är då nära värdet för den totala elektriska strömmen, I0.
Därför får vi en graf som den i materialet.
Exempelvis: En lika stor elektrisk ström går genom båda komponenterna då det reglerbara motståndets resistans är satt till ett värde som är lika stort som strömmätarens inre resistans. Strömmätarens inre resistans, Rm, kan därmed avläsas från värdet på det reglerbara motståndets resistans vid punkten där värdet som strömmätaren ger är hälften av den totala elektriska strömmen:
Från föregående deluppgift kan man även notera att I=\tfrac{1}{2}I_0, då R_{\rm x}=R_{\rm m}.
Poängsättning:
Det har förevisats att någon bråkdel av den totala elektriska strömmen används och att det reglerbara motståndets värde avläses från den punkten. (2 p.)
Med hjälp av bilden har det visats var motståndets värde avläses. (2 p.)
Ifall något annat värde för den elektriska strömmen än hälften av den totala strömmen har valts i grafen ska en storhetsekvation för strömmätarens resistans förevisas. I annat fall är avdraget två poäng.
Typiska fel:
Man har försökt bestämma resistansen för strömmätaren genom att använda grafens riktningskoefficient eller endast den totala strömmen.
7. Ljus 15 p.
7.1 Välj rätt svarsalternativ. 2 p.
- mindre än (2 p.)
7.2 Välj rätt svarsalternativ. 2 p.
- lika stor som (2 p.)
I deluppgifterna 7.3–7.7 godkänns ord med stavfel om det entydigt framgår vad som menas med ordet. Oetablerade termer som är variationer av etablerade termer eller som orsakar fysikaliskt falska intryck godkänns inte.
7.3 Fullborda meningen genom att skriva ett ord i det tomma fältet. 2 p.
- våglängd (2 p.)
Ordet bör syfta på storheten våglängd.
7.4 Fullborda meningen genom att skriva ett ord i det tomma fältet. 2 p.
- reflektion (2 p.)
Ordet bör beskriva fenomenet som kallas reflektion.
7.5 Fullborda meningen genom att skriva ett ord i det tomma fältet. 2 p.
- brytning (2 p.)
Ordet bör beskriva fenomenet brytning.
7.6 Fullborda meningen genom att skriva ett ord i det tomma fältet. 2 p.
- brytningsindex (2 p.)
Ordet bör syfta på storheten brytningsindex eller brytningsförhållande eller en egenskap som beskriver brytningsförmåga.
7.7 Fullborda meningen genom att skriva ett ord i det tomma fältet. 3 p.
- böjningsvinkeln (3 p.)
Ordet bör syfta på storleken av riktningsförändringen orsakad av böjning eller diffraktion, eller på en storhet som beskriver det, liksom vinkeln. Även syftningar på diffraktions- eller böjningsfenomenet godkänns.
8. Alfasönderfall 15 p.
8.1 Skriv ut reaktionslikheten för alfasönderfallet av Rn-222. 3 p.
_86^222Rn -> _84^218Po +_2^4He
Poängsättning:
Korrekt reaktionslikhet för sönderfallet har givits. (3 p.)
För alfapartikeln kan även beteckningen ~a användas.
8.2 Varför orsakar radongas en betydande stråldos, trots att alfastrålningen som den utsänder stoppas redan av exempelvis ett pappersark? 4 p.
Radon är en ädelgas som kommer in i lungorna tillsammans med inandningsluften. I lungornas vävnad finns det inte ett cellager som skyddar från strålning, så som det finns på huden, alltså överlåter alfastrålningen sin energi direkt till den levande vävnaden och orsakar strålningsskador i den.
Poängsättning:
Det har berättats att radongas transporteras till lungorna med inandningsluften. (2 p.)
Det har berättats att alfapartiklarna överlåter sin energi till lungvävnaden eller joniserar lungvävnaden. (2 p.)
Typiska fel:
-
Det har tänkts att stråldosen storlek orsakas av halveringstiden för radon.
-
Det har tänkts att alfapartiklarna transporteras till lungorna med inandningsluften.
8.3 Beräkna med hjälp av tabell den frigjorda energin vid alfasönderfallet av Rn-222. Vilken typ av energi visar sig den frigjorda energin som genast efter sönderfallet? 8 p.
Massdefekten \Delta m vid alfasönderfall beräknas som skillnaden mellan utgångs- och slutprodukternas massa. Eftersom slutprodukternas massa är mindre är massan för Rn-222 så ger processen upphov till en massdefekt, alltså frigörs energi: Q=\Delta m c^2
Ur ekvationen \Delta m=m_{\rm Rn}-(m_{\rm Po}+m_{\rm He}) får vi \Delta m= 222,017576 \mathrm{u} - 218,008971\mathrm{u}-4,002603\mathrm{u}\approx 0,006002\,{\rm u}\approx 9,967\cdot 10^{-30}\,{\rm kg}. Vid den här beräkningen är det viktigt att använda massan för He-4-atomen, eftersom elektronerna bevaras vid reaktionen. Om massan för en alfapartikel används bör massan för två elektroner läggas till uttrycket inom parentes.
Genom att multiplicera \Delta m med kvadraten av ljusets hastighet får vi Q=\Delta mc^{2}\approx 8,957\cdot 10^{-13}\,{\rm J}=5,591\,{\rm MeV}. Det är vettigt att avrunda resultatet till värdet 5,59\,{\rm MeV}, trots att de numeriska värdena har många gällande siffror, därför att massdefektens formel innehåller differensen av värden som ligger nära varandra.
Energin Q som frigörs vid alfasönderfallet delas på alfapartikelns och dotterkärnans rörelseenergier.
Poängsättning:
Massdefektens storhetsekvation har presenterats med hjälp av massorna för radon, polonium och alfapartikeln, eller rätt siffervärde för massdefekten har givits. (3 p.)
Korrekt värde för den frigjorda energin har med två till fem gällande siffrors noggrannhet givits inom intervallet 5,550 MeV - 5,620 MeV (3 p.)
Ifall det i beräkningarna av massdefekten och den frigjorda energin felaktigt har använts massan för helium istället för massan för alfapartikeln är avdraget tre poäng.
Det har svarats att den frigjorda energin visar sig som sönderfallsprodukternas rörelseenergi (2 p.)
Ifall någon annan form av energi har nämnts utöver sönderfallsprodukternas rörelseenergi ges inga poäng för identifiering av energiformen.
Typiska fel:
-
Istället för heliums massa har alfapartikelns massa använts för att bestämma massdefekten.
-
Det har påståtts att den frigjorda energin visar sig som strålningsenergi.
Del 3: 20-poängsuppgifter
9. En gascylinder 20 p.
Volymen, trycket och temperaturen för gasen i cylindern mäts med en dator.
I utgångsläget finns det luft i cylindern med samma tryck och temperatur som den yttre luften. Mätningen påbörjas och kolven trycks ner snabbt. Kolven hålls på plats en stund och får sedan studsa upp igen. Kolven förblir sedan i sitt övre läge. Graferna för volymen, trycket och temperaturen som presenteras i bild erhölls i mätningen.
Vi undersöker trycket, temperaturen och den inre energin för luften i cylindern vid experimentets olika skeden. Du kan anta att luft beter sig som en ideal gas i experimentet.
9.1 Skede 1: Kolven trycks ner snabbt. 6 p.
9.1.1 Hur beter sig luftens tryck vid mätningarna i skede 1? Förklara varför trycket beter sig på det observerade sättet utgående från mätresultaten för de övriga storheterna och med hjälp av en för situationen lämplig gaslag. 3 p.
Ökningen i trycket kan förklaras med tillståndsekvationen för en ideal gas \frac{pV}{T}={\rm konstant}\,\Rightarrow\, p={\rm konstant}\cdot\frac{T}{V}
Temperaturen ökar och volymen minskar, alltså ökar trycket.
Poängsättning:
Det har svarats att trycket ökar. (1 p.)
Förklaringen har motiverats genom att nämna tillståndsekvationen för en ideal gas. (1 p.)
Ökningen av trycket har med hjälp av tillståndsekvationen för en ideal gas motiverats genom en minskning i volymen och en ökning i temperaturen. (1 p.)
Typiska fel:
En ökning i trycket har endast motiverats med en minskning i volymen.
9.1.2 Förklara med hjälp av en av termodynamikens huvudsatser som är lämplig för situationen, hur luftens inre energi beter sig i skede 1. 3 p.
Situationen beskrivs av termodynamikens första huvudsats \Delta U=Q+W: förändringen i den inre energin hos luften är lika stor som summan av värmeenergin som överförs mellan luften och omgivningen och arbetet som kraften utför på luften. Kraften som kolven påverkar luften med utför ett positivt arbete. Förändringen i volymen sker snabbt, alltså hinner värmeenergi inte överföras från luften under kompressionen. Därmed är Q\approx 0. Den inre energin hos luften ökar med ett belopp som motsvarar det utförda arbetet, \Delta U=W>0. Det här uttrycker sig som en temperaturökning hos luften, eftersom den inre energin hos en ideal gas är proportionell mot temperaturen.
Poängsättning:
Det har berättats att ett arbete utförs på gasen. (1 p.)
Det har berättats att inget värme överförs från gasen. (1 p.)
Termodynamikens första huvudsats har nämnts och med hjälp av den har det korrekt motiverats att gasens inre energi ökar då ett arbete utförs på gasen och inget värme överförs från gasen. (1 p.)
Typiska fel:
Förändringen i gasens inre energi har endast motiverats med hjälp av arbetet som utförs på gasen.
9.2 Skede 2: Kolven hålls på plats i det nedre läget. 6 p.
9.2.1 Hur beter sig luftens temperatur vid mätningarna i skede 2? Varför beter sig temperaturen på det observerade sättet? 3 p.
Temperaturen minskar.
Minskningen i temperaturen beror på det termodynamiska systemets eftersträvan att uppnå termisk jämvikt (termodynamikens nollte huvudsats). Värme överförs från den heta luften till omgivningen, eftersom luften är i kontakt med cylinderns väggar som är vid rumstemperatur. Då kyls luften ner. Situationen varar tillräckligt länge för att luften ska hinna svalna till rumstemperaturen.
Poängsättning:
Det har svarats att temperaturen minskar. (1 p.)
Det har berättats att systemet eftersöker en termisk jämvikt med omgivningen. (2 p.)
9.2.2 Förklara med hjälp av en av termodynamikens huvudsatser som är lämplig för situationen, hur den inre energin för luften i cylindern beter sig i skede 2. 3 p.
Kolven rör sig inte, alltså utför kraften som påverkar luften inte något arbete: W=0. Luften kyls ner, alltså avger den värmeenergi. Enligt termodynamikens första huvudsats är \Delta U =Q < 0 och luftens inre energi minskar.
Poängsättning:
Det har berättats att gasen inte utför arbete. (1 p.)
Det har berättats att gasen avger värme. (1 p.)
Termodynamikens första huvudsats har nämnts och med hjälp av den har det korrekt motiverats att gasens inre energi minskar då gasen inte utför ett arbete och värme överförs från gasen. (1 p.)
Ifall värmet som avges från gasen har behandlats som en tillståndsvariabel kan endast ett poäng för en korrekt behandling av arbetet som gasen utför erhållas för deluppgiften.
Typiska fel:
Förändringen i gasens inre energi har endast motiverats med hjälp av värmet som avges från gasen.
9.3 Skede 3: Kolven får studsa upp igen. 5 p.
9.3.1 Förklara med hjälp av en av termodynamikens huvudsatser som är lämplig för situationen, hur luftens inre energi beter sig i skede 3. 3 p.
Situationen beskrivs av termodynamikens första huvudsats \Delta U=Q+W. Nu utför kraften som påverkar luften ett negativt arbete, eftersom kraften och förflyttningen är riktade i motsatta riktningar. Återigen är volymförändringen så snabb att värmeenergi inte hinner överföras till luften under expansionen, alltså är Q\approx 0. Luftens inre energi minskar med ett belopp som motsvarar det utförda negativa arbetet, \Delta U =W < 0
Poängsättning:
Det har berättats att gasen utför ett arbete. (1 p.)
Det har berättats att inget värme överförs till gasen. (1 p.)
Termodynamikens första huvudsats har nämnts och med hjälp av den har det korrekt motiverats att gasens inre energi minskar då gasen utför ett arbete och inget värme överförs till gasen. (1 p.)
Typiska fel:
Förändringen i gasens inre energi har endast motiverats med hjälp av arbetet som gasen utför.
9.3.2 Hur beter sig luftens temperatur vid mätningarna i skede 3? Varför beter sig temperaturen på det observerade sättet? 2 p.
Temperaturen minskar.
Den inre energin hos en ideal gas är direkt proportionell mot temperaturen. Luftens temperatur minskar, eftersom den inre energin minskar.
Poängsättning:
Det har svarats att temperaturen minskar. (1 p.)
En minskning i temperaturen har korrekt motiverats med en minskning i gasens inre energi. (1 p.)
9.4 Skede 4: Kolven har återvänt till det övre läget och förblir på plats. 3 p.
9.4.1 Hur beter sig luftens tryck vid mätningarna i skede 4? Förklara tryckets beteende utgående från mätresultaten för de övriga storheterna och med hjälp av en för situationen lämplig gaslag. 3 p.
Trycket ökar.
Ökningen av trycket kan återigen förklaras med lagen p={\rm konstant}\cdot\frac{T}{V}.
Till en början är trycket en aning mindre än det yttre lufttrycket, eftersom volymen har återgått till den ursprungliga och temperaturen är lägre än den yttre luftens temperatur. Då temperaturen ökar till rumstemperaturen och volymen hålls konstant ökar även trycket till värdet det hade i början av mätningen, alltså värdet för det yttre lufttrycket.
Poängsättning:
Det har berättats att trycket ökar eller att trycket återgår till sitt ursprungsvärde. (1 p.)
En förändring i trycket har motiverats genom att nämna tillståndsekvationen för en ideal gas eller Gay-Lussacs lag. (1 p.)
Det har berättats att trycket ökar då temperaturen ökar. Alternativt har tryckets återgång till sitt ursprungsvärde motiverats med att volymen och temperaturen återgår till sina ursprungsvärden. (1 p.)
10. En ylande ljudslang 20 p.
10.1 Betrakta luften inuti slangen. Rör sig luften mot personen som roterar slangen, bort från personen, eller fram och tillbaka i slangen? Motivera ditt svar. 4 p.
Luftstapeln är i princip helt fri att röra sig. Då slangen roteras rör sig luftstapeln enkelt inuti slangen, eftersom stapeln inte är bunden att följa slangens cirkelrörelse. Normalkraften som krävs för att rotera luftstapeln saknas. Det här leder till att luftstapeln inte kan följa med när slangen roteras, utan den rinner ut ur slangen. Luftflödets riktning är alltså bort från handtaget mot den fria ändan av slangen. Luften avlägsnar sig från den fria ändan och ersättande luft kommer in vid handtaget.
Poängsättning:
Det har svarats att luften rör sig bort från personen som roterar slangen (2 p.) och svaret är motiverat korrekt med att normalkraften saknas. (2 p.)
Typiska fel:
Det har svarats att luften rör sig fram och tillbaka i slangen.
10.2 Tre karakteristiska frekvenser har identifierats i spektrum (1) i bild . Bestäm de karakteristiska frekvensernas multipler med hjälp av en lämplig fysikalisk modell. 4 p.
Vi använder modellen för ett rör som är öppet i båda ändarna. För grundtonen ryms en halv våglängd i slangen, för första övertonen ryms en hel våglängd, för andra övertonen ryms 3/2 våglängd, och så vidare. Därmed gäller \lambda_n=2L/n, där L är rörets längd och \lambda_n är våglängden. För grundtonen är n = 1, och så vidare.
Eftersom v=\lambda_n f_n, där v är ljudets hastighet och f_n är frekvensen för motsvarande våglängd \lambda_n, får vi genom att kombinera ekvationerna f_n=nv/(2L).
Genom att lägga in de givna värdena för slangens längd och ljudets hastighet ser vi att de tre starkaste frekvenserna som syns i spektrum (1), 806\,\rm{Hz}, 1608\,\rm{Hz} och 2400\,\rm{Hz}, motsvarar övertonerna där n = 4,01, 8,01 ja 11,95, vilka avrundas till heltalen 4, 8 och 12.
Poängsättning:
Lösningen har motiverats genom att använda modellen för att rör som är öppet i båda ändar. (2 p.)
Som svar för de karakteristiska frekvensernas multipler har heltalen 4, 8 och 12 givits. (2 p.)
Som rätt svar godkänns även de korrekt beräknade överfrekvensernas multipler.
Typiska fel:
Ljudets frekvenser har givits som svar.
10.3 Då slangen roteras snabbare ändras frekvensspektrumet till spektrum (2) i bild . Bestäm de karakteristiska frekvensernas multipler. Beräkna hur mycket slangen har töjts. 4 p.
Den första starka frekvensen som syns i spektrum (2) i bild 10.B är vid 1176\,\rm{Hz}. Utöver den här märker vi övriga övertoner vid 2354 och 3527\,\rm{Hz}. Spektrumet har alltså förskjutits mot högre frekvenser.
Då modellen för ett öppet rör tillämpas på de tre starkaste övertonerna får vi ekvationen f_n=nv/(2L) alltså n=2f_nL/v då vi för övertonerna använder multiplerna n=5,856, då f=1176\,\rm{Hz}, n=11,722, då f=2354\,\rm{Hz}, och n=17,563, då f=3527\,\rm{Hz}.
Vi märker att ekvationen inte producerar heltal lika noggrant som i den tidigare deluppgiften. Det här kan korrigeras genom att öka slangens längd en aning, eftersom längden är direkt proportionell mot övertonens multipel:
L=vn/(2f_n).
De två första frekvenserna är mycket nära heltalen 6 och 12, och skillnaden mellan övertonerna är ungefär 1150\,\rm{Hz}, ur vilket vi kan konstatera att den tredje skulle ha heltalet n=12+6=18. Genom att sätta in de här heltalen och frekvenserna från spektrumet i det tidigare uttrycket får vi
L = 0,875 m (n = 6), L = 0,874256 m (n = 12) och L = 0,875248 m (n = 18). Slangens längd avrundas till medelvärdet 0,875\,\rm{m} och töjningen är därmed \Delta L=(0,875-0,854)\,\text{m}=2,1\,\text{cm}.
Poängsättning:
Som svar för multiplerna har de korrekta heltalen 6, 12 och 18 givits. (2 p.)
Ett korrekt värde för slangens töjning har med två eller tre gällande siffrors noggrannhet givits inom intervallet 1,90 cm - 2,30 cm (2 p.)
10.4 Varför har de karakteristiska frekvenserna i spektrum (2) i bild förskjutits till högre frekvenser? 4 p.
Då slangen roteras snabbt ökar normalaccelerationen för slangens väggar och en ännu större normalkraft skulle krävas för att hålla luften på plats i slangen. Eftersom normalkraften saknas kommer hastigheten på luftflödet inuti slangen att öka ytterligare, och i och med det kommer även frekvenserna för vibrationerna orsakade av vecken att öka, då frekvensen med vilken luftflödet ”kolliderar” med vecken också kommer att öka när flödeshastigheten ökar. Slangen kommer alltså att excitera högre övertoner (lågfrekventa vibrationer förekommer inte längre).
Poängsättning:
Det har berättats att hastigheten för luftflödet i slangen ökar då slangen roteras snabbare. (2 p.)
Det har berättats att luftstapeln kolliderar med vecken oftare då flödeshastigheten är större. (2 p.)
Typiska fel:
Förskjutningen av frekvenserna mot högre värden har motiverats med töjningen av slangen.
10.5 Härled ett uttryck som visar vilken överton som ljuder i slangen då hastigheten för luften som flödar i slangen är u. 4 p.
Vi låter avståndet mellan vecken vara d. Då luftens flödeshastighet inuti slangen är u, kommer luftflödet att kollidera med efterföljande veck med frekvensen f=u/d.
Det förekommer alltså mekaniska vibrationer inuti slangen med frekvensen f. Resonansfrekvenserna för ett öppet rör bestäms å sin sida från ekvationen
f_n=nv/(2L).
Genom att kombinera uttrycken för frekvenserna får vi nv/(2L)=u/d.
Då luftflödets hastighet är u, är multipeln för ljudet från slangen n=2Lu/(vd). Då ljuder alltså övertonenm=n-1=2Lu/(vd)-1 i slangen.
Poängsättning:
Den korrekta storhetsekvationen har givits för frekvensen med vilken luftflödet kolliderar med efterföljande veck. (2 p.)
Den korrekta storhetsekvationen för övertonens multipel har givits. (2 p.)
Som korrekt svar godkänns även en korrekt beräknad och namngiven multipel för den karakteristiska frekvensen.
11. DART-sonden 20 p.
11.1 Beräkna månens banhastighet före kollisionen utgående från dess omloppstid. 8 p.
Radien för en cirkelbana kan lösas med hjälp av banhastigheten v och den ursprungliga omloppstiden T_0 ur ekvationen
v =2 ~p r /T_0 => r =v T_0 /(2 ~p)
Månen (massa M_m) kretsar i en cirkelbana runt asteroiden (massa M_a). Centripetalaccelerationen för månen som rör sig i cirkelbanan orsakas av gravitationskraften, och ur Newtons II lag följer att
\frac{GM_aM_m}{r^2}=\frac{M_mv^2}{r}
Genom att kombinera ekvationerna får vi banhastigheten
v =root3(2 ~p G M_a /T_0) =0,176240 m/s ~~17,6 cm/s
Poängsättning:
Lösningen har motiverats genom att nämna Newtons II lag. (2 p.)
Det har presenterats en rörelseekvation som beskriver månens omlopp, en storhetsekvation för gravitationskraften med hjälp av månens och asteroidens massor, och en storhetsekvation för centripetalaccelerationen med hjälp av omloppstiden, banhastigheten eller vinkelhastigheten. (2 p.)
Det har presenterats en storhetsekvation löst för månens hastighet eller radien för månens omloppsbana. (2 p.)
Månens hastighet har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,17 m/s - 0,18 m/s (2 p.)
11.2 Bestäm förändringen i banhastigheten utgående från förändringen i månens omloppstid. 3 p.
På grund av kollisionen förkortades månens omloppstid till värdet T=11 timmar och 22 minuter, alltså var förändringen i banhastigheten
\Delta v_{\rm observation}=v_{\rm efter}-v_{{\rm f}\ddot{\rm o}{\rm re}}=\sqrt[3]{\frac{2\pi GM_a}{T}}-\sqrt[3]{\frac{2\pi GM_a}{T_0}}=0,0027979\,\frac{\rm m}{\rm s}\approx 2,8\,\frac{\rm mm}{\rm s}.
Poängsättning:
Korrekt värde för förändringen i månens hastighet har givits med två eller tre gällande siffrors noggrannhet. (3 p.)
Typiska fel:
Förändringen i hastigheten har beräknats med antagandet att radien för omloppsbanan hålls oförändrad i kollisionen.
11.3 Beräkna en prognos för förändringen i banhastigheten vid en fullständigt oelastisk kollision. Hur många gånger större är den observerade förändringen i banhastigheten jämfört med prognosen? 6 p.
I bild b) i text 11.A rör sig sonden med en hög hastighet \vec{v}_D i förhållande till månen. Vid en fullständigt oelastisk kollision sjunker sonden bara ner i månen och inget material från månen kastas ut i rymden. Efter kollisionen rör sig både månen och sonden neråt i bildens koordinatsystem med hastigheten \Delta\vec{v} Utgående från lagen om rörelsemängdens bevarande är
m_D v_D (M_k +m_D) ~D v
från vilket vi får förändringen i månens hastighet
\Delta v=\frac{m_D}{M_m+m_D}v_D=0,0008228\,\frac{\rm m}{\rm s}\approx 0,82 \,\frac{\rm mm}{\rm s}.
Förhållandet mellan den observerade förändringen i hastigheten och prognosen för förändringen är
\frac{\Delta v_{\rm observation}}{\Delta v}=\frac{0,0027979\,\frac{\rm m}{\rm s}}{0,0008228\,\frac{\rm m}{\rm s}}\approx 3,4.
Förändringen i månens hastighet var 3,4 gånger så stor som prognosen.
Poängsättning:
Lösningen är motiverad genom att nämna att rörelsemängden bevaras vid kollisionen. (1 p.)
Den korrekta storhetsekvationen för rörelsemängdens bevarande eller en korrekt storhetsekvation löst för hastighetens förändring har presenterats. (2 p.)
Korrekt värde för hastighetens förändring har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,80 mm/s - 0,85 mm/s (2 p.)
Korrekt värde för förhållandet mellan förändringarna i hastigheterna har med två eller tre gällande siffrors noggrannhet givits inom intervallet 3,1 - 3,6 (1 p.)
Typiska fel:
En storhetsekvation för rörelsemängdens bevarande har presenterats, där månens hastighet är hastigheten uppmätt av en extern observatör och sondens hastighet är den relativa hastigheten mellan sonden och månen v_D.
11.4 Vad beror skillnaden mellan prognosen (deluppgift 11.3) och observationen (deluppgift 11.2) på? 3 p.
Då lagen om rörelsemängdens bevarande tillämpas på kollisionsförsöket borde man även ta i beaktande rörelsemängden för det material som slungas ut från månens yta med stor hastighet. Om materialets rörelsemängd är betydande och dess riktning är tillbaka mot sondens infallsriktning, kan månens hastighet förändras mycket mer än vid en fullständigt oelastisk kollision.
Poängsättning:
Det har berättats att även rörelsemängden hos det material som slungas ut i rymden måste beaktas då lagen om rörelsemängdens bevarande används. (3 p.)
Typiska fel:
Skillnaden mellan den observerade förändringen i hastigheten och prognosen är motiverad genom att använda lagen om energins bevarande.