Hyvän vastauksen piirteet: FI – Fysiikka
17.9.2025
Lopulliset hyvän vastauksen piirteet 13.11.2025
Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.
Fysiikan ylioppilaskokeessa arvioinnin kohteita ovat lukion opetussuunnitelman perusteiden mukaisen fysiikan tiedon osaaminen ja soveltamisen taito. Kokeessa arvioidaan myös kokelaan kokeellisen tiedonhankinnan ja -käsittelyn taitoja. Näitä ovat muun muassa kokeensuunnittelu, yleisimpien mittavälineiden käytön hallinta, tulosten esittäminen ja tulkitseminen sekä johtopäätösten tekeminen. Kokeessa arvioidaan niin ikään kokelaan kykyä ymmärtää ja eritellä fysiikan luonteen mukaisia aineistoja. Arvioinnissa kiinnitetään huomiota siihen, että vastauksissa on käytetty fysiikan käsitteitä ja käsiterakenteita asianmukaisesti ja että vastaukset on esitetty selkeästi ja asiasisällön puolesta johdonmukaisesti ja hyvin jäsennellysti.
Hyvä vastaus sisältää vastauksen perustelut, ellei tehtävänannossa ole toisin mainittu. Siitä käy ilmi, että kokelas on tunnistanut oikein fysikaalisen ilmiön ja tarkastelee tilannetta fysikaalisesti mielekkäällä tavalla. Kokelas osaa kuvata sovellettavan fysikaalisen mallin ja perustella, miksi mallia voidaan käyttää kyseisessä tilanteessa. Kun vastaukseen liittyy tilannekuvioita, voimakuvioita, kytkentäkaavioita tai graafisia esityksiä, nämä on tehty selkeästi ja fysiikassa noudatettujen yleisten periaatteiden mukaisesti. Esimerkiksi voimakuviossa voimavektorit on erotettu vektorien komponenteista selkeästi.
Matemaattista käsittelyä vaativan tehtävän hyvässä vastauksessa on suureyhtälöt ja kaavat perusteltu tavalla, joka osoittaa kokelaan hahmottaneen tilanteen fysiikan kannalta oikein. Vastauksessa on esitetty tarvittavat laskut ja muut riittävät perustelut sekä lopputulos. Suureiden arvojen sijoituksia yhtälöön ei tarvitse kirjoittaa näkyviin, jos vastauksessa on selkeästi esitetty, mitä symbolia, lukuarvoa ja yksikköä kullekin suureelle käytetään. Symbolisten laskentaohjelmistojen avulla tehdyt ratkaisut hyväksytään, kunhan ratkaisusta käy ilmi, mihin tilanteeseen ja yhtälöihin ratkaisu symboleineen perustuu ja lopputuloksen yhteydessä on esitetty tehtävänannossa kysytyn suureen suhteen ratkaistu suureyhtälö.
Yleisinä pisteytyksen linjauksina ovat:
- Jos vastauksessa annettujen merkitsevien numeroiden määrä poikkeaa HVP:ssa kirjatusta, vähennetään jokaisen vastauksen kohdalla yksi piste.
- Jos lopputuloksen yksikkö on väärin tai puuttuu, tulos on väärin.
Osa 1: 20 pisteen tehtävä
1. Tehtäviä fysiikan eri osa-alueilta 20 p.
1.1 Kuinka suuri kotikeittiön vedenkeittimen teho on suunnilleen? 2 p.
- 1 000 W (2 p.)
1.2 Kuinka suuri matkapuhelimen latausvirta on suunnilleen? 2 p.
- 1 A (2 p.)
1.3 Kuinka pitkä aika suunnilleen kuluu radioaaltojen kulkemiseen Maasta Kuuhun? 2 p.
- 1 s (2 p.)
1.4 Kuinka suuri hiuksen halkaisija on suunnilleen? 2 p.
- 100 ~mm (2 p.)
1.5 Tuntematon suure X 4 p.
1.5.1 Selvitä yksikkötarkastelun avulla suureen X yksikkö. Kirjoita vastauskenttään vain suureen X yksikkö. 2 p.
- metri (2 p.)
1.5.2 Selvitä yksikkötarkastelun avulla suureen X nimi. Kirjoita vastauskenttään vain suureen X nimi. 2 p.
- matka (2 p.)
- pituus (2 p.)
- välimatka (2 p.)
- etäisyys (2 p.)
1.6 Tuntematon suure Y 4 p.
1.6.1 Selvitä yksikkötarkastelun avulla suureen Y yksikkö. Kirjoita vastauskenttään vain suureen Y yksikkö. 2 p.
- metriä sekunnissa (2 p.)
1.6.2 Selvitä yksikkötarkastelun avulla suureen Y nimi. Kirjoita vastauskenttään vain suureen Y nimi. 2 p.
- nopeus (2 p.)
- vauhti (2 p.)
1.7 Tuntematon suure Z 4 p.
1.7.1 Selvitä yksikkötarkastelun avulla suureen Z yksikkö. Kirjoita vastauskenttään vain suureen Z yksikkö. 2 p.
- sekunti (2 p.)
1.7.2 Selvitä yksikkötarkastelun avulla suureen Z nimi. Kirjoita vastauskenttään vain suureen Z nimi. 2 p.
- aika (2 p.)
Myös muut oikeat ilmaisut hyväksytään.
Osa 2: 15 pisteen tehtävät
2. Kuula putkessa 15 p.
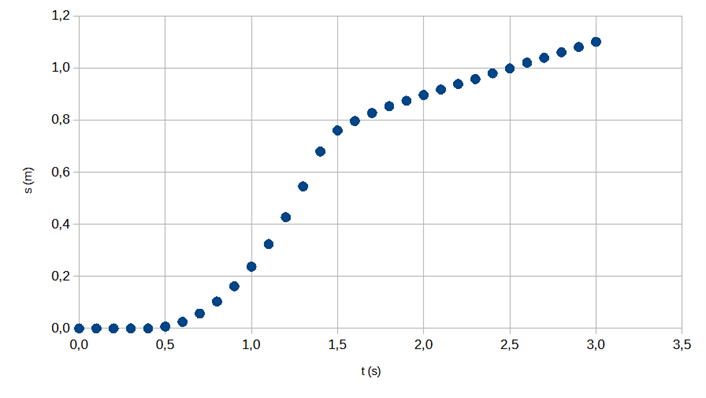
2.1 Laadi taulukkoa käyttäen kuvaaja kuulan kulkemasta matkasta ajan funktiona. Tähän kuvaajaan ei tule graafista tasoitusta. 4 p.
Pisteytys:
On esitetty oikea kuulan kulkeman matkan kuvaaja ajan funktiona. (4 p.)
Kuvaajasta tehdään seuraavat pistevähennykset:
-
Jos on piirretty pylväsdiagrammi, annetaan kuvaajasta nolla pistettä.
-
Jos on piirretty pelkkä murtoviiva, vähennetään kaksi pistettä.
-
Jos datapisteet on yhdistetty murtoviivalla, vähennetään kaksi pistettä.
-
Jos kuvaajaan on piirretty sovite, vähennetään kaksi pistettä.
-
Jos yksi tai useampi datapiste puuttuu kuvaajasta, vähennetään kaksi pistettä.
-
Jos yhden tai molempien akseleiden lukuarvot puuttuvat tai ovat väärin, vähennetään yksi piste.
-
Jos yhden tai molempien akseleiden suureen nimi puuttuu tai ovat väärin, vähennetään yksi piste.
-
Jos yhden tai molempien akseleiden suureen yksikkö puuttuu tai ovat väärin, vähennetään yksi piste.
-
Jos akselit on piirretty väärin päin, vähennetään yksi piste.
Tyypillisiä virheitä:
Kuvaajaan on piirretty pelkkä murtoviiva tai mittauspisteet on yhdistetty murtoviivalla.
Kuvaajaan on piirretty sovite.
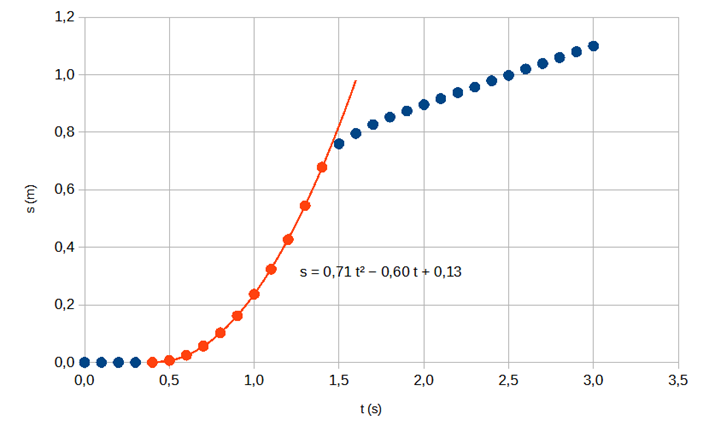
2.2 Selvitä graafisesti piirtämääsi kuvaajaa käyttäen, milloin kuula osuu veden pintaan. Valitse aikaväleistä a–d se, jonka aikana kuula osuu veden pintaan. Perustele valintasi piirtämällä uusi kuvaaja, jossa näkyy osaan mittauspisteistä sovitettu paraabeli. 6 p.
Kuula osuu veden pintaan aikavälillä b.
Perustelu: Kuvaajan s(t) mittauspisteet aikavälillä 0,4–1,4 s osuvat hyvin tarkasti pisteisiin sovitetulle paraabelille. Tämä kertoo, että liike on tällä aikavälillä mittaustarkkuuden rajoissa tasaisesti kiihtyvää. 1,5 sekunnin kohdalla oleva mittauspiste ei osu käyrälle, joten välillä 1,4–1,5 s kiihtyvyys on muuttunut. Tämä johtuu kuulan osumisesta veteen.
(Newtonin II lain mukaan ΣF = ma, joten kiihtyvyyden muutoksen täytyy aiheutua kokonaisvoiman muuttumisesta. Se taas johtuu kuulan osumisesta veteen, sillä vedessä kuulaan alkaa vaikuttaa gravitaation, tukivoiman ja kitkan lisäksi myös huomattava väliaineen vastus.)
Pisteytys:
On annettu oikea kirjain (b) tai aikaväli (1,4 s - 1,5 s) (2 p.)
On esitetty kuvaaja, jossa datapisteisiin on aikavälillä t\le1{,}6~\mathrm{s} oikein sovitettu ylöspäin aukeava paraabeli yhtälöineen (2 p.)
On perusteltu osuman oikea aikaväli datapisteen poikkeamisella paraabelilta, joka on oikein sovitettu mittauspisteisiin välillä 0{,}3~\mathrm{s}\ \le t\le1{,}4~\mathrm{s} (2 p.)
Tyypillisiä virheitä:
Pisteisiin on sovitettu muu funktio kuin paraabeli.
Paraabeli on sovitettu väärälle aikavälille.
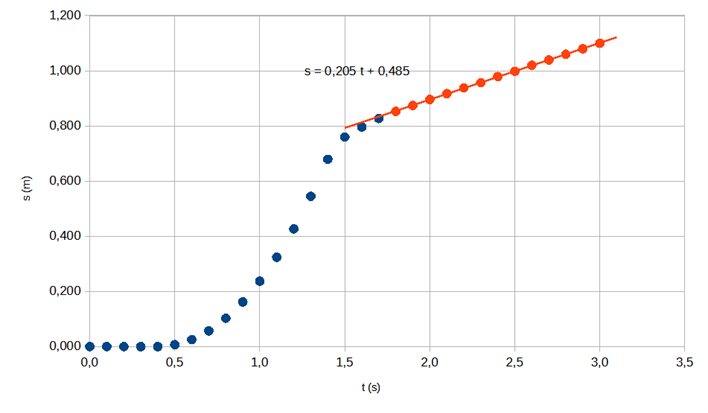
2.3 Määritä kuulan nopeus videolla esiintyvässä tilanteessa, jossa kuula on liikkeellä ja siihen kohdistuvat voimat tasapainottavat toisensa. 5 p.
Kun kuula liikkuu vedessä, kuulaan kohdistuva väliaineen vastus riippuu nopeudesta. Kuulan nopeus asettuu sellaiseksi, että kuulaan vaikuttavat voimat tasapainottavat toisensa. Tällöin kuulan kiihtyvyys on nolla ja nopeus vakio. Tätä tilannetta esittää kuvaajan osuus, jossa datapisteet ovat suoralla.
Kuulan nopeus on suoran kulmakerroin.
Suoran sovituksella saadaan v = 0,205 m/s.
Pisteytys:
On kerrottu että kuulan liike on tasaista, kuulan nopeus on vakio tai kuulan kiihtyvyys on nolla. (1 p.)
Kulmakerroin on määritetty aikavälillä, jonka alaraja on vähintään 1,5 s ja yläraja selvästi suurempi (2 p.)
On annettu oikea nopeuden arvo välillä 0,20 m/s - 0,22 m/s kahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
Tyypillisiä virheitä:
Suora on sovitettu väärälle aikavälille.
3. Maalämpö 15 p.
3.1 Mistä kallioperään varastoitunut lämpöenergia on pääosin peräisin? 3 p.
Lämpöenergia on pääosin peräisin auringosta. Geotermisen energian osuus kasvaa merkittäväksi vasta kilometrien syvyydessä.
Pisteytys:
On kerrottu energian olevan peräisin auringosta (3 p.)
Jos on annettu useampi kuin yksi vastaus, arvostellaan vastauksista huonoin.
Tyypillisiä virheitä:
On väitetty energian olevan peräisin maapallon ytimestä.
Maapallon pinnalla havaitaan lämpötilan vaihtelevan vuodenaikojen mukaan noin 15 metrin syvyyteen asti, eli tässä näkyy Auringon välitön vaikutus. Maapallon pinnalla Auringosta tuleva energiavuo on yli tuhatkertainen maan sisältä tulevaan energiavuohon verrattuna. Sen takia vielä satojen metrien syvyydessä lämpötilan suuruus johtuu ensisijaisesti siitä, että Auringon lämmittävä vaikutus estää lämpötilaa laskemasta Maan säteillessä energiaa avaruuteen.
3.2 Maalämpöjärjestelmän käyttöönotossa kuumavesisäiliöön johdetaan 350 litraa vettä, jonka lämpötila on 7,0 ^@C. Laitteisto kuumentaa veden 2,5 tunnissa 60 ^@C:n lämpötilaan ja kuluttaa tähän 7,4 kWh sähköenergiaa. Määritä järjestelmän lämpökerroin ja laske, millä teholla vesi lämpenee. 7 p.
Veteen siirtynyt lämpömäärä on Q =c m ~DT = c ~r V (T_2 -T_1). Veden tiheys 7 ^@C:n lämpötilassa on ~r =999,90 kg/m^3 Lämpökerroin eli lämpömäärän ja kulutetun sähköenergian suhde on ~ä =~DQ/E =c ~r V(T_2 -T_1)/E =(4,19 kJ/(kg K) *999,90 kg/m^3 *0,35 m^3 *53 K) /7,4 kWh =77,71672755 MJ /(7,4 kW *3600 s) ~~2,9.
Vesi lämpenee teholla P =~DQ/~Dt =77,71672755 MJ /(2,5 *3600 s) =8635,19195 W ~~8,6 kW
Pisteytys:
On annettu veteen siirtyneen lämpömäärän oikea lukuarvo välillä 77,5 MJ - 77,8 MJ (2 p.)
On annettu oikea vastaus lämpökertoimen arvolle välillä 2,90 - 2,92 kahden tai kolmen merkitsevän numeron tarkkuudella. (3 p.)
On annettu tehon oikea arvo välillä 8,62 kW - 8,64 kW kahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
Tyypillisiä virheitä:
On annettu lämmitystehon sijasta sähköteho.
Veteen siirtynyt lämpömäärä on laskettu käyttäen väärää lämpötilan muutosta.
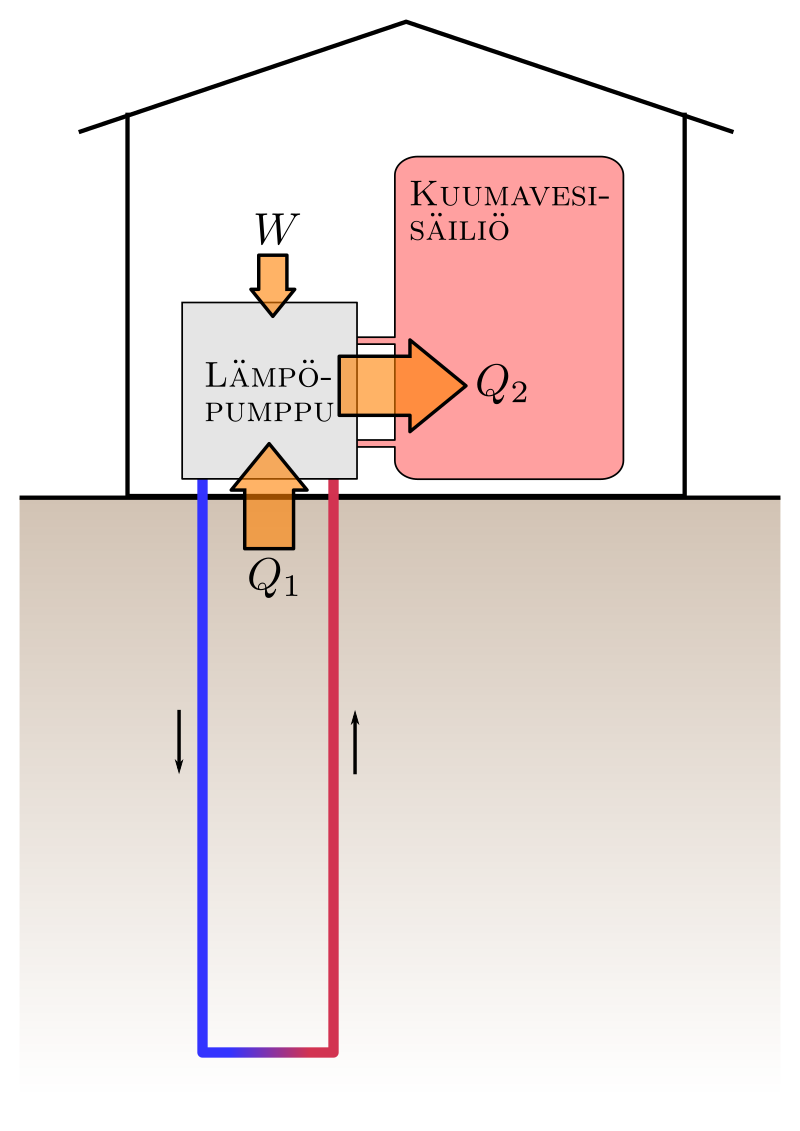
3.3 Piirrä lämpöpumpun energiavirtoja esittävä kaavio ja nimeä siinä esiintyvät suureet. Kirjoita kyseiset suureet toisiinsa yhdistävä yhtälö. Piirtämisessä voit halutessasi hyödyntää kuvaa . 5 p.
Q_1 = maasta siirtynyt lämpömäärä
Q_2 = vesisäiliöön siirtynyt lämpömäärä
W = lämpöpumpun sähköenergialla tekemä työ
Suureille pätee yhtälö Q_1 +W =Q_2
Pisteytys:
On annettu oikea kaavio (3 p.). Oikeassa kaaviossa on esitetty että
-
lämpöä siirtyy maasta pumppuun,
-
lämpöä siirtyy pumpusta vesisäiliöön,
-
työtä tulee pumppuun ulkopuolelta,
ja edellä mainitut kolme suuretta on oikein nimetty.
Kaaviosta annettaan nolla pistettä, jos jokin oikeista suureista puuttuu tai energiaa virtaa väärään suuntaan.
On annettu oikea ja kaavion kanssa ristiriidaton suureyhtälö (2 p.)
Tyypillisiä virheitä:
-
On merkitty siirtyvää energiaa kuvassa esiintyviin mustiin nuoliin.
-
On piirretty lämpöpumppu, jossa on lämpösäiliö ja kylmäsäiliö, mutta jätetty kytkemättä se tehtävän asiayhteyteen.
-
On käsitelty lämpöä tilamuuttajana, esimerkiksi puhumalla kuumavesisäiliön lämmöstä tai nimetty Q2 kuumavesisäiliön energiaksi.
4. Jalkaprässi 15 p.
4.1 Piirrä kelkan ja painojen muodostaman kappaleen voimakuvio, kun kuntoilija pitää kelkkaa ja painoja paikoillaan jalkojensa avulla. Käytä voimakuvion pohjana kuvaa . 3 p.
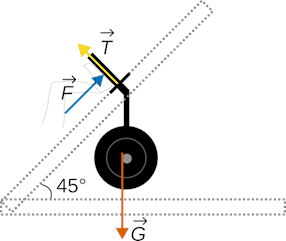 \vec T on tukivoima, \vec G on paino ja \vec F on kuntoilijan kelkkaan kohdistama voima.
Pisteytys:
\vec T on tukivoima, \vec G on paino ja \vec F on kuntoilijan kelkkaan kohdistama voima.
Pisteytys:
Oikein piirretty voimakuvio, jossa tukivoima, paino ja kuntoilijan kelkkaan kohdistama voima nimetty sanallisesti tai symbolilla (3 p.)
Voimakuviosta tehdään seuraavat vähennykset:
-
Vakavasta virheestä (puuttuvat, ylimääräiset tai väärään suuntaan osoittavat voimat) vähennetään kolme pistettä.
-
Merkittävästä virheestä (voiman nimi tai symboli puuttuu, voimien summa eroaa merkittävästi nollasta, useammalla voimalla on sama nimi tai symboli) vähennetään yksi piste per virhetyyppi.
-
Jos voimakuvion pohjana käytetty muuta kuin annettua kuvaa, vähennetään yksi piste.
Tyypillisiä virheitä:
-
Tukivoima on jätetty piirtämättä.
4.2 Kuinka suuri voima kuntoilijan on vähintään kohdistettava kelkkaan, jotta kelkka ja painot pysyisivät ylhäällä paikoillaan? 6 p.
Painot ja kelkka ovat tasapainossa.
Kun kitkaa ei huomioida, voimien tasapaino prässin kiskojen suuntaan on F -G cos(45 ^@) =0.
Painoihin ja kelkkaan vaikuttava painovoima on G =m_(k +p) g, joten kuntoilijan on kohdistettava kelkkaan vähintään voima F =m_(k +p) g cos(45 ^@) =160 kg *9,80665 m/s^2 cos(45 ^@) =1109,495795 N ~~1100 N.
Pisteytys:
On kerrottu että kappale on tasapainossa tai kerrottu että kiihtyvyys on nolla ja perusteltu se oikein Newtonin II lain avulla. (2 p.)
On annettu oikea voimien tasapainoyhtälö kiskojen suunnassa. (2 p.)
On annettu voiman suuruudeen oikea arvo kahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
Tyypillisiä virheitä:
On laskettu kosinin arvo käyttäen väärää kulman yksikköä.
Voimien tasapainoyhtälössä kosinifunktio on nimittäjässä.
4.3 Kuntoilija nostaa kelkan ja painot suoristamalla jalkansa. Aikaa tähän kuluu 2,8 sekuntia. Kuinka suuri on kuntoilijan jalkaprässiin kohdistaman voiman keskimääräinen teho? Jalkojen suoristuksen aikana kelkka liikkuu 55 cm kiskoja pitkin. 6 p.
Yhden jalkojen suoristuksen aikana kelkkaan ja painoihin tehdään työ W =F s =1109,495795 N *55 cm =610,2226872 J.
Kun tämä tehdään 2,8 sekunnin aikana, on keskimääräinen teho P =W/~Dt =610,2226872 J /2,8 s =217,936674 W ~~220 W.
Pisteytys:
On annettu työn oikea suureyhtälö tai lukuarvo. (2 p.)
On annettu tehon oikea suureyhtälö. (2 p.)
On annettu oikea vastaus kahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
5. Aaltoja 15 p.
Tässä tehtävässä on viisi aaltoihin liittyvää osatehtävää. Vastattuasi osatehtävään voit vaihtaa vastausvaihtoehtoa, mutta et voi jättää osatehtävää enää kokonaan ilman vastausta. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, valitse pudotusvalikosta tyhjä rivi ja merkitse osatehtäviin 5.2–5.5 vaihtoehto ”En vastaa”. Oikea vastaus 3 p., väärä vastaus 0 p., ei vastausta 0 p.
5.1 Kahden äänilähteen tuottamat paineen vaihtelut 3 p.
- AC (3 p.)
5.2 Kahden äänilähteen tuottamat aallot 3 p.
- B (3 p.)
5.3 Seinästä heijastuvat aaltopulssit 3 p.
- C (3 p.)
5.4 Ääni ja sen spektri 3 p.
- D (3 p.)
5.5 Metallijousessa etenevä aalto 3 p.
- Aallonpituus on 6 cm. (3 p.)
6. Kondensaattorin energia 15 p.
6.1 Ilmaeristeinen levykondensaattori, jonka kapasitanssi on 0,95 ~mF, on kytkettynä 24 V:n tasajännitelähteeseen. Kondensaattorilevyjen väli täytetään eristelevyllä, jonka materiaalin suhteellinen permittiivisyys on 4,5. Kuinka suuri on kondensaattorin energian muutos, kun eristelevy lisätään? 5 p.
Kondensaattori, jonka kapasitanssi on C =0,95 ~mF, on koko ajan kytkettynä jännitelähteeseen, joten kondensaattorin jännite pysyy vakiona: U =24 V. Kondensaattorin kapasitanssi on suoraan verrannollinen kondensaattorilevyjen välisen eristeen suhteelliseen permittiivisyyteen. Kun ilma (suhteellinen permittiivisyys ~~ 1) korvataan eristeellä, jonka suhteellinen permittiivisyys on ~e_r =4,5, kondensaattorin kapasitanssi kasvaa arvoon ~e_r C.
Kondensaattorin energian muutos on ~DE =E_2 -E_1 =1/2 ~e_r C U^2 1/2 -C U^2 =1/2 (~e_r -1) C U^2 =0,9576 mJ ~~0,96 mJ.
Pisteytys:
On kerrottu, että kondensaattorin jännite pysyy vakiona ja kondensaattorin kapasitanssi muuttuu \varepsilon_r-kertaiseksi. (2 p.)
On annettu oikea energian muutoksen suureyhtälö. (1 p.)
On annettu oikea vastaus välillä 0,956 mJ - 0,958 mJkahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
6.2 Ilmaeristeinen levykondensaattori, jonka kapasitanssi on 1,9 ~mF, kytketään 12 V:n tasajännitelähteeseen. Tämän jälkeen kondensaattori irrotetaan jännitelähteestä. Kondensaattorin levyjä siirretään siten, että niiden välinen etäisyys nelinkertaistuu. Kuinka suuri on kondensaattorin energian muutos, kun levyjä siirretään? 6 p.
Ympäristöstään eristetyn kondensaattorin varaus säilyy.
Alussa kondensaattorin kapasitanssi ja jännite ovat C =1,9 ~mF ja U = 12 V, joten sen varaus on Q =C U =22,8 ~mC Kondensaattorin kapasitanssi on kääntäen verrannollinen levyjen väliseen etäisyyteen, joten etäisyyden nelinkertaistaminen pienentää kapasitanssin arvoon C/4. Kondensaattorin energian muutokseksi saadaan ~DE =E_2 -E_1 =Q^2 /(2 C /4) -Q^2 /(2 C) =3 Q^2 /(2 C) =0,4104 mJ ~~0,41 mJ.
Pisteytys:
On kerrottu, että kondensaattorin varaus säilyy. (2 p.)
On kerrottu, että kondensaattorin kapasitanssi pienenee neljäsosaan. (2 p.)
On annettu oikea vastaus kahden tai kolmen merkitsevän numeron tarkkuudella. (2 p.)
Tyypillisiä virheitä:
On oletettu, että kondensaattorin jännite pysyy vakiona ja saatu vastaukseksi 0,10 mJ.
6.3 Selitä, miksi levyjen siirtäminen osatehtävässä 6.2 muuttaa kondensaattorin energiaa. 4 p.
Kondensaattorilevyt vetävät toisiaan puoleensa sähköstaattisilla voimilla. Levyjen siirtämiseksi etäämmälle toisistaan niihin on siis kohdistettava ulospäin suuntautuvat voimat. Nämä voimat tekevät positiivisen työn, joka varastoituu kondensaattorin sähkökentän energiaksi.
Pisteytys:
Jos vastauksessa on kerrottu, että
-
levyt vetävät toisiaan puoleensa tai
-
ulkoiset voimat tekevät työtä tai
-
energiaa varastoituu sähkökentän energiaksi
annetaan jokaisesta kohdasta kaksi pistettä, yhteensä enintään (4 p.)
Tyypillisiä virheitä:
Yritetään selittää asiaa pelkästään kapasitanssin muutoksella ja mahdollisesti olettaen jännitteen säilyvän vakiona.
7. Liikkuva magneetti 15 p.
7.1 Sauvamagneetin toinen napa on kuvan mukaisesti käännetty kohti oikosuljettua käämiä. Magneetti lähestyy käämiä kuvan esittämällä tavalla. Miksi magneetin liike-energia pienenee, kun se lähestyy käämiä? 4 p.
Liikkuva magneetti indusoi käämiin jännitteen, joka synnyttää virran.
Virtapiirissä kulkevalla virralla on tietty energia, ja tämä energia on peräisin magneetin liike-energiasta. Energian säilyminen edellyttää, että kun käämiin siirtyy energiaa, magneetin liike-energia pienenee.
Pisteytys:
On kytketty vastaus oikein induktioilmiöön. (2 p.)
On kirjoitettu ehjä päättelyketju induktiojännitteestä magneetin liike-energian pienenemiseen. (2 p.)
7.2 Käämissä on N johdinkierrosta, ja sen kokonaisresistanssi on R. Kirjoita lauseke käämin sähkövirran teholle hetkellä, jolloin magneetin nopeus on v. Oleta, että käämin läpäisevän magneettivuon muutosnopeus on suoraan verrannollinen magneetin nopeuteen. Voit merkitä verrannollisuuskerrointa kirjaimella k. Kuinka teho muuttuu käämin resistanssia muutettaessa? 6 p.
Käämiin indusoituu induktiolain mukainen jännite U =-N d ~f /(dt) jossa ~f on magneettivuo käämin läpi. Vuon muutosnopeus on tehtävän mukaan verrannollinen magneetin nopeuteen. Voidaan siis kirjoittaa d ~f /dt ~ v eli d ~f /dt =k v missä k on verrannollisuusvakio.
Tästä seuraa jännitteelle U =-N k v Induktiojännite aiheuttaa virran I, ja Ohmin lain mukaan voimme kirjoittaa U =R I Sähkövirran aiheuttama tehohäviö P =U^2/R =(N k v)^2 /R
Tästä lausekkeesta nähdään, että häviöteho kasvaa, jos resistanssia R pienennetään.
Pisteytys:
On annettu oikea suureyhtälö vuon muutosnopeudelle k:n avulla. (2 p.)
On annettu oikea suureyhtälö teholle k:n avulla. (2 p.)
On kerrottu sanallisesti, että teho kasvaa, kun resistanssi pienenee tai päinvastoin. (2 p.)
7.3 Koe toistetaan, mutta nyt käämi korvataan pitkällä, molemmista päistä avoimella ja johtavasta materiaalista valmistetulla putkella, jonka sisään magneetti asetetaan. Magneetin massa on 52 g, ja sen alkunopeus on 0,30 m/s. Magneetin ja putken välillä ei ole kitkaa, eikä ilmanvastus vaikuta magneettiin. Magneetti ei kuitenkaan ikinä saavuta putken toista päätä. Kuinka paljon energiaa kokeen aikana siirtyy magneetista putkeen? 5 p.
Osatehtävän mukaan magneetti menettää energiaa sen liikkuessa johtavan kappaleen läpi, koska putkeen indusoituu induktiojännitteen aiheuttama pyörrevirta. Magneetin nopeus hidastuu niin tehokkaasti, että se ei pääse putkesta ulos. Tällöin kaikki liike-energia on siirtynyt induktion takia putkeen.
Alussa magneetin kokonaisliike-energia oli 1/2 *m v^2 =1/2 *0,052 kg *(0,30 m/s)^2 =0,00234 J ~~2,3 mJ
Tämän verran energiaa magneetista siirtyy putkeen pyörrevirtojen lämmittäessä putkea.
Pisteytys:
On perusteltu oikein, miten magneetin koko liike-energia siirtyy putkeen. (2 p.)
On annettu oikea suureyhtälö energialle (1 p.) ja sen avulla laskettu oikea vastaus 2-3 merkitsevän numeron tarkkuudella. (2 p.)
Tyypillinen virhe:
On unohdettu korottaa nopeus toiseen potenssiin ja saatu 7,8 mJ.
8. Säteilyn dualismi ja kvantittuminen 15 p.
8.1 Sähkömagneettinen säteily käyttäytyy kuten aaltoliike, eli sähkömagneettisessa säteilyssä esiintyy samanlaisia ilmiöitä kuin muissa aaltoliikkeissä. Anna kaksi esimerkkiä kokeista tai tilanteista, joissa tällaista käyttäytymistä esiintyy. Kerro kummastakin esimerkistä, miten säteilyn käyttäytyminen selittää havaitun ilmiön tai ilmiöt. 6 p.
Esimerkiksi sopivat kokeet, joissa havaitaan sähkömagneettiselle aaltoliikkeelle tyypillisiä ilmiöitä, kuten superpositio eli summautuminen, polarisaatio tai taittuminen rajapinnassa. Ilmiön tulee olla sellainen, jota ei havaita hiukkasilla.
Esimerkkejä kokeista:
-
Valon diffraktio kaksoisraossa tai hilassa: eri raoista kulkenut valo muodostaa rakosysteemin taakse diffraktiokuvion, jossa eri matkan kulkeneet valoaallot summautuvat toisiaan joko vahvistaen tai heikentäen.
-
Interferenssi ohuissa kalvoissa: kalvon eri pinnoilta heijastuvassa valossa havaitaan värejä, jotka johtuvat toisten aallonpituuksien voimistumisesta ja toisten heikkenemisestä eripituisen matkan kulkeneiden aaltojen superposition vuoksi.
-
Kaksi peräkkäin asetettua polarisaatiosuodatinta: Kun toista kierretään, havaitaan, että läpi pääsevän valon määrä muuttuu. Valolla on siis ominaisuus, joka liittyy etenemissuuntaan nähden poikittaiseen suuntaan. Aaltomallin mukaan kyseessä on sähkömagneettisen aaltoliikkeen sähkökentän värähtelysuunta.
-
Myös polarisoituminen heijastuksessa, sironnassa, kahtaistaittavassa kiteessä: Esimerkiksi sironnassa aaltoluonne ilmenee siten, että aineeseen saapuva valo saa rakenneosat värähtelemään liikesuuntaan nähden kohtisuorassa suunnassa. Näin syntyvä sirontasäteily on polarisoitunutta saapuvan valon suuntaan nähden kohtisuoraan.
-
Valon taittuminen: Esimerkiksi ilman ja veden rajapinnassa valo taittuu niin, että valonsäteen ja pinnan normaalin välinen kulma on vedessä pienempi kuin ilmassa. Kulmien sinien suhde on aineparikohtainen vakio. Ilmiö selittyy valon aaltoluonteella, kun valon eteneminen mallinnetaan Huygensin periaatteen mukaisesti aaltorintamana. Sen jokainen piste lähettää alkeisaaltoja, joiden superpositio muodostaa uuden aaltorintaman. Taittumisen suunnasta ja aaltomallista saadaan ennuste, että valon nopeus on vedessä pienempi kuin ilmassa. Tämä on todettu mittauksilla, joten aaltomalli on pätevä kuvaamaan taittumista.
Pisteytys:Jokaisesta oikeasta kokeesta tai tilanteesta. (1 p.)
On annettu oikea selitys. (2 p.)
Jos selityksessä on virheitä tai puutteita, vähennetään yksi piste.
Jos on annettu enemmän kuin kaksi koetta tai tilannetta, arvostellaan kaksi huonointa.
Tyypillisiä virheitä:
Ei kerrota kokeesta vaan pelkästään ilmiöstä.
8.2 Sähkömagneettinen säteily käyttäytyy hiukkasten tavoin, eli säteilyn vuorovaikutus aineen kanssa muistuttaa paikallisesti tai ajallisesti toisistaan erottuvia hiukkasten osumia. Tämä voidaan havaita suoraan, tai sitten ilmiön selittävä malli edellyttää, että energia ja liikemäärä siirtyvät säteilystä aineeseen samaan tapaan kuin hiukkasten törmäyksissä. Anna yksi esimerkki kokeesta tai tilanteesta, jossa tällaista käyttäytymistä esiintyy. Kerro, miten säteilyn käyttäytyminen selittää havaitun ilmiön tai ilmiöt. 3 p.
Esimerkkejä:
-
Suunnataan hyvin heikko valo osumaan ilmaisimeen, joka voi olla joko valokuvausfilmi tai sähköinen laite, kuten valomonistinputki tai herkkä kuva-anturi. Heikko valo tuottaa filmille erillisiä, pistemäisiä jälkiä. Valomonistinputkesta saadaan sähköisiä pulsseja, jotka vastaavat ilmaisimen havaitsemia ”valohiukkasia” eli fotoneja. Kuva-anturilla taas havaitaan vuorovaikutusten erillisyys sekä ajan että paikan suhteen. Tyypillisesti koejärjestelyssä halutaan samalla näkyviin myös valon aaltoluonne, jolloin valon reitillä on kaksoisrako. Tällöin esimerkiksi filmille syntyy yksittäisten pisteiden muodostama kaksoisraon diffraktiokuvio.
-
Valosähköisessä ilmiössä metallikappaleeseen osuva valo irrottaa metallista elektroneja. Tämä havaitaan joko kappaleelle annetun negatiivisen varauksen häviämisenä tai valokennossa elektrodilta toiselle kulkevana sähkövirtana. Jotta elektroneja irtoaisi, valon aallonpituuden täytyy olla tiettyä metallista riippuvaa raja-arvoa pienempi. Jos aallonpituus on raja-arvoa suurempi, valon intensiteetin kasvattaminen ei saa elektroneja irtoamaan. Ilmiön selitys edellyttää, että valo vuorovaikuttaa metallin elektronien kanssa tavalla, joka muistuttaa hiukkasten törmäyksiä.
-
Comptonin sironnassa aineesta sironneessa röntgensäteilyssä havaitaan alkuperäisen aallonpituuden lisäksi toinen, suurempi aallonpituus, joka poikkeaa alkuperäisestä aallonpituudesta sitä enemmän, mitä suurempaan kulmaan säteily on sironnut. Tämänkin ilmiön selitys edellyttää, että säteily on vuorovaikutuksessa aineen elektronien kanssa hiukkasten kimmoista törmäystä muistuttavalla tavalla, jossa energia ja liikemäärä säilyvät.
Pisteytys:
Oikeasta kokeesta tai tilanteesta. (1 p.)
On annettu oikea selitys. (2 p.)
Jos selityksessä on virheitä tai puutteita, vähennetään yksi piste.
Jos on annettu enemmän kuin yksi koe tai tilannetta, arvostellaan huonoin.
Tyypillisiä virheitä:
Ei kerrota kokeesta vaan pelkästään ilmiöstä.
8.3 Sähkömagneettisen säteilyn energia on kvantittunut, eli säteilystä voi siirtyä energiaa aineeseen vain annoksina, joiden suuruus riippuu säteilyn taajuudesta. Anna kaksi esimerkkiä kokeista tai tilanteista, joissa tällaista käyttäytymistä esiintyy. Kerro kummastakin esimerkistä, miten säteilyn käyttäytyminen selittää havaitun ilmiön tai ilmiöt. 6 p.
Sähkömagneettisen säteilyn energian kvantittuminen tarkoittaa, että energiaa voi siirtyä säteilyn ja aineen välillä vain tietynsuuruisina annoksina. Tähän sisältyy ajatus, että itse säteily koostuu aaltopaketeista, fotoneista, joilla on tietty energia. Esimerkiksi sopivat kokeet, joissa esiintyvät ilmiöt selittävä malli edellyttää tätä.
-
Valosähköinen ilmiö: Energiaa siirtyy säteilystä elektroneille kvantteina, joiden energia on E =h f. Elektronin irrottamiseen metallista tarvitaan vähintään metallille ominaisen irrotustyön suuruinen energia. Jos säteilyn kvanttien energia on tätä pienempi, elektroneja ei irtoa, vaikka säteilyn intensiteetti olisi kuinka suuri.
-
Comptonin sironta: Tässäkin energiaa siirtyy saapuvan säteilyn fotonista elektronille kvanttina, jonka energia on E_1 =h f_1. Samanaikaisesti elektroni lähettää fotonin, jonka energia on E_2 =h f_2. Energioiden erotus E_1 -E_2 =h (f_1 -f_2) jää elektronille. Sen, että sironneen säteilyn fotonien energia riippuu sirontakulmasta, selittää malli, jossa energian kvantittumisen lisäksi myös säteilyn liikemäärä on kvantittunut.
-
Parinmuodostus, jossa syntyy hiukkanen–antihiukkanen-pareja: Esimerkiksi suurienerginen gammasäteily tuottaa elektroni–positroni-pareja. Ilmiö havaittiin ensin sumukammiossa hiukkasparin jättäminä jälkinä. Selittävän mallin mukaan gammasäteilyn fotonin energia E =h f muuttuu lain E =m c^2 mukaisesti hiukkasparin kokonaismassan energiaksi. Gammasäteilyn taajuuden ja sen myötä fotonin energian täytyy olla tarpeeksi suuri, että ilmiö voi tapahtua.
-
Luminesenssi: Ilmiö esiintyy esimerkiksi loisteaineella päällystetyllä varjostimella. Kun sitä valaistaan tarpeeksi lyhytaaltoisella valolla, varjostimen aine alkaa lähettää valoa. Saapuva valo siirtää loisteaineen atomeja matalammilta viritystiloilta korkeammille, ja loiste syntyy viritystilojen purkautuessa. Atomin virittyminen tilalta toiselle vaatii tilojen erotuksen suuruisen energiakvantin. Jos tuleva valo ei sisällä tarpeeksi lyhytaaltoisia fotoneja, virittymistä ei tapahdu eikä luminesenssia havaita.
-
Spektri: Koe, jossa mitataan absorptiospektri tai emissiospektri, jos kokelas on pystynyt sitomaan selityksen fotoneihin.
Pisteytys:
Jokaisesta oikeasta kokeesta tai tilanteesta. (1 p.)
On annettu oikea selitys. (2 p.)
Jos selityksessä on virheitä tai puutteita, vähennetään yksi piste.
Jos on annettu enemmän kuin kaksi koetta tai tilannetta, arvostellaan kaksi huonointa.
Tyypillisiä virheitä:
Ei kerrota kokeesta vaan pelkästään ilmiöstä.
Osa 3: 20 pisteen tehtävät
9. Kalan uimarakko 20 p.
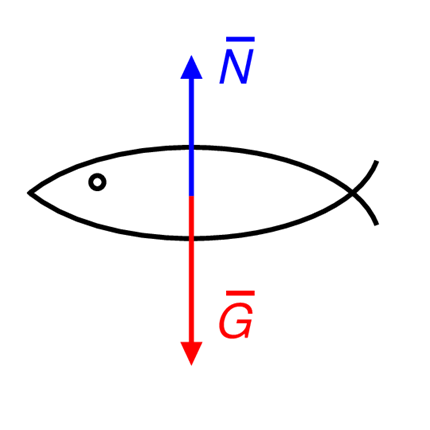
Monet kalalajit pystyvät säätelemään uimasyvyyttään niin kutsutun uimarakon avulla. Uimarakko (kuva ) on ruumiinontelon yläosassa oleva elin, joka sisältää ilmaa. Uimarakolla on joustavat seinät, jotka supistuvat ja laajenevat ympäröivän paineen vaikutuksesta. Eri syvyyksissä on eri vedenpaine, mikä vaikuttaa kalan sisäiseen paineeseen, jolloin myös uimarakon tilavuus muuttuu. Kalan kokonaistilavuus muuttuu yhtä paljon kuin uimarakon tilavuus, minkä seurauksena kalaan vaikuttava noste muuttuu. Kala pystyy kuitenkin vaikuttamaan uimarakon tilavuuteen: kaasurauhasten avulla kala voi erittää vereensä liuennutta ilmaa rakkoon tai vastaavasti vähentää ilmarakossa olevan ilman määrää, jolloin uimarakon ja koko kalan kokonaistilavuus muuttuu.
Seuraavissa osatehtävissä tarkastellaan kalaa, jonka uimarakon tilavuus on 0,079 dm^3 ja ruumiin kokonaistilavuus 0,623 dm^3 silloin, kun kala on juuri merenpinnan alapuolella. Ilmanpaine pinnalla on 101,3 kPa, ja ilman moolimassa on 29,0 g/mol. Veden lämpötila pinnalla on 17,7 ^@ C, ja veden tiheys pysyy likimain muuttumattomana 1,0 kg/dm^3 syvyydestä ja lämpötilasta riippumatta.
9.1 Juuri merenpinnan alapuolella tasapainossa kelluva kala pelästyy, ui nopeasti 7,6 metrin syvyyteen ja pysähtyy hetkellisesti. Kala on epätasapainossa, koska ilman määrä uimarakossa ja kalan lämpötila eivät nopean uinnin aikana ole ehtineet muuttua. Piirrä pysähtyneen kalan voimakuvio 7,6 metrin syvyydessä ja määritä kalaan vaikuttavan kokonaisvoiman suunta ja suuruus. 8 p.
Kalaan vaikuttavat painovoima ja noste, eli kokonaisvoima on sum vec F = vec G +vec N, jossa voimien suunnat ovat vastakkaisia. Määritetään positiivinen suunta alaspäin, jolloin F =G -N. Voimakuvioksi saadaan seuraava:
Kokonaisvoima juuri merenpinnan alapuolella on F_0 =G -N =0 --> m g -~r V_0 g =0 eli m g =~r V_0 g jossa V_0 on kalan kokonaistilavuus ja m on kalan massa.
Sukelluksessa ulkoinen paine ja kalan tilavuus muuttuvat, jolloin kokonaisvoima on F_1 =m g -~r V_1 g =~r V_0 g -~r (V_0 -~DV) g=~r ~DV g, jossa ~DV on kalan kokonaistilavuuden muutos.
Normaaliolosuhteissa ilma käyttäytyy kuten ideaalikaasu, joten ideaalikaasun tilanyhtälön avulla voidaan ratkaista tilavuuden muutos. Lämpötila ja ainemäärä pysyvät muutoksessa vakiona, joten pV\ = vakio. Näin ollen p_0 V'_0 =p_1 V'_1 eli V'_1 =V'_0 p_0/p_1, jossa p on ulkoinen paine ja V' on uimarakon tilavuus eri tilanteissa. Kalan tilavuuden muutos on yhtä suuri kuin uimarakon tilavuuden muutos eli ~DV =V'_0 -V'_0 p_0/p_1.
Ulkoinen paine juuri pinnan alapuolella, p_0 on yhtä suuri kuin ilmanpaine, kun taas 7,6 metrin syvyydessä kokonaispaineeseen lisätään myös hydrostaattinen paine, ~r g h_1, jolloin tilavuuden muutokseksi saadaan ~DV =V'_0 (1 -p_0/(p_0 +~r g h_1)).
Kokonaisvoimaksi 7,6 metrin syvyydessä saadaan F_1=\rho g V_0'\Bigl(1-\frac{p_0}{p_0+\rho gh_1}\Bigr) =1,\!00\,\frac{\rm kg}{\rm{dm}^3}\cdot 9,\!81\,\frac{\rm m}{\rm{s}^2}\cdot0,\!079\,\rm{dm}^3\Bigl(1-\frac{101300\,\rm{Pa}}{101300\,\rm{Pa}+1000\,\frac{\rm kg}{\rm{m}^3}\cdot 9,81\,\frac{\rm m}{\rm{s}^2}\cdot 7,6\,\rm{m}}\Bigr) =0,\!32856515808\,\rm{N}\approx 0,\!33\,\rm{N}.
Kokonaisvoima on 0,33 N, ja sen suunta on alaspäin.
(Tasapainotilanteessa, juuri merenpinnan alapuolella, kalaan vaikuttava noste oli N =~r V_0 g ~~6,11 N, joten uudessa tilanteessa noste on noin 0,3286 N/6,112 N ~~5 % pienempi kuin kalan paino.)
Pisteytys:
Oikein piirretty voimakuvio, jossa noste ja paino on nimetty sanallisesti tai symbolilla (2 p.)
Voimakuviosta tehdään seuraavat vähennykset:
-
Vakavasta virheestä (puuttuvat, ylimääräiset tai väärään suuntaan osoittavat voimat) vähennetään kaksi pistettä.
-
Merkittävästä virheestä (voiman nimi tai symboli puuttuu) vähennetään yksi piste.
On kirjoitettu suureyhtälö kokonaisvoimalle 7,6 m syvyydessä painon ja nosteen avulla. (2 p.)
On kirjoitettu suureyhtälö kalan tilavuuden muutokselle paineen avulla tai saatu tilavuuden muutos oikein laskettua. (2 p.)
On annettu oikea voiman suuruus 2-3 merkitsevän numeron tarkkuudella (1 p.) ja voiman oikea suunta (1 p.)
9.2 Tämän jälkeen kala jää 7,6 metrin syvyyteen, jossa lämpötila on 11,3 ^@C. Kalan ruumiinlämpötila tasaantuu ympäristön lämpötilaan. Paineen lisäksi myös lämpötilan muutos vaikuttaa uimarakossa olevan ilman tilavuuteen. Kuinka paljon lisää ilmaa kala joutuu erittämään uimarakkoon, jotta se pystyy kellumaan tasapainossa 7,6 metrin vakiosyvyydellä? Ilmoita tulos milligrammoina. 6 p.
Ideaalikaasun tilanyhtälön, p V =n R T, avulla voidaan ratkaista tarvittavan lisäilman massa tilanteessa, jossa uimarakon sisällä olevaan kylmempään ilmaan vaikuttaa suurempi paine. Uimarakossa olevan ilman alkuperäinen ainemäärä oli n_0 =(p_0 V'_0) /(R T_0) ja kellumiseen tarvittava ainemäärä on n_1 =(p_1 V'_1) /(R T_1), jolloin lisäilman ainemäärä on ~Dn =n_1 -n_0 =(p_1 V'_1) /(R T_1) - (p_0 V'_0) /(R T_0)
Kala kelluu taas, kun uimarakon tilavuus on sama kuin se oli juuri merenpinnan alapuolella eli V'_0 =V'_1, joten saadaan ~Dn =V'_0 /R (p_1/T_1 -p_0/T_0) =V'_0/R ((p_0 +~r g h_1) /T_1 -p_0/T_0).
Lisäilman massa on ~Dm =~Dn *M ==M V'_0/R ((p_0 +~r g h_1) /T_1 -p_0/T_0), jossa M =29,0 g/mol on ilman moolimassa, V'_0 =0,079 dm^3 =0,000079 m^3 on uimarakon alkuperäinen tilavuus, T_1 =273,15 K +11,3 K =284,45 K on lämpötila 7,6 metrin syvyydessä, T_0 =273,15 K +17,7 K =290,85 K on lämpötila pinnalla ja h_1 =7,6 m on kalan syvyys merenpinnan alapuolella.
Saadaan ~Dm =0,07438507719 g ~~74 mg.
Pisteytys:
On todettu sanallisesti tai käy ilmi laskusta, että kalan tilavuus pitää olla yhtä suuri kuin kalan kelluessa juuri pinnan alapuolella. (2 p.)
On kirjoitettu suureyhtälö massan muutokselle paineen ja tilavuuden avulla. (2 p.)
On annettu oikea vastaus massan muutokselle 2-3 merkitsevän numeron tarkkuudella välillä 74 mg - 75 mg. (2 p.)
Tyypillinen virhe:
On laskettu massan muutos ottamatta huomioon lämpötilan muutosta ja saatu tulokseksi ~Dm =0,07222569516 g ~~72 mg.
9.3
Kaikuluotauksessa veteen lähetetyt ääniaallot heijastuvat kaloista (kuva ). Pienetkin kalat voidaan havaita selkeästi, jos ääniaallot resonoivat kalojen uimarakossa olevan ilman kanssa. Tällaista resonanssissa olevaa uimarakkoa voidaan yksinkertaistetusti tarkastella molemmista päistä suljettuna putkena.
Eräs kala näkyi selkeästi luotaimessa, kun äänen taajuus oli pienimmillään 2,4 kHz. Laske kalan uimarakon suurimman ontelon pituus ja kalan etäisyys kaikuluotaimesta, kun kalasta heijastunut ääni palasi 12 ms lähettämisen jälkeen. Äänen nopeus ilmassa on 343 m/s ja vedessä
1 484 m/s.
6 p.
Resonanssia esiintyy, kun uimarakkoon syntyy seisova aalto. Suljetun putken molemmissa päissä pitää silloin olla solmukohdat, joten resonanssia synnyttävän äänen aallonpituus voi suurimmillaan olla ~l =2 l.
Aaltoyhtälön, v =~l f, avulla voidaan ilmaista putken pituus taajuuden funktiona l =1/2 ~l =v /(2 f).
Äänen nopeus uimarakossa on v =343 m/s ja taajuus, f =2,4 kHz, pysyy samana väliaineesta riippumatta. Uimarakon pituudeksi saadaan l =343 m/s /(2 *224 kHz) =0,071458333 m ~~7,1 cm.
Kalan etäisyys kaikuluotaimesta on puolet ääniaallon etenemästä matkasta x =1/2 s =1/2 v t, jossa v =1484 m/s on äänen nopeus vedessä. Etäisyydeksi saadaan x =1/2 *1484 m/s *12 ms ~~8,9 m.
Pisteytys:
On mainittu sanallisesti tai kerrottu kuvassa, että uimarakkoon syntyy seisova aalto tai että uimarakossa olevassa aallossa on solmu molemmissa päissä. (2 p.)
On annettu oikea vastaus uimarakon pituudelle 2-3 merkitsevän numeron tarkkuudella välillä 7,14 cm – 7,15 cm. (2 p.)
On annettu oikea vastaus kalan etäisyydelle 2-3 merkitsevän numeron tarkkuudella välillä 8,59 m – 8,91 m. (2 p.)
Tyypillisiä virheitä:
-
On annettu uimarakon pituudeksi äänen aallonpituus.
-
On ajateltu kalan etäisyydeksi edestakainen matka.
-
On laskettu etäisyyttä siten, että osan ajasta ääni liikkuu ilmarakossa ja saatu hiukan lyhyempi etäisyys. Nämä etäisyydet mahtuvat kuitenkin hyväksytyn vastauksen rajojen sisäpuolelle.
10. Johdonsuojakatkaisija 20 p.
10.1 Verkkovirtaan kytketyt vialliset sähkölaitteet saattavat aiheuttaa kotona sähkötapaturmia ja muita vahinkoja. Miksi sähköisku on ihmiselle vaarallinen? Millaisia muita onnettomuuksia viallinen sähkölaite voi kotona aiheuttaa? 4 p.
Verkkovirtaan kytketty viallinen laite saattaa aiheuttaa sähköiskun, jolloin ihmisestä tulee virtapiirin osa ja sähkövirta kulkee hänen lävitseen. Sähkövirta voi häiritä ihmisen hermoston toimintaa tai aiheuttaa palovamman. Viallinen laite saattaa myös kuumentua liikaa ja aiheuttaa kotona tulipalon.
Pisteytys:
On mainittu sähkövirran vaikutus sydämeen tai hermostoon tai mainittu kouristukset tai palovammat. (2 p.)
On mainittu laitteen aiheuttama tulipalo. (2 p.)
Tyypillisiä virheitä:
On väitetty, että sähköisku aiheuttaa sydänkohtauksen.
10.2 Johdonsuojakatkaisijan laukaisukäyrässä (kuva ) voidaan erottaa kaksi aluetta, niin sanotut terminen (T) ja magneettinen (M) alue. Millaisiin virtapiirin vikoihin laukaisukäyrän näillä alueilla varaudutaan? 6 p.
Termisellä alueella sähkövirta on vain muutamia kertoja katkaisijan nimellisvirran suuruinen. Liian pitkään jatkuessaan tällaiset tapaukset johtavat piirin ylikuumenemiseen ja lopulta tulipaloon. Termisellä alueella varaudutaan siis tilanteeseen, jossa virtapiirin jokin laite käyttää nimellisvirtaa suurempaa sähkövirtaa pitkän aikaa.
Magneettisella alueella sähkövirrat ovat paljon suurempia kuin katkaisijan nimellisvirta ja sähkövirta katkaistaan hyvin nopeasti. Magneettisella alueella varaudutaan siis tapauksiin, joissa piiriin syntyy äkillisesti hyvin suuri sähkövirta, eli esimerkiksi oikosulkuihin.
Pisteytys:
On tunnistettu, että termisellä alueella varaudutaan vikaan, jossa virta on hieman katkaisijan nimellisvirtaa suurempi (1 p.), ja kerrottu, että tällainen vika tuottaa ongelmia jatkuessaan pitkään. (2 p.)
On tunnistettu, että magneettisella alueella varaudutaan vikaan, jossa virta on merkittävästi katkaisijan nimellisvirtaa suurempi (1 p.), ja kerrottu, että tällöin katkaiseminen tulee tehdä nopeasti tai että tällä varaudutaan oikosulkuun. (2 p.)
Mikäli virran suuruutta ei käsitellä oikein, voi kummankin vian keston tunnistamisesta saada yhden pisteen.
Tyypillisiä virheitä:
-
Väitetään katkaisemisen mittaavan termisellä alueella lämpötilaa ja magneettisella alueella magneettikenttää.
-
Sekoitetaan johdinten katkeaminen ja oikosulku.
-
Ei liitetä vastausta virtapiirin vikoihin.
10.3 Verkkovirtapiirissä johdonsuojakatkaisijan nimellisvirta on 16 A. Piiriin kytkettyyn laitteeseen tulee vika, ja virtapiiriin syntyy 32 A:n sähkövirta. Kuinka paljon sähköenergiaa ehtii siirtyä laitteeseen ennen sähkövirran katkeamista? 6 p.
Sähköenergian teho on P =U I, joten laitteeseen siirtyneen energian suuruus on E =P t =U I t, missä johdonsuojakatkaisijan laukaisukäyrästä luettuna 10 <= t <= 45 s.
Energiaa siirtyy vähintään E_1 =U I t_1 =230 V *32 A *10 s =73.600 J ~~74.000 J.
Energiaa siirtyy enintään E_2 =U I t_2 =230 V *32 A *45 s =331.210 J ~~330.000 J.
Pisteytys:
On luettu kuvaajasta oikea ylä- tai alarajaa vastaava aika-arvo (2 p.) ja saatu edellisen perusteella yksi oikea energian arvo välillä 70 kJ - 384 kJ. (2 p.)
On laskettu oikein 1- 3 merkitsevän numeron tarkkuudella sekä ylärajan arvo välille 290 kJ - 384 kJ että alarajan arvo välille 70 kJ - 80 kJ. (2 p.)
Tyypillisiä virheitä:
On laskettu siirtyvän varauksen arvo.
10.4 Johdonsuojakatkaisija pystyy havaitsemaan vain tilanteet, joissa virtapiirin sähkövirta kasvaa liian suureksi. Verkkovirtapiirissä voi kuitenkin olla muitakin vikoja, jotka aiheuttavat vaaratilanteita tai ongelmia piirin toiminnalle, jollei niiltä suojauduta. Mitä muita suojaamista vaativia vikoja verkkovirtapiirissä voi olla? Mainitse vähintään kaksi. 4 p.
Johdonsuojakatkaisijalta jää havaitsematta joitain piirin virhetilanteita. Esimerkkejä näistä tilanteista:
-
Piiriin syötetty ja piiristä palaava sähkövirta eivät ole yhtä suuria. Puuttuvaa sähkövirran osaa kutsutaan vuotovirraksi, ja sen havaitsemiseen tarvitaan erillinen laite, vikavirtakytkin.
-
Piirin jännite ja sähkövirta eivät ole samassa vaiheessa. Tällöin piirissä kulkee loisvirta, jota johdonsuojakatkaisija ei pysty havaitsemaan.
-
Kolmivaihevirran yksi vaihe putoaa nollaan.
-
Jännitteen laadussa on pieniä häiriöitä, kuten kohinaa tai muita lyhytaikaisia poikkeamia sinimuotoisesta jännitteestä. Koska johdonsuojakatkaisija tarkkailee vain sähkövirran suuruutta, se ei pysty havaitsemaan tällaisia häiriöitä.
Pisteytys:
Jokaisesta oikeasta viasta tai tilanteesta (2 p.). Arvostellaan kaksi parasta.
Tyypillisiä virheitä:
Väitetään viaksi sähkövirran katkeamista tai laitteen rikkoutumista.
Väitetään viaksi sähköiskun saamista. Se voi olla vian seuraus.
Väitetään viaksi oikosulkua, jolta johdonsuojakatkaisija suojaa.
11. Suprajohtavuus 20 p.
11.1 Miksi magneetti nousee ilmaan? Miksi ilmiötä ei voi selittää induktiolain avulla? 5 p.
Induktiolain mukaan virtasilmukkaan syntyy induktiojännite, kun magneettivuo silmukan läpi muuttuu ajan funktiona. Videossa esitetyssä tilanteessa magneetti on alun perin paikallaan suprajohtavaksi muuttuvan kiekon päällä. Magneettivuo kiekon läpi on siis vakio ja magneettivuon muutos per aikayksikkö nolla. Suprajohteen pintaan muodostuvia pyörrevirtoja ei siten voida selittää klassisen sähkömagneettisen induktion avulla.
Kun kiekko jäähdytetään, se muuttuu suprajohtavaksi. Suprajohteen perusominaisuuksiin kuuluu se, että johde sulkee ulkoisen magneettikentän pois pinnassaan olevien pyörrevirtojen aiheuttamalla vastakkaissuuntaisella magneettikentällä. Vastakkaissuuntaiset magneettikentät hylkivät toisiaan, joten magneetti nousee ilmaan. Koska suprajohde sulkee ulkoisen magneettikentän pois, magneettivuo suprajohtavan kappaleen läpi muuttuu, mutta se muuttuu vasta sen jälkeen, kun pyörrevirrat ovat syntyneet.
Pisteytys:
On perusteltu, että induktiolaki ei selitä ilmiötä sillä, että magneetti ei liiku (2 p.)
On kerrottu, että ulkoinen magneettikenttä saa suprajohteessa aikaan pyörrevirtoja ja nämä pyörrevirrat synnyttävät magneettikentän (2 p.)
On perusteltu magneetin nouseminen ilmaan joko hylkivällä magneettisella voimalla, toisiaan hylkivillä magneettisilla navoilla tai kertomalla syntyvän voiman olevan yhtä suuri kuin kiekon paino. (1 p.)
11.2 Mitä tapahtuu, jos leijuvan magneetin pohjoisnapa käännetään kohti suprajohdetta? Jatkaako magneetti leijumista vai putoaako se alas suprajohteen pinnalle? 4 p.
Aineiston mukaan suprajohde hylkii aina ulkoisia magneettikenttiä muodostamalla pyörrevirtoja pinnalle. Tämä tapahtuu riippumatta siitä, onko magneetin pohjoisnapa vai etelänapa suunnattu kohti suprajohdetta. Jos magneetti käännetään toisinpäin, myös suprajohteen pinnassa olevien pyörrevirtojen suunta kääntyy, jolloin suprajohteen ja magneetin hylkivä voima pysyy ennallaan ja magneetti jatkaa leijumistaan.
Pisteytys:
On vastattu, että magneetti jatkaa leijumista. (1 p.)
On perusteltu oikea vastaus kertomalla pyörrevirtojen suunnan kääntymisestä vastakkaiseksi. (3 p.)
11.3 Millaisia hyötyjä saavutettaisiin, jos suprajohtavuus saataisiin aikaan huoneenlämpötilassa? 4 p.
Sähkönsiirrossa on aina muutaman prosentin vastushäviö. Jos voitaisiin käyttää suprajohteita, sähköä voisi siirtää ilman energiahäviöitä, mikä säästäisi vuosittain paljon rahaa. Kaapelit voisivat olla melko ohuita, koska niiden sähkövastus on nolla.
Kaikissa elektronisissa laitteissa sähkövirroista johtuvat tehonhäviöt lämmittävät komponentteja. Tämä voi johtaa ylikuumenemiseen. Siksi laitteisiin on usein lisätty tuuletusaukkoja ja jäähdytysrimoja. Jos johtimet olisivat suprajohtavia, tuuletusaukkoja ja rimoja ei tarvittaisi. Laitteet voisivat olla pienempiä, ja komponentit voisi asentaa lähemmäs toisiaan piirilevyillä.
Pisteytys:
On tunnistettu pienemmät energia- tai tehohäviöt energian siirrossa. (2 p.)
Edellisen avulla on perusteltu yksi järkevä hyöty, esimerkiksi laitteiden, kustannusten tai jäähdytystarpeen pieneneminen tai ohuempien tai pidempien johtimien käyttömahdollisuus (2 p.)
Tyypillisiä virheitä:
-
Selitetään häviöitä liittämättä niitä energiaan.
-
Tarjotaan hyödyksi pelkkää sovellusta.
-
Tarjotaan mielikuvituslaitteita.
11.4 Minkälaisia materiaaliin liittyviä ongelmia korkean lämpötilan suprajohteilla on? Voiko ohut suprajohtava lanka kuljettaa kuinka suuren virran tahansa? 4 p.
Koska materiaalit ovat keraamisia, niistä on hankala tehdä kaapeleita. Kaapeleiden tulee kestää mekaanisia rasituksia katkeamatta, mihin keraamiset materiaalit harvemmin pystyvät. (Esimerkiksi videossa näkyvä suprajohtava kiekko on täynnä halkeamia.)
Suprajohtavan kaapelin kriittistä virrantiheyttä ei myöskään saa ylittää. Kriittinen virrantiheys kerrottuna kaapelin poikkipinta-alalla määrittää kaapelissa kulkevan suurimman mahdollisen virran, eli kaapelilla tulisi olla tietty minimipaksuus, jos siinä halutaan kuljettaa voimakkaita virtoja. Mikäli virrantiheys ylittyy, kaapeli lämpenee ja muuttuu hetkessä normaaliksi, mikä voi johtaa sen sulamiseen.
Pisteytys:
On tunnistettu materiaalin tai siitä valmistettujen johtimien alttius rikkoutumiselle käyttämällä jotain muuta sanaa kuin aineistossa annettu "hauras". (2 p.)
On vastattu jälkimmäiseen kysymykseen "ei" ja perusteltu vastaus kytkemällä toisiinsa kaapelissa kulkeva virta, kriittinen virrantiheys ja kaapelin poikkipinta-ala (2 p.)
Tyypillinen virhe:
Pelkkä tekstin kopiointi aineistosta.
11.5 Miksi tyypin II suprajohteita käytetään suprajohtavissa magneeteissa? 3 p.
Suprajohtavan käämin luoma voimakas magneettikenttä kohdistuu myös suprajohtavaan lankaan itse käämissä. Aineiston mukaan tyypin I suprajohteilla Bc on arvoltaan pieni. Mikäli se ylittyy käämissä, johdelanka siirtyy yhtäkkiä normaaliin tilaan ja johteessa kulkeva virta saattaa vaurioittaa lankaa. Tyypin II suprajohteen tapauksessa johdelanka pysyy suprajohtavana, kunhan magneettivuon tiheys ei ylitä arvoa Bc2 käämin sisällä. Aineiston mukaan tyypin II suprajohteilla Bc2:n arvo on suuri. Tyypin II suprajohteita on siksi turvallisempaa käyttää käämeissä kuin tyypin I johteita.
Pisteytys:
On tunnistettu oikein toinen tai molemmat seuraavista (3 p.)
-
käämin oma magneettikenttä vaikuttaa käämiin ja aiheuttaa kentän, jonka voimakkuus ei saa ylittää kriittistä kenttää
-
tyypin II suprajohde kestää suurempia magneettikenttiä kuin tyypin I suprajohde.
Mikäli kumpaakaan ei ole tunnistettu, mutta on kerrottu aineistosta poimittuja oikeita asioita tyypin II suprajohteen käyttäytymisestä magneettikentässä annetaan yksi piste.