Beskrivningar av goda svar: SV – Fysik
17.9.2025
Slutgiltiga beskrivningar av goda svar 13.11.2025
Grunderna enligt vilka bedömningen gjorts framkommer i de slutgiltiga beskrivningarna av goda svar. Uppgiften om hur bedömningsgrunderna tillämpats på examinandens provprestation utgörs av de poäng som examinanden fått för sin provprestation, de slutgiltiga beskrivningarna av goda svar och de föreskrifter gällande bedömningen som nämnden gett i sina föreskrifter och anvisningar. De slutgiltiga beskrivningarna av goda svar innehåller och beskriver inte nödvändigtvis alla godkända svarsalternativ eller alla godkända detaljer i ett godkänt svar. Eventuella bedömningsmarkeringar i provprestationerna anses vara jämställbara med anteckningar och sålunda ger de, eller avsaknaden av markeringar, inte direkta uppgifter om hur bedömningsgrunderna tillämpats på provprestationen.
I studentprovet i fysik bedöms såväl förmågan att förstå fysikaliska fakta som förmågan att tillämpa denna kunskap, i enlighet med grunderna för gymnasiets läroplan. I provet bedöms vidare examinandens förmåga att experimentellt inhämta och bearbeta kunskap. Exempel på denna förmåga är bland annat att planera experiment, att behärska användningen av de vanligaste mätinstrumenten, att presentera och tolka resultat samt att dra slutsatser. I provet bedöms även examinandens förmåga att förstå och analysera material av fysikalisk natur. Vid bedömningen uppmärksammas att svaren innehåller en saklig användning av fysikens begrepp och begreppstrukturer och att svaren presenterats logiskt samt med ett konsekvent och väldisponerat faktainnehållet.
Ett gott svar på en uppgift i fysik inkluderar motiveringar för svaret, om inget annat nämns i uppgiften. Ur det framgår att examinanden har identifierat det fysikaliska fenomenet korrekt och granskar situationen på ett fysikaliskt meningsfullt sätt. Examinanden kan beskriva den tillämpade fysikaliska modellen och motivera varför modellen kan användas i den situationen. Om svaret kräver situationsbilder, kraftfigurer, kopplingsscheman eller grafiska presentationer är de tydliga och gjorda i enlighet med de allmänna principerna som råder i fysiken. Exempelvis i kraftfigurer särskiljs de verkliga krafterna tydligt från deras vektorkomponenter.
I de uppgifter som kräver matematisk behandling ska storhetsekvationerna och formlerna motiveras på ett sätt som visar att examinanden tolkat situationen rätt utgående från fysiken. I svaret ingår även nödvändiga uträkningar och andra tillräckliga motiveringar samt ett slutresultat. Storheternas värden behöver i fysikprovet inte skrivas in synligt i formeln, om det av svaret tydligt framgår vilket talvärde och vilken enhet som används för respektive storhetssymbol. Lösningar som gjorts med hjälp av symboliska räkneprogram godkänns, så länge det av svaret framgår på vilken situation och vilka symboler i situationen svaret bygger samt att storhetsekvationen, löst för storheten som söks i uppgiften, presenteras i samband med svaret.
De allmänna riktlinjerna för poängsättning är:
- Ifall att antalet gällande siffror som ges i svaret avviker från det som anges i BGS är avdraget en poäng för varje svar.
- Om enheten för slutresultatet är felaktig eller saknas är resultatet felaktigt.
Del 1: 20-poängsuppgift
1. Uppgifter från olika delområden i fysiken 20 p.
1.1 Vad är den ungefärliga effekten för en vattenkokare i hemmets kök? 2 p.
- 1 000 W (2 p.)
1.2 Vilken är den ungefärliga laddningsströmmen för en mobiltelefon? 2 p.
- 1 A (2 p.)
1.3 Ungefär hur lång tid tar det för radiovågor att färdas från jorden till månen? 2 p.
- 1 s (2 p.)
1.4 Vilken är den ungefärliga diametern på ett hårstrå? 2 p.
- 100 ~mm (2 p.)
1.5 En okänd storhet X 4 p.
1.5.1 Använd enhetsanalys för att ta reda på enheten för storheten X. Skriv endast enheten för storheten X i svarsfältet. 2 p.
- meter (2 p.)
1.5.2 Använd enhetsanalys för att ta reda på namnet på storheten X. Skriv endast namnet på storheten X i svarsfältet. 2 p.
- sträcka (2 p.)
- längd (2 p.)
- avstånd (2 p.)
1.6 En okänd storhet Y 4 p.
1.6.1 Använd enhetsanalys för att ta reda på enheten för storheten Y. Skriv endast enheten för storheten Y i svarsfältet. 2 p.
- meter per sekund (2 p.)
1.6.2 Använd enhetsanalys för att ta reda på namnet på storheten Y. Skriv endast namnet på storheten Y i svarsfältet. 2 p.
- hastighet (2 p.)
- fart (2 p.)
1.7 En okänd storhet Z 4 p.
1.7.1 Använd enhetsanalys för att ta reda på enheten för storheten Z. Skriv endast enheten för storheten Z i svarsfältet. 2 p.
- sekund (2 p.)
1.7.2 Använd enhetsanalys för att ta reda på namnet på storheten Z. Skriv endast namnet på storheten Z i svarsfältet. 2 p.
- tid (2 p.)
Även andra korrekta uttryck godkänns.
Del 2: 15-poängsuppgifter
2. En kula i ett rör 15 p.
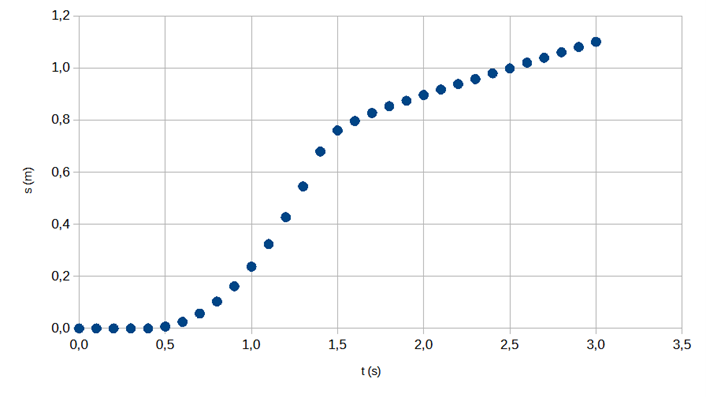
2.1 Skapa en graf av sträckan som kulan färdats som funktion av tiden med hjälp av tabell . En grafisk utjämning ska inte inkluderas i den här grafen. 4 p.
Poängsättning:
Det har presenterats en korrekt graf över sträckan som kulan färdats som funktion av tiden. (4 p.)
För grafen görs följande poängavdrag:
-
Ifall ett stapeldiagram har ritats ges noll poäng för grafen.
-
Om endast en bruten linje har ritats är avdraget två poäng.
-
Om datapunkterna har sammankopplats med en bruten linje är avdraget två poäng.
-
Om en anpassning har ritats i grafen är avdraget två poäng.
-
Om en eller flera datapunkter saknas från grafen är avdraget två poäng.
-
Om siffervärdena saknas eller är felaktiga på den ena eller på båda av axlarna är avdraget en poäng.
-
Om storhetens namn saknas eller är felaktig på den ena eller på båda av axlarna är avdraget en poäng.
-
Om enheten för storheterna saknas eller är felaktig på den ena eller på båda av axlarna är avdraget en poäng.
-
Om axlarna har ritats omvänt är avdraget en poäng.
Typiska fel:
Endast en bruten linje har ritats i grafen eller mätpunkterna har sammankopplats med en bruten linje.
En anpassning har ritats i grafen.
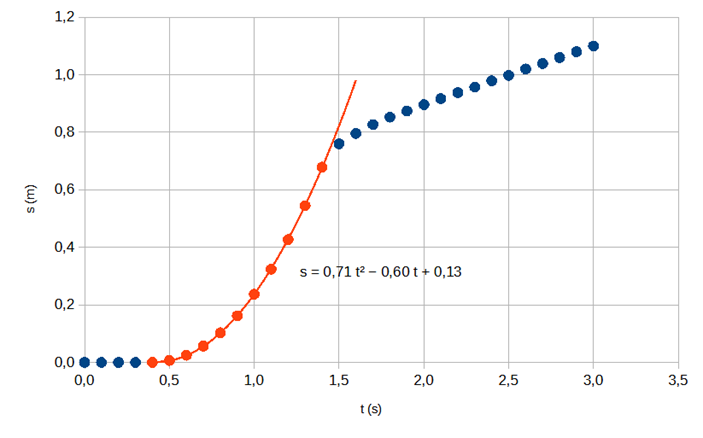
2.2 Använd din graf för att med en grafisk metod ta reda på när kulan träffar vattenytan. Välj det av tidsintervallen a–d under vilket kulan träffar vattenytan. Motivera ditt svar genom att rita en ny graf i vilken det syns en parabel som anpassats till en del av mätpunkterna. 6 p.
Kulan träffar vattenytan inom tidsintervallet b.
Motivering: Mätpunkterna för grafen s(t) i intervallet 0,4–1,4 s faller mycket exakt på en parabel som är anpassad till punkterna. Det här antyder att rörelsen i det här tidsintervallet är likformigt accelererad inom gränserna för mätnoggrannheten. Mätpunkten som finns vid tiden 1,5 sekunder faller inte på kurvan, alltså har accelerationen ändrat mellan 1,4–1,5 s. Det här beror på att kulan träffat vattnet.
(Enligt Newtons II lag är ΣF = ma, alltså måste förändringen i accelerationen orsakas av en förändring i den totala kraften. Den å sin sida beror på att kulan träffar vattnet, eftersom att i vattnet börjar kulan också påverkas av en betydande motståndskraft från mediet, utöver påverkan från gravitationen, stödkraften och friktionen.)
Poängsättning:
Den korrekta bokstaven (b) eller det korrekta tidsintervallet (1,4 s - 1,5 s) har givits. (2 p.)
Det har presenterats en graf där det till datapunkterna inom tidsintervallet t\le1{,}6~\mathrm{s} korrekt har anpassats en parabel som öppnar sig uppåt och för vilken ekvationen syns. (2 p.)
Det korrekta tidsintervallet för träffen har motiverats med avvikelsen för datapunkten från en parabel som är korrekt anpassad till mätpunkterna inom intervallet 0{,}3~\mathrm{s}\ \le t\le1{,}4~\mathrm{s}. (2 p.)
Typiska fel:
En annan funktion än en parabel har anpassats till punkterna.
Parabeln har anpassats till fel tidsintervall.
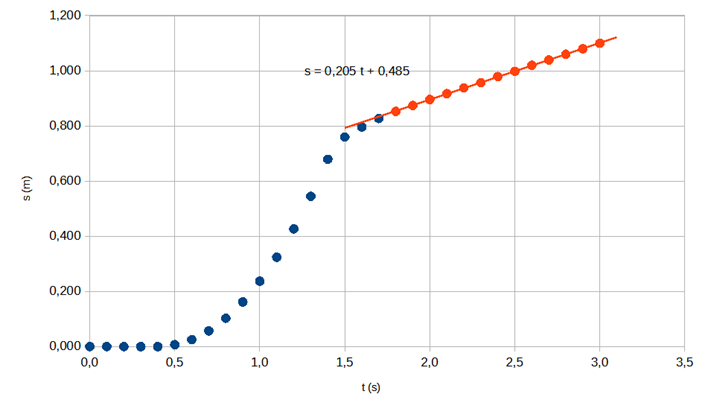
2.3 Bestäm kulans hastighet i en situation som visas i videon där kulan är i rörelse och krafterna som påverkar den är i jämvikt med varandra. 5 p.
Då kulan rör sig i vattnet är motståndskraften från mediet som påverkar kulan beroende av hastigheten. Kulans slutliga hastighet blir sådan att krafterna som verkar på kulan balanserar ut varandra. Därmed är kulans acceleration noll och dess hastighet konstant. Den här situationen motsvaras av den del av grafen där datapunkterna är på en linje.
Kulans hastighet är riktningskoefficienten för linjen.
Genom att anpassa en rät linje får vi v = 0,205 m/s.
Poängsättning:
Det har berättats att kulans rörelse är likformig, kulans hastighet är konstant eller att kulans acceleration är noll. (1 p.)
Riktningskoefficienten har bestämts för ett tidsintervall där nedre gränsen är 1,5 s och övre gränsen är klart större. (2 p.)
Ett korrekt värde för hastigheten har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,20 m/s – 0,22 m/s. (2 p.)
Typiska fel:
Linjen har anpassats till fel tidsintervall.
3. Jordvärme 15 p.
3.1 Var kommer värmeenergin som är lagrad i berggrunden i huvudsak ifrån? 3 p.
Värmeenergin kommer i huvudsak från solen. Geotermiska energins andel blir betydande först vid flera kilometers djup.
Poängsättning:
Det har berättats att energin kommer från solen. (3 p.)
Det sämre svaret bedöms om fler än ett svar har givits.
Typiska fel:
Det har hävdats att energin kommer från jordens kärna.
På jordens yta marker man att temperaturen ändrar med årstiderna ända ner till ett djup på ungefär 15 meter, vilket visar solens omedelbara effekt. Vid jordytan är energiflödet från solen över tusen gånger större jämfört med flödet från jordens inre. Därför beror storleken på temperaturen vid flera hundra meters djup ännu i huvudsak på att solens uppvärmande effekt förhindrar att temperaturen sjunker då jorden strålar energi ut i rymden.
3.2 Då jordvärmesystemet tas i bruk leds 350 liter vatten med temperaturen 7,0\,^\circ\rm{C} till varmvattensbehållaren. Anläggningen värmer på 2,5 timmar upp vattnet till temperaturen 60 ^@C och förbrukar 7,4 kWh elektrisk energi för det här. Bestäm systemets värmekoefficient och beräkna effekten med vilken vattnet värms upp. 7 p.
Värmemängden som överförs till vattnet är Q =c m ~DT = c ~r V (T_2 -T_1). Vattnets densitet vid en temperatur på 7 ^@C är ~r =999,90 kg/m^3 Värmekoefficienten, det vill säga förhållandet mellan värmemängden och den elektriska energin som förbrukas är ~ä =~DQ/E =c ~r V(T_2 -T_1)/E =(4,19 kJ/(kg K) *999,90 kg/m^3 *0,35 m^3 *53 K) /7,4 kWh =77,71672755 MJ /(7,4 kW *3600 s) ~~2,9.
Vattnet värms upp med effekten P =~DQ/~Dt =77,71672755 MJ /(2,5 *3600 s) =8635,19195 W ~~8,6 kW
Poängsättning:
Ett korrekt värde för värmemängden som överförs till vattnet har givits inom intervallet 77,5 MJ - 77,8 MJ. (2 p.)
Ett korrekt värde för värmekoefficienten har med två eller tre gällande siffrors noggrannhet givits inom intervallet 2,90 - 2,92. (3 p.)
Ett korrekt värde för effekten har med två eller tre gällande siffrors noggrannhet givits inom intervallet 8,62 kW - 8,64 kW. (2 p.)
Typiska fel:
Den elektriska effekten har givits istället för uppvärmningseffekten.
Fel temperaturförändring har använts för att beräkna värmemängden som överförts till vattnet.
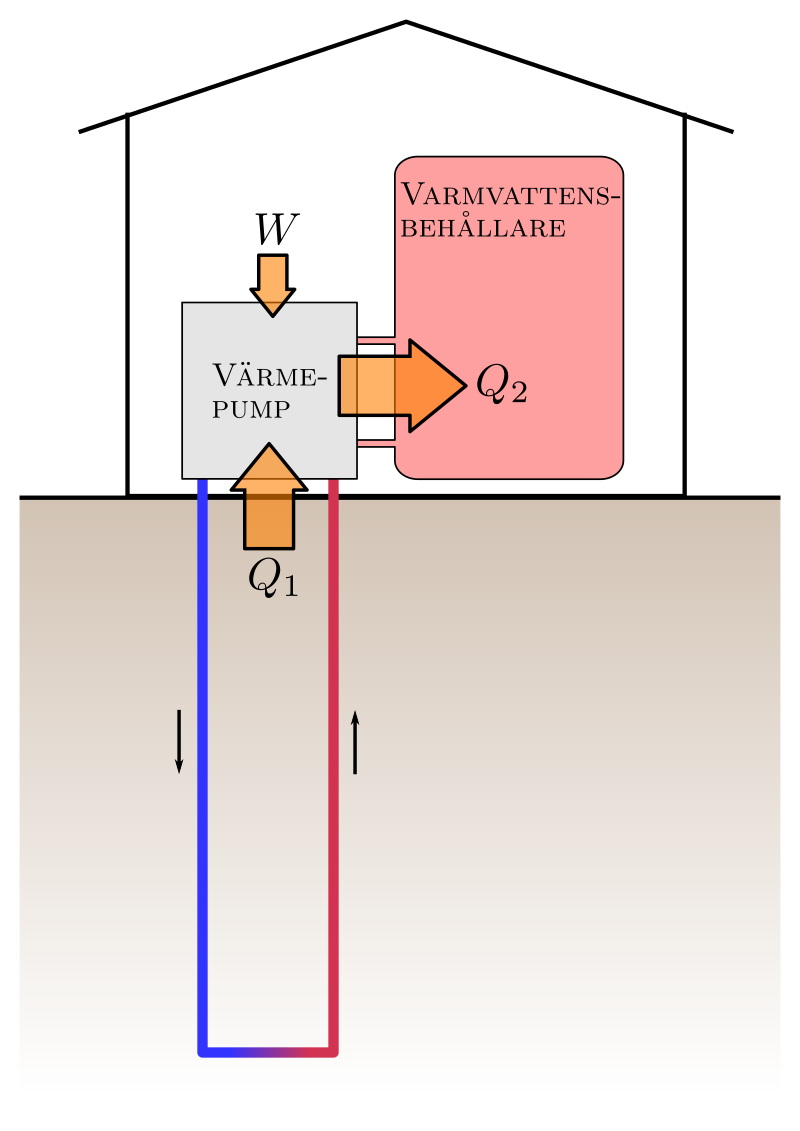
3.3 Rita ett diagram som visar värmepumpens energiflöden och namnge storheterna som förekommer i det. Skriv en ekvation som sammankopplar storheterna. Om du vill kan du använda dig av bild då du ritar diagrammet. 5 p.
Q_1 = värmemängden som överförs från jorden
Q_2 = värmemängden som överförs till vattenbehållaren
W = arbetet som värmepumpen utför med elektrisk energi
För storheterna gäller ekvationen Q_1 +W =Q_2
Poängsättning:
Ett korrekt diagram har givits. (3 p.)I det korrekta diagrammet har det visats att
-
värme överförs från jorden till pumpen,
-
värme överförs från pumpen till vattenbehållaren,
-
arbete kommer till pumpen utifrån,
och de tre ovan nämnda storheterna har namngivits korrekt.
Noll poäng ges för diagrammet om någon av de korrekta storheterna saknas eller om energi flödar i fel riktning.
En korrekt storhetsekvation som är konsistent med diagrammet har givits. (2 p.)
Typiska fel:
-
De svarta pilar som syns i bilden har betecknats med överförd energi.
-
En värmepump med varm behållare och en kall behållare har ritats, men den har inte kopplats till sammanhanget i uppgiften.
-
Värme har behandlats som en tillståndsvariabel, exempelvis genom att tala om den varma behållarens värme, eller genom att beteckna Q2 som den varma behållarens energi.
4. En benpress 15 p.
4.1 Rita en kraftfigur för kroppen som bildas av kälken och vikterna då motionären håller kälken och vikterna på plats med hjälp av sina ben. Använd bild som mall för din kraftfigur. 3 p.
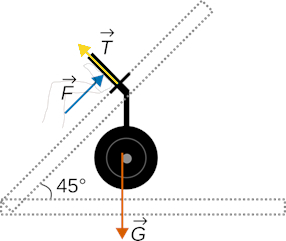 \vec T är stödkraften, \vec G är tyngden och \vec F är kraften som motionären riktar mot kälken.
Poängsättning:
\vec T är stödkraften, \vec G är tyngden och \vec F är kraften som motionären riktar mot kälken.
Poängsättning:
En korrekt ritad kraftfigur där stödkraften, tyngden och kraften som motionären riktar mot kälken har namngivits med ord eller symboler. (3 p.)
Följande poängavdrag görs från kraftfiguren:
-
För grova fel (saknade krafter, överlopps krafter eller krafter som verkar i fel riktning) är avdraget tre poäng.
-
För betydande fel (kraftens namn eller symbol saknas, krafternas summa avviker märkbart från noll, flera av krafterna har samma symbol eller namn) är avdraget en poäng per typ av fel.
-
Ifall en annan bild än den som givits använts som mall för kraftfiguren är avdraget en poäng.
Typiska fel:
-
Stödkraften har inte ritats.
4.2 Hur stor kraft bör motionären som minst rikta mot kälken för att kälken och vikterna ska hållas på plats i det övre läget? 6 p.
Tyngderna och kälken är i jämvikt.
Då friktionen inte beaktas är krafternas jämvikt i riktning med pressens skenor F -G cos(45 ^@) =0.
Tyngdkraften som påverkar vikterna och kälken är G =m_(k +p) g, alltså bör motionären påverka kälken med en kraft som minst är av storleken F =m_(k +p) g cos(45 ^@) =160 kg *9,80665 m/s^2 cos(45 ^@) =1109,495795 N ~~1100 N.
Poängsättning:
Det har berättats att kroppen är i jämvikt eller att accelerationen är noll och det har motiverats korrekt med hjälp av Newtons II lag. (2 p.)
En korrekt storhetsekvation för krafternas jämvikt i skenans riktning har presenterats. (2 p.)
Ett korrekt värde för kraftens storlek har givits med två eller tre gällande siffrors noggrannhet. (2 p.)
Typiska fel:
Värdet på cosinus har beräknats med fel enhet för vinkeln.
Cosinusfunktionen förekommer i nämnaren i krafternas jämviktsekvation.
4.3 Motionären lyfter kälken och vikterna genom att räta ut benen. Detta tar 2,8 sekunder. Hur stor är den genomsnittliga effekten av kraften som motionären riktar mot benpressen? Då benen rätas ut rör sig kälken 55 cm längs med skenorna. 6 p.
När motionären rätar ut sina ben utförs på kälken och vikterna arbetet W =F s =1109,495795 N *55 cm =610,2226872 J.
Då det här utförs under en tid av 2,8 sekunder är den genomsnittliga effekten P =W/~Dt =610,2226872 J /2,8 s =217,936674 W ~~220 W.
Poängsättning:
En korrekt storhetsekvation eller värde för arbetet har givits. (2 p.)
En korrekt storhetsekvation för effekten har givits. (2 p.)
Rätt svar har givits med två eller tre gällande siffrors noggrannhet. (2 p.)
5. Vågor 15 p.
Denna uppgift har fem deluppgifter relaterade till vågor. Du kan ändra ditt svar efter att du har valt ett svarsalternativ, men du kan inte längre lämna deluppgiften helt utan svar. Om du har börjat besvara uppgiften men kommer till att du ändå inte vill lämna in den för bedömning, ska du radera ditt svar genom att välja den tomma raden i rullgardinsmenyn och välja alternativet ”Jag svarar inte.” för deluppgifter 5.2–5.5. Rätt svar 3 p., fel svar 0 p. och inget svar 0 p.
5.1 Tryckvariationen för ljud som produceras av två ljudkällor 3 p.
- AC (3 p.)
5.2 Vågor som skapas av två ljudkällor 3 p.
- B (3 p.)
5.3 Vågpulser som reflekteras från en vägg 3 p.
- C (3 p.)
5.4 Ljud och dess spektrum 3 p.
- D (3 p.)
5.5 En våg som fortplantas i en metallfjäder 3 p.
- Våglängden är 6 cm. (3 p.)
6. En kondensators energi 15 p.
6.1 En luftisolerad skivkondensator, vars kapacitans är 0,95\,\mu\rm{F}, är kopplad till en likspänningskälla på 24 V. Gapet mellan kondensatorskivorna fylls med en isoleringsskiva som är gjord av ett material med en relativ permittivitet på 4,5. Hur stor är förändringen i kondensatorns energi när isoleringsskivan läggs till? 5 p.
Kondensatorn vars kapacitans är C =0,95 ~mF, är hela tiden kopplad till spänningskällan, alltså hålls kondensatorns spänning konstant: U = 24 V. Kondensatorns kapacitans är direkt proportionell mot den relativa permittiviteten hos det isolerande materialet mellan kondensatorskivorna. Då luft (relativ permittivitet \approx 1) ersätts med ett isolerande material vars relativa permittivitet är ~e_r =4,5, ökar kondensatorns kapacitans till värdet ~e_r C.
Förändringen i kondensatorns energi är ~DE =E_2 -E_1 =1/2 ~e_r C U^2 1/2 -C U^2 =1/2 (~e_r -1) C U^2 =0,9576 mJ ~~0,96 mJ.
Poängsättning:
Det har berättats att kondensatorns spänning förblir konstant och att kapacitansen ändrar med en faktor \varepsilon_r. (2 p.)
Den korrekta storhetsekvationen för förändringen i kondensatorns energi har givits. (1 p.)
Rätt svar har med två eller tre gällande siffrors noggrannhet givits inom intervallet 0,956 mJ - 0,958 mJ. (2 p.)
6.2 En luftisolerad skivkondensator, vars kapacitans är 1,9 ~mF, kopplas till en likspänningskälla på 12 V. Efter det här kopplas kondensatorn bort från spänningskällan. Kondensatorns skivor flyttas så att avståndet mellan dem blir fyra gånger så stort. Hur stor är förändringen i kondensatorns energi när skivorna flyttas? 6 p.
Laddning bevaras i en kondensator som är isolerad från sin omgivning.
Till en början är kondensatorns kapacitans och spänning C = 1,9 µF och U = 12 V, alltså är dess laddning Q = CU = 22,8 µC. Kondensatorns kapacitans är omvänt proportionell mot avståndet mellan skivorna, alltså kommer en fyrdubbling av avståndet att minska kapacitansens till värdet C/4. Som förändringen i kondensatorns energi får vi ~DE =E_2 -E_1 =Q^2 /(2 C /4) -Q^2 /(2 C) =3 Q^2 /(2 C) =0,4104 mJ ~~0,41 mJ.
Poängsättning:
Det har berättats att kondensatorns laddning bevaras. (2 p.)
Det har berättats att kondensatorns kapacitans minskar till en fjärdedel. (2 p.)
Rätt svar har givits med två eller tre gällande siffrors noggrannhet. (2 p.)
Typiska fel:
Det har antagits att kondensators spänning hålls konstant och som svar har erhållits 0,10 mJ.
6.3 Förklara varför en förflyttning av skivorna i deluppgift 6.2 förändrar kondensatorns energi. 4 p.
Kondensatorskivorna attraherar varandra med elektrostatiska krafter. För att flytta skivorna längre bort från varandra måste de alltså påverkas av krafter riktade utåt. De här krafterna utför ett positivt arbete, vilket lagras som energi i kondensatorns elektriska fält.
Poängsättning:
Ifall det i svaret har berättats
-
att skivorna attraherar varandra, eller
-
att externa krafter utför ett arbete, eller
-
att energi lagras som energi i det elektriska fältet
ges två poäng för varje punkt, tillsammans maximalt (4 p.)
Typiska fel:
Saken förklaras endast med hjälp av förändringen i kapacitansen och möjligtvis med antagandet att spänningen hålls konstant.
7. En magnet i rörelse 15 p.
7.1 Den ena polen av en stavmagnet är svängd mot en kortsluten spole, så som bilden visar. Magneten närmar sig spolen så som det visas i bilden. Varför minskar magnetens rörelseenergi när den närmar sig spolen? 4 p.
Magneten som är i rörelse inducerar en spänning i spolen, varpå en ström uppkommer.
Strömmen i en krets har en viss energi, och den här energin härstammar från magnetens rörelseenergi. För att bevara energin krävs att magnetens rörelseenergi minskar när energi överförs till spolen.
Poängsättning:
Svaret har kopplats korrekt till induktionsfenomenet. (2 p.)
Det har skrivits en konsistent resonemangskedja från induktionsspänning till en minskning av magnetens rörelseenergi. (2 p.)
7.2 Spolen har N ledningsvarv, och dess totala resistans är R. Skriv ett uttryck för den elektriska strömmens effekt i spolen vid tidpunkten då magnetens hastighet är v. Anta att förändringshastigheten för det magnetiska flödet genom spolen är direkt proportionellt mot magnetens hastighet. Du kan beteckna proportionalitetskonstanten med bokstaven k. Hur förändras effekten när spolens resistans ändras? 6 p.
I enlighet med induktionslagen induceras i spolen en spänning U =-N d ~f /(dt) där ~f är det magnetiska flödet genom spolen. Enligt uppgiften är förändringshastigheten i flödet proportionellt mot magnetens hastighet. Vi kan alltså skriva d ~f /dt ~ v eller d ~f /dt =k v där k är en proportionalitetskonstant.
Detta ger spänningen U =-N k v Induktionsspänningen orsakar en elektrisk ström I, och enligt Ohms lag kan vi skriva U =R I Effektförlusten orsakad av den elektriska strömmen är P =U^2/R =(N k v)^2 /R
Av det här uttrycket kan vi se att förlusteffekten ökar om resistansen R minskas.
Poängsättning:
En korrekt storhetsekvation för flödets förändringshastighet har givits med hjälp av k. (2 p.)
En korrekt storhetsekvation för effekten har givits med hjälp av k. (2 p.)
Det har berättats med ord att effekten ökar då resistansen minskar, eller tvärtom. (2 p.)
7.3 Experimentet upprepas, men nu ersätts spolen med ett långt rör som är öppet i båda ändar och gjort av ett ledande material, i vilket magneten placeras. Magnetens massa är 52 g, och dess utgångshastighet är 0,30 m/s. Det finns ingen friktion mellan magneten och röret, och luftmotståndet påverkar inte magneten. Magneten når ändå aldrig andra ändan av röret. Hur mycket energi överförs från magneten till röret under experimentet? 5 p.
Enligt deluppgiften förlorar magneten energi då den rör sig genom det ledande materialet, eftersom en virvelström orsakad av induktionsspänningen induceras i röret. Magnetens hastighet avtar så effektivt att den inte kommer ut ur röret. Därmed har all rörelseenergi överförts till röret genom induktion.
Till en början var magnetens totala rörelseenergi 1/2 *m v^2 =1/2 *0,052 kg *(0,30 m/s)^2 =0,00234 J ~~2,3 mJ
Så här mycket energi överförs från magneten till röret när röret värms upp av virvelströmmarna.
Poängsättning:
Det har motiverats korrekt hur magnetens hela rörelseenergi överförs till röret. (2 p.)
En korrekt storhetsekvation för energin har givits (1 p.) och med hjälp av den har rätt svar beräknats med 2-3 gällande siffrors noggrannhet. (2 p.)
Typiskt fel:
Man har glömt att höja hastigheten till andra potensen och erhållit 7,8 mJ.
8. Dualism och kvantisering av strålning 15 p.
8.1 Elektromagnetisk strålning beter sig som en vågrörelse, alltså förekommer liknande fenomen för elektromagnetisk strålning som för annan vågrörelse. Ge två exempel på experiment eller situationer där ett sådant beteende förekommer. Berätta för vartdera exemplet hur strålningens beteende förklarar det observerade fenomenet eller fenomenen. 6 p.
Som exempel passar experiment där fenomen typiska för elektromagnetisk vågrörelse observeras, somsuperposition eller summering, polarisering eller brytning vid gränsskikt. Fenomenet bör vara sådant som inte observeras med partiklar.
Exempel på experiment:
-
Ljusets diffraktion i en dubbelspalt eller ett gitter: ljus som gått genom olika spalter bildar bakom spaltsystemet ett diffraktionsmönster där ljusvågor som färdats olika sträckor summeras ihop, antingen förstärkande eller försvagande varandra.
-
Interferens i tunna filmer: i ljuset som reflekteras från filmens olika ytor observeras färger som beror på en förstärkning av en del våglängder och försvagning av andra på grund superpositionen av vågor som färdats olika sträckor.
-
Två efterföljande polarisationsfilter: Då det ena filtret roteras märker man att mängden ljus som passerar genom filtren ändras. Ljuset har alltså en egenskap som är kopplad till riktningen vinkelrät mot färdriktningen. Enligt vågmodellen är det fråga om vibrationsriktningen för den elektromagnetiska vågens elektriska fält.
-
Även polarisering vid reflektion, spridning, eller i dubbelbrytande kristaller: Exempelvis vid spridning framkommer vågnaturen genom att inkommande ljus i material får byggstenarna att vibrera i en riktning som är vinkelrät mot rörelseriktningen. Den resulterande spridningsstrålningen är polariserad vinkelrätt mot riktningen för det inkommande ljuset.
-
Ljusets brytning: Exempelvis vid gränsskiktet mellan luft och vatten bryts ljus så att vinkeln mellan ljusstrålen och ytans normal är mindre i vattnet än i luften. Förhållandet mellan sinus av vinklarna är en konstant som är specifik för substansparet. Fenomenet förklaras med ljusets vågnatur då ljusets utbredning modelleras som en vågfront enligt Huygens princip. Alla punkter på vågfronten utgör källor till elementärvågor, vars superposition bildar den nya vågfronten. Från brytningens riktning och vågmodellen kan man förutsäga att ljusets hastighet är lägre i vatten än i luft. Det här har bevisats med mätningar, alltså är vågmodellen giltig för att beskriva brytning.
Poängsättning:För varje korrekta experiment eller situation. (1 p.)
En korrekt förklaring har givits. (2 p.)
Ifall fel eller brister förekommer i förklaringen är avdraget en poäng.
Om fler än två experiment eller situationer har givits bedöms de två sämsta.
Typiskt fel:
Endast fenomenet och inte experimentet har skildrats.
8.2 Elektromagnetisk strålning beter sig som partiklar, alltså påminner strålningens växelverkan med materia som träffar av lokalt eller tidsmässigt åtskilda partiklar. Det här kan observeras direkt, eller så kan en modell som förklarar fenomenet kräva att energi och rörelsemängd överförs från strålningen till materian på samma sätt som vid kollisioner med partiklar. Ge ett exempel på ett experiment eller en situation där ett sådant beteende förekommer. Berätta hur strålningens beteende förklarar det observerade fenomenet eller fenomenen. 3 p.
Exempel:
-
Ett mycket svagt ljus riktas så att det träffar en detektor som kan vara antingen fotografisk film eller en elektronisk anordning, så som ett fotomultiplikatorrör eller en känslig bildsensor. Det svaga ljuset skapar skilda punktformade spår på filmen. Från fotomultiplikatorröret får vi elektriska pulser som motsvarar ”ljuspartiklar”, alltså fotoner, som detektorn detekterar. Med bildsensorn kan man å sin sida observera separationen av växelverkningarna både i plats och tid. Typiskt vill man med den experimentella uppställningen samtidigt också åskådliggöra ljusets vågnatur, varvid det finns en dubbelspalt i vägen för ljuset. Då uppenbarar sig exempelvis på filmen ett diffraktionsmönster som bildas av enskilda punkter.
-
I den fotoelektriska effekten frigör ljus som träffar ett metallstycke elektroner från metallen. Det här kan observeras antingen som en förlust av en negativ laddning som getts till stycket, eller som en elektrisk ström som går från en elektrod till en annan i en fotocell. För att elektroner ska frigöras måste ljusets våglängd vara mindre än ett visst gränsvärde som beror på metallen. Om våglängden är större än gränsvärdet kan inte en ökning av ljusets intensitet få elektronerna att frigöras. En förklaring av fenomenet kräver att ljus växelverkar med metallens elektroner på ett sätt som påminner om kollisioner med partiklar.
-
Vid Comptonspridning märker man i röntgenstrålning som sprids från materia, utöver den ursprungliga våglängden, även en annan större våglängd som avviker mer från den ursprungliga våglängden ju större vinkel strålningen spridits i. En förklaring till det här fenomenet kräver också att strålningen växelverkar med materians elektroner på ett sätt som motsvarar elastiska kollisioner mellan partiklar, där energi och rörelsemängd bevaras.
Poängsättning:
För varje korrekta experiment eller situation. (1 p.)
En korrekt förklaring har givits. (2 p.)
Ifall fel eller brister förekommer i förklaringen är avdraget en poäng.
Om fler än ett experiment eller situation har givits bedöms det sämsta.
Typiskt fel:
Endast fenomenet och inte experimentet har skildrats.
8.3 Energin i elektromagnetisk strålning är kvantiserad, alltså kan energi överföras från strålningen till materia endast i doser vars storlek beror på strålningens frekvens. Ge två exempel på experiment eller situationer där ett sådant beteende förekommer. Berätta för vartdera exemplet hur strålningens beteende förklarar det observerade fenomenet eller fenomenen. 6 p.
Kvantisering av den elektromagnetiska strålningens energi betyder att energi kan överföras mellan strålning och materia endast i doser av vissa storlekar. Detta inkluderar tanken att själva strålningen består av vågpaket, fotoner, vilka har en viss energi. Som exempel lämpar sig experiment där en modell som förklarar de framträdande fenomenen kräver det här.
-
Fotoelektriska effekten: Energi överförs till elektroner i kvantum, vars energi är E =h f. För att frigöra elektroner från en metall behövs en energi som åtminstone är lika stor som det för metallen specifika utträdesarbetet. Om energin för strålningens kvantum är mindre än det här kommer elektroner inte att frigöras, oavsett hur stor intensiteten av strålningen är.
-
Comptonspridning: Även här överförs energi från den inkommande strålningen till elektroner i kvantum, vars energi är E_1 =h f_1. Samtidigt avger elektronen en foton vars energi är E_2 =h f_2. Skillnaden mellan energierna E_1 -E_2 =h (f_1 -f_2) blir kvar hos elektronen. Det att den spridda strålningens energi är beroende av spridningsvinkeln förklaras av en modell där, utöver energins kvantisering, även strålningens rörelsemängd är kvantiserad.
-
Parbildning, där partikel-antipartikelpar uppstår: Som exempel producerar högenergetisk gammastrålning elektron-positronpar. Fenomenet observerades ursprungligen i dimkammare som spår efter partikelparen. Enligt den förklarande modellen omvandlas energin från gammastrålningens foton E =h f enligt lagen E =m c^2 till energin för partikelparets totalmassa. Gammastrålningens frekvens och med den fotonens energi måste vara tillräckligt stora för att fenomenet ska kunna ske.
-
Luminiscens: Fenomenet uppträder exempelvis för en skärm belagd med ett lysämne. Då den belyses med tillräckligt kortvågigt ljus börjar skärmens material emittera ljus. Det inkommande ljuset exciterar lysämnets atomer från lägre tillstånd till högre excitationstillstånd, och lysandet uppstår när excitationstillstånden återgår till lägre tillstånd. För att excitera atomerna från ett tillstånd till ett annat krävs ett energikvantum som är lika stort som skillnaden mellan tillstånden. Om det inkommande ljuset inte innehåller tillräckligt många kortvågiga fotoner sker ingen excitation och luminiscens kan inte observeras.
-
Spektrum: Ett experiment där ett absorptions- eller emissionsspektrum mäts, om examinanden har lyckats koppla förklaringen till fotoner.
Poängsättning:
För varje korrekta experiment eller situation. (1 p.)
En korrekt förklaring har givits. (2 p.)
Ifall fel eller brister förekommer i förklaringen är avdraget en poäng.
Om fler än två experiment eller situationer har givits bedöms de två sämsta.
Typiskt fel:
Endast fenomenet och inte experimentet har skildrats.
Del 3: 20-poängsuppgifter
9. En fisks simblåsa 20 p.
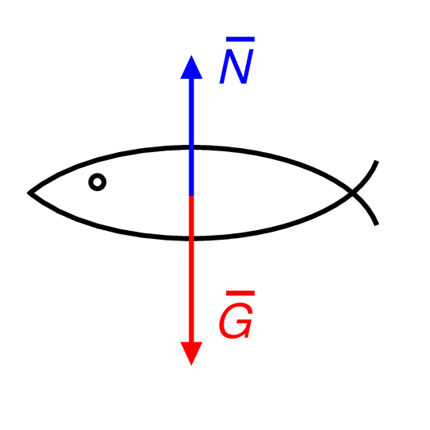
Många fiskarter kan reglera sitt simdjup med hjälp av en så kallad simblåsa. Simblåsan (bild ) är ett organ som finns i övre delen av kroppshålan, och den innehåller luft. Simblåsan har flexibla väggar som drar ihop sig och expanderar under påverkan av det omgivande trycket. Vid olika djup råder olika vattentryck vilket påverkar fiskens inre tryck, varvid även simblåsans volym förändras. Fiskens totala volym förändras lika mycket som simblåsans volym, vilket resulterar i en förändring av den lyftkraft som påverkar fisken. Fisken kan dock påverka simblåsans volym: med hjälp av gaskörtlar kan fisken utsöndra luft som lösts i blodet till blåsan eller tvärtom minska luftmängden i blåsan och därmed ändra simblåsans och hela fiskens volym.
I följande deluppgifter undersöker vi en fisk vars simblåsa har en volym på 0,079 dm^3 och den totala kroppsvolymen 0,623 dm^3 när fisken befinner sig strax under havsytan. Lufttrycket vid ytan är 101,3 kPa, och luftens molmassa är 29,0 g/mol. Vattnets temperatur vid ytan är 17,7 ^@ C, och vattnets densitet förblir nästan oförändrad 1,0 kg/dm^3 oberoende av djupet och temperaturen.
9.1 En fisk som flyter i jämvikt strax under havsytan blir skrämd och simmar snabbt till ett djup på 7,6 meter där den tillfälligt stannar. Fisken är inte i jämvikt eftersom luftmängden i simblåsan och fiskens temperatur inte har hunnit förändras under den snabba simfärden. Rita kraftfiguren för fisken som tillfälligt stannat vid ett djup på 7,6 meter och bestäm storleken och riktningen på den totala kraften som påverkar fisken. 8 p.
Fisken påverkas av tyngdkraft och en lyftkraft, alltså är den totala kraften sum vec F = vec G +vec N, där krafternas riktningar är motsatta. Den positiva riktningen bestäms som nedåt, varvid F =G -N. Som kraftfigur får vi följande:
Den totala kraften strax under havsytan är F_0 =G -N =0 --> m g -~r V_0 g =0 , alltså är m g =~r V_0 g där V_0 är fiskens totala volym och m är fiskens massa.
Vid dykning ändras det yttre trycket och fiskens volym, varvid den totala kraften är F_1 =m g -~r V_1 g =~r V_0 g -~r (V_0 -~DV) g=~r ~DV g, där ~DV är förändringen i fiskens totala volym.
Vid normaltillstånd beter sig luft som en ideal gas, alltså kan vi använda tillståndsekvationen för en ideal gas för att bestämma förändringen i volymen. Temperaturen och substansmängden förblir konstanta vi förändringen, varvid pV\ = konstant. Därmed är p_0 V'_0 =p_1 V'_1 , alltså V'_1 =V'_0 p_0/p_1, där p är det yttre trycket och V' är simblåsans volym vid de olika situationerna. Förändringen i fiskens volym är lika stor som förändringen i simblåsans volym, alltså ~DV =V'_0 -V'_0 p_0/p_1.
Det yttre trycket strax under ytan, p_0 är lika stort som lufttrycket, medan det hydrostatiska trycket, ~r g h_1, måste läggas till det totala trycket vid 7,6 meters djup, varvid vi som volymens förändring får ~DV =V'_0 (1 -p_0/(p_0 +~r g h_1)).
För den totala kraften vid 7,6 meters djup får vi F_1=\rho g V_0'\Bigl(1-\frac{p_0}{p_0+\rho gh_1}\Bigr) =1,\!00\,\frac{\rm kg}{\rm{dm}^3}\cdot 9,\!81\,\frac{\rm m}{\rm{s}^2}\cdot0,\!079\,\rm{dm}^3\Bigl(1-\frac{101300\,\rm{Pa}}{101300\,\rm{Pa}+1000\,\frac{\rm kg}{\rm{m}^3}\cdot 9,81\,\frac{\rm m}{\rm{s}^2}\cdot 7,6\,\rm{m}}\Bigr) =0,\!32856515808\,\rm{N}\approx 0,\!33\,\rm{N}.
Den totala kraften är 0,33 N, och den är riktad nedåt.
(Vid jämviktsläget strax under havsytan påverkades fisken av en lyftkraft som var N =~r V_0 g ~~6,11 N, alltså är lyftkraften i den nya situationen ungefär 0,3286 N/6,112 N ~~5 % mindre är fiskens tyngd.)
Poängsättning:
En korrekt ritad kraftfigur där lyftkraften och tyngden namngivits med ord eller symboler. (2 p.)
Följande poängavdrag görs från kraftfiguren:
-
För grova fel (saknade krafter, överlopps krafter eller krafter som verkar i fel riktning) är avdraget två poäng.
-
För betydande fel (kraftens namn eller symbol saknas) är avdraget en poäng.
En storhetsekvation för den totala kraften vid 7,6 m djup har skrivits med hjälp av tyngden och lyftkraften. (2 p.)
En storhetsekvation för förändringen i fiskens volym har skrivits med hjälp av trycket eller korrekt värde för förändringen i volymen har beräknats. (2 p.)
Det har givits rätt storlek för kraften med 2-3 gällande siffrors noggrannhet (1 p.) och rätt riktning för kraften. (1 p.)
9.2 Efter det här blir fisken kvar på ett djup på 7,6 meter, där temperaturen är 11,3 ^@C Fiskens kroppstemperatur utjämnas till omgivningens temperatur. Utöver trycket påverkar också temperaturförändringen volymen av luften i simblåsan. Hur mycket mer luft behöver fisken utsöndra till simblåsan för att flyta i jämvikt på ett konstant djup av 7,6 meter? Ange svaret i milligram. 6 p.
Med hjälp av tillståndsekvationen för en ideal gas, p V =n R T, kan vi lösa massan av den extra luft som behövs i en situation där den kallare luften inuti simblåsan påverkas av ett större tryck. Den ursprungliga substansmängden för luften i simblåsan var n_0 =(p_0 V'_0) /(R T_0) och substansmängden som behövs för att vara i jämvikt är n_1 =(p_1 V'_1) /(R T_1), varvid substansmängden för den extra luften är ~Dn =n_1 -n_0 =(p_1 V'_1) /(R T_1) - (p_0 V'_0) /(R T_0)
Fisken flyter åter i jämvikt då simblåsans volym är samma som den var strax under havsytan, alltså är V'_0 =V'_1, och vi får ~Dn =V'_0 /R (p_1/T_1 -p_0/T_0) =V'_0/R ((p_0 +~r g h_1) /T_1 -p_0/T_0).
Massan av den extra luften är ~Dm =~Dn *M ==M V'_0/R ((p_0 +~r g h_1) /T_1 -p_0/T_0), där M =29,0 g/mol är luftens molmassa, V'_0 =0,079 dm^3 =0,000079 m^3 är simblåsans ursprungliga volym, T_1 =273,15 K +11,3 K =284,45 K är temperaturen vid 7,6 meters djup, T_0 =273,15 K +17,7 K =290,85 K är temperaturen vid ytan och h_1 =7,6 m är djupet som fisken är på under havsytan.
Vi får ~Dm =0,07438507719 g ~~74 mg.
Poängsättning:
Det har konstaterats med ord eller det framgår ur beräkningarna att fiskens volym ska vara lika stor som då den flöt i jämvikt strax under havsytan. (2 p.)
En storhetsekvation för förändringen i massan har skrivits med hjälp av trycket och volymen. (2 p.)
Rätt svar för förändringen i massan har givits med 2-3 gällande siffrors noggrannhet inom intervallet 74 mg - 75 mg. (2 p.)
Typiskt fel:
Förändringen i massan har beräknats utan att beakta temperaturförändringen och som svar har man fått ~Dm =0,07222569516 g ~~72 mg.
9.3
Vid ekolodning reflekteras ljudvågor som skickats ut i vattnet från fiskarna (bild ). Även små fiskar kan tydligt observeras om ljudvågorna resonerar med luften som finns i fiskarnas simblåsor. En sådan simblåsa i resonans kan förenklat ses som ett rör som är slutet i båda ändar.
En fisk syntes tydligt med ekolod när ljudets frekvens var minst 2,4 kHz. Beräkna längden på den största kaviteten i fiskens simblåsa och fiskens avstånd från ekolodet då ljudet som reflekteras från fisken återvände 12 ms efter att det skickats i väg. Ljudets hastighet i luft är 343 m/s och i vatten 1 484 m/s.
6 p.
Resonans uppträder då en stående våg uppstår i simblåsan. I båda änder av ett slutet rör bör då finnas noder, alltså kan våglängden för ett ljud som skapar resonans som störst vara ~l =2 l.
Med hjälp av vågekvationen, v =~l f, kan vi uttrycka rörets längd som funktion av frekvensen l =1/2 ~l =v /(2 f).
Ljudets hastighet i simblåsan är v =343 m/s och frekvensen, f =2,4 kHz, förblir densamma oavsett medium. För simblåsans längd får vi l =343 m/s /(2 *224 kHz) =0,071458333 m ~~7,1 cm.
Fiskens avstånd från ekolodet är hälften av avståndet som ljudvågen färdats x =1/2 s =1/2 v t, där v =1484 m/s är ljudets hastighet i vatten. Som avstånd får vi x =1/2 *1484 m/s *12 ms ~~8,9 m.
Poängsättning:
Det har konstaterats med ord eller berättats med en bild att en stående våg uppstår i simblåsan, eller att vågen i simblåsan har en nod i vardera ända. (2 p.)
Rätt svar för simblåsans längd har givits med 2-3 gällande siffrors noggrannhet inom intervallet 7,14 cm – 7,15 cm. (2 p.)
Rätt svar för fiskens avstånd har givits med 2-3 gällande siffrors noggrannhet inom intervallet 8,59 m – 8,91 m. (2 p.)
Typiska fel:
-
Ljudets våglängd har givits som längden av simblåsan.
-
Fiskens avstånd har tänkts vara hela sträckan tur och retur.
-
Avståndet har beräknats så att ljudet färdas i simblåsan under en del av tiden, vilket resulterar i ett något kortare avstånd. Dessa avstånd ligger dock inom gränserna för ett godkänt svar.
10. En kabelskyddsbrytare 20 p.
10.1 Defekta elektriska apparater som är anslutna till elnätet kan orsaka elolyckor och andra skador i hemmet. Varför är en elektrisk stöt farlig för människor? Vilka andra olyckor kan en defekt elektrisk apparat orsaka i hemmet? 4 p.
En defekt apparat som är kopplad till elnätet kan orsaka en elstöt, varvid människan blir en del av strömkretsen och den elektriska strömmen går genom hen. Den elektriska strömmen kan störa nervsystemets funktion hos människan eller orsaka en brännskada. En defekt apparat kan också överhettas och orsaka brand i hemmet.
Poängsättning:
Den elektriska strömmens effekt på hjärtat eller nervsystemet har omnämnts eller så har kramper eller brännskador omnämnts. (2 p.)
Det har nämnts att en apparat kan orsaka brand. (2 p.)
Typiska fel:
Det har påståtts att en elektrisk stöt kan orsaka en hjärtattack.
10.2 I utlösningskurvan för en kabelskyddsbrytare (bild ) kan man skilja mellan två områden, de så kallade termiska (T) och magnetiska (M) områdena. Mot vilka typer av strömkretsfel garderar man sig med de här områdena i utlösningskurvan? 6 p.
I det termiska området är den elektriska strömmen bara några gånger större än brytarens märkström. Om de pågår för länge leder sådana här fall till att kretsen överhettas och slutligen till en brand. Med det termiska området förbereder man sig alltså för en situation där någon apparat i strömkretsen använder en elektrisk ström som är större än märkströmmen under en lång tid.
I det magnetiska området är de elektriska strömmarna mycket större än brytarens märkström och den elektriska strömmen bryts mycket snabbt. Med det magnetiska området förbereder man sig alltså för situationer där en mycket stor elektrisk ström plötsligt skapas i kretsen, alltså exempelvis för kortslutningar.
Poängsättning:
Det har identifierats att man med det termiska området förbereder sig för ett fel där den elektriska strömmen är en aning större än märkströmmen (1 p.) och det har berättats att ett sådant fel orsakar problem om det fortgår under en lång tid. (2 p.)
Det har identifierats att man med det magnetiska området förbereder sig för ett fel där den elektriska strömmen är betydligt större än märkströmmen (1 p.) och det har berättats att brytningen då bör ske snabbt eller att man med det här förbereder sig för en kortslutning. (2 p.)
Ifall den elektriska strömmens storlek inte behandlats korrekt kan en identifiering av vartdera felets längd ge en poäng.
Typiska fel:
-
Det har påståtts att brytningen mäter temperatur i det termiska området och magnetiska fältet i det magnetiska området.
-
Det blandas mellan brott i ledarna och kortslutning.
-
Svaret kopplas inte till fel i strömkretsar.
10.3 I en elnätskrets är kabelskyddsbrytarens märkström 16 A. En apparat som är ansluten till kretsen får ett fel och en elektrisk ström på 32 A uppstår i strömkretsen. Hur mycket elektrisk energi hinner överföras till apparaten innan den elektriska strömmen bryts? 6 p.
Den elektriska energins effekt är P =U I, så storleken på energin som överförs till apparaten är E =P t =U I t, där vi avläst från kabelskyddsbrytarens utlösningskurva får 10 <= t <= 45 s.
Energi överförs som minst E_1 =U I t_1 =230 V *32 A *10 s =73.600 J ~~74.000 J.
Energi överförs som mest E_2 =U I t_2 =230 V *32 A *45 s =331.210 J ~~330.000 J.
Poängsättning:
Ett korrekt värde för tiden motsvarande övre eller nedre gränsen har avläst från grafen (2 p.) och utgående från det har ett värde erhållits för energin inom intervallet 70 kJ - 384 kJ. (2 p.)
Det har korrekt beräknats med 1 - 3 gällande siffrors noggrannhet ett värde för både övre gränsen inom intervallet 290 kJ - 384 kJ och nedre gränsen inom intervallet 70 kJ - 80 kJ. (2 p.)
Typiska fel:
Värdet för den överförda laddningen har beräknats.
10.4 Kabelskyddsbrytaren kan endast upptäcka situationer där strömmen i kretsen blir för stor. Det kan dock förekomma andra fel i en elnätskrets som orsakar faror eller problem i kretsens funktion om man inte skyddar sig mot dem. Vilka andra fel som kräver skyddsåtgärder kan det förekomma i en elnätskrets? Nämn åtminstone två. 4 p.
Kabelskyddsbrytaren missar en del av kretsens felsituationer. Exempel på de här situationerna:
-
De inmatade och de utgående elektriska strömmarna är inte lika stora. Den saknade delen av den elektriska strömmen kallas läckström och det krävs en separat anordning, en jordfelsbrytare, för att detektera den.
-
Spänningen och strömmen i kretsen är inte i samma fas. Då går det en reaktiv ström i kretsen, vilket kabelskyddsbrytaren inte kan detektera.
-
En fas ur trefasström faller till noll.
-
Det finns små störningar i spänningens kvalitet, till exempel brus eller andra kortvariga avvikelser från den sinusformade spänningen. Eftersom kabelskyddsbrytaren endast övervakar storleken på den elektriska strömmen kan den inte upptäcka sådana störningar.
Poängsättning:
För varje korrekta fel eller situation. (2 p.) De två bästa bedöms.
Typiska fel:
Det påstås att ett brott i strömmen eller att en apparat går sönder är ett fel.
Det påstås att få en elstöt är ett fel. Det kan vara en följd av ett fel.
Det påstås att en kortslutning, för vilket kabelskyddsbrytaren skyddar, är ett fel.
11. Supraledning 20 p.
11.1 Varför stiger magneten upp i luften? Varför kan fenomenet inte förklaras med hjälp av induktionslagen? 5 p.
Enligt induktionslagen uppstår en induktionsspänning i en slinga då det magnetiska flödet genom slingan ändras som funktion av tiden. I situationen som visas i videon är magneten till en början stillastående på skivan som blir supraledande. Det magnetiska flödet genom skivan är alltså konstant och förändringen i det magnetiska flödet per tidsenhet är noll. Virvelströmmarna som bildas på ytan av supraledaren kan därmed inte förklaras med hjälp av klassisk elektromagnetisk induktion.
Då skivan kyls ner blir den supraledande. Till supraledarens grundegenskaper hör att ledaren stänger ut det yttre magnetfältet med det motsatta magnetfältet som virvelströmmarna på ytan orsakar. Magnetfält som är motsatt riktade repellerar varandra, så magneten stiger upp i luften. Eftersom supraledaren stänger ut det yttre magnetfältet ändrar det magnetiska flödet genom det supraledande stycket, men det ändrar först efter att virvelströmmarna har uppkommit.
Poängsättning:
Det har motiverats att induktionslagen inte förklarar fenomenet med det att magneten inte rör på sig. (2 p.)
Det har berättats att det yttre magnetfältet orsakar virvelströmmar i supraledaren och att de här virvelströmmarna skapar ett magnetiskt fält. (2 p.)
Det att magneten stiger upp i luften har motiverats antingen med en repellerande magnetisk kraft, magnetiska poler som repellerar varandra eller genom att berätta att kraften som uppstår är lika stor som skivans tyngd. (1 p.)
11.2 Vad händer om den svävande magnetens nordpol vänds mot supraledaren? Fortsätter magneten sväva eller faller den ner på ytan av supraledaren? 4 p.
Enligt materialet stöter en supraledare alltid bort externa magnetfält genom att bilda virvelströmmar på sin yta. Det här sker oavsett om magnetens nordpol eller sydpol är riktad mot supraledaren. Om magneten svängs åt andra hållet svänger även riktningen på virvelströmmarna på supraledarens yta, varvid den repellerande kraften mellan supraledaren och magneten hålls konstant och magneten fortsätter sväva.
Poängsättning:
Det har svarats att magneten fortsätter sväva. (1 p.)
Rätt svar har motiverats genom att berätta att virvelströmmarnas riktning ändrar till det motsatta. (3 p.)
11.3 Vilka fördelar skulle uppnås om supraledning kunde åstadkommas i rumstemperatur? 4 p.
Vid elöverföring finns det alltid en motståndsförlust på några procent. Om man kunde använda supraledare skulle elektricitet kunna överföras utan energiförluster, vilket årligen skulle spara mycket pengar. Kablarna kunde vara rätt tunna eftersom deras elektriska motstånd är noll.
Effektförluster från de elektriska strömmarna värmer upp komponenter i alla elektroniska apparater. Det här kan leda till överhettning. Därför har det ofta tillsatts lufthål och kylflänsar. Om ledarna var supraledande skulle lufthål och flänsar inte behövas. Apparaterna skulle kunna vara mindre och komponenterna installeras närmare varandra på kretskorten.
Poängsättning:
Mindre energi- eller effektförluster vid energiöverföring har identifierats. (2 p.)
Med hjälp av det föregående har en rimlig fördel motiverats, exempelvis förminskning av apparaterna, kostnaderna eller nedkylningsbehoven eller möjligheten att använda tunnare eller längre ledare. (2 p.)
Typiska fel:
-
Förlusterna förklaras utan att koppla dem till energi.
-
Endast tillämpningar erbjuds som fördelar.
-
Fantasianordningar erbjuds.
11.4 Vilka problem relaterade till materialet har högtemperatursupraledare? Kan en tunn supraledande tråd bära en hur stor ström som helst? 4 p.
Eftersom materialen är keramiska är det svårt att göra kablar av dem. Kablarna måste tåla mekanisk påfrestning utan att gå av, vilket keramiska material sällan klarar av. (Exempelvis är den supraledande skivan i videon full av sprickor.)
En supraledande kabels kritiska strömtäthet får inte heller överskridas. Den kritiska strömtätheten multiplicerad med kabelns tvärsnittsyta bestämmer den största möjliga ström som kan gå genom kabeln, alltså måste kabeln ha en viss minimitjocklek om den ska kunna bära stora strömmar. Om strömtätheten överskrids värms kabeln upp och den övergår till normalt tillstånd, vilket kan leda till att den smälter.
Poängsättning:
Det har identifierats att materialet eller ledare gjorda av materialet har en tendens att gå sönder genom att använda något annat ord än det "skör" som givits i materialet. (2 p.)
Den senare frågan har besvarats med ett "nej" och motiverats med att koppla samman strömmen genom kabeln, den kritiska strömtätheten och kabelns tvärsnittsyta. (2 p.)
Typiskt fel:
Att texten helt enkelt kopierats från materialet.
11.5 Varför används supraledare av typ II i supraledande magneter? 3 p.
Det kraftiga magnetfältet från en supraledande spole påverkar även den supraledande tråden i själva spolen. Enligt materialet är värdet på Bc litet för typ I supraledare. Om det överskrids i spolen övergår tråden plötsligt till normalt tillstånd och strömmen som går i ledaren kan skada tråden. I fallet med en typ II supraledare förblir ledningstråden supraledande så länge som den magnetiska flödestätheten inte överskrider värdet Bc2 inuti spolen. Enligt materialet är värdet på Bc2 stort för typ II supraledare. Typ II supraledare är därför säkrare att använda i spolar än ledare av typ I.
Poängsättning:
En eller båda av följande har identifierats korrekt (3 p.)
-
spolens egna magnetiska fält påverkar spolen och orsakar ett fält vars styrka inte får överskrida det kritiska fältet
-
typ II supraledare tål större magnetiska fält än vad typ I supraledare gör.
Ifall ingendera har identifierats, men det har berättats korrekta saker tagna ur materialet om beteendet för typ II supraledare i ett magnetiskt fält, ges en poäng.