Hyvän vastauksen piirteet: FI – Matematiikka, pitkä oppimäärä

1.

Kulmakerroin on \frac35 ja perustelu laskulla \frac{0-(-3)}{5-0}=\frac{3}{5} tai selkeällä kuvalla. (1+1 p.)

Suoran yhtälö on y=\frac{3}{5}x-3 ja vakiotermin perustelu, esimerkiksi pisteen (0,-3) avulla. (1+1 p.)

TAI

Suoran yhtälö on muotoa y=kx-3, ja perustelu: kulkee pisteen (0,-3) kautta tai käytetty muotoa y-(-3)=k(x-0). (1+1 p.)

Suoran yhtälö on y=\frac{3}{5}x-3 ja perustelu: sijoitetaan yhtälöön toinen piste (5,0), jolloin saadaan 0=5k-3, eli k=\frac{3}{5}. (1+1 p.)

Tähän osatehtävään liittyvät erillisohjeet

Pelkkä vastaus (1+0)+(1+0) (2 p.)

Vastaus voi olla normaalimuodossa, esimerkiksi -3x+5y+15=0.

Merkkivirhe kulmakertoimessa, koordinaatit väärässä järjestyksessä tms. (max 3 p.)

Koordinaatit väärinpäin (saatu x=\frac{3}{5}y-3 tai -3y+5x+15=0). (max 3 p.)

2.

f'(x) =6 x +4 e^(4 x) (Ensimmäinen termi 2 p. Jälkimmäisessä sisäfunktion ja ulkofunktion oikeasta derivaatasta saa kummastakin yhden pisteen. Ylimääräisistä termeistä vähennetään 1 piste.) (4 p.)

Tähän osatehtävään liittyvät erillisohjeet

Pelkkä oikea vastaus. (4 p.)

Ylimääräisiä tekijöitä (esimerkiksi 4xe^{4x}) (max 3 p.)

3.

int cos(5 x) dx =1/5 sin(5 x) +C, (Kerroin 1/5 + sin(5 x) + oikein integrointivakiota lukuunottamatta + C.) (4 p.)

Tähän osatehtävään liittyvät erillisohjeet

Pelkkä oikea vastaus. (4 p.)

Integroitu aivan väärin, mutta on +C. (1 p.)

1.

Kerrotaan sulut auki ja saadaan vasen puoli x^2 +2 x -3 tai vastaava muoto, josta epäyhtälö muotoon x^2 +2 x > 0. (2 p.)

Ratkaistaan nollakohdat: x^2 +2 x =0, eli x (x +2) =0, josta x =0 tai x =-2. (2 p.)

Kyseessä on ylöspäin aukeava paraabeli, joten epäyhtälön ratkaisu on x < -2 tai x > 0. (2 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Jos käsitellään vain epäyhtälöitä, niin 0 p. riviltä 2, max 2+0+2 esimerkiksi perustelulla ''koska x(x+2) on ylöspäin aukeava paraabeli, ratkaisu on x<-2 tai x > 0''.

Rivin 3 perustelu voidaan tehdä myös testipisteillä.

Riviltä 3 vain perustelupiste, jos rivillä 2 väärä polynomi tai nollakohta. 2+0+1 (max 3 p.)

Epäyhtälöstä x(x+2) > 0 suoraan oikea vastaus x<-2 tai x > 0 ilman perustelua. (2+0+1 p.)

TAI

Kerrotaan sulut auki ja saadaan vasen puoli x^2+2x-3 tai vastaava muoto, josta epäyhtälö muotoon x^2+2x>0. (2 p.)

Tekijöiden merkit kaaviossa tai sanallisesti, (2 p.)

tulon merkeistä päätellään, että epäyhtälön ratkaisu on x<-2 tai x>0. (2 p.)

2.

Löydetty ratkaisut x=-e, x=\pi ja x=-\pi. (3 p.)

Perusteltu tulon nollasäännöllä (3 p.) TAI tarkistus (1 p.) + kolmannen asteen polynomilla on korkeintaan kolme juurta (2 p.). (1+2 p.)

Tähän osatehtävään liittyvät erillisohjeet

Pisteet tulon nollasäännöstä, jos sen käyttö mainitaan tai kirjoitetaan vastaavat yhtälöt. (2 p.)

Mikäli perusteluna vain tekijöihinjako (x+e)(x-\pi)(x+\pi) ilman mainintaa tulon nollasäännöstä tai yhtälöitä. (max 3+1 = 4 p.)

Likiarvoja vastauksessa. (-1 p.)

Tietoa (\sin x)^2 +(\cos x)^2 =1 on yritetty käyttää + sijoitus oikein. (1+1 p.)

Tietoa \sin (2x)=2\sin (x)\cos (x) on yritetty käyttää + sijoitus oikein. (1+1 p.)

STOP Jatkosta pisteitä vain jos rivi 1 tai rivi 2 on oikein.

Otettu (\sin x)^2 yhteiseksi tekijäksi ja saatu yhtälö (\sin x)^2(1-4(\cos x)^2)=0 TAI poistettu neliö oikein ja saatu yhtälö \sin(x) = \pm 2 \sin(x)\cos(x). (1 p.)

Jatkettu tulon nollasäännöllä. (Piste vaatii, että edelliseltä riviltä on saatu 1 p.) (1 p.)

Saatu (ilman perustelua) yhtälöstä \sin x=0 ratkaisut melko täsmälleen x=0 ja melko täsmälleen x=\pm \pi. (1+1 p.)

Yhtälöstä \cos x=\pm \frac{1}{2} saatu esimerkiksi yleisen ratkaisun tai muiden perustelujen avulla melko täsmälleen x=\pm \frac{\pi}{3} ja melko täsmälleen x=\pm \frac{2\pi}{3}. (Perustelut 2 p. + ratkaisut: puolet 1 p. + loput 1 p.) (2+2 p.)

TAI

Tietoa (\sin x)^2 = 1-(\cos x)^2 on yritetty käyttää + sijoitus oikein. (1+1 p.)

STOP Jatkosta pisteitä vain jos rivi 1 on oikein.

Saatu yhtälö (\sin x)^2 = (\sin(2x))^2.

Neliö poistettu oikein ja saatu yhtälöt \sin(x) = \pm \sin(2x). (1+1 p.)

Saatu (ilman perustelua) yhtälöstä \sin x = \sin(2x) ratkaisu melko täsmälleen x=0. (1 p.)

Ratkaistu yhtälö \sin x = \sin(2x), saatu ratkaisut melko täsmälleen x=\pm \pi, melko täsmälleen x=\pm \frac{\pi}{3}. (x=2x+2\pi k (1 p.), x=2\pi k+\pi-2x (1 p.), ratkaisut: puolet (1 p.) + loput (1 p.)) (2+2 p.)

Ratkaistu yhtälö \sin x = -\sin(2x), saatu ratkaisut melko täsmälleen x=\pm \frac{2\pi}{3} (2 p.) JA melko täsmälleen x=0 ja melko täsmälleen x= \pm \pi (1 p.). (3 p.)

TAI

Muutettu (\cos x)^2 järkevään muotoon, esim. \cos^2(x) = \frac12 (1+\cos(2x)), ja sijoitettu tieto yhtälöön. (1+1 p.)

Muutettu (\sin(2x))^2 järkevään muotoon, esim. \sin^2(2x) = \frac12 (1-\cos(4x)), ja sijoitettu tieto yhtälöön. (1+1 p.)

STOP Jatkosta pisteitä vain jos rivi 1 tai rivi 2 on oikein.

Saatu (ilman perustelua) yhtälöstä melko täsmälleen x=0. (1 p.)

Ratkaistu (2 p.) saadusta yhtälöstä melko täsmälleen x=\pm \pi, melko täsmälleen x=\pm \frac{\pi}{3}. (2 p.) (2+2 p.)

Ratkaistu yhtälöstä melko täsmälleen x=\pm \frac{2\pi}{3}. (3 p.)

Tähän tehtävään liittyvät erillisohjeet

2. ja 3. arvosteluohjeen kahden viimeisen rivin vastauspisteet edellyttävät perustellusti saatuja ratkaisuja.

Alkupiste (1 p.): Yksi tai kaikki ratkaisut arvattu ja testattu.

Mukana juuri, joka ei ole ko. yhtälön ratkaisu. Vähennys -1 p./kpl siltä riviltä, jolla virhe on tehty.

Ratkaisujen rajoittamista ei tarvitse perustella, vaan riittää löytää oikeat arvot. Jos on ratkaisut rajoittamatta, esimerkiksi \pi +k2\pi tai rajausehtoa x\in [-\pi,\pi] käytetty väärin: -1 piste per rivi, jolla virhe on tehty. Koskee kahta viimeistä riviä.

Tehty asteissa oikein, ja saatu -180,-120,-60, 0, 60,120 ja 180 astetta. (max 12 p.)

Yhtälön ratkaisemiseksi ei kelpaa nollakohdan arvaaminen ja testaaminen.

1.

Alkuperäinen keskiarvo jossakin muodossa, esimerkiksi a = \frac{x_1 + \dots +x_n}{n} tai x_1 + \dots +x_n = an. (1 p.)

Uusi keskiarvo jossakin muodossa, esimerkiksi \frac{x_1 + \dots +x_n +b}{n+1}. (1 p.)

Verrattu keskiarvoja järkevällä tavalla, esimerkiksi erotus tai osamäärä tai muodostettu epäyhtälö ''alkuperäinen ka'' < ''uusi ka''. (1 p.)

Järkevä muokkausaskel, esimerkiksi nimittäjät kerrottu pois tai lavennettu saman nimisiksi. (1 p.)

Muokattu sopivaan muotoon ja käytetty tietoa a<b. (1+1 p.)

TAI

Alkuperäinen keskiarvo ei muutu, kun lisätään a, JA perustelu tälle. (1+2 p.)

a:ta suuremman luvun b lisääminen kasvattaa keskiarvoa JA perustelu tälle. (2+1 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Lukujen n tai n+1 positiivisuutta ei tarvitse mainita.

Esimerkki ratkaisusta: \frac{x_1+x_2+\cdots +x_n+b}{n+1} =\frac{na+b}{n+1} >\frac{na+a}{n+1}=a.

Tähän osatehtävään liittyvät erillisohjeet

Väite \Rightarrow \dots \Rightarrow a<b. (-0 p.)

2.

Annettu toimiva esimerkki. (2 p.)

Annettu esimerkki, jossa vähintään kolme eri lukua:

riippumaton Esimerkissä osoitettu, että moodi on 1. (1 p.)

riippumaton Esimerkissä osoitettu, että mediaani on 100. (1 p.)

riippumaton Esimerkissä osoitettu, että keskiarvo on 10. (2 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Jos keskiarvo \ne 10, mutta likiarvo laskettu oikein ja välillä [9{,}5;10{,}5[, niin viimeiseltä riviltä 1 p.

Annettu useampi eri esimerkki. Pisteet vain yhdeltä yllä olevista riippumaton-riveistä. (max 2 p.)

TAI (Rakennetaan esimerkki: riviltä pisteet vain jos riviä vastaava ominaisuus näkyy ANNETUSSA (mahdollisesti puutteellisessa) esimerkissä)

Konstruktiossa idea, miten moodiksi saadaan 1. (1 p.)

riippumaton Konstruktiossa idea, miten mediaaniksi saadaan 100. (1 p.)

riippumaton Konstruktiossa idea, miten keskiarvoksi saadaan 10 (1 p.)

Viety konstruktio loppuun, esimerkiksi ratkaistu vapaa muuttuja (1 p.)

Annettu toimiva esimerkki kuten -338, 1, 1, 100, 101, 102, 103. (2 p.)

Ratkaistaan y tai x ympyrän yhtälöstä: y=\pm \sqrt{4-x^2} tai x=\pm \sqrt{4-y^2}. (2 p.)

riippumaton Huomattu, että x\in [-2,2] TAI y\in [-2,2]. (1 p.)

Sijoitetaan lausekkeeseen tapaus y=+\sqrt{4-x^2} : f(x,\sqrt{4-x^2})=x\sqrt{4-x^2}. (1 p.)

Ajatus derivoinnista + derivoitu oikein:
D(x\sqrt{4-x^2})=\sqrt{4-x^2}+\frac{x\cdot (-2x)}{2\sqrt{4-x^2}}\ (=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}) (kun -2<x<2). (1+1 p.)

Nyt \sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}=\frac{4-2x^2}{\sqrt{4-x^2}}=0, kun x=\pm \sqrt{2}. (1 p.)

Lasketaan arvot derivaatan nollakohdassa ja päätepisteissä TAI kulkukaavio: f(2,0)=0, f(-2,0)=0 ja f(\sqrt{2},\sqrt{2})=2, f(-\sqrt{2},\sqrt{2})=-2. (2 p.)

Lausekkeen pienin arvo tässä puolikkaassa on -2 ja suurin on 2, joten (jatkuvuuden nojalla) f saa arvot [-2,2]. (1+1 p.)

Mainittu, että tapaus x= -\sqrt{4-y^2} tai y= - \sqrt{4-x^2} on symmetrinen ja f saa samat arvot. (1 p.)

Tähän ratkaisuun liittyvät erillisohjeet

\pm puuttuu rivillä 1 eikä symmetriaa käsitelty muuten (1+1+1+2+1+2+2+0) (max 10 p.)

Rivillä 1 muu virhe kuin puuttuva \pm (poistettu juuri väärin tms.), derivoinnista vain ideapiste. (0+1+1+(1+0)+1+2+(0+0)+1) (max 7 p.)

Laskettu vain f(-2,0) tai f(2,0) (+0 p.)

TAI

Ympyrän säde on 2 ja se on origokeskeinen. [1+1 p.]

Ympyrän parametrimuotoinen yhtälö on \begin{cases} x=2\cos t \\ y=2\sin t, \end{cases} (missä t\in[0,2\pi].) (2 p.)

Sijoitettu x ja y funktion f yhtälöön, saatu f(t)=2\cos t\cdot 2 \sin t=4\cos t \sin t (2 p.)

=2\sin (2t) (2 p.)

(Välillä t\in [0,2\pi]) funktio \sin (2t) saa arvot [-1,1], (2 p.)

joten funktio f saa arvot [-2,2]. (2 p.)

Ratkaisu yhtälöllä

Ratkaisusta ilmenee korkokerroin 1{,}025 ja kuukausikorko \frac{0{,}025}{12}\,(=0{,}00208333\ldots). (1+1 p.)

Kuukausitalletus on esitetty muuttujana, esimerkiksi ''Olkoon kuukausitalletus x.''

STOP Ilman muuttujaa tai yhtälöä arvostellaan jälkimmäisen arvosteluohjeen mukaan.

Ensimmäinen talletus kasvaa korkoa x *0,025 ensimmäisen vuoden aikana. [1 p.]

Ensimmäisen vuoden jälkeen on tilillä 12x+\frac{0\mathrm{,}025}{12}(1+2+\cdots +12)x. (3 p.)

Vastaavasti lasketaan myös toisen ja kolmannen vuoden aikana talletettujen rahamäärien vaikutus talletusvuonna (ymmärretty, että vuodet ovat samanlaisia + oikealla logiikalla laskettuihin vuosiin perustuva toteutus). (1+1 p.)

Oikea idea siitä, että korolle kertyy korkoa, [1 p.]

eli kolmen vuoden jälkeen tilillä on (12 x +(0,025 /12) *(1 +2 +... +12) x) (1,025^2 +1,025 +1). (1 p.)

Tilin saldon on oltava 7500. Ratkaistaan yhtälö ja saadaan talletuksen suuruudeksi 200\mathrm{,}50 euroa. (1 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Tyyppivirhe: Laskettu vuositalletukseksi 2379{,}05 euroa ja jaettu se kuukausien lukumäärällä 12. Saatu vastaukseksi 198{,}25 euroa (1+0+1+0+1+1+0+0). (max 4 p.)

Huom! Edellisessä tyyppivirheessä vuositalletus voi näkyä ratkaisuissa muuttujana muodossa 12x. Jos ratkaisussa on todettu, että kuukausitalletus on x, niin annetaan myös 2. rivin piste. (max 5 p.)

Tyyppivirhe: Vain yksi talletus. Yksittäinen rahasumma kasvaa korkoa 3 vuotta. x \cdot 1{,}025^3 = 7500, joten x=6964{,}5, ja vastauksena 6964{,}5/36 = 193{,}46. (1+0+1+0+0+1+0+0) (max 3 p.)

TAI Ratkaisu taulukkolaskentaohjelmistolla tai eurolasku ja skaalaus

Ratkaisusta ilmenee korkokerroin 1{,}025. (1 p.)

Taulukosta käy ilmi (mahdollisesti implisiittisesti) ensimmäisen talletuksen korko ensimmäisen vuoden aikana. [1 p.]

Ensimmäinen vuosi on oikein ja oikeat komennot on dokumentoitu. (1+1 p.)

Taulukossa toisen ja kolmannen vuoden korot näkyvät ja ne ovat oikein. (2 p.)

Taulukosta käy ilmi korkoa korolle vaikutus ja oikeat komennot on dokumentoitu. (1+1 p.)

Kokonaisvaikutus on oikein tilin loppusaldon laskussa. (1 p.)

Talletuksen suuruudeksi on saatu 200\mathrm{,}50 euroa. (1 p.)

Ratkaisu sisältää tarpeelliset selitykset, joista nähdään, että tämä on ainoa ratkaisu. (2 p.)

Tähän tehtävään liittyvät erillisohjeet

Jos laskee korkoa korolle kuukausittain korkokertoimella arvostellaan ensimmäisessä skeemassa 2+1+0+0+1+1+0+0. Tämän voi tehdä myös ohjelmiston käskyllä. (max 5 p.)

Alkupiste: Vastauksena kuukausitalletus väliltä 198 − 203 euroa, jota on perusteltu laskemalla tai taulukoimalla. Huom! Tätä pistettä ei saa, jos menetelmä on sellainen, että tälle välille ei päätyisi paitsi pyöristysten seurauksena. (1 p.)

1.

Päättelyssä on virhe, sillä kyseinen pyramidi ei ole puolet oktaedrista. Oktaedrissa jokainen särmä on yhtä pitkä, eikä tässä tapauksessa ole niin. (2 p.)

Puolet pohjan halkaisijasta on 230,3 /sqrt(2), joten Pythagoraan lauseella saadaan sivusärmän pituudeksi sqrt((230,3 /sqrt(2))^2 +146,6^2) ~~219,1, joka ei ole yhtä suuri kuin pohjan sivun pituus TAI laskettu ohjelmistolla. (2 p.)

Todellinen tilavuus on 1/3 *230,3^2 *146,6 ~~2.592.000 kuutiometriä TAI laskettu ohjelmistolla. (2 p.)

Tähän osatehtävään liittyvät erillisohjeet

Alkupiste: Vastauksessa on liikaa/järjetön määrä desimaaleja. TAI Luonnossa oleva pyramidi ei ole matemaattisen pyramidin muotoinen. (1 p.)

Rivillä 1 kelpaa muukin pyramidin ja oktaedrin puolikkaan ilmeinen geometrinen ero. Perustelu erolle vasta rivillä 2.

Vastaus muodossa 2.592\mathrm{e}6 tms. (-1 p.)

2.

Päättelyssä on virhe, sillä Vega ei ole tarkistanut välin päätepisteitä. (Derivoituva funktio voi saada suurimman arvonsa paitsi derivaatan nollakohdassa, myös välin päätepisteessä.) (1 p.)

Todettu, että päättely on muuten oikein TAI täydellinen derivaattatarkastelu. (1 p.)

Oikea ratkaisu menisi siis näin: g'(x) =3 x^2 -2, joten nollakohdat ovat x =+-sqrt(2/3).

Suurin arvo saavutetaan siis jossakin pisteistä x =+-1 tai x =+-sqrt(2/3). [1 p.]

Kulkukaavio sekä oleellisten pisteiden tarkastaminen TAI arvojen laskeminen uusissa pisteissä g(-1)=2 ja g(1)=0 ja vertailu alkuperäisiin: g\left(\sqrt{\frac{2}{3}}\right)=1-\frac{4\sqrt{6}}{9}, g\left(-\sqrt{\frac{2}{3}}\right)=1+\frac{4\sqrt{6}}{9}. (2 p.)

Koska 1 +4 sqrt(6) /9 ~~2,1, suurin arvo on 1 +4 sqrt(6) /9. (1 p.)

Tähän osatehtävään liittyvät erillisohjeet

Ei mainintaa siitä, että päättelyssä on virhe. (0+1+1+2+1) (max 5 p.)

Löydetty virhe päättelyssä, mutta lisäksi väitetty, että päättely on kunnossa, koska vastaus on oikein. (-1 p.)

Löydetty "virheitä", jotka eivät ole virheitä: koko osatehtävästä (-1 p.)

Tehtävän voi ratkaista esimerkiksi käsin tai Pythonilla tai taulukkolaskennalla.

Laskettu oikeiden lukujen osamäärä TAI löydetty oikea kerroin (q_1=1). (1 p.)

Löydetty oikea jakojäännös (r_1=2345801446791). (2 p.)

Jatkettu vastaavasti. (1 p.)

Ensimmäiset kaksi jakojäännöstä oikein (B2–B3). (2 p.)

Näkyvissä rivi, josta voi päätellä vastauksen. (2 p.)

Johtopäätöksenä: Suurin yhteinen tekijä on siis 3. (2 p.)

Laskut dokumentoitu: kaikki laskut (a=q_nb+r_n) näkyvissä TAI kaikki \textrm{(mod)}/remain-rivit näkyvissä TAI taulukkolaskennassa solujen kaavat näkyvissä. (2 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Pienet lasku- ja kopiointivirheet rivistä 5 alkaen (-1 p./virhe)

Jos virheet lyhentävät ratkaisua 5/10/15 riviä, niin lisäksi vähennys [-1/2/3 p.]

Pienet laskuvirheet eivät nollaa Johtopäätöksenä-rivin pisteitä.

Pelkkä taulukko/luvut ilman komentoja tai laskuja, ei dokumentoitu TAI ei kaikkia laskuja näkyvissä. (1+2+1+2+2+2+0) (max 10 p.)

Osamääriä ei laskettu eli q=1 jokaisessa askeleessa. (1+2+1+0+0+0+0+0). (max 4 p.)

Jaettu alkuperäiset luvut kolmella, laskut oikein, saatu suurin yhteinen tekijä kerrotaan kolmella. (max 12 p.)

TAI Koodiratkaisu

Esitetty koodi ohjelmointikielellä, missä:

Koodissa ensimmäiset luvut on alustettu algoritmiin oikein. (1 p.)

Koodi laskee seuraavat luvut oikein ja ne sijoitetaan muuttujiin oikein. (2 p.)

Koodissa on iteraatioehto oikein. (3 p.)

Koodi tulostaa lopussa oikean muuttujan arvon TAI algoritmin kaikki välivaiheet jossakin muodossa (esimerkiksi jakojäännökset). (1 p.)

Ratkaisussa näkyy kokonainen ajettava koodi (esimerkiksi kuvakaappaus). (2 p.)

Ratkaisussa näkyy rivin 4 mukainen oikea tuloste. (1 p.)

Suurin yhteinen tekijä on siis 3. (2 p.)

Tähän tehtävään liittyvät erillisohjeet

Pelkät laskut (selityksiä ei vaadita) TAI oikea Python-koodi ja tuloste. (max 12 p.)

Käytetty syt-komentoa laskimessa tai math.gcd Pythonissa. (+0 p.)

Ratkaisu pythonilla:

            a=123456789101112
              b=121110987654321
              while(b>0):
                  c=a-(a//b)*b
                  a=b
                  b=c
              print(a)
        

Välivaiheet tulostava ratkaisu pythonilla:

            a=123456789101112
              b=121110987654321
              while(b>0):
                  c=a%b
                  q=a//b
                  print(f'{a} = {q} * {b} + {c}')
                  a=b
                  b=c
              print(f'suurin yhteinen tekijä on {a}')
        

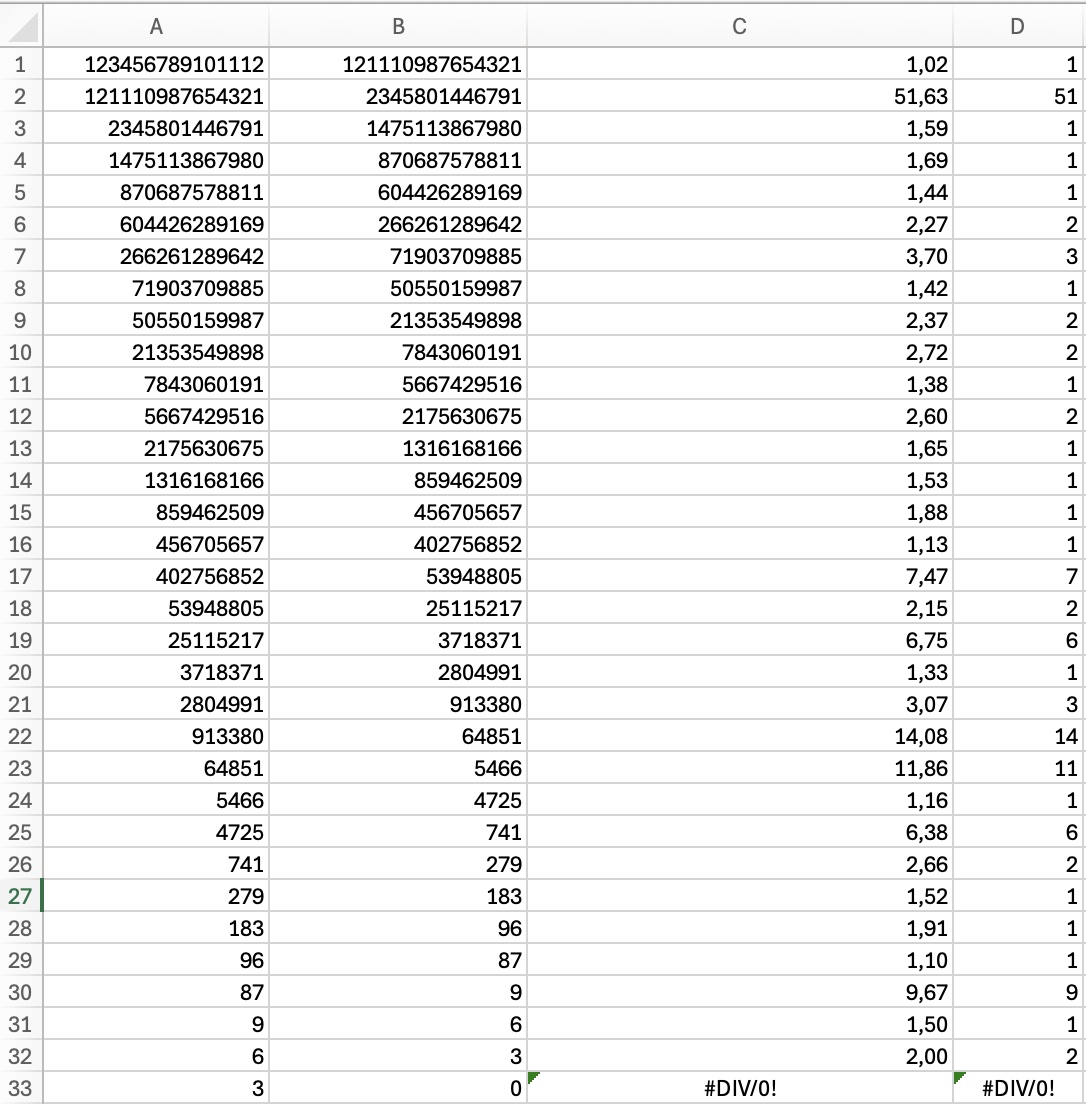
Taulukkolaskennalla tehty ratkaisu, jossa on välivaiheissa esiintyvät luvut:

riippumaton Havainto: polttopisteet ovat ellipsin sisäpuolella. + Perustelu tälle. (1+1 p.)

riippumaton Havainto: Polttopisteet ovat y-akselin suhteen symmetrisesti. + Perustelu tälle. (1+1 p.)

Polttopisteet ovat (-p, 0) ja (p, 0).

riippumaton Sovellettu ellipsin määritelmää pisteeseen (a, 0) TAI (-a, 0) ja saatu yhteys a:n ja k:n välille, esimerkiksi k=(a-p) + (a-(-p)) ~(=2a). (1 p.)

riippumaton Sovellettu ellipsin määritelmää tai symmetriaa pisteeseen (0, 1) TAI (0, -1) ja saatu yhteys p:n ja k:n välille, esimerkiksi k = 2\sqrt{p^2 +1}. (1 p.)

Saatu yhteys a:n ja p:n välille, esimerkiksi 2a=2\sqrt{p^2+1}. (1 p.)

Ratkaistaan yhtälö ja saadaan polttopisteiksi (\pm\sqrt{a^2-1}, 0). (1 p.)

riippumaton Pyritty sijoittamaan piste Z yhtälöön |ZP|+ |ZQ| =k. (1 p.)

Sijoitettu omat polttopisteet ja oma yllä laskettu k ellipsin yhtälöön oikein, esimerkiksi 2a= \sqrt{(x-\sqrt{a^2-1})^2 + y^2} + \sqrt{(x+\sqrt{a^2-1})^2 + y^2} (1 p.)

Dokumentoitu laskimen käyttö sievennyksessä TAI tehty käsin yksi järkevä sievennysaskel. (1 p.)

Päädytty tehtävässä annettuun yhtälöön \frac{x^2}{a^2}+y^2 =1. (1 p.)

Tähän tehtävään liittyvät erillisohjeet

Rivin 1 esimerkkiperustelu: Jos molemmat polttopisteet olisivat pisteen (a, 0) oikealla puolella, etäisyyksien summa ei olisi vakio. Jos taas polttopisteet olisivat pisteen (a, 0) eri puolilla, olisi polttopisteiden välisellä janalla ainakin yksi ellipsin piste. Tällöin k= |PQ| mikä on ristiriita ellipsin määritelmän kanssa.

Rivin 2 esimerkkiperustelu: Ellipsi on symmetrinen koordinaattiakselien suhteen.

Perusteluitta oletettu, että polttopisteet ovat (-p, 0) ja (p, 0) ja esimerkiksi kuvasta käy ilmi, että |p|<a. 1+1+1+1+1+1+1+1+1+1 (max 10 p.)

Alkupiste (1 p.): Todettu sijoittamalla, että pisteet (\pm a, 0) ja (0, \pm 1) ovat käyrällä \frac{x^2}{a^2}+y^2 =1. TAI Ellipsin kuva kiinteällä a:n arvolla ja pisteet merkitty kuvaan tai kerrottu sanallisesti.

1.

Annettu toimivan oloinen kokeilufunktio, joka sisältää ainakin yhden parametrin. (1 p.)

Annettu toimivan oloinen kokeilufunktio, joka (sopivalla parametrivalinnalla) vaihtaa merkkiä välillä [1,2], esimerkiksi g(x)=x-c, johon valitaan sopiva c. (1 p.)

Laskettu integraali \int_1^2 f(x)g(x)\, dx, esimerkkitapauksessa \int_1^2 (3x+2)(x-c)\, dx=10-\frac{13c}{2}. [2 p.]

STOP Ei pisteitä jatkosta, jos integraali laskettu täysin väärällä periaatteella.

Valittu parametri(t) niin, että integraali on nolla: esimerkissä 10-\frac{13c}{2}=0, kun c=\frac{20}{13}. (2 p.)

TAI

Laskettu ortogonaalisuusehtoa vastaava integraali funktiolle f ja jollekin funktiolle g, joka ei ole vakiofunktio. (2 p.)

Edellisen integraalin arvo on 0. (3 p.)

Vastauksena edellä käytetty funktio g. (1 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Integraalin laskennassa ohjelmistossa käytössä likiarvot. (2+2+1) (max 5 p.)

Integraalin arvoa ei aina näy Solve-ratkaisuissa. (-0 p.)

Kokeiltu ainoastaan nollafunktiota.(+0 p.)

TAI

Annettu vastauksena funktio g(x)=h(x)\cdot \frac{1}{3x+2}, (1 p.)

missä h(x) on funktio, jolle on todettu, että selvästi \int_{1}^2 h(x) dx =0 (esimerkiksi h(x)=x-3/2 tai h(x)=\cos (\pi x) tai h(x)=\sin (\pi x + \pi/2)). (2 p.)

Laskettu ortogonaalisuusehdon integraali (joka on nyt = \int_{1}^2 h(x) dx =0) ja saatu 0. (3 p.)

2.

Annettu toimivat f(x), g(x) ja h(x), jotka voivat sisältää parametreja; esimerkiksi f(x)=h(x)=3x+2 ja g(x)=x-\frac{20}{13}. (2 p.)

Osoitettu funktioiden f ja g ortogonaalisuus, samoin funktioille g ja h (tai vedottu osatehtävään 12.1 tai kiinnitetty parametrit). (1+1 p.)

Osoitettu, että f(x) ja h(x) eivät ole ortogonaalisia, esimerkiksi \int_1^2 (3x+2)(3x+2)\, dx=43. (2 p.)

Tähän osatehtävään liittyvät erillisohjeet

Valittu f=h ja g, joka ei ole ortogonaalinen funktioiden f ja h kanssa tai g=0: (1+0+2) (max 3 p.)