Beskrivningar av goda svar: SV – Matematik, lång lärokurs

1.

Riktningskoefficienten är \frac35 och förklarat med uträkning \frac{0-(-3)}{5-0}=\frac{3}{5} eller tydlig figur. (1+1 p.)

Linjens ekvation är y=\frac{3}{5}x-3 och konstanten förklarad exempelvis med hjälp av punkten (0,-3). (1+1 p.)

ELLER

Linjens ekvation har formen y=kx-3 och förklaring: går genom punkten (0,-3) eller använt formen y-(-3)=k(x-0). (1+1 p.)

Linjens ekvation är y=\frac{3}{5}x-3 och förklaring: insättning av den andra punkten (5,0) i ekvationen, varav vi får 0=5k-3, det vill säga k=\frac{3}{5}. (1+1 p.)

Särskilda anvisningar för deluppgiften

Endast svar (1+0)+(1+0) (2 p.)

Svaret kan ges på normalform, till exempel -3x+5y+15=0.

Teckenfel i riktningskoefficienten, koordinaterna i fel ordning el. dyl. (max 3 p.)

Omvända koordinater (fått x=\frac{3}{5}y-3 eller -3y+5x+15=0). (max 3 p.)

2.

f'(x) =6 x +4 e^(4 x) (Första termen 2 p. I den sista termen ger inre och yttre funktionens derivator ett poäng var. Extra termer ger ett poängs avdrag.) (4 p.)

Särskilda anvisningar för deluppgiften

Endast rätt svar. (4 p.)

Extra faktorer (till exempel 4xe^{4x}) (max 3 p.)

3.

int cos(5 x) dx =1/5 sin(5 x) +C, (Koefficienten 1/5 + sin(5 x) + korrekt bortsätt från integreringskonstanten + C.) (4 p.)

Särskilda anvisningar för deluppgiften

Endast rätt svar. (4 p.)

Helt felaktig integrering, men skrivit +C. (1 p.)

1.

Vänsterledet utvecklas till x^2 +2 x -3 eller motsvarande form, varav olikheten får formen x^2 +2 x > 0. (2 p.)

Nollställena utlöses: x^2 +2 x =0, det vill säga x (x +2) =0, varav x =0 eller x =-2. (2 p.)

Det handlar om en parabel som öppnar sig uppåt, så olikhetens lösning är x < -2 eller x > 0. (2 p.)

Särskilda anvisningar för denna lösning

Om endast olikheten behandlats så ges 0 p. från rad 2, max 2+0+2 exempelvis med förklaringen ''eftersom x(x+2) är en parabel som öppnar sig uppåt, så är lösningen x<-2 eller x > 0''.

Förklaringen i rad 3 kan ges även med testvärden.

Endast förklaringspoäng från rad 3 om det är fel polynom eller nollställe i rad 2. 2+0+1 (max 3 p.)

Rätt svar x<-2 eller x > 0 direkt från olikheten x(x+2) > 0 utan förklaring. (2+0+1 p.)

ELLER

Vänsterledet utvecklas till x^2+2x-3 eller motsvarande form, varav olikheten får formen x^2+2x>0. (2 p.)

Tecken för faktorerna i en tabell eller med ord. (2 p.)

Från produktens tecken ser man att olikhetens lösning är x<-2 eller x>0. (2 p.)

2.

Funnit lösningarna x=-e, x=\pi och x=-\pi. (3 p.)

Förklarat via nollregeln (3 p.) ELLER kontroll (1 p.) + ett tredjegradspolynom har högst tre rötter (2 p.). (1+2 p.)

Särskilda anvisningar för deluppgiften

Poäng för produktregeln om dess användning nämnts eller motsvarande ekvationer utskrivna. (2 p.)

Om endast faktoriseringen (x+e)(x-\pi)(x+\pi) används som förklaring, utan att nollregeln nämnts i ord eller som ekvationer. (max 3+1 = 4 p.)

Närmevärden i svaret. (-1 p.)

Försökt använda (\sin x)^2 +(\cos x)^2 =1 + insättning korrekt. (1+1 p.)

Försökt använda \sin (2x)=2\sin (x)\cos (x) + insättning korrekt. (1+1 p.)

STOP Poäng från fortsättningen bara om rad 1 eller rad 2 är korrekt.

Brutit ut (\sin x)^2 som gemensam faktor och fått ekvationen (\sin x)^2(1-4(\cos x)^2)=0 ELLER tagit bort kvadrattecknet korrekt och fått ekvationen \sin(x) = \pm 2 \sin(x)\cos(x). (1 p.)

Fortsatt med nollregeln. (Poäng bara om föregående rad gett 1 p.) (1 p.)

Från ekvationen \sin x=0 fått lösningarna ganska exakt x=0 och ganska exakt x=\pm \pi (utan förklaring). (1+1 p.)

Från ekvationen \cos x=\pm \frac{1}{2} fått lösningarna ganska exakt x=\pm \frac{\pi}{3} och ganska exakt x=\pm \frac{2\pi}{3}, exempelvis med formeln för allmän lösning eller med annan förklaring.
(Förklaring 2 p. + lösningar: hälften 1 p. + resten 1 p.) (2+2 p.)

ELLER

Försökt använda (\sin x)^2 = 1-(\cos x)^2 + insättning korrekt. (1+1 p.)

STOP Poäng från fortsättningen bara om rad 1 är korrekt.

Fått ekvationen (\sin x)^2 = (\sin(2x))^2.

Tagit bort kvadrattecknet korrekt och fått ekvationen \sin(x) = \pm \sin(2x). (1+1 p.)

Från ekvationen \sin x = \sin(2x) fått lösningen ganska exakt x=0 (utan förklaring). (1 p.)

Löst ekvationen \sin x = \sin(2x), fått lösningarna ganska exakt x=\pm \pi, ganska exakt x=\pm \frac{\pi}{3}. (x=2x+2\pi k (1 p.), x=2\pi k+\pi-2x (1 p.), lösningar: hälften (1 p.) + resten (1 p.)) (2+2 p.)

Löst ekvationen \sin x = -\sin(2x), fått lösningarna ganska exakt x=\pm \frac{2\pi}{3} (2 p.) OCH ganska exakt x=0 och ganska exakt x= \pm \pi (1 p.). (3 p.)

ELLER

Skrivit om (\cos x)^2 på rimlig form, t.ex. \cos^2(x) = \frac12 (1+\cos(2x)) och satt in detta i ekvationen. (1+1 p.)

Skrivit om (\sin(2x))^2 på rimlig form, t.ex. \sin^2(2x) = \frac12 (1-\cos(4x)) och satt in detta i ekvationen. (1+1 p.)

STOP Poäng från fortsättningen bara om rad 1 eller rad 2 är korrekt.

Ur ekvationen fått ganska exakt x=0 (utan förklaring). (1 p.)

Från den erhållna ekvationen löst (2 p.) ganska exakt x=\pm \pi, ganska exakt x=\pm \frac{\pi}{3}. (2 p.) (2+2 p.)

Från ekvationen löst ganska exakt x=\pm \frac{2\pi}{3}. (3 p.)

Särskilda anvisningar för uppgiften

Svarspoängen från de två sista raderna i schema 2 och 3 förutsätter att lösningarna fåtts med förklaring.

Startpoäng (1 p.): En eller alla lösningar gissade och testade.

Svaret innehåller en rot som inte är en lösning till ekvationen ifråga. Avdrag -1 p./st. från den rad där felet uppstått.

Begränsningen av lösningarna behöver inte förklaras, utan det räcker att finna rätt värden. Om lösingarna inte begränsats, t.ex. \pi +k2\pi, eller om gränsvillkoret x\in [-\pi,\pi] använts fel: -1 poäng per rad där felet gjorts. Gäller de sista två raderna.

Korrekt lösning med grader, fått svar -180,-120,-60, 0, 60,120 och 180 grader. (max 12 p.)

Som en lösning till ekvationen räcker det inte att gissa och testa nollställen.

1.

Ursprungliga medelvärdet på någon form, exempelvis a = \frac{x_1 + \dots +x_n}{n} eller x_1 + \dots +x_n = an. (1 p.)

Nya medelvärdet på någon form, exempelvis \frac{x_1 + \dots +x_n +b}{n+1}. (1 p.)

Jämfört medelvärdena på rimligt sätt, exempelvis differens eller kvot eller bildat olikheten "ursprungligt mv" < "ny mv". (1 p.)

Rimligt omvandlingssteg, till exempel multiplicerat bort nämnarna eller förlängt till en gemensam nämnare. (1 p.)

Skrivit om på passande form och använt villkoret a<b. (1+1 p.)

ELLER

Det ursprungliga medelvärdet ändras inte om vi lägger till a OCH förklaring till detta. (1+2 p.)

Om vi lägger till talet b, som är större än a, växer medelvärdet OCH förklaring till detta. (2+1 p.)

Särskilda anvisningar för denna lösning

Man behöver inte nämna att talen n och n+1 är positiva.

Exempellösning: \frac{x_1+x_2+\cdots +x_n+b}{n+1} =\frac{na+b}{n+1} >\frac{na+a}{n+1}=a.

Särskilda anvisningar för deluppgiften

Påståendet \Rightarrow \dots \Rightarrow a<b. (-0 p.)

2.

Givit ett fungerande exempel. (2 p.)

Givit ett exempel med minst tre olika tal:

oberoende Visat att typvärdet i exemplet är 1. (1 p.)

oberoende Visat att medianen i exemplet är 100. (1 p.)

oberoendeVisat att medelvärdet i exemplet är 10. (2 p.)

Särskilda anvisningar för denna lösning

Om medelvärdet \ne 10, men ett närmevärde har beräknats korrekt och ligger inom intervallet [9{,}5;10{,}5[, så ger sista raden 1 p.

Om flera olika exempel givits, ges poäng i ovanstående oberoende-rader bara för ett av exemplen. (max 2 p.)

ELLER (Konstruktion av ett exempel: poäng för raderna ges endast om egenskapen ifråga gäller för det GIVNA (möjligen bristfälliga) exemplet)

Konstruktionen innehåller en idé om hur man får typvärdet 1. (1 p.)

oberoende Konstruktionen innehåller en idé om hur man får medianen 100. (1 p.)

oberoende Konstruktionen innehåller en idé om hur man får medelvärdet 10. (1 p.)

Färdigställt kostruktionen, exempelvis löst återstående fria variabler. (1 p.)

Givit ett fungerande exempel, såsom -338, 1, 1, 100, 101, 102, 103. (2 p.)

Löst ut y eller x från cirkelns ekvation: y=\pm \sqrt{4-x^2} eller x=\pm \sqrt{4-y^2}. (2 p.)

oberoende Noterat att x\in [-2,2] ELLER y\in [-2,2]. (1 p.)

Insatt fallet y=+\sqrt{4-x^2} : f(x,\sqrt{4-x^2})=x\sqrt{4-x^2}. (1 p.)

Idé om derivering + korrekt derivering:
D(x\sqrt{4-x^2})=\sqrt{4-x^2}+\frac{x\cdot (-2x)}{2\sqrt{4-x^2}}\ (=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}) (då -2<x<2). (1+1 p.)

Alltså gäller \sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}=\frac{4-2x^2}{\sqrt{4-x^2}}=0 då x=\pm \sqrt{2}. (1 p.)

Beräknat värdena i derivatans nollställen och i ändpunkterna ELLER teckenschema: f(2,0)=0, f(-2,0)=0 och f(\sqrt{2},\sqrt{2})=2, f(-\sqrt{2},\sqrt{2})=-2. (2 p.)

På denna halvcirkel är uttryckets minsta värde -2 och det största värdet 2, så f får (på grund av kontinuitet) värdena [-2,2]. (1+1 p.)

Påpekat att fallet x= -\sqrt{4-y^2} eller y= - \sqrt{4-x^2} är symmetriskt och f får samma värden där. (1 p.)

Särskilda anvisningar för denna lösning

\pm saknas på rad 1 och symmetrin inte behandlad på annat sätt (1+1+1+2+1+2+2+0) (max 10 p.)

Annat fel på rad 1 än saknat \pm (felaktigt borttaget rottecken el. dyl.), endast idépoäng för deriveringen. (0+1+1+(1+0)+1+2+(0+0)+1) (max 7 p.)

Endast beräknat f(-2,0) eller f(2,0) (+0 p.)

ELLER

Cirkeln har radien 2 och är centrerad i origo. [1+1 p.]

Cirkelns ekvation på parameterform är \begin{cases} x=2\cos t \\ y=2\sin t, \end{cases} (där t\in[0,2\pi].) (2 p.)

Satt in x och y i ekvationen för funktionen f, fått f(t)=2\cos t\cdot 2 \sin t=4\cos t \sin t (2 p.)

=2\sin (2t) (2 p.)

Funktionen \sin (2t) får värdena [-1,1] (på intervallet t\in [0,2\pi]), (2 p.)

så funktionen f får värdena [-2,2]. (2 p.)

Lösning med ekvation

Ur lösningen framgår räntekoefficienten 1{,}025 och månadsräntan \frac{0{,}025}{12}\,(=0{,}00208333\ldots). (1+1 p.)

Introduktionen av den efterfrågade pengosumman som variabel, t.ex. "låt x beteckna den på sparkontot månatligen insatta summan".

STOP Lösningar utan vare sig variabel eller ekvation poängsätts enligt det nedre schemat.

Till den första bankinsättningen läggs en ränta på x *0,025 under det första året. [1 p.]

Efter det första året är saldot för sparkontot 12x+\frac{0\mathrm{,}025}{12}(1+2+\cdots +12)x. (3 p.)

Räntans inverkan på de under andra jämte tredje året insatta summorna under insättningsåret beräknas på samma sätt (studenten inser att räntan alltid har en likadan inverkan under insättningsåret + beräknar den med rätt princip). (1+1 p.)

Rätt idé om ränta på ränta, [1 p.]

dvs. efter tre år är saldot för kontot (12 x +(0,025 /12) *(1 +2 +... +12) x) (1,025^2 +1,025 +1). (1 p.)

Saldot efter tre år skall bli 7500. Genom att lösa ekvationen fås den månatligen insatta summan som 200\mathrm{,}50 euro. (1 p.)

Särskilda anvisningar för uppgiften

Typfel: Den årligen insatta summan beräknas som 2379{,}05 euro och den delas med 12 för att få den månatliga summan. Svaret blir 198{,}25 euro (1+0+1+0+1+1+0+0). (max 4 p.)

Obs! I det ovanstående typfelet kan den årliga sammanlagda insättningen ibland betecknas som 12x. Om variabelns betydelse som den månatliga insättningen förklaras, delas också den andra radens poäng. (max 5 p.)

Typfel: Endast en insättning som antas samla ränta i 3 år: x \cdot 1{,}025^3 = 7500, så x=6964{,}5, och svaret ges som 6964{,}5/36 = 193{,}46. (1+0+1+0+0+1+0+0) (max 3 p.)

ELLER Lösning med kalkylbladsprogram eller "ett euros insättning och skalning"

Ur lösningen framgår räntekoefficienten 1{,}025. (1 p.)

Ur kalkylbladet framgår (eventuellt implicit) den ovanpå den första insättningen under första året tillagda räntan. [1 p.]

Det första året är korrekt beräknat och dokumeteringen visar att kommandona är rätta. (1+1 p.)

Ur kalkylbladet framgår andra och tredje årets räntor och de är rätta. (2 p.)

Att ränta läggs på ränta framgår ur kalkylbladet och de rätta kommandona är dokumenterade. (1+1 p.)

Den totala inverkan är rätt i beräkningen av slutsaldot. (1 p.)

Som den månatligen insatta summan fås 200\mathrm{,}50 euro. (1 p.)

Till lösningen fogas en förklaring som klargör att det inte finns andra lösningar. (2 p.)

Särskilda anvisningar för uppgiften

Fallet att ränta läggs på ränta i lösningen varje månad poängsätts i det första schemat som 2+1+0+0+1+1+0+0. Motsvarande fall kan förekomma i kalkylbladslösningar. (max 5 p.)

Startpoäng: Som svar anges en månatlig insättningssumma i intervallet 198 − 203 euro, och svaret motiveras med beräkningar eller kalkyltabeller. Obs! Detta startpoäng tilldelas inte om svaret ligger i detta intervall endast efter avrundning. (1 p.)

1.

Slutledningen är felaktig, eftersom pyramiden ifråga inte är en halv oktaeder. I en oktaeder är alla kanter lika långa, vilket inte är fallet i denna pyramid. (2 p.)

Halva diametern av basytan är 230,3 /sqrt(2), så enligt Pythagoras sats är kanten från pyramidens topp till ett av dess hörn sqrt((230,3 /sqrt(2))^2 +146,6^2) ~~219,1, vilket inte är lika med sidlängden av basen ELLER räknat med programvara. (2 p.)

Den riktiga volymen är 1/3 *230,3^2 *146,6 ~~2.592.000 kubikmeter ELLER räknat med programvara. (2 p.)

Särskilda anvisningar för deluppgiften

Startpoäng: Svaret har för många / orimligt många decimaler. ELLER En pyramid i verkligheten är inte formad som en matematisk pyramid. (1 p.)

På rad 1 duger även andra uppenbara geometriska skillnader mellan pyramiden och en halv oktaeder. Förklaring till skillnaden först på rad 2.

Svar på formen 2.592\mathrm{e}6 el. dyl. (-1 p.)

2.

Slutledningen innehåller fel, eftersom Vega inte kontrollerat intervallets ändpunkter. (En deriverbar funktion kan anta sina största värden antingen i derivatans nollställen eller i definitionsintervallets ändpunkter.) (1 p.)

Noterat att slutsatsen är annars korrekt ELLER fullständig derivatastudie. (1 p.)

En korrekt lösning skulle alltså gå enligt följande: g'(x) =3 x^2 -2, så derivatans nollställen är x =+-sqrt(2/3).

Största värdet antas alltså i någon av punkterna x =+-1 eller x =+-sqrt(2/3). [1 p.]

Teckenstudie och kontroll i de relevanta punkterna ELLER beräknat värdet i de nya punkterna g(-1)=2 och g(1)=0 och jämfört med de ursprungliga g\left(\sqrt{\frac{2}{3}}\right)=1-\frac{4\sqrt{6}}{9}, g\left(-\sqrt{\frac{2}{3}}\right)=1+\frac{4\sqrt{6}}{9}. (2 p.)

Eftersom 1 +4 sqrt(6) /9 ~~2,1, så är det största värdet 1 +4 sqrt(6) /9. (1 p.)

Särskilda anvisningar för deluppgiften

Inte nämnt att slutledningen innehåller fel. (0+1+1+2+1) (max 5 p.)

Funnit felet i slutledningen, men också hävdat att slutledningen är korrekt eftersom svaret är rätt. (-1 p.)

Funnit "fel" som inte är fel: från hela deluppgiften (-1 p.)

Uppgiften kan lösas exempelvis för hand eller med Python eller kalkylprogram.

Beräknat kvoten mellan rätt tal ELLER funnit rätt koefficient (q_1=1). (1 p.)

Funnit rätt rest (r_1=2345801446791). (2 p.)

Fortsatt på motsvarande sätt. (1 p.)

De första två resterna korrekt (B2–B3). (2 p.)

En rad från vilken svaret kan läsas ut synlig. (2 p.)

Slutsats: Den största gemensamma delaren är alltså 3. (2 p.)

Beräkningarna dokumenterade: alla räkningar (a=q_nb+r_n) synliga ELLER alla \textrm{(mod)}/remain-rader synliga ELLER i ett kalkylblad cellernas formler synliga. (2 p.)

Särskilda anvisningar för denna lösning

Små räkne- och kopieringsfel från och med rad 5 (-1 p./fel)

Om felen förkortar lösningen med 5/10/15 rader, ges ytterligare avdrag [-1/2/3 p.]

Små räknefel nollställer inte poängen från Slutsats-raden.

Endast tabell/tal utan kommentarer eller uträkningar, ingen dokumentation ELLER inte alla räkningar synliga. (1+2+1+2+2+2+0) (max 10 p.)

Kvoterna inte beräknade, alltså q=1 i varje rad. (1+2+1+0+0+0+0+0). (max 4 p.)

Dividerat de ursprungliga talen på tre, korrekta räkningar och slutligen multiplicerat den erhållna största gemensamma delaren med tre. (max 12 p.)

ELLER Kodningslösning

Presenterat kod i ett programmeringsspråk, där:

De första talen är i koden korrekt initierade i algoritmen. (1 p.)

Koden beräknar följande tal korrekt och insätter dessa som variabelvärden korrekt. (2 p.)

Iterationsvillkoret är korrekt i koden. (3 p.)

Koden skriver i slutet ut värdet på rätt variabel ELLER alla mellansteg på någon form (till exempel heltalsresterna). (1 p.)

I lösningen syns en fullständig körbar kod (till exempelvis skärmdump). (2 p.)

I lösningen syns korrekt utskrift enligt rad 4. (1 p.)

Den största gemensamma delaren är alltså 3. (2 p.)

Särskilda anvisningar för uppgiften

Endast räkningar (förklaringar behövs ej) ELLER korrekt Python-kod och utskrift. (max 12 p.)

Använt sgd-kommandot på räknare eller math.gcd i Python. (+0 p.)

Lösning med Python:

            a=123456789101112
              b=121110987654321
              while(b>0):
                  c=a-(a//b)*b
                  a=b
                  b=c
              print(a)
        

Lösning som skriver ut mellanleden med Python:

            a=123456789101112
              b=121110987654321
              while(b>0):
                  c=a%b
                  q=a//b
                  print(f'{a} = {q} * {b} + {c}')
                  a=b
                  b=c
              print(f'den största gemensamma delaren är {a}')
        

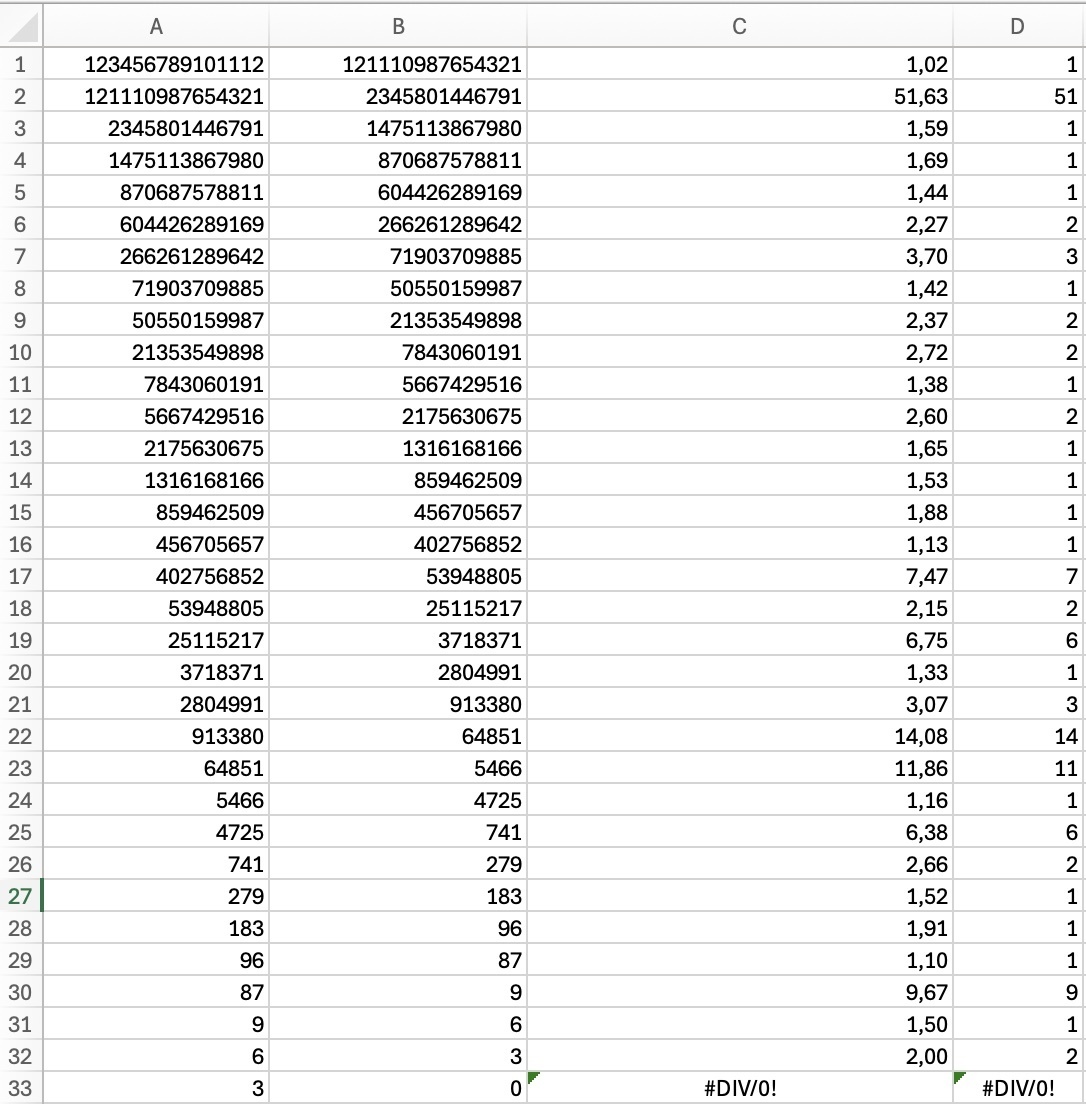
Lösning gjord i kalkylblad, som innehåller de tal som ingår i mellanleden:

oberoende Observation: brännpunkterna ligger inuti ellipsen. + Förklaring till detta. (1+1 p.)

oberoende Observation: brännpunkterna är symmetriska med avseende på y-axeln. + Förklaring till detta. (1+1 p.)

Brännpunkterna är (-p, 0) och (p, 0).

oberoende Tillämpat ellipsens definition till punkten (a, 0) ELLER (-a, 0) och fått ett samband mellan a och k, till exempel k=(a-p) + (a-(-p)) ~(=2a). (1 p.)

oberoende Tillämpat ellipsens definition eller symmetri till punkten (0, 1) ELLER (0, -1) och fått ett samband mellan p och k, till exempel k = 2\sqrt{p^2 +1}. (1 p.)

Fått ett samband mellan a och p, t.ex. 2a=2\sqrt{p^2+1}. (1 p.)

Löst ekvationen och fått brännpunkterna (\pm\sqrt{a^2-1}, 0). (1 p.)

oberoende Försökt sätta in punkten Z i ekvationen |ZP|+ |ZQ| =k. (1 p.)

Satt in de egna brännpunkterna och det egna ovan beräknade värdet k korrekt i ellipsens ekvation, till exempel 2a= \sqrt{(x-\sqrt{a^2-1})^2 + y^2} + \sqrt{(x+\sqrt{a^2-1})^2 + y^2} (1 p.)

Dokumenterat användningen av räknare i förenklingen ELLER gjort ett rimligt förenklingssteg för hand. (1 p.)

Kommit fram till den i uppgiften givna ekvationen \frac{x^2}{a^2}+y^2 =1. (1 p.)

Särskilda anvisningar för uppgiften

Exempelförklaring för rad 1: Om båda brännpunkterna skulle ligga till höger om (a, 0), skulle summan av avstånden inte vara konstant. Om brännpunkterna låg på olika sidor om (a, 0), så skulle minst en av punkterna på ellipsen ligga mellan brännpunkterna. Då skulle k= |PQ|, vilket strider mot ellipsens definition.

Exempelförklaring för rad 2: Ellipsen är symmetrisk med avseende på koordinataxlarna.

Utan förklaring antagit att brännpunkterna är (-p, 0) och (p, 0) och det framgår exempelvis av en figur att |p|<a. 1+1+1+1+1+1+1+1+1+1 (max 10 p.)

Startpoäng (1 p.): Visat genom insättning att punkterna (\pm a, 0) och (0, \pm 1) ligger på kurvan \frac{x^2}{a^2}+y^2 =1. ELLER Figur av ellipsen för ett given värde på a och punkterna markerade i figuren eller beskrivna i ord.

1.

Givit en rimlig testfunktion som innehåller minst en parameter. (1 p.)

Givit en rimlig testfunktion som (med ett passande parametervärde) byter tecken på intervallet [1,2], till exempel g(x)=x-c, där c väljs på ett passande sätt. (1 p.)

Beräknat integralen \int_1^2 f(x)g(x)\, dx, i exempelfallet \int_1^2 (3x+2)(x-c)\, dx=10-\frac{13c}{2}. [2 p.]

STOP Inga poäng för fortsättningen om integralen beräknats enligt helt fel principer.

Valt parametern / parametrarna så att integralen blir noll: i exemplet 10-\frac{13c}{2}=0 väljs c=\frac{20}{13}. (2 p.)

ELLER

Beräknat en integral som svarar mot ortogonalitetsvillkoret för funktionen f och någon icke-konstant funktion g. (2 p.)

Värdet av integralen ovan är 0. (3 p.)

Som svar givit funktionen g ovan. (1 p.)

Särskilda anvisningar för denna lösning

Använt närmevärden då integralen beräknats med programvara. (2+2+1) (max 5 p.)

Integralens värde syns inte alltid i en Solve-lösning. (-0 p.)

Endast testat nollfunktionen.(+0 p.)

ELLER

Som svar givit funktionen g(x)=h(x)\cdot \frac{1}{3x+2}, (1 p.)

där h(x) är en funktion för vilken det påpekats att \int_{1}^2 h(x) dx =0 (till exempel h(x)=x-3/2 eller h(x)=\cos (\pi x) eller h(x)=\sin (\pi x + \pi/2)). (2 p.)

Beräknat integralen i ortogonalitetsvillkoret (som nu är = \int_{1}^2 h(x) dx =0) och fått 0. (3 p.)

2.

Givit fungerande f(x), g(x) och h(x), som kan innehålla parametrar; exempelvis f(x)=h(x)=3x+2 och g(x)=x-\frac{20}{13}. (2 p.)

Visat att funktionerna f och g är ortogonala, liksom funktionerna g och h (eller hänvisat till deluppgift 12.1 eller fixerat parametrarna). (1+1 p.)

Visat att f(x) och h(x) inte är ortogonala, exempelvis \int_1^2 (3x+2)(3x+2)\, dx=43. (2 p.)

Särskilda anvisningar för deluppgiften

Valt f=h och g, som inte är ortogonal mot f och h eller g=0: (1+0+2) (max 3 p.)