Hyvän vastauksen piirteet: FI – Matematiikka, lyhyt oppimäärä

25.9.2025

Lopulliset hyvän vastauksen piirteet 13.11.2025

Lopullisista hyvän vastauksen piirteistä ilmenevät perusteet, joiden mukaan koesuorituksen lopullinen arvostelu on suoritettu. Tieto siitä, miten arvosteluperusteita on sovellettu kokelaan koesuoritukseen, muodostuu kokelaan koesuorituksestaan saamista pisteistä, lopullisista hyvän vastauksen piirteistä ja lautakunnan määräyksissä ja ohjeissa annetuista arvostelua koskevista määräyksistä. Lopulliset hyvän vastauksen piirteet eivät välttämättä sisällä ja kuvaa tehtävien kaikkia hyväksyttyjä vastausvaihtoehtoja tai hyväksytyn vastauksen kaikkia hyväksyttyjä yksityiskohtia. Koesuorituksessa mahdollisesti olevat arvostelumerkinnät katsotaan muistiinpanoluonteisiksi, eivätkä ne tai niiden puuttuminen näin ollen suoraan kerro arvosteluperusteiden soveltamisesta koesuoritukseen.

Hyvästä suorituksesta näkyy, miten vastaukseen on päädytty. Ratkaisussa on oltava tarvittavat laskut tai muut riittävät perustelut sekä lopputulos. Arvioinnissa kiinnitetään huomiota kokonaisuuteen, ja ratkaisu pyritään arvioimaan kolmiosaisesti: alku, välivaiheet ja lopputulos. Laskuvirheet, jotka eivät olennaisesti muuta tehtävän luonnetta, eivät alenna pistemäärää merkittävästi. Sen sijaan tehtävän luonnetta muuttavat lasku- ja mallinnusvirheet saattavat alentaa pistemäärää huomattavasti.

Matemaattiset ohjelmistot ovat kokeen apuvälineitä, joiden roolit arvioidaan tehtäväkohtaisesti. Jos ratkaisussa on käytetty ohjelmistoja, sen on käytävä ilmi suorituksesta. Analysointia vaativien tehtävien ratkaisemisessa pelkkä ohjelmistolla saatu vastaus ei riitä ilman muita perusteluja. Sen sijaan ohjelmasta saatu tulos yleensä riittää rutiinitehtävissä ja laajempien tehtävien rutiiniosissa. Tällaisia ovat esimerkiksi lausekkeiden muokkaaminen, yhtälöiden ratkaiseminen sekä funktioiden derivointi ja integrointi.

Miten pisteytysohjeita luetaan

  • Ohjeen rakenne
    • Ohjeessa riviksi kutsutaan kokonaisuutta, joka päättyy pistemäärään.
    • Rivin useat pisteet on erotettu /-merkillä. Epäselvissä tapauksissa on suluissa eritelty, mistä osasta saa mitäkin pisteitä.
    • Erittelyä ei ole, jos rivillä on saman verran laskuja kuin pisteitä, tällöin yksi piste laskua kohden.
    • Jos rivillä on yksi lasku ja siihen liittyvä sanallinen perustelu, niin puolet pisteistä (pyöristettynä ylös) saa laskusta ja loput perusteluista.
    • Jos rivillä on vain yksi lasku tai kaava ja useampi piste, saa osapisteet riittävän hyvästä yrittämisestä (esimerkiksi derivaatan laskeminen osittain oikein).
    • Rivillä suluissa oleva lasku tai perustelu on lisätietoa, eikä sitä vaadita pisteiden saamiseen.
    • Hakasuluissa olevat pisteet saa joko täyttämällä sen rivin ehdon tai seuraavalta riviltä, jos seuraava rivi on kunnossa, eikä käy eksplisiittisesti ilmi, että edellinen rivi on tehty väärin.
  • Jos erikseen ei mainita, niin vastauksen hyväksyttävä tarkkuus on yksi merkitsevä numero enemmän tai vähemmän kuin ohjeeseen kirjattu.
  • Yleensä laskuvirhe vähentää pisteitä siitä rivistä, johon se kohdistuu, mutta myöhempien rivien pisteet voi saada, jos tekee laskut/päättelyt oikein omille luvuille. Poikkeukset on merkitty tekstillä täsmälleen. Nämä pisteet saa vain, jos tämä askel ja myös edeltävät askeleet on oikein suoritettu. Huomaa, että teksti täsmälleen tarkoittaa sitä, että kaikkien niiden rivien, jotka eivät ole riippumattomia, täytyy olla perusteluineen kunnossa. (Tällöin ratkaisussa on ekvivalenttia muotoilua vaille ohjeeseen merkitty luku/lauseke/tms.) Tämä ei vaikuta pyöristysten pisteyttämiseen. Jos esimerkiksi vastausrivillä lukee täsmälleen 37, niin myös 37,5 ja 40 kelpaavat. Tekstillä melko täsmälleen merkitseminen tarkoittaa sitä, että luvut ja laskut pitää olla kunnossa, mutta perusteluissa ja selityksissä voi olla puutteita.
  • Rivien riippuvuus toisistaan
    • Yleensä pisteytys on kirjoitettu ratkaisun matemaattisen etenemisen mukaisesti ja (täysiä) pisteitä annetaan vain perustelluista askeleista. Jos rivit ovat ilmeisen riippumattomia toisistaan (esimerkiksi laskettu eri funktioiden derivaatat), niin pisteet annetaan suoritusjärjestyksestä riippumatta ilman eri merkintää.
    • Jos vastaus on kirjoitettu ennen perusteluja, tarkoittaa se, että pelkästä (oikeasta) vastauksesta saa jo pisteitä.
    • Merkintä yllä olevista riveistä riippumaton piste tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit edellyttävät tätä riviä normaaliin tapaan.
    • Merkintä riippumaton tarkoittaa, että rivin pisteet voi antaa edellä olevista riveistä riippumattomasti; seuraavat rivit eivät edellytä tätä riviä.
    • Merkintä Johtopäätöksenä: korostaa, että kyseiset pisteet saa vain, jos aiemmat perustelut ovat kunnossa.
    • Teksti STOP tarkoittaa sitä, että sillä rivillä kerrotaan, minkä ehtojen pitää toteutua, jotta jatkosta saa pisteitä.
  • Terminologiaa
    • "Vastaus riittää" tarkoittaa, että oikeasta vastauksesta annetaan pisteet myös ilman perusteluja. Jos vastaus on väärin, voi pisteitä saada normaalien periaatteiden mukaisesti perustelujen perusteella.
    • "Alkupisteitä" tarkoittaa, että tästä voi antaa rivin pisteet, jos ei muualta saa pistettä. Tätä pistettä ei siis voi yhdistää muihin pisteisiin.
    • "maxN" tarkoittaa, että tämän tyyppisestä ratkaisusta annetaan N pistettä, mikäli siinä ei ole muita virheitä.
    • "Vastaus vain likiarvona" tarkoittaa, että ratkaisussa ei ilmene lainkaan vastauksen tarkkaa arvoa.

Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta ansaittuja pisteitä ei voi menettää.

  • Vastaus oikein, muttei pyydetyssä muodossa (esimerkiksi tarkkuus, yksikkö) -1 p.
  • Vastaus sieventämättä loppuun asti sievennystehtävässä (esimerkiksi e^1, ln (e) tai 4^0) -2 p.
  • Vastaus sieventämättä muussa tehtävässä (esimerkiksi e^1, ln (e) tai 4^0) -1 p.
  • Ilmeiset näppäilyvirheet esityksessä (esimerkiksi x =2, y04), tai näppäilyvirheet, jotka korjataan heti seuraavalla rivillä -0 p.
  • Vastauksessa kopiointivirhe -1 p.
  • Välipyöristyksessä ei yhtä enemmän merkitseviä numeroita kuin vastauksessa -1 p.

Seuraavat vähennykset ovat tehtäväkohtaiseen pisteohjeeseen toissijaisia. Yhteen tehtävään voi soveltaa useaa vähennystä, mutta kutakin korkeintaan kerran.

  • Matemaattisesti puutteellinen merkintä (esimerkiksi puuttuvat sulut, mutta laskettu oikein; =-merkin ketjutus, m^2 ilman m). Huom.! Tilanteesta riippuen epästandardi merkintä voidaan hyväksyä selitettynä. -1 p.
  • Ratkaisusta puuttuu oleellisia selityksiä (lukija joutuu arvaamaan, mitä ratkaisussa esiintyvät luvut tarkoittavat) TAI perustelut ja johtopäätökset on esitetty täysin irrallisina (lukija joutuu yhdistelemään eri puolilla ratkaisua olevia lauseita) -1 p.
  • Ratkaisussa merkittävästi ylimääräistä tekstiä/laskuja (lukija joutuu päättelemään, miten annetuista tiedoista muodostuu ratkaisu) -1 p.

A-osa

1. Lyhyitä tehtäviä 12 p.

Anna tässä tehtävässä pelkkä vastaus ilman perusteluja. Vastauslaatikkoon voi kirjoittaa vain yhden kokonaisluvun.

1.1 Kuinka monta prosenttia 36 on luvusta 45?  2 p.

  • 80 (2 p.)

1.2 Tilille on juuri maksettu 3 prosenttia korkoa, minkä jälkeen tilillä on 675,68 euroa. Kuinka paljon tilillä oli rahaa ennen koron maksamista?  2 p.

  • 656 (2 p.)

1.3 Laske f(16), kun f(x) =sqrt(x) -2.  2 p.

  • 2 (2 p.)
  • 4 (1 p.)
Virheellinen vastaus, joka antaa pisteen (vähennyslasku unohtunut): 4.

1.4 Kuinka monta erisuurta nollakohtaa polynomilla p(x) =x^2 +6 x +9 on?  2 p.

  • 1 (2 p.)

1.5 Mikä on todennäköisyys saada kahden kolikon heitossa kaksi klaavaa? Anna vastaus prosentteina.  2 p.

  • 25 (2 p.)

1.6 Kuinka monella tavalla voidaan saada pienen ja suuren tavallisen nopan heitossa silmälukujen summaksi 6?  2 p.

  • 5 (2 p.)

2. Osuus äänistä 12 p.

Presidenttiehdokas A sai 7,3 % kaikista ennakkoäänistä ja 12,7 % kaikista vaalipäivän äänistä. Yhteensä hyväksyttyjä ääniä annettiin 2 500 000, joista 32 % oli ennakkoääniä. Mikä oli ehdokkaan A saamien äänien prosenttiosuus kaikista hyväksytyistä äänistä?

Ennakkoääniä oli 0,32 *2.500.000 =800.000. (2 p.)

Vaalipäivänä annettiin siis 2.500.000 -800.000 =1.700.000 TAI (1-0.32)\cdot 2.500.000(=0.68\cdot 2.500.000)=1.700.000 ääntä. (2 p.)

Vaalipäivänä ehdokas sai 0,127 *1.700.000 =215.900 (2 p.)

ja ennakkoon 0,073 *800.000 =58.400 ääntä. (2 p.)

Ehdokkaan ääniosuus on siis (215.900 +58.400) /2.500.000 =(274.300/2.500.000), (summa + osamäärä) (2 p.)

= melko täsmälleen 0,10972 eli noin 11 % TAI 10 % TAI 11,0 % (vain nämä tarkkuudet). (2 p.)

Tähän tehtävään liittyvät erillisohjeet

Neljällä ensimmäisellä rivillä oikea idea 1 p. + oikean idean oikea toteutus 1 p.

Jos tyhjästä ilmestyy jotain riviä 1–4 vastaava oikea luku, niin se antaa yhden pisteen sitä vastaavalta riviltä. Tyhjästä ilmestyvästä väärästä luvusta ei pisteitä vaikka luku olisikin niin lähellä oikeaa, että voisi kuvitella logiikan olevan oikein.

Omilla luvuilla voi saada yhden pyöristyspisteen ellei osamäärän idea ole väärä.

3. Uppotunneli 12 p.

Sanomalehdessä (HBL, 21.10.2023) kerrottiin 18 kilometriä pitkästä Fehmarnin Beltin tunnelista, jonka pitäisi suunnitelmien mukaan valmistua vuonna 2029. Uppotunneli yhdistää Lollandin ja Fehmarnin saaret, ja siitä tulee maailman pisin omassa lajissaan.

Projektin johtaja kertoo, että tunnelin rakentamiseen tarvittavan betonin määräksi arvioidaan kolme miljoonaa kuutiometriä. Hän lisää, että tämä määrä riittäisi koko päiväntasaajan ympäri kiertävän jalkakäytävän rakentamiseen. Arvioi, kuinka korkea tällainen betonijalkakäytävä olisi, jos sen leveys on 2,0 metriä. Maan säde päiväntasaajalla on 6 378 kilometriä.

riippumaton Yksikkömuunnos on tehty oikein esimerkiksi kilometrien ja metrien välillä 6 378 km = 6 378 000 m TAI tilavuuksien välillä (voi käydä ilmi myös laskuista). Tämän rivin pisteisiin riittää, että ainakin yksi yksikönmuunnos on oikein koko tehtävässä. (1 p.)

Jalkakäytävän pituus on TAI maapallon piiri on TAI ratkaisusta käy ilmi, että lasketaan piiriä / 6378000\cdot 2\pi (=40074155\mathrm{,}8\ldots metriä). (1 + 2  p.)

riippumaton Muodostettu oikea yhtälö \textrm{tilavuus}=\textrm{piiri}\cdot 2\cdot h jalkakäytävän korkeuden h ratkaisemiseksi TAI jalkakäytävän korkeus on \frac{\textrm{tilavuus}}{\textrm{piiri}\cdot 2} TAI muu selitys jalkakäytävän korkeuden lausekkeelle. Tämän rivin pisteisiin riittää idea tai (oikeilla tai väärillä) luvuilla annettu yhtälö tai lauseke. (2 p.)

Jalkakäytävän korkeus on 3.000.000 /(6.378.000 *2 *~p *2) TAI tehty omien mielekkäiden lukujen sijoitus oikein korkeuden lausekkeeseen (tilavuus 1 p., piiri 1 p., leveys 1 p.). (3 p.)

Oikealla logiikalla tehdyn laskun tuloksen pyöristys yhden tai kahden merkitsevän numeron tarkkuuteen/oikea vastaus ~~0,037melko täsmälleen 4 TAI melko täsmälleen 3{,}7/yksikkö ilmoitettu ja linjassa omien laskujen kanssa. (1 p. + 1 p. + 1 p.)

Tähän tehtävään liittyvät erillisohjeet

Ratkaistu yhtälö kokeilemalla (1+3+2+2+2). (max 10 p.)

Virheelliset arvot piirille:
– 6{,}378{,}000\ \textrm{m} TAI 6{,}378{,}000\ \textrm{m}\cdot 2 (1+0+2+[1+0+1]+[0+0+1]) (max 6 p.)

– 6{,}378{,}000\ \textrm{m} halkaisijana (1+[1+1]+2+3+[1+0+1]) (max 10 p.)

Väärä tilavuus, esimerkiksi V=3\,000\,000\,000\ \textrm{m}^3 (1+3+2+2+2) (max 10 p.)

Tehtävän voi ratkaista myös ympyrälieriön tilavuuden avulla (max 12 p.)

Koska jalkakäytävä on oletettavasti hyvin matala, ei Maan kaarevuutta tarvitse huomioida.

4. Laskuja ja käsitteitä 12 p.

Valitse oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 1–2 p., väärä vastaus 0 p., ei vastausta 0 p. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, poista vastauksesi valitsemalla pudotusvalikosta tyhjä rivi.

4.1 Täydennä virke. 2 p.

  • 6  (2 p.)

4.2 Täydennä virke. 2 p.

  • 6  (2 p.)

4.3 Täydennä virke. 2 p.

  • 0,3  (2 p.)

4.4 Täydennä virke. 2 p.

4.4.1 1 p.

  • yhteenlaskusäännöllä  (1 p.)

4.4.2 1 p.

  • toisensa poissulkevia  (1 p.)

4.5 Täydennä virke. 2 p.

  • koron korko  (2 p.)

4.6 Täydennä virke. 2 p.

  • on yli 17 % suurempi  (2 p.)

5. Snooker 12 p.

Snooker-biljardipelin alkutilanteessa pöydälle asetetaan 15 punaista palloa. Ne järjestetään kolmion muotoiseksi ryhmäksi käyttämällä tasasivuisen kolmion muotoista kehystä, jonka avulla ryhmästä saadaan mahdollisimman tiivis (kuva alla). Mikä on kehyskolmion sisäosan sivun pituus? Yhden pallon halkaisija on 52,4 mm.

riippumaton Hahmotettu tilannetta keskiosan ja ylijäävien kulmien avulla (ideapiste). (1 p.)

riippumaton Löydetty 30-60-90 asteinen kolmio + pidemmän kateetin laskeminen esimerkiksi tangentin tai muistikolmion avulla (ideapisteet). (1+1 p.)

Yhdistetään kulmissa olevien pallojen keskipisteet kohtisuorasti sivuihin TAI muu selkeästi ilmaistu tapa jakaa kysytty pituus laskettavissa oleviin osiin. (2 p.)

STOP Seuraavat pisteet vain, jos edelliseltä riviltä 1 p. tai 2 p.:

Kohtisuorien leikkauspisteiden väliin jäävä pituus on 4\cdot 52{,}4=209{,}6 (mm). (2 p.)

ylläolevista riveistä riippumaton piste Yhteen kulmaan ylijäävä pituus on \frac{26\mathrm{,}2}{\tan(30^{\circ})} \approx 45\mathrm{,}3797 (mm).

(kaavan muodossa virhe -2 p., esimerkiksi tangentin sijaan sini) (4 p.)

Laskettu yhteen oma keskiosa ja kaksi kertaa kulmaosa (2–4 merkitsevää numeroa vastauksessa; 209{,}6 +2\cdot 45{,}3797= 300{,}36\ldots\approx 300 (mm) tai 30\mathrm{,}0\approx 30 cm). (1 p.)

Tähän tehtävään liittyvät erillisohjeet

Ei pisteitä pinta-alan, tilavuuden tai säteen laskemisesta. (+0 )

Alkupiste: 5\cdot 52{,}4 TAI 4\cdot 52\mathrm{,}4 TAI 6\cdot 52\mathrm{,}4. (1 p.)

Toiseksi viimeisellä rivillä laskimessa radiaanit, laskettu \tan(30) ja negatiivinen vastaus, riviltä max 2. (max 10 p.)

6. Hätäpuhelut 12 p.

Hätäkeskukseen soitettiin vuonna 2022 yhteensä 2 920 000 puhelua. Niistä 694 600 oli vahinkopuheluita ja 37 600 häiriköintiä tai muuten asiattomia puheluita. Kutsutaan näitä turhiksi hätäpuheluiksi.

  1. Kuinka monta turhaa hätäpuhelua tuli keskimäärin yhden tunnin aikana? (3 p.)
  2. Arvioi binomijakauman kaavaa käyttämällä, millä todennäköisyydellä kymmenestä satunnaisesti valitusta puhelusta korkeintaan yksi oli turha. (9 p.)

1.

Koska vuodessa on yhteensä 365\cdot24(=8\,760) tuntia (1 p.)

ja turhia hätäpuheluita soitettiin yhteensä 694\, 600+37\, 600(=732\,200) kappaletta, [1 p.]

on tunnissa tullut keskimäärin \frac{694\, 600+37\, 600}{365\cdot 24}\approx 84 (tai 80 tai 83\mathrm{,}6) turhaa puhelua. (1 p.)

Tähän osatehtävään liittyvät erillisohjeet

Tyyppivirhe \frac{694\, 600}{365\cdot 24}\approx 79 tai \frac{37\, 600}{365\cdot 24}\approx 4\mathrm{,}3. (max 2 p.)

2.

Puhelu on turha todennäköisyydellä (694.000 +37.600) /2.920.000 =732.300 /2.920.000 (~~0,25075). (2 p.)

Puhelu ei ole turha todennäköisyydellä 1 -732.2007 /2.920.000 =2.187.800 /2.920.000 (~~0,74925). (1 p.)

Tapaus ''korkeintaan yksi puhelu oli turha'' vastaa sitä, että on joko yksi turha puhelu tai ei yhtään turhaa puhelua. [1 p.]

Näiden yhteenlaskettu todennäköisyys on (2.187.800 /2.920.000)^10 +((10), (1)) *(2.187.800 /2.920.000)^9 *(732.200/2.920.000)
(ensimmäinen summattava 1 p., toisen summattavan kaksi tulontekijää kolmesta oikein 1 p., toinen summattava oikein 2 p.). (4 p.)

Mahdollisia laskuvirheitä lukuunottamatta oikeasta lausekkeesta saatu vastaus pyöristetty 2–4 merkitsevään numeroon (\approx 0\mathrm{,}242332\approx 24{,}2\,\%). (1 p.)

Tähän osatehtävään liittyvät erillisohjeet

Tehtävä ratkaistu ilman binomijakauman kaavaa, esimerkiksi \text{binompmf}(10;10;p)+\text{binompmf}(9;10;p)\approx 24. (2+1+1+1+1). (max 6 p.)

Binomikerroin puuttuu (2+1+1+2+0). (max 6 p.)

Tapaus ''ei yhtään turhaa'' puuttuu (2+1+0+3+0). (max 6 p.)

Ensimmäisestä kohdasta periytyvät väärät alkuarvot. (max 9 p.)

1–2 rivin pisteet edellyttävät, että laskut ovat näkyvissä. Ne voivat olla esimerkiksi osatehtävässä 6.1 tai neljännen rivin laskun yhteydessä.

Ohjelmistoratkaisuissa 2. osatehtävän toisen rivin pisteet saa automaattisesti, jos p on syötetty oikein ohjelmistoon (koska lukua 1-p ei tarvitse syöttää)

Binomijakauman muuttujia ei tarvitse selittää, kunhan luvut ilmestyvät oikeille paikoille kaavaan.

B-osa

7. Verrannollisuus 12 p.

  1. Suomalainen muuttoyritys otti vuonna 2022 käyttöön katolle sijoitetuilla aurinkopaneeleilla varustetun muuttoauton. Paneelit tuottavat virtaa muuttoauton muihin kuin etenemiseen tarvittaviin toimintoihin. Paneelit tuottavat yhteensä 2,7 kilowatin tehon, jos niiden pinta-ala on 20 m^2. Kuinka suuren tehon tuottaa rekka-auton katolle sijoitettu paneeli, jonka pinta-ala on 32 m^2 ? Paneelien teho on suoraan verrannollinen niiden pinta-alaan. (4 p.)
  2. Kirkasvalolampun valaistusvoimakkuus on 2 500 luksia 45 senttimetrin etäisyydellä. Kuinka suuri on valaistusvoimakkuus 1,0 metrin etäisyydellä? Valaistusvoimakkuus on kääntäen verrannollinen etäisyyden toiseen potenssiin. (8 p.)

1.

Paneelin teho 32 /20 *2,7 =4,32 ~~4,3 kW (oikea suhde, esimerkiksi \tfrac{32}{20} tai \tfrac{2,7}{20} 2 p. (vain 0 tai 2 p.), oikea tulo 1 p., vastaus 1 p.). (4 p.)

TAI

x /2,7 =32 /20, [2 p.]

josta x\approx2\mathrm{,}7\cdot \frac{32}{20}\approx 4\mathrm{,}3 kW. (2 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Pelkkä lasku 2,7 *(32 /20) ~~4,3 kW tms. (max 4 p.)

Pinta-alat neliöity \frac{x}{2\mathrm{,}7}=\frac{32^2}{20^2}\Rightarrow x\approx6{,}9 kW, (0+2). (max 2 p.)

2.

Yksikkömuunnos oikein (1 m =100 cm,). [1 p.]

Pituudet (100^2 ja 45^2) neliöity oikein. (1+1 p.)

Oikeantyyppinen kääntäenverrannollisuus, esimerkiksi \frac{2500}{100^2}=\frac{x}{45^2} tai \frac{2500}{x}=\frac{100^2}{45^2} tai 2500\cdot 45^2=100^2x (3 p.) TAI lauseke ja sen perustelu esimerkiksi \frac{2500\cdot 45^2}{100^2} ja taulukko (2 p.+ 1 p.). (3 p.)

Saatu x\approx 506\mathrm{,}25\approx\, melko täsmälleen 510 luksia (lasku + pyöristys ja yksikkö, ks. Huom1). (1+1 p.)

Tähän osatehtävään liittyvät erillisohjeet

Oikeantyyppinen verrantoyhtälö, pituuksien suhde neliöity \frac{2500}{x}=(\frac{100}{45})^2, -0 p. (max 8 p.)

Pelkkä lasku 2500\cdot 45^2/100^2\approx 510 luksia (1+2+2+2). (max 7 p.)

Neliöinti puuttuu, \frac{2500}{100}=\frac{x}{45}, tai neliön asemessa muu väärä potenssi (1+0+3+0). (max 4 p.)

Väärä verrannollisuus, esimerkiksi \frac{x}{45^2}=\frac{100^2}{2500} (1+2+0+0). (max 3 p.)

Tähän tehtävään liittyvät erillisohjeet

Huom1: Yksikkö puuttuu/väärin vastauksissa, koko tehtävässä -1 p.

Matemaattisten merkintöjen väärinkäyttö, esimerkiksi "20\, \mathrm{m}^2=2{,}7 kW" -1 p.

8. Lenkkeilevä sensori 12 p.

Matematiikan sensori haluaa selvittää juoksu- ja kävelyvauhtinsa. Hänellä on käytettävissään seuraavat tiedot:

23.11.2023: Yhteensä 31,7 min, josta juoksua 25,0 min ja loput kävelyä, kokonaismatka 4,05 km.

25.11.2023: Yhteensä 39,5 min, josta juoksua 28,0 min ja loput kävelyä, kokonaismatka 4,30 km.

Näiden kahden päivän välillä keli oli muuttunut hyvin liukkaaksi, joten sensori arveli jälkimmäisellä kerralla vauhtinsa olleen noin 7/8 edellisen lenkin vauhdista sekä kävely- että juoksuosuuksilla.

Määritä sensorin kävelyvauhti ja juoksuvauhti ensimmäisellä lenkillä yksikkönä km/h.

riippumaton Muuttujat esitelty jotenkin esimerkiksi j juoksunopeus ja k kävelynopeus. (1 p.)

Ensimmäisenä päivänä kuljetun matkan perusteella saadaan yhtälö 4,05 =25 j +(31,7 -25) k TAI 4{,}05=25j+6{,}7k.Pisteytysperiaate: kuljettuun matkaan viittaava selitys yhtälölle (1 p.), erotus 31\mathrm{,}7-25 TAI kävelyaika 6{,}7 (1 p.), yksi oikea ajan ja nopeusmuuttujan tulo (1 p.) ja loput termit oikein (1 p.). (4 p.)

Toisen päivän hitaamman vauhdin perusteella saadaan yhtälö 4\mathrm{,}3= 28 \cdot \frac{7}{8}j+(39\mathrm{,}5-28) \cdot \frac{7}{8} k TAI 4\mathrm{,}3= 28 \cdot \frac{7}{8} j+ 11\mathrm{,}5 \cdot \frac{7}{8}k. Pisteytysperiaate: ajan ja nopeusmuuttujien tulot (1+1 p.), tekijä \frac{7}{8} ainakin kerran oikein (1 p.), yhtälössä virhe max 2. (3 p.)

Dokumentaatio lineaarisen yhtälöparin ratkaisemisesta (näppäily- tai laskuvirheet -0 p., oikeat tulokset: j \approx 0{,}137 km/min, k \approx 0{,}095 km/min.) (1 p.)

riippumaton Yksikkömuunnos km/min\tokm/h oikein TAI muutettu vähintään kaksi tehtävän kannalta relevanttia aikaa tunneiksi. (1 p.)

Saadaan j\approx 8{,}19777\approx melko täsmälleen 8{,}2\,\text{km/h} ja k\approx5{,}67997 \approx melko täsmälleen 5{,}7\,\text{km/h} (vastaukset 1 p. + oikealla logiikalla saatujen vastausten pyöristys 1 p.). (1+1 p.)

Tähän tehtävään liittyvät erillisohjeet

Jos vain toinen päivä tutkittu, niin pisteytetään se toisen rivin mukaan.

Tyyppivirhe: Laskettu vain keskinopeus (0+0+0+0+1+0). (max 1 p.)

Tyyppivirhe: Laskettu juoksun ja kävelyn aikaosuudet, luultu samoiksi kuin matkaosuudet jolloin päädytään samoihin nopeuksiin (0+1+0+0+1+0). (max 2 p.)

9. Pianon osto 12 p.

Auri haluaa ostaa uuden pianon. Hän aikoo säästää 7500 euroa kolmessa vuodessa ja tallettaa uudelle säästötililleen saman summan jokaisen kuukauden ensimmäisenä päivänä ennen pankkipäivän alkua. Kuinka paljon Aurin on laitettava säästöön kuukausittain, kun hänen säästötilinsä nettokorkokanta on 2,5 % ja korko maksetaan tilille kerran vuodessa? Tehtävässä oletetaan, että kaikki kuukaudet ovat samanpituisia. Tilillä olevat rahat kerryttävät korkoa koko sen ajan, jonka ne ovat tilillä.

Ratkaisu yhtälöllä

Ratkaisusta ilmenee korkokerroin 1{,}025 ja kuukausikorko \frac{0{,}025}{12}\,(=0{,}00208333\ldots). (1+1 p.)

Kuukausitalletus on esitetty muuttujana, esimerkiksi "Olkoon kuukausitalletus x." (1 p.)

STOP Ilman muuttujaa tai yhtälöä arvostellaan jälkimmäisen arvosteluohjeen mukaan.

Ensimmäinen talletus kasvaa korkoa x *0,025 ensimmäisen vuoden aikana. [1 p.]

Ensimmäisen vuoden jälkeen on tilillä 12x+\frac{0\mathrm{,}025}{12}(1+2+\cdots +12)x. (3 p.)

Vastaavasti lasketaan myös toisen ja kolmannen vuoden aikana talletettujen rahamäärien vaikutus talletusvuonna (ymmärretty, että vuodet ovat samanlaisia + oikealla logiikalla laskettuihin vuosiin perustuva toteutus). (1+1 p.)

Oikea idea siitä, että korolle kertyy korkoa, [1 p.]

eli kolmen vuoden jälkeen tilillä on (12 x +(0,025 /12) *(1 +2 +... +12) x) (1,025^2 +1,025 +1). (1 p.)

Tilin saldon on oltava 7500. Ratkaistaan yhtälö ja saadaan talletuksen suuruudeksi 200\mathrm{,}50 euroa. (1 p.)

Tähän ratkaisuun liittyvät erillisohjeet

Tyyppivirhe: Laskettu vuositalletukseksi 2379{,}05 euroa ja jaettu se kuukausien lukumäärällä 12. Saatu vastaukseksi 198{,}25 euroa (1+0+1+0+1+1+0+0). (max 4 p.)

Huom! Edellisessä tyyppivirheessä vuositalletus voi näkyä ratkaisuissa muuttujana muodossa 12x. Jos ratkaisussa on todettu, että kuukausitalletus on x, niin annetaan myös 2. rivin piste. (max 5 p.)

Tyyppivirhe: Vain yksi talletus. Yksittäinen rahasumma kasvaa korkoa 3 vuotta. x \cdot 1{,}025^3 = 7500, joten x=6964{,}5, ja vastauksena 6964{,}5/36 = 193{,}46. (1+0+1+0+0+1+0+0) (max 3 p.)

TAI Ratkaisu taulukkolaskentaohjelmistolla tai eurolasku ja skaalaus

Ratkaisusta ilmenee korkokerroin 1{,}025. (1 p.)

Taulukosta käy ilmi (mahdollisesti implisiittisesti) ensimmäisen talletuksen korko ensimmäisen vuoden aikana. [1 p.]

Ensimmäinen vuosi on oikein ja oikeat komennot on dokumentoitu. (1+1 p.)

Taulukossa toisen ja kolmannen vuoden korot näkyvät ja ne ovat oikein. (2 p.)

Taulukosta käy ilmi korkoa korolle vaikutus ja oikeat komennot on dokumentoitu. (1+1 p.)

Kokonaisvaikutus on oikein tilin loppusaldon laskussa. (1 p.)

Talletuksen suuruudeksi on saatu 200\mathrm{,}50 euroa. (1 p.)

Ratkaisu sisältää tarpeelliset selitykset, joista nähdään, että tämä on ainoa ratkaisu. (2 p.)

Tähän tehtävään liittyvät erillisohjeet

Jos laskee korkoa korolle kuukausittain korkokertoimella arvostellaan ensimmäisessä skeemassa 2+1+0+0+1+1+0+0. Tämän voi tehdä myös ohjelmiston käskyllä. (max 5 p.)

Alkupiste: Vastauksena kuukausitalletus väliltä 198 − 203 euroa, jota on perusteltu laskemalla tai taulukoimalla. Huom! Tätä pistettä ei saa, jos menetelmä on sellainen, että tälle välille ei päätyisi paitsi pyöristysten seurauksena. (1 p.)

10. Funktioiden tulkinta 18 p.

Tarkastellaan kolmea eri funktiota, jotka on annettu seuraavan taulukon vasemmassa sarakkeessa.

Funktio Yhtälö
f(t) =6000 t +200.000 f(t) =300.000
g(t) =50.000 *(0,8)^t g(t) =5000
h(t) =2^(0,5 t) h(t) =1.048.576

Kaikille funktioille on yhteistä se, että muuttujana on aika (jonka yksikkönä voi olla esimerkiksi vuosi, kuukausi, vuorokausi, tunti tai sekunti).

  1. Tarkastele funktiota f. (6 p.)
    1. Esitä sanallisesti käytännön elämään liittyvä esimerkki, jota funktiolla voidaan mallintaa. Kerro myös, mitä funktiossa olevat luvut ja muuttuja tarkoittavat esimerkkisi tapauksessa.
    2. Arvioi mallin hyvyyttä ja käyttökelpoisuutta valitsemassasi esimerkissä.
    3. Ratkaise taulukon oikeassa sarakkeessa annettu yhtälö. Tulkitse sanallisesti, mitä esimerkissäsi tarkoittaa se, että funktio saa yhtälössä annetun arvon.
  2. Tarkastele funktiota g ja tee tehtävät i–iii, kuten funktion f tapauksessa edellä. (6 p.)
  3. Tarkastele funktiota h ja tee tehtävät i–iii, kuten funktion f tapauksessa edellä. (6 p.)

1.

Annettu konkreettinen esimerkki, jossa 6\,000 on ymmärretty muutokseksi tietyssä ajassa. [1 p.]

On uskottavaa, että annettu ilmiö noudattaa kasvavaa lineaarista mallia ja funktio f sopii ilmiöön. Selitetty yksikköineen 200\,000, 6\,000 ja t, missä t on aika. (1 p.)

riippumaton Jotenkin järkevän mallin hyvyyttä on arvioitu matemaattisesti perustellulla tavalla (1 p.) TAI uskottavan mallin hyvyyttä tai käyttökelpoisuutta arvioitu jonkin konkreettisen huomion kautta järkevästi (2 p., esimerkiksi arvioitu että kasvunopeus ei ole täysin vakio tai että kasvu ei voi jatkua loputtomiin). (2 p.)

riippumaton Yhtälöstä 6\,000t+200\,000 = 300\,000 ratkaistu t \approx 17. (1 p.)

riippumaton Selitetty, mitä tarkoittaa että f saa arvon 300\,000 ajanhetkellä t oman (mahdollisesti vääränlaisen) esimerkin tapauksessa. (1 p.)

2.

Annettu konkreettinen esimerkki, jossa 0{,}8 on ymmärretty tiettyä aikaa vastaavaksi muutoskertoimeksi tai ymmärretty, että suure vähenee 20\,\% tietyssä ajassa. [1 p.]

On uskottavaa, että annettu ilmiö noudattaa vähenevää eksponentiaalista mallia ja funktio g sopii ilmiöön. Selitetty 0{,}8 ja yksikköineen 50\,000 ja t, missä t on aika. (1 p.)

riippumaton Jotenkin järkevän mallin hyvyyttä on arvioitu matemaattisesti perustellulla tavalla (1 p.) TAI uskottavan mallin hyvyyttä tai käyttökelpoisuutta arvioitu jonkin konkreettisen huomion kautta järkevästi (2 p., esimerkiksi arvioitu että muutoskerroin ei ole täysin vakio tai että väheneminen ei voi jatkua loputtomiin). (2 p.)

riippumaton Yhtälöstä 50\,000\cdot 0\mathrm{,}8^t=5\,000 ratkaistu t\approx 10. (1 p.)

riippumaton Selitetty, mitä tarkoittaa että g saa arvon 5\,000 ajanhetkellä t oman (mahdollisesti vääränlaisen) esimerkin tapauksessa. (1 p.)

3.

Annettu konkreettinen esimerkki, jossa on ymmärretty suureen kaksinkertaistuvan tietyssä ajassa. [1 p.]

On uskottavaa, että annettu ilmiö noudattaa kasvavaa eksponentiaalista mallia ja funktio h sopii ilmiöön. Selitetty luvut 2 ja 0{,}5 sekä ajan t yksikkö. (1 p.)

riippumaton Jotenkin järkevän mallin hyvyyttä on arvioitu matemaattisesti perustellulla tavalla (1 p.) TAI uskottavan mallin hyvyyttä tai käyttökelpoisuutta arvioitu jonkin konkreettisen huomion kautta järkevästi (2 p., esimerkiksi arvioitu että muutoskerroin ei ole täysin vakio tai että kasvu ei voi jatkua loputtomiin). (2 p.)

riippumaton Yhtälöstä 2^(0,5 t) =1.048.576 ratkaisu t =40. (1 p.)

riippumaton Selitetty, mitä tarkoittaa että h saa arvon 1\,048\,576 ajanhetkellä t oman (mahdollisesti vääränlaisen) esimerkin tapauksessa. (1 p.)

Tähän osatehtävään liittyvät erillisohjeet

"Jos t on pariton, niin h(t) ei ole kokonaisluku, ja siksi malli ei ole hyvä." (+0 p.)

Tähän tehtävään liittyvät erillisohjeet

Joka osatehtävässä rivit 1, 4 ja 5 voi saada, vaikkei malli olisi lainkaan realistinen.

"Jotenkin järkevän mallin" voi tunnistaa siitä, että alkutilanne tai muutoksen suuruus on kohtuullinen tilanteeseen nähden. Esimerkiksi kaupungin väkiluku on 200000 on kohtuullinen, mutta ihmisen pituus on 200000 metriä ei ole.

Jos t ei ole aika: joka osatehtävässä max1 =(0+0+0+1+0).

Jos t:n yksikkö käy ilmi implisiittisesti, koko tehtävästä yhteensä -1 p. Jos yksilöt puuttuvat täysin, niin ei minkään osatehtävän rivin 2 pistettä.

Yhtälön ratkaisu oikein, mutta ei järkevässä muodossa (esim. osatehtävässä 10.2 tarkka arvo) -1 p. yhteensä neljänsiltä riveiltä.

Pohdittu missä yhteydessä funktiota voi käyttää. (+0 p.)

11. Polynomifunktio 18 p.

Valitse osatehtävissä 11.1–11.6 oikea vaihtoehto. Vastauksia ei tarvitse perustella. Oikea vastaus 1 p., väärä vastaus 0 p., ei vastausta 0 p. Vastattuasi väittämään voit vaihtaa vastausvaihtoehtoa, mutta et voi jättää väittämää enää kokonaan ilman vastausta. Jos olet aloittanut tehtävään vastaamisen, mutta et haluakaan jättää tehtävää arvosteltavaksi, merkitse jokaiseen väittämään vaihtoehto ”En vastaa”.

Vastaa osatehtävään 11.7 normaalisti perustellen.

11.1 Onko seuraava väittämä tosi vai epätosi? 1 p.

Polynomifunktion suurin arvo saavutetaan aina derivaatan nollakohdassa. 

  • Epätosi  (1 p.)

11.2 Onko seuraava väittämä tosi vai epätosi? 1 p.

  • Tosi  (1 p.)

11.3 Onko seuraava väittämä tosi vai epätosi? 1 p.

  • Tosi  (1 p.)

11.4 Onko seuraava väittämä tosi vai epätosi? 1 p.

  • Epätosi  (1 p.)

11.5 Onko seuraava väittämä tosi vai epätosi? 1 p.

  • Epätosi  (1 p.)

11.6 Onko seuraava väittämä tosi vai epätosi? 1 p.

  • Epätosi  (1 p.)

11.7 Vastaa osatehtävään 11.7 normaalisti perustellen. 12 p.

  1. Laskettu f(1)=8 ja f(3)=24 TAI f(3)-f(1)=16. (1 p.)

    (f(3) -f(1)) /(3 -1) =(24 -8) /2 =8 (idea erotusosamäärästä + oma erotusosamäärä sievennetty (1+1 p.)

    TAI (ohjelmisto)

    Laskettu f(1)=8 ja f(3)=24 TAI koordinaatit (1, 8) ja (3, 24) näkyvissä. (1 p.)

    Perusteltu, että pisteiden kautta kulkeva suora on y=8x (käskyt näkyvissä). (1 p.)

    Keskimääräinen muutosnopeus on suoran kulmakerroin 8. (1 p.)

    Tähän osatehtävään liittyvät erillisohjeet

    Laskettu funktion arvojen keskiarvo \frac{f(1) +f(3)}{2} =\frac{8+24}{2} =16. (1+0+0 p.)
    Laskettu derivaatan arvojen keskiarvo \frac{f'(1) +f'(3)}{2} =\frac{-10 +58}{2} =24. (0 p.)

  2. f'(x) =4 x^3 -18 x +4 (2 termiä oikein (saa olla ylimääräisiä) + kokonaan oikein). (1+1 p.)

    Nollakohdat ovat melko täsmälleen x =2, melko täsmälleen x =\frac{-2+\sqrt{6}}{2} \,(\approx 0{,}22) ja melko täsmälleen x =\frac{-2-\sqrt{6}}{2} \,(\approx -2{,}22). (1 p.)

    Tähän osatehtävään liittyvät erillisohjeet

    Nollakohdat koordinaatteina, esimerkiksi (2,0). (max 3 p.)

    Nollakohdat vain likiarvoina TAI laskinratkaisussa ei komentoa näkyvissä (2+0). (max 2 p.)

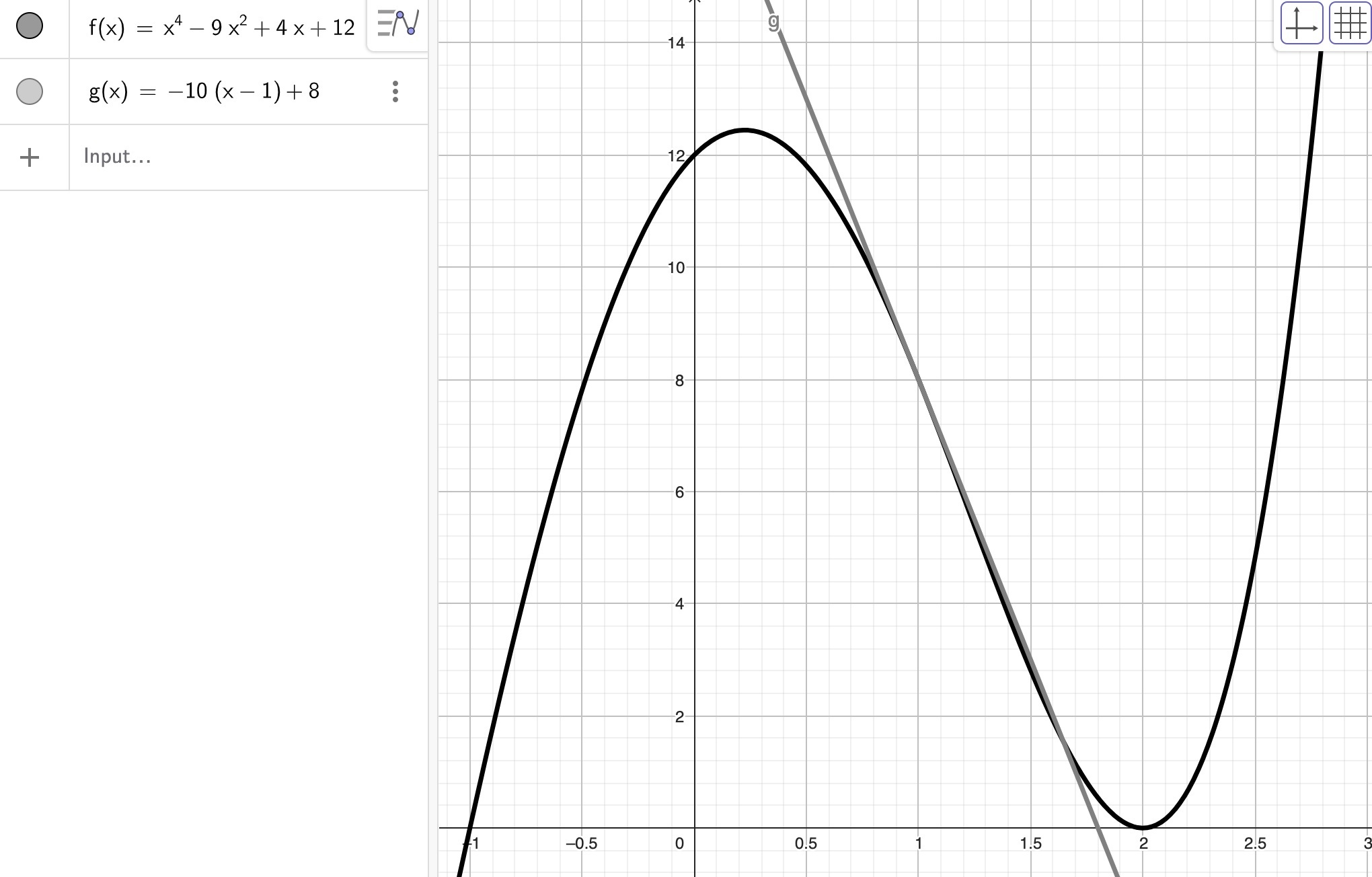
  3. Piirretty kohdan x=1 sisältävällä välillä kuva, jossa on silmämääräisesti oikea funktio ja silmämääräisesti oikea tangentti. Kuvassa tulee näkyä tangentin ja funktion sivuamiskohta. (esimerkki alla). (1 p.)

    Oikein perusteltu tangentti y -8 =-10 (x -1) TAI y =-10 x + 18.

    (Esimerkki perustelusta: Koska f'(1) =-10 ja f(1) =8, on tangentin yhtälö y -8 =-10 (x -1) TAI Komento ja oikea tangentin yhtälö näkyvissä.) (1 p.)

    Hetkellinen muutosnopeus on -10, koska f'(1) =-10 TAI todettu että se on tangentin kulmakerroin. (1 p.)

    Tähän osatehtävään liittyvät erillisohjeet

    Tehty kohta väärällä funktiolla (esim. vakiotermi puuttuu tai käytetty funktiona derivaattafunktiota) oikein. (max 2 p.)

  4. Laskettu oman derivaatan, joka on kolmannen asteen polynomi, arvo yhden järkevän tarkasteluvälin sisäpisteessä ja todettu sen merkki.

    (Oikeat tarkasteluvälit: (-\infty, -1 -\sqrt{3/2}], [-1 -\sqrt{3/2}, \sqrt{3/2} -1], [\sqrt{3/2} -1, 2] ja [2, \infty).) (1 p.)

    Tehty sama muille järkeville tarkasteluväleille TAI todettu, että koska nollakohtia on kolme, ei kaksinkertaisia nollakohtia ole, joten derivaatta vaihtaa merkkiään nollakohdissa. (1 p.)

    Johtopäätöksenä: Funktio on kasvava väleillä [2, \infty) ja [-1 -\sqrt{3/2}, \sqrt{3/2} -1]. (1 p.)

    Tähän osatehtävään liittyvät erillisohjeet

    Tarkasteluvälin päätepisteistä vain likiarvot: pistemenetys vain ii osatehtävässä. (max 3 p.)

    Avoimet välit käyvät. (max 3 p.)

    Ratkaistu ohjelmistolla epäyhtälö f'(x)>0 ja tehty johtopäätös. (max 3 p.)

    (Muulla tavalla) perusteltu kulkukaavio ja vastaus. (max 3 p.)

    Esimerkki: Välin [2, \infty) testipiste: f'(3) =58 > 0. Välin [\sqrt{3/2} -1, 2] testipiste: f'(1) =-10 < 0. Välin [-1 -\sqrt{3/2}, \sqrt{3/2} -1] testipiste: f'(0) =4 > 0. Välin (-\infty, -1 -\sqrt{3/2}] testipiste: f'(-3) =-50.

    Katsottu vastaus kuvasta TAI perustelematon kulkukaavio. (0 p.)